“对数函数”教学中必须厘清的几个问题

广东省东莞市教研室　(523000)

易文辉



“对数函数”教学中必须厘清的几个问题

广东省东莞市教研室(523000)

易文辉

“对数函数”是高中数学函数内容的重点之一，是高中数学以“函数”与“运算”为主线的直接体现，是解决实际问题的一个重要函数模型，有非常广泛的实际应用背景；对数运算及对数函数的相关问题也是联系初等数学和高等数学的一个重要纽带，在历年的高考试题中，以对数函数为命题背景，结合高数知识、初等数学的最新研究成果的探究性试题在全国各地高考试卷中累见不鲜.

“对数函数”的内容在人教A版教材必修1第二章第2节，是高一学生学习的难点之一，对于对数的概念、运算及其图像性质即使到了高三，许多同学依然难于理解，其根源在高一学习时就遗留了许多问题，“对数函数”的学习是培养高一学生学习数学兴趣及其思维能力的一个重要载体，其教学的质量也是教师专业素养的直接体现，笔者认为要提高“对数函数”的教学效果，必须要厘清几个问题.

1　厘清“对数”的来源

1.1让概念的引入更加合理和自然

数学课堂应该对本原性问题多一些思考，围绕它来确立数学探究活动[1]，这里的本原性问题是指符合学生认知特点、科学的、能够体现知识的来源即本质的问题，主要有实际问题和数学内部的问题.而在教材中对数和对数函数的概念引入中，背景问题与知识概念产生没有“必要”联系，有些牵强(许多人称之为伪问题)，概念的给出也是比较“唐突”的，这里有许多内容需要老师进行二次开发.

1.2让数学名称的来历有根有据

孙维刚说:"科学上的任何规定都有为什么，数学尤其如此，世界上没有没有为什么的事."[2].然而实际教学中，很多学生问到数学名称怎么来的时候，老师就用“这是规定，没有为什么”来敷衍学生；其实，了解数学名称的来历，不仅有助于学生理解数学本质，也有利于提高学生学习的兴趣.在“对数”的学习过程中，有必要让学生了解相关名称的来历，以帮助学生理解知识的本质，比如为什么叫“真数”、“对数”？据考究，“对数”和“真数”的名词跟纳皮尔没有什么关系，对数于康熙年间传入中国，那时候对数的作用主要是将乘除运算化为加减运算，在整个运用对数进行计算的过程中，只有真数部分才是我们“真正计算的数”所以叫真数，而对数值只是起到一个桥梁的作用，所以对数最初叫“假数”，后来有了“真数和假数对列成表，故称对数表”，往后“对数”这个词越加深入人心，后来干脆称假数为对数[3].有些问题，也可以准备一些数学史相关的资料留给学生课后阅读，增加对知识来源的了解，以便更加准确地把握内容.

2　厘清研究问题的共性思维

很多时候，学生“会不会学”与老师“会不会教”是直接相关的，数学学习不是机械的模仿和训练，重要的是要能够基于理解的视角进行学习，也就是我们常说的“悟”——悟法、悟道，这种“悟”也不是什么“玄学”，而是体现在学习过程中的每一个环节，就看教师有没有“法眼”，能够揭示研究数学问题的共性思维，教给学生不仅仅是知识，而是思维、方法，研究数学问题的一般思路，也就是一种悟道的方法.

2.1让学生体验数学中研究新对象的一般思路

数学是思维的学科，只有在教学中揭示研究数学对象的基本方法，并提供机会让学生进行反思总结，才能真正培养学生理性思维能力.对数是学生进入高中以来所遇到的第二个新对象(第一个是集合)，是一次让学生体验研究数学对象基本思路的良好时机，因此有必要经历“背景(现实、数学内部)——定义——表示——分类——性质——运算——联系和应用”的研究思路进行教学设计，并让学生进行总结、反思，也只有站在“研究问题”的角度，才能更加好理解教材、使用教材，明晰教材内容编排的整体结构，有助于学生形成良好的学习习惯和思维能力.

2.2让学生体验数学中研究函数性质的一般思路

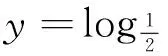
3　加强数学思想方法的渗透

又如，对数运算性质教学中，由MN=am+n得到loga(M·N)=m+n，即loga(M·N)=logaM+logaN既可以看作是对数定义的应用，也体现了“对数运算”的本质，将“乘法”化为“加法”，学习了函数之后，再从对数函数的性质的角度加以认识，就是f(MN)=f(M)+f(N)，这样揭示运算的思想和函数思想去理解对数的运算性质，对学生理解知识本质是非常有帮助的.

4　对教材编写的建议

在目前人教A版的教材中对知识、例题的处理，基本上都是“问题+解答”的模式，缺乏对问题的分析、总结反思、提炼，或者是部分具有代表性的问题，缺少了解决问题关键步骤的分析，对解决问题的示范效果打折扣.

4.1增加问题的分析与反思

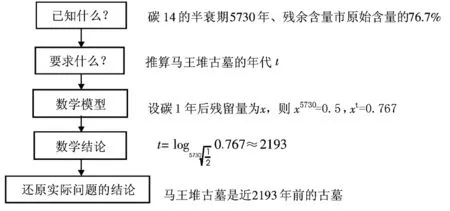
教材例题本来就具基础性、典型性和示范性的特征，这种典型，除了问题的代表性之外，解决问题的方法应该也具有典型示范的功能才是，所以对于部分例题，如果能够增加一些分析性文字，解题后对解决问题的共性思维有总结提炼的话，对指导学生学习，养成良好的思维习惯会有很好的帮助.例如，在教材(人教A版必修1第72页)“对数函数及其性质”中例8：“比较下列各组数中两个值的大小：(1)log23.4,log28.5……”，建议教材增加“分析：比较两个数的大小除了将两个值计算出来再比较以外，往往可以转化为两个函数值的大小比较或者两个函数图像的位置关系，解决这类问题首先要将问题转化为函数的语言进行描述，然后利用函数的图像性质去解决.”进而解题过程可以这样处理：log23.4,log28.5两个对数值的底数相同，因此它们是函数f(x)=log2x自变量分别取x1=3.4,x2=8.5的两个函数值，因为函数f(x)=log2x在(0,+∞)上是增函数，故f(3.4)

4.2呈现解决问题的步骤

根据例题的示范性功能，例题既是如何运用知识解题的典范也是思维训练的典范，既是常规数学思维方法的典范又是如何解题思维的典范，即示范性主要体现在知识运用、数学方法和数学思维示范三个层面，因此建议教材要重视通过例题来揭示数学思维，呈现解题步骤来示范效果，对数在实际问题中的应用，教材P66例5和例6处理中，就可以增加“用数学模型解决实际问题”的基本步骤：

这样左边以流程图的方式说明解决问题的思路，右边是具体问题的解决过程操作步骤，这样既直

观明了，揭示分析问题、解决问题的基本思路和方法，揭示本质，又具有可操作性和思维示范作用.

[1]花奎.围绕数学课堂教学中的本原性问题开展探究活动[J].中学数学研究(广州)，2015,11.

[2]孙维刚.孙维刚谈立志成才[M].北京：北京大学出版社，2006,8.

[3]郭龙先，刘秀.开辟大数计算新纪元——对数函数思想方法解析[J].昭通学院学报，2014,10.

[4]罗增儒.数学解题学引论[M].西安：陕西师范大学出版社，1997.

[5]陈永明工作室.数学习题教学研究[M].上海：上海教育出版社，2010,5.