暴露思维过程案例分析——例谈数学归纳法的应用

江苏省响水中学　(224600)

魏立国



暴露思维过程案例分析
——例谈数学归纳法的应用

江苏省响水中学(224600)

魏立国

数学归纳法应用广泛,可以说从代数到几何，从组合到数论，都能找到它的影子.如果使用恰当，往往能使陈题新解，难题巧解.本文试图通过暴露思维过程案例分析，和同行分享数学归纳法的妙用.

一、正确理解假设“n=k ”成立的含义，寻找通向“pk+1 ”的桥梁

案例2设n 是个不小于2的正整数，正整数a1，a2，…，an和为偶数，对任意1≤k≤n,k∈N*都有ak≤k, 求证：可适当地选择“+”或“- ”号使±a1±a2±…±an=0.

分析：①n=2 ，由a1≤1,a2≤2,a1,a2∈N*,a1+a2为偶数，则a1=a2=1,a1-a2=0 即证.

②假设n=m 成立，当n=m+1 时，ak≤k,可知，只有am+1可能为m+1,其余ai≤m(i≤m)，应用归纳假设必须把m+1 个数改造成m个数，和为偶数且最大不超过m.不妨令a1≤a2≤…≤am+1, 由ak≤k,ak∈N*，得a1=1 ，且am≥1,a1，a2，…，am-1不变，(am+1-am) 作为第m 个数，则am+1-am≤m, 由a1，a2，…，am+1加减不改变奇偶性，所以a1+a2+…am-1+(am+1-am) 为偶数.a1，a2，…，am-1，(am+1-am)这m 个数符合归纳假设条件.则存在一种选择使a1±a2±…am-1±(am+1-am)=0,即证n=m+1成立.

评注：要正确理解归纳假设“n=k” 成立的含义.否则，可能将成为伪证.

二、从特殊到一般

案例3乒乓球队有n个队员，在一次双打集训中，任意两名队员作为队友，恰好只搭档过一次双打比赛，求n所有可能值，并给每一个值给出一种比赛方案.(2012年华约自主招生试题)

分析：设Ai表示第i 个人.

(1)从最特殊的4人开始，不妨令4个人分别为A1、A2、A3、A4.则A1A2↔A3A4,A1A3↔A2A4,A1A4↔A2A3即可；

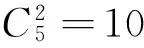
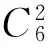
由此推断n=4k、4k+1 可能符合.

(2)下面对n=4k+1 时用数学归纳法进行证明.

①k=1 显然.

②假设n=4k+1 成立.当n=4k+5 时，由归纳假设A1，A2，…，A4K+1两两可以搭档双打一次.A4k+2、A4k+3、A4k+4、A4k+5这5个人， 由前面(1)中的讨论可知也可以两两双打一次.剩下的就是A4k+2、A4k+3、A4k+4、A4k+5与A1、A1…A4K+1没有两两搭档双打一次.很自然想到A4K+2Ai(i=1,2,…，4k+1) ↔A4K+3A4k+2-i,A4K+4Ai(i=1,2,…,4k+1)↔ A4K+5A4k+2-i.

如果搭档成功，问题就解决了.但是，当i=2k+1 时，Ai=A4K+2-i，这样就无法搭档.如果取Ai与A4k+1-i相对应.这样，i与4k+1-i不可能相等.因为，i与4k+1-i是一奇一偶.A4K+2Ai(i=1,2,…4k)↔A4K+3A4k+1-i,A4K+4Ai(i=1,2,…4k)↔A4K+5A4k+1-i，但是，这样A4K+1与A4k+2、A4k+3、A4k+4、A4k+5又没有两两搭档双打一次.由(1)可知n=5 可以两两搭档双打一次.所以，n=4k+5成立.

(3)同理，n=4k 也成立.

案例4(1)正六边形被3条互不交叉(端点可以重合)的对角线分割成4个三角形．将每个三角形区域涂上红、蓝两种颜色之一，使得有公共边的三角形涂的颜色不同．怎样分割并涂色可以使红色三角形个数与蓝色三角形个数的差最大？

(2)凸2016边形被2013条互不交叉(端点可以重合)的对角线分割成2014个三角形．将每个三角形区域涂上红、蓝两种颜色之一，使得有公共边的三角形涂的颜色不同．在上述分割并涂色的所有情形中，红色三角形个数与蓝色三角形个数之差的最大值是多少？证明你的结论．

(江苏省2014年高中数学竞赛初赛压轴题)

人们对竞赛题常常望而生畏，认为竞赛压轴题不是常人能做的.看了命题者提供的解答也确实如此.其实，本题如果把它推广到一般情况，利用数学归纳法普通人也能做.

图1

分析：(1)作如图1构造即可.

(2)2016是6的倍数，况且又是2014年竞赛题，是不是可以推广到一般情况呢？由此，我们可以猜想，是不是任意6k 边形，都可以涂为红比蓝多2k.我们不妨用数学归纳法试一试.

令红三角形有x个，蓝三角形有y个.因为在多边形内红三角形和蓝三角形是相邻的，所以，它们拥有相同多条对角线.只有多边形边它们不是公共边.所以，3x-3y≤2016,∴x-y≤672.所以，最大值为672.下面用数学归纳法证明：

①k=1 ，由(1)显然.(2)假设k=m 成立，如图2，根据归纳假设把A1A2…A6m边形涂好.如果A1A2…A6m边形中紧靠A1A6m边涂红，由(1)构造给我们启发，能否对剩下的八边形A1A6mA6m+1A6m+2A6m+3A6m+4A6m+5A6m+6先分割一个六边形，保持六边形中3红一蓝.连A6m+5A6m，按图2涂色，即可完成n=m 到n=m+1的过渡.同理，如果A1A2…A6m边形中紧靠A1A6m边涂蓝，按图3涂色，即可完成n=m 到n=m+1的过渡.

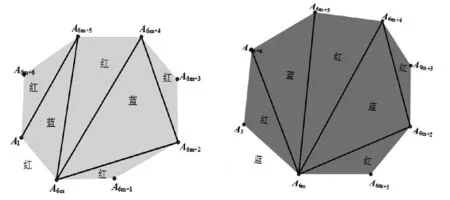
图2　　　　　　　　　　　　　图3

评注：(1)案例3通过4人、5人、6人、7人、猜想到了一般双打规律.案例4是通过数字特征把特殊推广到一般.

(2)案例4中的特殊情况证明对n=k 到n=k+1 的过渡起了关键性的作用.

三、增多起点，加大跨度

增多起点，加大跨度的实质就是通过验证①n=1，2，…，m步成立，②假设n=k,k+1,…，k+m-1 步成立，去推证n=k+m 成立.把原来一步跨度变为m 步跨度.

案例5f(n) 是定义在n∈N*的增函数，f(4)=5.①∀m,n∈N*,f(n)∈Z;②f(m)f(n)=f(mn)+f(m+n-1).

(1)求f(1),f(2),f(3);

(2)求f(n).

分析：(1)易得f(1)=2,f(2)=3,f(3)=4.

(2)由(1)易猜测f(n)=n+1 ，抽象函数必须恰当的赋值，获得f(k)、f(k+1).可令m=k,n=2，即得f(k)f(2)=f(2k)+f(k+1) ①.但是①中又出现了2k，此时， 可以考虑增多起点，加大跨度.

验证n=1,2成立.假设n=k,k+1成立,可得f(2k)=2k+1.但并没有得到f(k+2)=k+3,由于f(n)增函数，f(k)与f(2k)之间只有k个整数.f(k)=k+1,f(2k)=2k+1,所以，f(k+2)=k+3得证.看上去天衣无缝，没有问题，实际上是有问题的.问题出在哪里？因为得到这一结论，必须2k≥k+2,即k≥2,起步要从2,3开始验证.

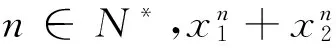
评注：从案例5、6看出，一方面增加跨度可降低归纳法证明的难度，另一方面让一个跨度不能证明的问题获得解决.

四、加强命题

评注：命题加强的度要把握恰当，否则，数学归纳法也无法奏效.

总之，数学归纳法以其特有的魅力，往往在高考、自主招生考试的压轴题中扮演着重要的角色，如果学生能适时恰当的使用数学归纳法，它往往会给普通学生增分添彩.