关于“反比例函数的图象和性质”一课的点评

刘志凤（河南省基础教育教学研究室）



关于“反比例函数的图象和性质”一课的点评

刘志凤（河南省基础教育教学研究室）

摘要：通过观摩“反比例函数的图象和性质”展示课，从对教材内容的理解、数学思想方法的渗透、多媒体技术的合理利用等方面概括了本节课的突出亮点，同时指出了本节课值得商榷和改进的地方.

关键词：反比例函数；图象和性质；数学思想方法；学生主体性

河南师范大学附属中学李婷老师的“反比例函数的图象和性质”一课在准确把握《义务教育数学课程标准（2011年版）》要求，正确解析教材内容，充分了解学生的认知水平与活动经验的基础上，环环相扣的教学环节设计，使本节课显得自然流畅，“数学味儿”浓.

一、亮点透视

1.关注数学的通性、通法

数学教学不但是让学生学会具体的数学知识，更重要的是通过一次次具体的探究过程，在理解与掌握一个个知识点的同时，获得研究数学问题的一般方法.李婷老师在本节课中就充分关注了研究函数问题的一般方法与基本套路，由函数解析式，到用描点法画出函数图象，再通过观察、分析、归纳、概括，得到函数性质，在这一探究过程中，反复引导学生进行解析式与函数性质间的数形转化分析与推理验证，有效地促进了学生对函数本质的理解.

2.关注数学思想方法的渗透教学

数学思想方法蕴含在数学知识形成、发展和应用的过程中，是数学知识和方法更高层次上的抽象与概括，教师应引导学生在积极参与数学活动中，通过独立思考、合作交流，逐步感悟而得到.显然李婷老师充分认识到了数学思想方法获得的特点与途径，在课堂教学中，设计了“一明一暗”两条主线来进行数学思想方法的渗透.“明线”有欣赏华罗庚先生的关于“数形结合”的一首词作为情境导入；对k＞0，k＜0的分类讨论、类比探究等数学思想方法的直接应用.“暗线”由解析式与图象及性质间的多次交互分析，引导学生充分体验、体会由“数”到“形”再由“形”到“数”的转化过程，深刻理解数形结合的分析、解决问题的思想方法；通过对几个具体的反比例函数图象的归纳、概括，得出y=的性质，再通过利用函数性质解决具体问题，并探究得出k互为相反数时两个函数图象间的关系，使学生充分体验了从特殊到一般，由一般到特殊的分析、研究问题的方法；通过回顾正比例函数，从学生最近的认知区域着手，引导学生类比探究等，精心的教学设计起到了润物细无声的作用，使数学思想方法的渗透教学水到渠成.

3.恰当运用多媒体辅助教学

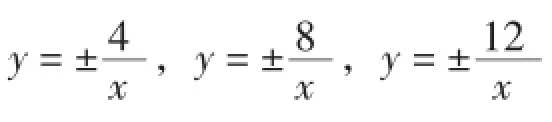
二、教学建议

在学生作品展示环节，教师如果有选择地展示课堂上学生的作图能力，充分利用课堂生成资源，效果应会更好一些.

教师可以放手更充分些，学生已经学习了一次函数、二次函数的图象和性质，有了研究函数问题的一些方法与经验，本节课可以把“在学习了反比例函数的意义后，下一步我们该从哪些方面对这类函数做进一步研究”这一问题抛给学生，引导学生主动类比已有研究函数的经验，自主提出本节课要研究的问题及研究方法，使学生的主体地位得到更好的落实.

参考文献：

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.

［3］陈德前.强化概念引领探索渗透方法：苏科版“2.7有理数的乘方（第1课时）”课堂实录与点评［J］.中国数学教育（初中版），2014（7/8）：47-53.

［4］董林伟.初中数学实验教学的理论与实践［M］.南京：江苏科学技术出版社，2013.

［5］刘金英，李庆.反比例函数的图象和性质（第一课时）教学设计与反思［J］.中国数学教育（初中版），2011（1/2）：26-29.

［6］魏晓丽，王冰.“等腰三角形的性质”教学设计及点评［J］.中国数学教育（初中版），2013（7/8）：36-38.

收稿日期：2015—12—10

作者简介：刘志凤（1967—），女，中学高级教师，教研员，主要从事中学数学教育教学研究.