“直角三角形外接圆截直角平分线”数学模型探究

王云峰（江苏省盐城市葛武初级中学）



“直角三角形外接圆截直角平分线”数学模型探究

王云峰（江苏省盐城市葛武初级中学）

摘要：解数学题的关键是寻找解题思路.从熟悉的数学模型入手是寻找解题思路的一种方法，教师要注意归纳、总结出一些数学模型．“直角三角形外接圆截直角平分线”数学模型在近几年中考试题中频频出现，通过对模型构建、模型变式、模型拓展、模型一般化进行解法探析，为教师的解题教学提供启示，以使学生达到融会贯通的境界．

关键词：角平分线；数学模型；中考应用

数学教育家波利亚曾说过，假如你想从解题中得到最大的收获，你就应当在所做的题目中去找出它的特征，那些特征在你以后求解其他问题时，能起到指引的作用．现介绍“直角三角形外接圆截直角平分线”模型及其变式、拓展、一般化等在解题中的应用，供大家参考．

一、模型构建

题目如图1，⊙O是Rt△ABC的外接圆，CD平分直角∠ACB交⊙O于点D，试探究线段AC，BC，CD之间的等量关系.

此题解法丰富多彩，限于篇幅，这里仅从变换的角度给出两种典型解法．

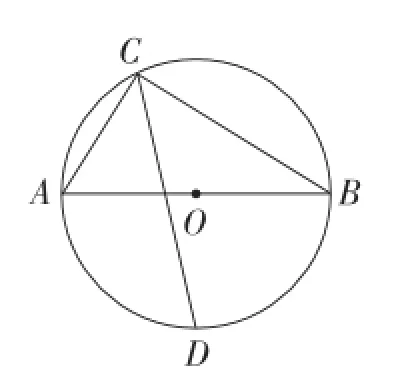
图1

思路1：利用轴对称变换，构造全等三角形.

解：（方法1）如图2，过点D作DE⊥CA，交CA的延长线于点E，作DF⊥BC于点F，连接AD，BD.

因为∠ACB=∠E=∠CFD＝90°，

所以四边形CEDF是矩形.

又由CD平分∠ACB，DE⊥CA，DF⊥BC，

得DE=DF.

所以四边形CEDF是正方形.

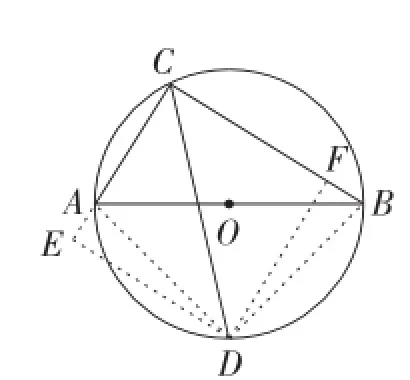
图2

因为∠ACD=∠BCD，

于是A（D=B（D.

所以AD=BD.

又因为DE=DF，

所以Rt△ADE≌Rt△BDF.

于是AE=BF.

【评析】遇到角平分线，常利用轴对称变换构造全等三角形．

思路2：利用旋转变换，构造全等三角形.

解：（方法2）如图3，连接AD，BD.

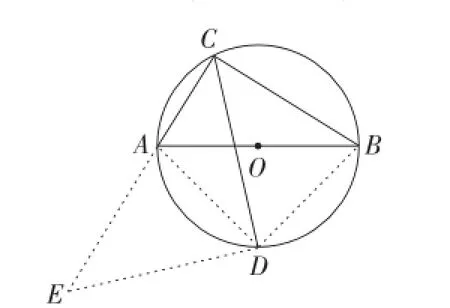
图3

因为∠ACD=∠BCD，

所以AD=BD，且∠ADB=90°.

将△BCD绕点D逆时针方向旋转90°到△AED处（点B，C分别落在点A，E处），

则∠EAD=∠CBD，AE=BC.

在四边形ACBD中，

∠CAD+∠CBD=360°-∠ACB-∠ADB=180°.

所以∠CAD+∠EAD=180°.

所以点C，A，E在一条直线上.

易知△CDE是等腰直角三角形.

【评析】遇到等腰直角三角形，常利用旋转变换构造全等三角形.

可见，⊙O截其内接Rt△ABC的直角平分线所得线段CD与直角边AC，BC之间存在等量关系AC+BC=CD，我们称之为“直角三角形外接圆截直角平分线”模型，即直角三角形两直角边的和等于该直角三角形的外接圆截直角平分线所得线段的倍.

例1 如图4，⊙O的直径AB的长为10，弦AC长为6，∠ACB的平分线交⊙O于点D，则CD长为（）.

（A）7

（D）9

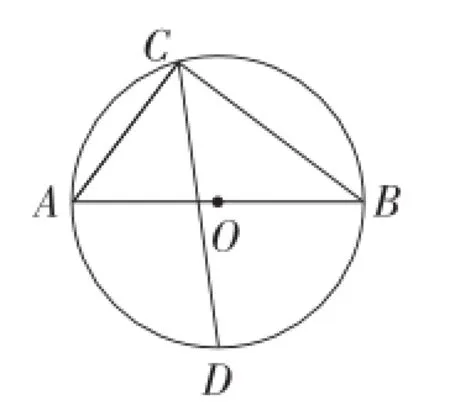
图4

解：因为AB是⊙O的直径，

所以∠ACB=90°.

因为CD平分直角∠ACB，

故选择选项B.

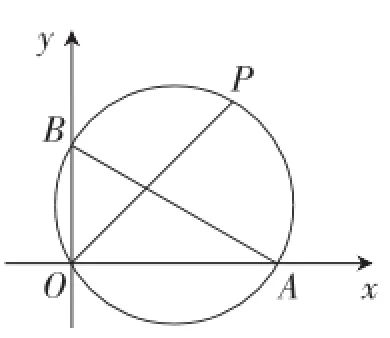
图5

图6

解：由∠AOP=45°可知，OP平分直角∠AOB.

如图6，过点P作PC⊥OA于点C，

二、模型变式

在图1中，若连接AD，BD，而点D在⊙O上，则∠ADB=90°.又由CD平分直角∠ACB，则AD= BD，于是可将⊙O进行隐身.

如图7，在四边形ACBD中，∠ACB=∠ADB=90°，AD=BD，则AC+BC=CD.

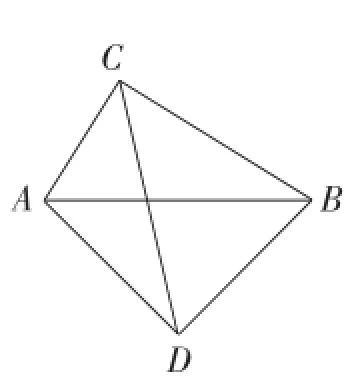
图7

可见，“直角三角形外接圆截直角平分线”模型可变身为特殊四边形，即一组对角是直角，且其中一直角的两边相等的四边形.如图7，四边形ACBD可看成是由等腰Rt△ABD与Rt△ABC（非等腰直角三角形）组合而成，此时结论AC+BC=CD用文字可表述为，直角三角形（非等腰直角三角形）的两直角边之和等于两直角顶点所连线段的倍.另外，由模型的解法2可知，图7中四边形ACBD可转化为以CD为腰的等腰直角三角形，因此S四边形ACBD=CD2，即面积等于两直角顶点所连线段的平方的一半（证明过程略）.

例3 如图8，在Rt△ABC中，∠ACB=90°，以斜边AB为边向外作正方形ABDE，且正方形对角线交于点O，连接OC，已知AC=5，OC=6，则另一直角边BC的长为＿＿＿＿＿＿.

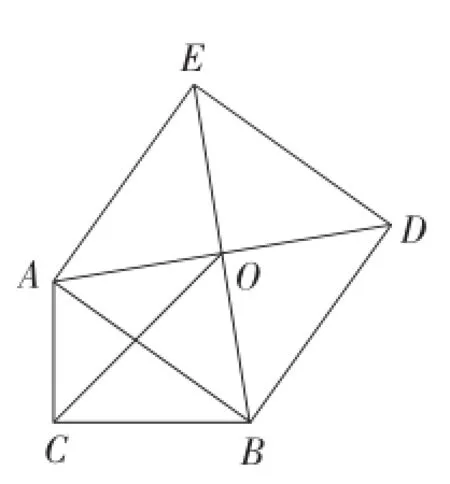
图8

解：由已知，易得∠AOB=∠ACB=90°，OA=OB.

解得BC=7.

例4 如图9，在四边形ABCD中，∠BAD=∠BCD=90°，AB=AD，若四边形ABCD的面积是24 cm2，则AC的长是＿＿＿＿＿＿＿＿.

解：因为∠BAD=∠BCD=90°，AB=AD，

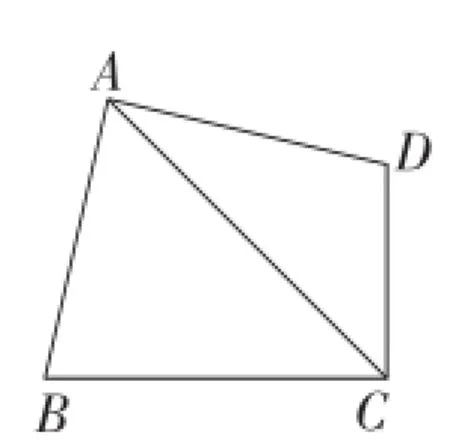
图9

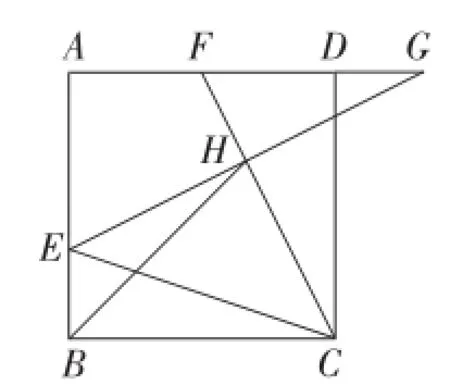
图10

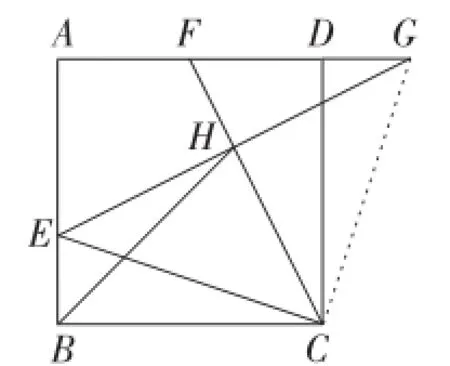
图11

解：如图11，连接CG.

因为BE=DG，∠EBC=∠GDC=90°，BC=DC，

所以△BCE≌△DCG.

于是∠BCE=∠DCG，EC=GC.

又因为CF⊥EG，

所以点H为EG的中点.

又因为∠ECG=∠ECD+∠DCG=∠ECD+∠BCE= ∠BCD=90°，

所以CH=EH.

在四边形BCHE中，∠EBC=∠EHC=90°，CH=EH，

易证△GFH∽△GEA.

三、模型拓展

在图1中连接AD，BD，则有AD=BD，若点C运动到半圆ADB上时（点C与点D不重合），此时线段AC，BC，CD之间又有怎样的等量关系呢？

当点C在B（D上时，如图12所示，将△BCD绕点D逆时针旋转90°到△AED处（点B，C分别落在点A，E处），

则AE=BC，DE=DC.

因为∠DAC=∠DBC，

所以点E在AC上.

于是有AC-BC=AC-AE=EC.

易知△CDE是等腰直角三角形.

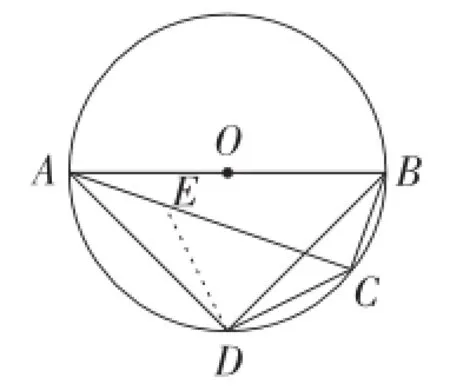
图12

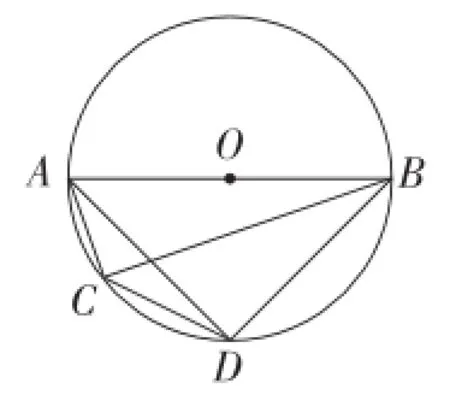
图13

在图12，图13中，⊙O均可进行隐身，

即如图14，∠ACB＝∠ADB＝90°，AD＝BD，

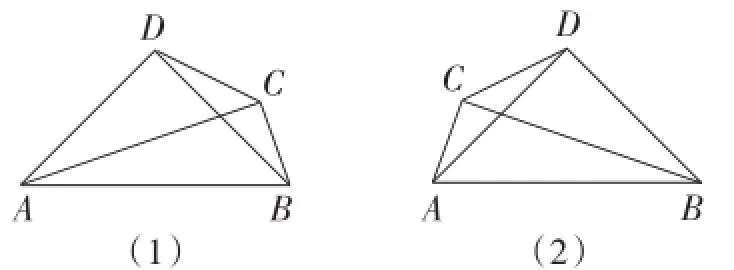
图14

例6 如图15，正方形ABCD的边长为6，点O是对角线AC，BD的交点，点E在CD上，且DE= 2CE，过点C作CF⊥BE，垂足为点F，连接OF，则OF的长为＿＿＿＿＿＿＿．

解：由题意，易知∠BOC＝∠BFC＝90°，OB＝OC.

因为BC＝6，EC＝2，

在Rt△BCE中，

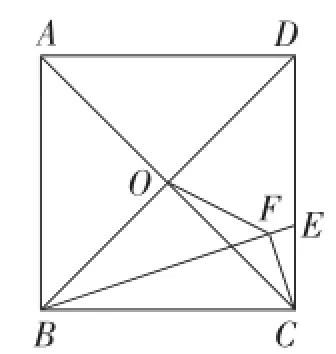
图15

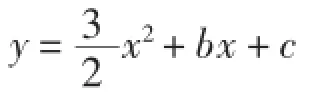
（1）求点C的坐标及二次函数的关系式；

（2）若运动过程中直尺的边A′D′交边BC于点M，交抛物线于点N，求线段MN长度的最大值；

说明：点与抛物线的位置关系可分为三类，例如，在图17中，点A在抛物线内，点C在抛物线上，点D′在抛物线外．

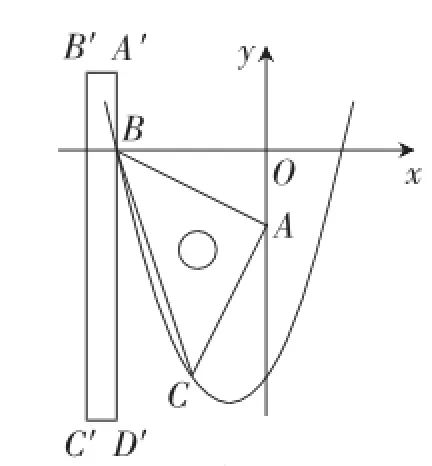
图16

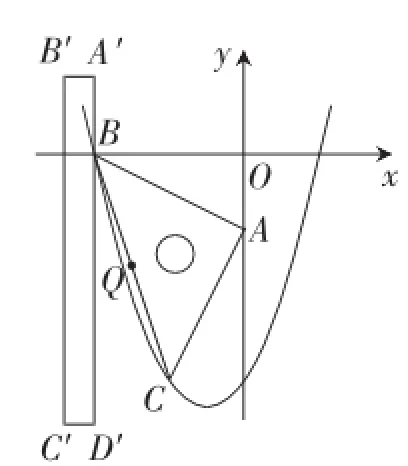
图17

解：（1）略.

（2）略.

（3）如图18，连接AQ．

图18

因为点Q是BC的中点，

所以BQ=CQ=AQ=PQ.

于是点P在△ABC的外接圆⊙Q的两段弧上．

当点P在抛物线外（即点P1）时，

当点P在抛物线内（即点P2）时，

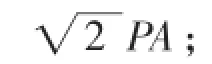
当点P在抛物线上时，若点P在点B处，则PC＝

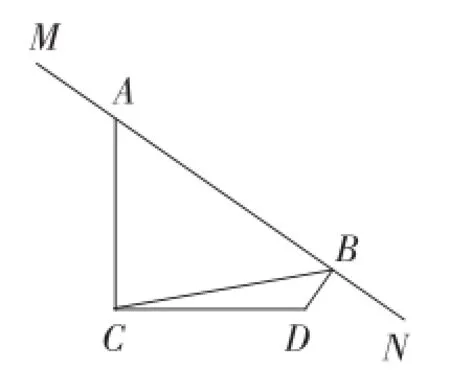
图19

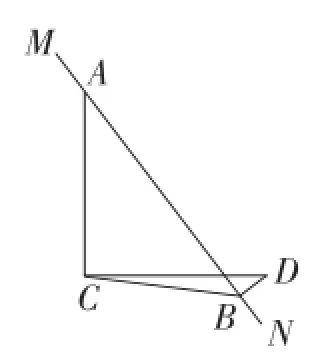
图20

（2）当MN绕点A旋转到如图20和图21所示的两个位置时，BD，AB，CB满足什么样的关系式？试写出你的猜想，并对图21给予证明．

（3）MN在绕点A旋转的过程中，当∠BCD＝30°， BD＝时，则CD=＿＿＿＿＿＿，CB＝＿＿＿＿＿＿．

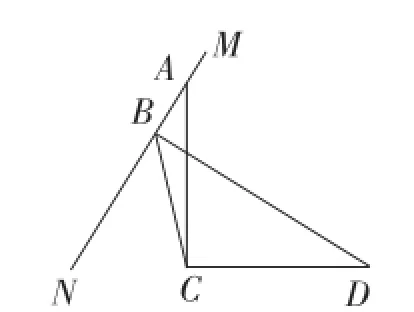
图21

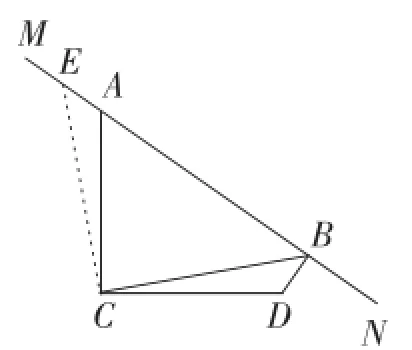
图22

证明：（1）如图22，过点C作CE⊥CB于点C，与MN交于点E．

因为∠ACB+∠BCD＝90°，∠ACB+∠ACE＝90°，

所以∠BCD=∠ACE．

因为四边形ACDB内角和为360°，

所以∠BDC+∠CAB＝180°．

因为∠EAC+∠CAB＝180°，

所以∠EAC=∠BDC.

又因为AC=DC，

所以△ACE≌△DCB.

所以AE=DB，CE=CB.

所以△ECB为等腰直角三角形．

又因为BE=AE+AB，

所以BE=BD+AB.

（3）当点A，B在CD同侧时，易知点A，C，B，D在同一个圆上.

作四边形ABDC的外接圆，如图23所示，

图23

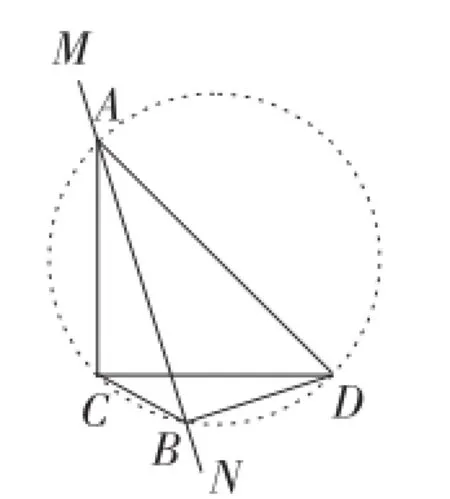
图24

当点A，B在CD异侧时，如图24所示，

四、模型一般化

若将“直角三角形外接圆截直角平分线”模型中的直角三角形弱化为一般三角形，此时线段AC，BC，CD之间又有什么等量关系呢？

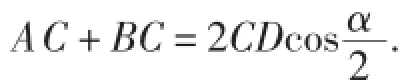
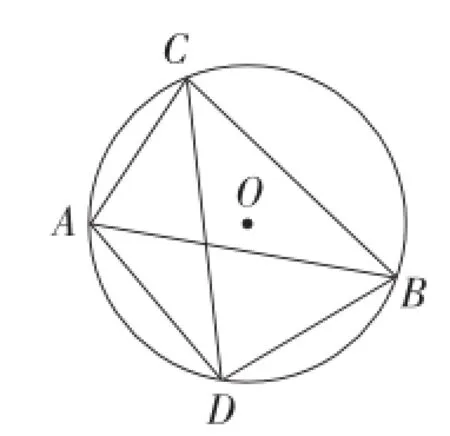
图25

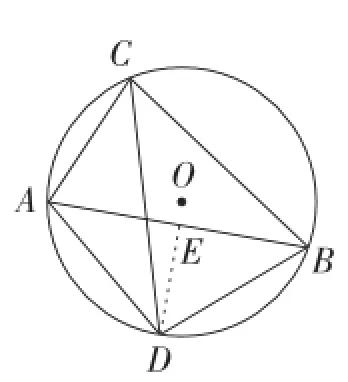
图26

证明：如图26，过点D作DE⊥AB于点E.

因为CD平分∠ACB，

所以∠ACD=∠BCD.

所以A（D=B（D.

于是AD=BD.

又因为DE⊥AB，

所以AE=BE．

在Rt△ADE中，

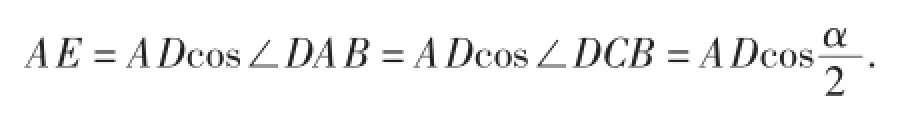
由托勒密定理，得AC·BD+BC·AD=CD·AB.

若图25中点C运动到AD（B上时（点C与点D不重合），如图27所示，此时仍有AD=BD，

说明：图25，图27中的⊙O仍可进行隐身.

至此，我们得到了“三角形外接圆截三角形角平分线”模型的一般性结论，这揭示了命题中条件与结论之间的内在联系.

例9 如图28，半圆O的直径AB=10 cm，弦AC=6 cm，AD平分∠BAC，则AD的长为（）.

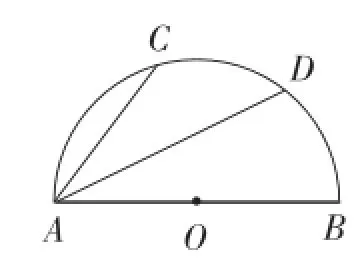
图28

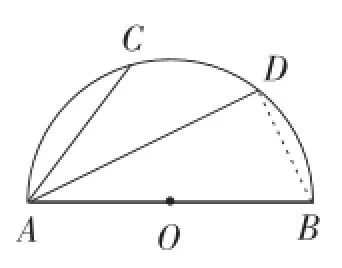
图29

解：如图29，连接BD.

因为AB为⊙O的直径，

所以∠ADB=90°.

故选择选项A.

总之，初中数学试题中可以运用的模型还有很多，教师在平时的教学中要引导学生化题为型，帮助学生通晓其方法，辨识其变化，由“明一理”到“通一片”，积累解题经验，提升解题能力.

参考文献：

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.

［3］王元友.基于“一线三等角模型”的创新能力综合题设计［J］.中国数学教育（初中版），2012（5）：32-34.

［4］陈德前.模型烹大餐教学得启示［J］.中学数学教学参考，2013（7）：48-50.

［5］唐芬.半角模型的纵横迁移［J］.中学数学教学参考，2014（5）：42-44.

收稿日期：2015—10—09

作者简介：王云峰（1971—），男，中学高级教师，主要从事课堂教学、解题教学研究．