“以数助形巧拼正方形”教学设计点评

刘案清（广东省珠海市斗门区教育科研培训中心）朱文芳（北京师范大学数学科学学院）



附：数学实验报告

“以数助形巧拼正方形”教学设计点评

刘案清（广东省珠海市斗门区教育科研培训中心）
朱文芳（北京师范大学数学科学学院）

摘要：广东省珠海市斗门区实验中学的梁洪源老师，设计了“以数助形巧拼正方形”一节课.他通过回顾�的产生过程，让学生通过亲身的实践操作，解决两个或多个小几何图形剪拼为一个大正方形的问题，从而学习“以数助形”的思维方法，体会数形结合的思想方法.

关键词：数形结合；正方形；以数助形

“以数助形巧拼正方形”一课依照著名数学家华罗庚的诗句设计课堂教学结构，鲜明地体现出数形结合数学思想的价值，构造完备的课堂教学环节，突出数形结合数学思想方法培养的同时，注重学生思维品质的培养，并不失时机地培养学生良好的情感、态度及价值观.课堂教学生动、高效、趣味性强.整个教学流程主线分明，数学操作实验特色鲜明，让学生在“思—做—思”中感受数学学习的乐趣.

教学过程具体体现在可操作性强，趣味性浓.教学内容选材新颖，切入角度符合学生的认知层次，以人教版教材七年级下册第41页的探究作为引例，勾起学生的回忆，门槛不高且趣味性强，能起到集中学生注意力、调动学生学习兴趣的作用.通过师生的共同回忆、分析探索、实验操作等环节，初步建立起从“图形剪拼”到正方形边长a的确定，突出了“以形助数”的建模思想.紧接着又以“面积的不变性”为主线，抓住正方形边长的代数式的结构特征，来探索构造新的直角三角形，充分体现了“以数助形”的数学思想.设计中所采用的“剪拼”操作实验的价值不仅仅在剪拼结果的获得，更重要的是在剪拼的过程中借助数式的恒等变换来探索图形的全等变换的过程，从而找到图形变换的方法，并着重引导学生了解、体验剪拼的过程，引导学生理解在剪拼过程中运用了平移、旋转、对称等几何变换，让学生在先“思”后“做”的过程中，深刻掌握几何变换.每一小环节中又以著名数学家华罗庚的诗句作为环节的小结点睛，既富有诗意，又切合题意.

为了使这节课更具探讨性，笔者提出如下问题，供教师展开讨论.

一是本节课是以勾股定理为依据，巧拼大正方形.我们知道，事实上，勾股定理的证明也是用的面积割补法，而且，从古至今，人们创造了几十种割补方法，都能给出勾股定理的验证.结合这节课的内容，这是否会产生逻辑循环？

二是无论是大、小两个正方形，还是一个正方形与一个三角形，拼出一个大正方形都要化归为如图1所示的形式，甚至在教学过程的最后环节归纳出这样拼法的步骤，是否有限制学生思维，使之机械僵化之嫌？事实上，如果是巧拼的话，放手让学生自己动手做一做，笔者觉得拼法应该是多样化的，而非这节课中的最终只有这一种拼法.

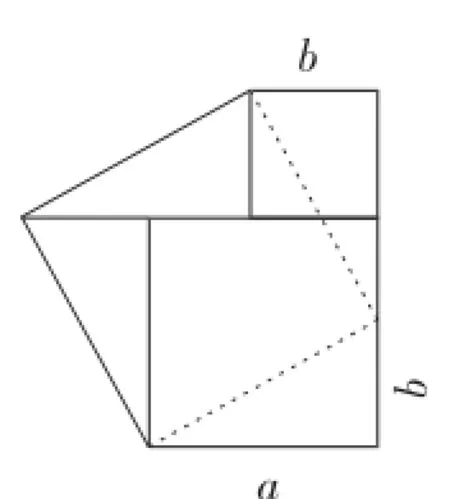
图1

参考文献：

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.

作者信息：刘案清（1966—），男，中学高级教师，主要从事中学数学教材、教法、学法研究.

收稿日期：2015—11—29