中考数学复习课教学形式的探究

■鞠红军

中考数学复习课教学形式的探究

■鞠红军

单元复习课是初中数学教学过程中的重要环节，本文从三维目标入手，举例设计了若干教学形式，分析了创设有效教学情境、发挥教师组织引导性和学生主体性在教学过程中的重要作用。

教学形式数学复习课学生主体

单元复习是九年级数学总复习的重要形式，如何上好单元复习课是一个值得研究的课题。现笔者以我校学生为主体，以问题作导向，结合“分步递进、分层达标”的课型模式，谈谈自己的一些看法。

什么才是一节好的复习课？笔者认为至少要满足以下3点：

一是帮助学生回顾过去所学的知识并形成良好的知识结构；二是帮助学生掌握复习方法、思路、规律与技巧；三是掌握重点知识、突破难点，提高学生灵活应用、解决问题的能力。

下面分步骤进行详细说明：

分步一:知识梳理

目标一:借助问题串，形成系统知识体系

从当前的课堂教学看，部分教师只关注“温故”忽视“知新”，教学过程中通过纯粹的知识梳理，教师一讲到底，教师讲得累、学生听得苦，教学效果往往不好。其实一样的教学内容，若使用不同的教学方法，可以产生不同的教学效果。

笔者认为单元复习课应该是“以问题为中心”的课堂教学。即：根据复习教学目标，设计一定量的、有一定衔接性和过渡性的问题，而且设计的问题要有层次，分步递进。让学生在问题解决过程中，不仅能熟悉知识、优化知识结构，而且通过问题的解决，掌握方法与规律，提升灵活应用知识和分析解决问题的能力。

一般可通过问题串来引领，将复习的重心前移，形成系统的知识体系。

案例1复习“整数（一）”

1.用代数式表示：x的3倍与5的差；一套校服上衣a元，裤子比上衣便宜15元，裤子______元；钢笔每支a元，笔记本每本b元，2支钢笔5本笔记本共花费_______元。市区共有绿地20000平方千米，共有60万人，则人均占有绿地_______平方米。

2.你能再说出代数式“2a+5b”表示的实际意义吗？

3.再增加几个代数式：3x2y，，2x3y2+ x2y-8，你能找到其中的整式吗？还有些式子是什么类型？

4.你所找的整式中哪些是单项式？哪些是多项式？如何区分？

5.单项式3x2y的系数与次数，你如何确定？

6.多项式2x3y2+x2y-8的次数与项数分别是？

7.在多项式2x3y2+x2y-8中有同类项吗？如何判定同类项？说一个3x2y的同类项。

8.试计算2x3y2-3（2x3y2+x2y-8），并求当x=1，y=3时这个代数式的值。

设计目的：课堂伊始，笔者通过这组练习让学生开始一段探究之旅，学生对上述八个问题串的思考与回答，反映出其对代数式知识的掌握情况，便能大概了解学生对该部分知识已有的知识结构。这组习题弥补了不同层次的学生对知识的缺漏，有助于学生在这节复习课中形成系统的知识体系。教师在教学过程中只需要适当地引导，即可帮助学生形成清晰的知识网络，扮演好“先行组织者”的角色。

分步二:例题精讲

目标二:掌握解题技巧，拓展思维

例题教学是复习课中另一重要支撑点，然而，教师们在热衷于精选例题的同时却忽视了对例题教学技巧的探究。如何使学生成为例题教学的主体，笔者采用如下方式进行。例题给出后，应给出足够的时间让学生独立思考，然后请学生说说自己审题的过程，审完题，让学生讲解解题思路，从何处切入。必须说清楚思维过程，注重变式训练。久而久之，就培养了学生对问题的把控，提高了学生分析问题和解决问题的能力。面对难题，教师也不必直截了当地讲解，应该考虑到学生的“最近发展区”，像剥洋葱一样一层一层进行。即点拨——思考——再点拨——再思考，直至揭底。

学生的学习具有积累性，因此教师对例题的选择要具有代表性，要注意题目价值的多元化，即题目能够一题多解、一题多变，能起到举一反三的作用，从而刺激学生的探究欲望，激发学生良好的复习情绪。

案例2当a=-2，b=-3时，求代数式2a2-3ab-b2的值。

教师点拨：解决这类问题可以直接代入有理数进行运算，如果给出的是一个代数式的值，如何求另一个代数式的值？

变式已知a-b=-1，求a3+3ab-b3的值。

教师点拨：由已知条件a-b=-1，我们无法求出a，b的确定值，因此本题不能像案例2代入a，b的值求代数式的值。

解法1由a-b=-1得a=b-1，代入所求代数式化简：

a3+3ab-b3

=（b-1）3+3（b-1）b-b3

=b3-3b2+3b-1+3b2-3b-b3

=-1

教师点拨：这是用代入消元法消去a化简求值的。

解法2因为a-b=-1，所以

原式=（a3-b3）+3ab

=（a-b）（a2+ab+b2）+3ab

=-1×（a2+ab+b2）+3ab=-a2-ab-b2+3ab

=-（a2-2ab+b2）

=-（a-b）2

=-（-1）2

=-1

教师点拨：这种解法是利用了乘法公式，将原式化简求值的。

解法3因为a-b=-1，所以

原式=a3-3ab（-1）-b3

=a3-3ab（a-b）-b3

=a3-3a2b+3ab2-b3

=（a-b）3

=（-1）3

=-1

教师点拨：这种解法巧妙地利用了-1=a-b，并将3ab化为-3ab（-1）=-3ab（a-b）从而凑成了（a-b）3。

设计目的：通过对精选典型例题的剖析和深化，进一步巩固复习内容，训练了基本技能，学生领悟了思想方法，积累了基本经验。在交流时，重在引导学生进行分析，强化解题思路的探索，重视规律和方法的总结，不仅授之以鱼，而且授之以渔。

分步三:归纳总结

目标三:注重知识内化，实现整体升华

在课堂结尾部分，有必要引导学生对所学知识技能再次总结升华，提炼出知识结构。在这一阶段，笔者多让学生自主建构，整体感知整章单元的知识结构，理解其中的联系。

案例3请同学们从以下几个方面谈谈自己的收获。

（1）今天你学会了什么知识？

（2）掌握了哪些方法？

（3）解决了哪些问题？

（4）你还想继续了解什么？

（5）哪位同学能上黑板画出本节课的知识结构图？

学生一（回答）：……

学生二（回答）：……

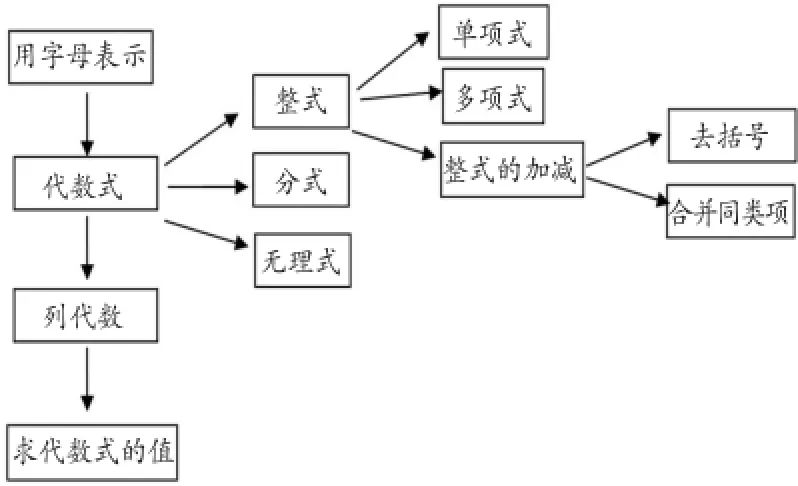
设计目的：让学生从知识技能、思考过程和方法、情感态度和价值观等方面对本节课的三维目标进行总结反思，目的是进一步帮助学生掌握知识、突破难点，提升解决问题的能力。同时通过知识点的网络化，帮助学生更加全面深入理解掌握整式的相关知识。在夯实基础的同时，学以致用。

结束语：单元复习课只有把握本章单个知识的本质属性和各知识点间的联系，将前后知识串联起来，帮助学生掌握复习方法、思路、规律与技巧，才能提高学生灵活应用，解决问题的能力。在课堂上注重发挥学生的主体性，推动学生的认知能力纵深发展，有利于学生完善认知，加深记忆，提高能力，进而提高复习效益。

（作者为江苏省扬州市田家炳实验中学教师）