初中数学教学中的情境创设与对比分析——以直角三角形的性质推论为例

■诸春妹

初中数学教学中的情境创设与对比分析
——以直角三角形的性质推论为例

■诸春妹

本文通过对比同一课题不同教学情境的创设，揭示了不同情境下的教学效果，说明了数学教学中创设教学情境的必要性，也为自己和广大教师提高教学水平和拓展课堂资源提供一些新的思路。

数学课堂情境创设

随着教学改革的推进，课堂教学的实效性得到越来越多教师的关注。数学教师的任务，在于把数学的学术形态转变为学生易于接受的教育形态。情境创设是教师创造性的行为，是开展教学活动的基本要求，是教学过程的重要环节。良好的情境创设，能调动学生学习数学的兴趣、促进数学知识的理解和迁移、发展思维能力。但有些教师在评优课教学中刻意追求新鲜题材、争取出人意料，有时反而会给人以哗众取宠之感。为此，我们不得不思考，究竟该如何把握情境教学的“度”。下面笔者结合多年教学实践经验，通过比较几个相同课题的不同情境设计谈谈自己的体会。

近几年来，沪教版教材八年级上册直角三角形的性质定理推论“直角三角形中斜边上的中线等于斜边的一半”一直是开设公开课的热门课题。一个好的课题引入情境设计，往往会成为一堂课成功的关键，更能提高学生对新知识的兴趣。当然，要提高学生对新知识的兴趣，更重要的是情境引入要有合理性和必要性，这样就能让学生信服，并产生想要学的欲望。也正因为深刻认识到这一点，我在上这节课的时候潜心让自己尝试不同的教学情境，针对所教授的不同届学生，从以下几个教学情境出发，观察学生的课堂反应，以此不断改进自己的教学方式。

情境设计一

设计作业纸：在作业纸上画好一个直角三角形。请同学们找斜边上的中线并填充下面的表格。

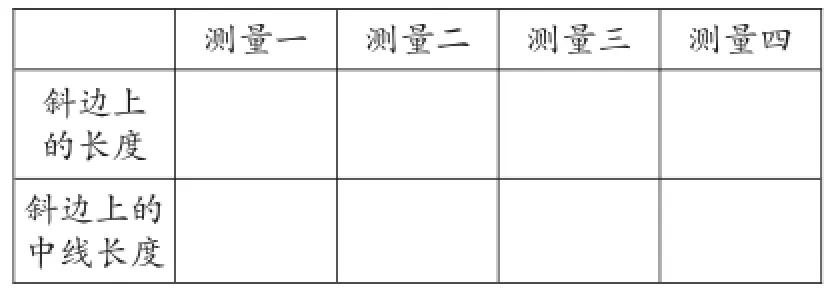
表1

学生课堂反应：以四人为一小组展开讨论，先让同学们找到斜边上的中线，有个别小组找不到中线的，教师在旁边加以指导。当时学生在测量时的表现较为积极，但对数据的测量出现了很大的误差，有同学甚至不知道如何准确测量所需要的数据。而有的同学事先预习了，他不测量也能直接得知结果。

反思：学生通过测量过程来理解直角三角形斜边上的中线等于斜边的一半，看上去课堂气氛热闹，整个定理的发现由学生自主完成，充分发挥了学生学习的主动性，新教材也一直在情境设计教学这一块鼓励教师通过学生实验操作得到所要的结论，希望从“实验——归纳——应用”这样的教学让学生体验知识形成的过程，然而，一届届不同学生的反应让这样的教学情境显得有点为操作而操作。

情境设计二

直接出示图形，如图1，观察圆中的OC与AB之间的数量关系，并猜测△ABC是什么形状的三角形。

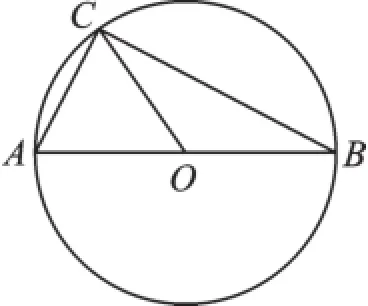
图1

学生课堂反应：学生能直接从半径与直径的概念中得出它们之间的数量关系。之后抛出的问题是三角形的形状，大部分学生能猜出直角三角形，而对这个结论的论证方式只有个别同学想到了。突破这个难点后，提出它的逆命题的形式并进行验证。

反思：这样的设计比较直接，但是由于以逆命题的形式给出，似乎在数学情境设计中没有体现出数学的严谨性要求。这样的设计并没有从学生的实际出发，有些本末倒置了。

情境设计三

设计作业纸：想一想，在一个直角三角形中是否能一次同时剪出一个等腰三角形和一个等边三角形？如果能剪出，此时的直角三角形的锐角要满足什么条件？

给出一个含有30度角的特殊直角三角形，如图2，让学生组成学习小组进行讨论。

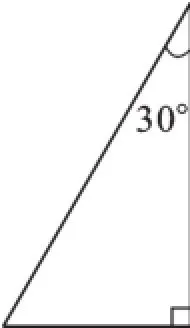
图2

学生课堂反应：教师问题一提出，课堂气氛明显有点沉闷，学生一头雾水，不知从何处入手，而且学生对分解图形本身就没方向。只有部分学生看到“等边三角形”能联想到这个直角三角形两个锐角的度数，从而把一条直角边作为初始边来找三角形，但绝大部分学生只是看着图形，胡乱地画着线。

反思：新课程基本理念指出，“数学课程应突出体现基础性、普及性和发展性，使数学教育面向全体学生，实现人人学有价值的数学，不同的人在数学上得到不同的发展。”这样的设计显然激起了一部分学生在学习活动中的学习斗志，让学生在经历中以学会主动探索和解决问题为立足点，鼓励他们大胆猜想，激发学生的创新意识，最终把知识结构转化为学习者的认知结构。但也让大部分学生感觉难度太大，不知这样做的明确目的是什么。而后只能由教师引领学生一起找到60度角再构造等腰三角形，但这样的情境引入耗时太长，不能直接切入主题。

情境设计四

从尺规作图出发，学生刚学完尺规作图，在含有30度角的直角三角形中，让学生以其中一个直角顶点为圆心，以较短的直角边为半径画弧，如图3。

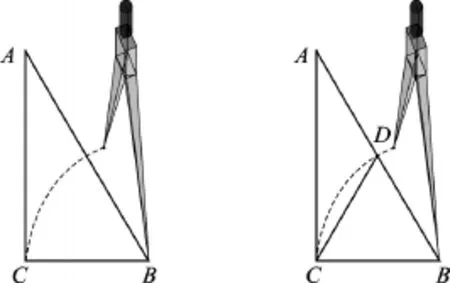
图3

利用多媒体的几何画板将动态的效果展现在学生面前，明确找到了点D的位置后，让学生去发现CD线段在直角三角形中的名称以及它与斜边之间的数量关系。

学生课堂反应：通过多媒体课件的演示，呈现知识形成的过程，让学生有思考的欲望。有些内容过去单凭教师“说”，学生不好理解，现在多媒体能帮助教师“说话”，把抽象和直观有机结合起来，情况就大不相同了。学生对于课件中出现的CD线段，能很快把握其与斜边之间的数量关系，因而结论的揭示对大部分学生都并无困难。

反思：多媒体课件中几何画板的运用加深了学生对中线的认识，并在不断改变的直角三角形图形中发现斜边上的中线与斜边之间不变的数量关系，直观而且深刻，也让学生体会了从特殊到一般的数学思想方法。这样的设计既直观明了，又切入知识要点，揭示出课题，也充分利用了多媒体与数学的完美整合，相当受学生的欢迎。

情境设计五

如图4，用多媒体给出一个等边三角形与一个底角为30度的等腰三角形（其中等边三角形的边与等腰三角形的腰相等），首先通过对这两种特殊三角形性质的复习，引出直角三角形作为特殊的三角形隐含什么样的性质，然后通过几何画板演示这两个三角形的叠合过程，让学生在图形动态过程中得到了直角三角形。如图5，此时等边三角形的边与等腰三角形的腰叠合在一起，它便成为了直角三角形中一条特殊的边。

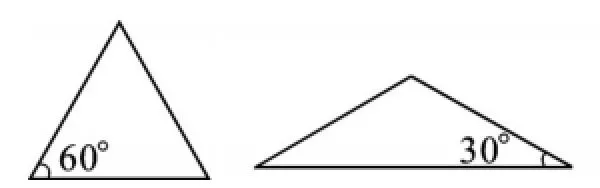
图4

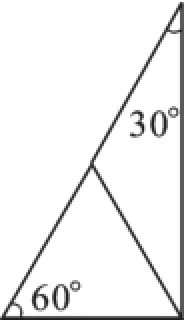
图5

学生课堂反应：学生在课件的演示过程中立即就能够得出“斜边上的中线等于斜边的一半”这个结论，并为辅助线的添设做了铺垫。

反思：课堂上每一位学生都认真地看着课件中图形的生成过程，多媒体课件不仅从视觉上给学生以足够的冲击，动感十足，大大提高了学生的探究热情，也让定理的得出水到渠成，论证的方法通过课件的展示迎刃而解。这种设计从学生已有的知识出发，帮助学生找准新旧知识的连接点，在新旧知识之间建立起非人为的实质性联系，实现认知迁移，使学生能够利用旧知同化新知，从而学会学习。

通过这几个情境的教学设计，我不断思索着什么样的情境教学更适合学生，也正是这样的不断改进，我和我的学生更加知道学习数学的乐趣。特别是情境四和情境五，让我的学生眼前一亮，原来知识可以这样来学习。因此情境的设计并不是简单地照搬教材，还必须符合学生的认知水平，从学生现有的知识出发，避免知识的跳跃，做到慢慢深入、合理衔接，使其变成更能激发学生探究热情的引入，让学生真正成为学习的主人。

总之，情境教学在数学教学中的作用重大，对全堂课起关键的引导作用，同时情境教学是发挥学生主动性的重要途径，有利于学生数学建模意识的构建与学生创造性思维的培养。作为一名一线教师，要合情、合理地进行情境教学，但要切记情境教学不可喧宾夺主、虎头蛇尾、偏离主题甚至出现反面教材。

（作者为上海市奉贤区清溪中学教师）