知识“点”，方法“线”，思想“面”——九年级《平面直角坐标系中的“点”》专题复习课教学实录

■张　扬

知识“点”，方法“线”，思想“面”
——九年级《平面直角坐标系中的“点”》专题复习课教学实录

■张扬

（一）设计数学情境，展示函数和平面直角坐标系之间的关联

师：同学们，今天我们一起来复习一下《平面直角坐标系中的“点”》这节课的知识内容。

（教师先画出如图1所示的平面直角坐标系，标出A（2，1）、B（6，4）两点的位置）

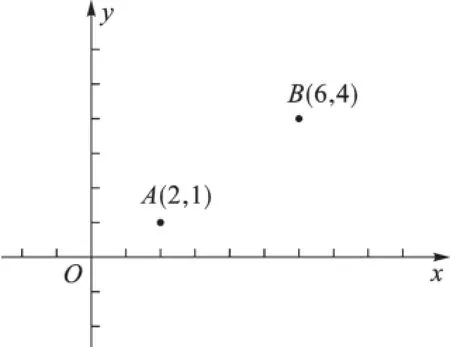
图1

师：请同学们根据图中的信息，设计一个问题，并简述这个问题的求解思路。

生1：求直线AB的解析式，用待定系数法求解。

师：是的。能否求出经过A（2，1）、B（6，4）两点的双曲线的解析式？

生1：不能，已知一点就可以确定双曲线的解析式了。

师：那A（2，1）、B（6，4）两点所确定的双曲线的解析式各是什么？

师：当A、B两点在同一条双曲线上时，这两点的坐标需具备什么条件？

生1：这两点的横、纵坐标之积相等。

师：你能举个例子吗？

生1：如A（2，1）、B（1，2）或A（4，6）、B（6，4）等。

师：能确定经过A（2，1）、B（6，4）两点的抛物线的解析式吗？说说理由。

生2：不能，因为方程组有无数个解，那么，经过A（2，1）、B（6，4）两点的抛物线就有无数条。

师：何时经过A（2，1）、B（6，4）两点的抛物线只有一条呢？

生2：当这两点中的一点是抛物线的顶点时，这条抛物线就是唯一确定的。

师：将“坐标平面内的点的个数”与“确定函数的解析式”之间的关系总结一下。

生2：（略）

【启示】函数与平面直角坐标系紧密相连，学生很容易由平面直角坐标系中的点联想到过点的函数图像，然后利用待定系数法，构建方程组求函数解析式，这也是学习平面直角坐标系的核心。

（二）定点与动点结合，展示数学问题模型

师：回到图1中，你们还能够设计出什么问题？

生3：求A、B两点之间的距离。

师：涉及哪些知识点？说具体些。

生3：过点A、B分别作x轴的垂线段交x轴于点C、点D，再过点A作AE⊥BD于点E，在△ABE中，利用勾股定理求解。（如图2）

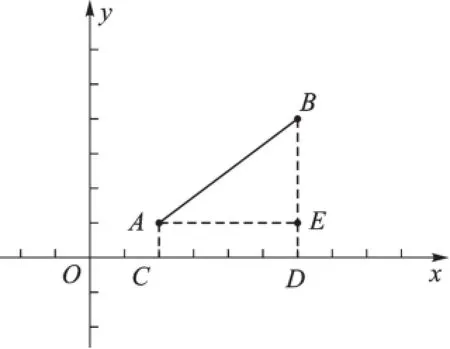
图2

师：现在添加一个动点M（m，0），继续设计关于点A、B、M的数学问题。

生4：因为点M（m，0）在x轴上，当MA+MB的值最小时，求点M的坐标。

师：首先要找到这个点，它在哪里？

生4：找点A关于x轴的对称点A′，连接A′B，与x轴的交点就是所要找的点M（m，0），此时MA+MB最小，最小值就是线段A′B的长度。

师：为什么？

生4：在x轴上另取一点M′，不与点M重合，连接AM′、BM′、A′M′，此时AM′+BM′=A′M′+ BM′，在△M′A′B中，A′M′+BM′＞A′B，所以A′B最小。（如图3）

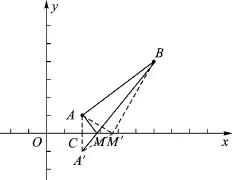
图3

师：这就是著名的“将军饮马”问题，也是“最短距离”的数学模型。由“和的最小值”可以联想到什么问题？

【启示】什么是数学的“魂”？通过一题多解与多题一解，达到探究一个问题、掌握一种办法、解决一类问题的能力和水平，这就是数学的“魂”！也就是说，判断数学是否有“魂”，关键就在于能否将一个知识点灵活地迁移运用到新的认知情境中。

生4：在x轴上找一点M（m，0），使得|MA-MB|最大，求点M的坐标。

师：这个点M（m，0）的位置在哪里？先独立思考，然后再互相讨论一下。

生4：如果在x轴上取一点M′，连接AM′、BM′，这时|M′A-M′B|＜AB。（如图4）

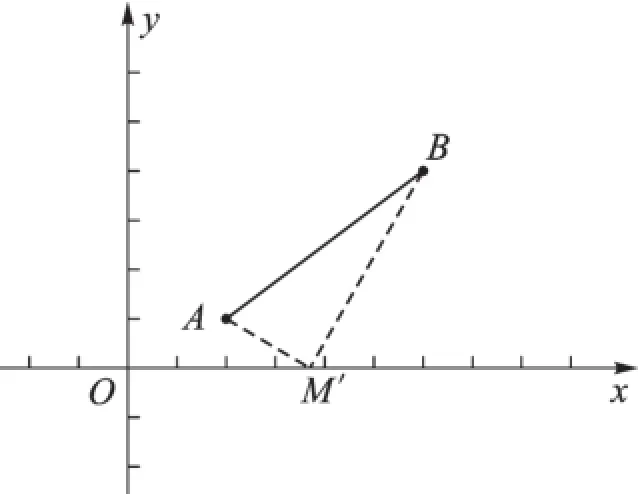
图4

师：是否存在|M′A-M′B|=AB呢？

生4（思考片刻）：点A、B、M′在同一条直线上时，|M′A-M′B|=AB。

师：请同学们画出点M，为什么此时|MA-MB|最大呢？

生4（画出图5）：|M′A-M′B|＜AB，而|MA-MB|=AB，只有当点A、B、M在同一条直线上时，|MA-MB|最大，最大值就是线段AB的长度。

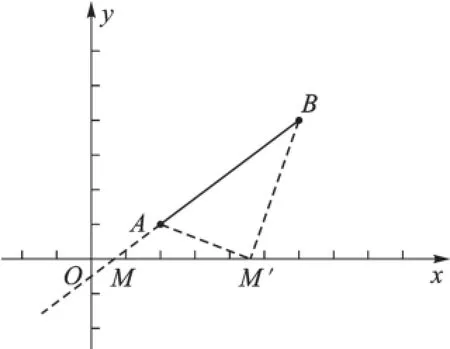
图5

师：运用“比较法”推出M点的位置，进而求出M点的坐标。好，请继续设计问题。

生5：在x轴上找一点M（m，0），使得①MA= AB，②MB=AB，③MA=MB，求点M的坐标。

师：如何找到这些点？试着选择①②③其中之一，求出点M的坐标。

（学生分组，分别求符合①②③条件的点M的坐标，教师巡视。依据学生完成的情况总结）

生6：①当MA=AB时，以点A为圆心，AB为半径画圆，若与x轴有交点，交点就是所要找的点M（m，0）（如图6）；②当MB=AB时，以点B为圆心，AB为半径画圆，若与x轴有交点，交点就是所要找的点M（m，0）（如图7）；③当MA=MB时，作AB的垂直平分线，与x轴的交点就是点M（m，0）（如图8）。

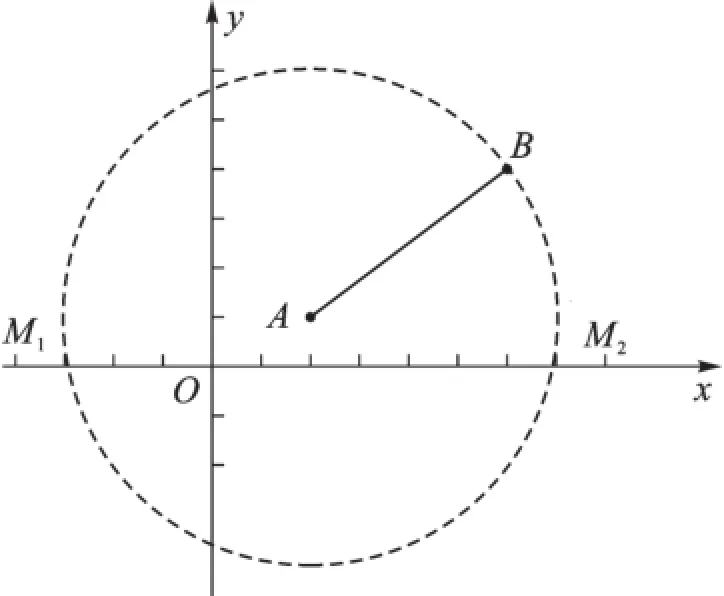
图6

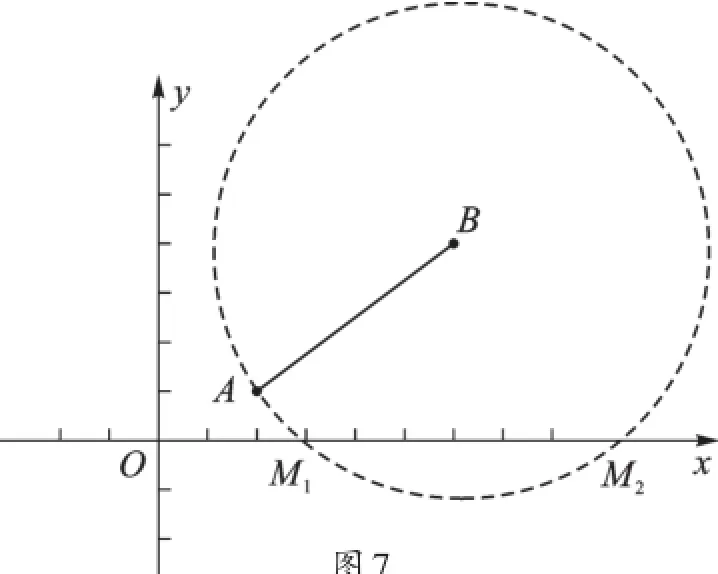
图7

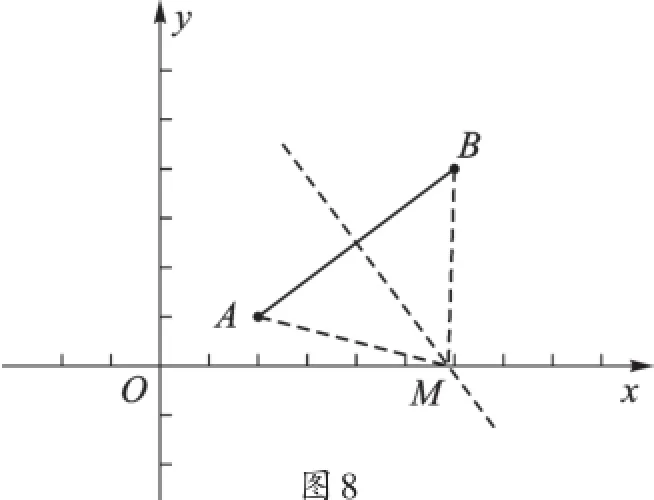
图8

师：符合条件①②的点M的坐标易求，如何求使得MA=MB的点M坐标呢？

生7：求出线段AB的垂直平分线的解析式，再令y=0，即可求出。

师：可以的，但如何求这条垂直平分线的解析式，请课后求解。还有其他方法吗？

生8：利用勾股定理求解。分别过A、B两点向x轴作垂线段，垂足分别为C、D。（如图9）

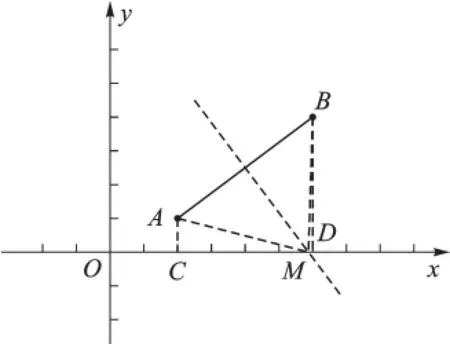
图9

∵AM2=AC2+MC2，BM2=BD2+DM2，AM=BM，

∴AC2+MC2=BD2+DM2，

即12+（m-2）2=42+（6-m）2，

师：如何用一个问题来概括以上三个小问题呢？

生9：在x轴找一点M（m，0），使得△ABM是等腰三角形。

师：这样的点M（m，0）怎么找？

生9：要分三种情况：（1）以∠A为顶角的等腰三角形；（2）以∠B为顶角的等腰三角形；（3）以AB为底边的等腰三角形。

师：由△ABM是等腰三角形，我们又联想到什么问题？

生10：在x轴上找一点M（m，0），使得△ABM是直角三角形，求出点M的坐标。

师：如何找出这样点M（m，0）？

生11：也要分三种情况：①如图10，以A为直角三角形的直角顶点，过点A作AM⊥AB，交x轴于点M，则△ABM是直角三角形；②如图11，以B为直角三角形的直角顶点，过点B作BM⊥AB，交x轴于点M，则△ABM是直角三角形；③如图12，以AB为直径作圆，若与x轴有交点，则交点就是点M。

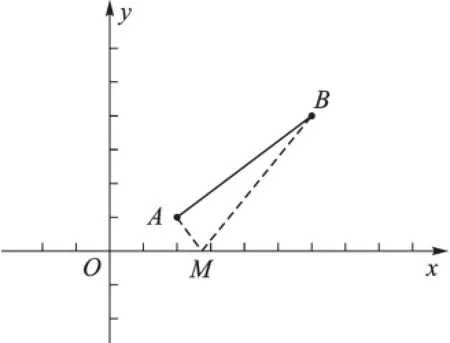
图10

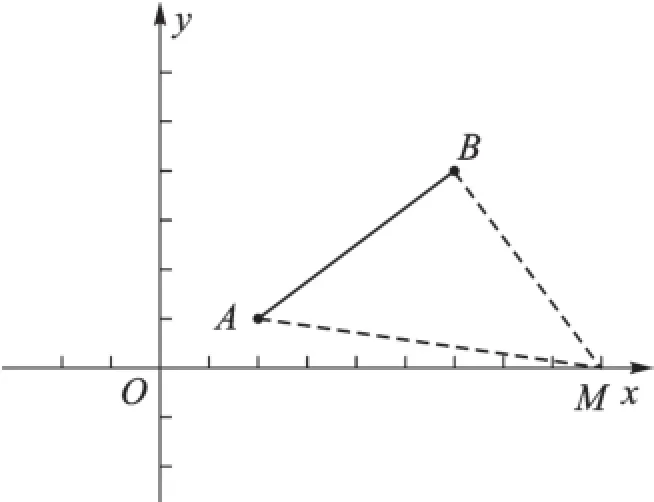
图11

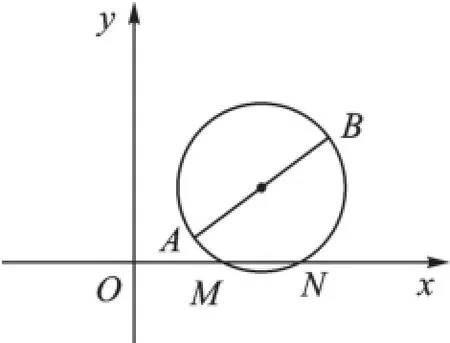
图12

师：每种情况下点M（m，0）的坐标怎么求？我们先来看第一种情况。

生12：如图13，过点A作AC⊥x轴，交x轴于点C，过点B作AC的垂线交AC于点E。易证△AEB∽△MCA，∴，∴CM=，∴m=2.75。

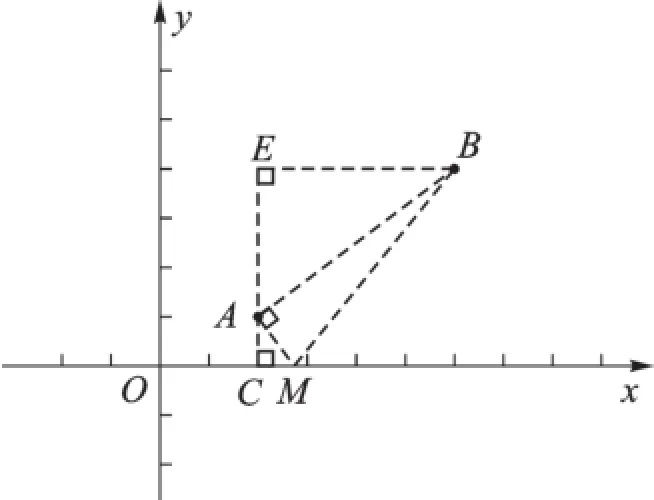
图13

师：再看第二种情况。

生13：如图14，先求出直线AB与x轴交点G的坐标，过点B作BH⊥x轴于点H，可证△GBM∽△GHB，就可以求出点M的坐标。

图14

生14：如图15，过点M作MF⊥x轴，过点B 作BF⊥MF于点F，过点A作AE垂直于FB的延长线于点E，可证△BFM∽△AEB，就可以求出点M的坐标。

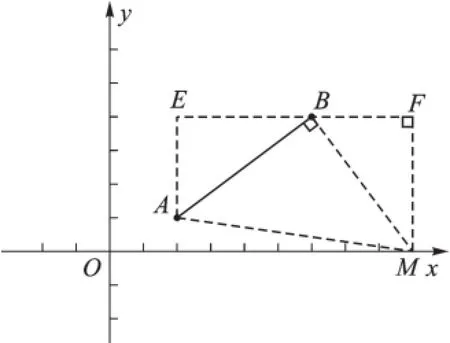
图15

图16

师：那第三种情况呢？

生15：如图16，过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，可证△BDM∽△MCA，就可以求出点M的坐标了。

师：图13、图15和图16的构造有什么共同特征？

生16：都是构造“K”型图，通过三角形相似求得线段的长度来确定点M的坐标。

师：同学们设计的问题很精彩，解决问题更是精彩。

【启示】“你们还设计出什么问题？”“涉及哪些知识点？由‘和的最小值’可以联想到什么问题？”“还能设计什么问题？”“如何找到这些点？”“如何求使得MA=MB的点M坐标呢？”“还有其他方法吗？”“如何用一个问题来概括以上三个小问题呢？”“由△ABM是等腰三角形，我们又联想到什么问题？”“如何找出这样点M （m，0）？”“每种情况下点M（m，0）的坐标怎么求？”随着一个又一个问题的抛出，一步一步引导学生的知识和思维由“点”及“线”，再由“线”及“面”。学生在提出问题、解决问题中自觉或不自觉地进行知识和思维的串联、归类，最终形成某项知识的系统和解决某项问题的系统方法。

（三）课堂小结（略）

（四）布置课外作业

已知两点A（2，1）、B（6，4），解答下面问题：

（1）将线段AB绕着点A顺时针旋转90°得到AB′，求点B′的坐标；

（2）在x轴上找一点M（m，0），使得S△ABM=5；

（3）试求M（m，0）、N（0，n）两点，使得四边形NAMB是平行四边形。

（4）试求M（m，0）、N（0，n）两点，使得以A、B、M、N为顶点四边形周长最小。

【启示】适当、适量、适度的课外作业，既能引发学生进一步攻坚克难的欲望，又能体现数学学习的延续性，从而让数学学习发挥最大的辐射功能和延伸作用。