基于希尔伯特变换的两栖车辆非线性横摇运动模型辨识研究
马新谋, 郝一凝, 常列珍, 潘玉田
(1. 中北大学 机电工程学院, 山西 太原 030051; 2. 中北大学 理学院, 山西 太原 030051)
基于希尔伯特变换的两栖车辆非线性横摇运动模型辨识研究
马新谋1, 郝一凝1, 常列珍2, 潘玉田1
(1. 中北大学 机电工程学院, 山西 太原 030051; 2. 中北大学 理学院, 山西 太原 030051)
摘要:为了识别两栖车辆非线性横摇运动方程, 首先采用希尔伯特变换法把自由横摇衰减信号变换成解析信号, 该解析信号包含了自由横摇运动的瞬时幅值信息和瞬时频率信息, 并给出了两栖车辆非线性横摇运动方程阻尼函数和恢复函数与瞬时幅值和频率的关系式, 最后由最小二乘法拟合拟合即可获得两栖车辆非线性横摇运动方程的非线性阻尼项和恢复项系数. 应用所提出的方法针对数值仿真实例和某两栖车辆1∶4模型自由横摇衰减实验数据, 成功地估计出了非线性参数, 估计值与真值及实验值吻合很好. 估计结果表明所提出的方法可以用于估计两栖车辆非线性横摇运动方程, 而且精度满足工程需求.
关键词:希尔伯特变换法; 两栖车辆; 非线性横摇运动; 包络线; 瞬时频率
两栖车辆在水上的运动为六自由度的运动, 其中横摇运动与船舶横摇运动相似, 是一个非线性振动学问题, 因此两栖车辆非线性横摇运动也成为影响两栖车辆水上安全性、 成员舒适性的重要因素[1-3]. 众所周知, 船舶非线性横摇是影响船舶性能与安全性的重要因素, 特别是在突风载荷、 波浪载荷和流联合激励下, 船舶会发生奇异倾覆[4-9]. 所以有必要针对两栖车辆非线性横摇运动进行深入研究. 要开展两栖车辆非线性横摇运动特性的首要任务是建立非线性横摇运动方程. 到目前为止, 研究船舶横摇运动的工作很多, 常用来建立船舶非线性横摇运动方程的方法有经验公式法[5]和船模自由横摇衰减试验法[4,6-7,9]两种. 对于经验公式法仅对特定的船型适用; 而船模自由横摇衰减试验法适用性强, 应用范围广, 由此演化而来的建立船舶非线性横摇运动方程的方法有最小二乘法[2]、 傅汝德能量法[1]、 改进的能量法[1,4,6]、 遗传算法[6]、 反问题法[7]、 消灭线法、 支持向量机法[9]等, 这些方法都要从自由横摇衰减曲线来识别非线性横摇运动方程的参数.
另一方面, 希尔伯特变换(Hilberttransform,HT)在信号处理、 故障诊断和参数识别领域都有了广泛的应用, 其中关于参数辨识领域的文献也较多.Feldman[10-11]采用希尔伯特变换对非线性系统的各项参数进行了识别研究, 并针对一般形式的运动方程提出了一种自由振动分析方法, 是近期关于希尔伯特变换的经典之作.Shin等[12]把希尔伯特变换在信号处理领域进行了系统的阐述, 给出了不同特征信号的处理技巧.Ignacio等[13]成功用希尔伯特变换估计了铁路桥振动系统的模型参数.Shi等[14]用希尔伯特变换和经验模态公式法从强迫振动信号里估计出了多自由度模型的参数, 表明希尔伯特变换法不仅对单自由度系统适用, 对多自由度系统也适用.Kim[15]用希尔伯特变换法对浮式生产储/卸油装置(FPSO)的自由横摇衰减曲线进行了处理, 成功辨识了FPSO横摇运动方程的非线性阻尼项和非线性恢复项系数, 精度满足工程需求. 从这些成功的范例来看, 希尔伯特变换法也可以用来估计两栖车辆的非线性横摇运动模型参数.
基于上述原因, 本文借鉴船舶横摇运动的研究成果和希尔伯特变换理论, 拟采用希尔伯特变换法来处理两栖车辆自由横摇衰减曲线以估计两栖车辆非线性横摇运动方程的参数.
1非线性横摇方程参数估计理论
借鉴船舶非线性横摇运动研究理论, 不考虑与其他方向运动的耦合效应, 则静水里的两栖车辆单自由度的非线性横摇运动方程可以用二阶常微分方程[1]表示为
(1)
为了方便描述, 式(1)可以改写为
(2)
(3)
(4)
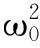
采用希尔伯特变换法估计非线性横摇参数的基本理论是建立在如下的解析信号基础上.

(5)
(6)
式中:pv为柯西主值.
将式(5)改写成幅值和相位表示的复指数形式
(7)
式中:A(t)是瞬时包络线; ψ(t)是瞬时相位角.
由欧拉公式可知, 存在如下关系
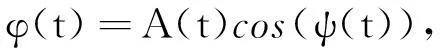
(8)
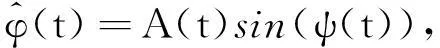
(9)
而且
(10)
(11)

(12)
(13)
式中:ω(t)是瞬时频率, 是时间的实函数.
考虑到式(12)和(13), 计算式(5)的一阶导数和二阶导数
(14)
(15)
对式(2)进行希尔伯特变换, 可得
(16)
将式(16) 乘以虚数单位i再加上式(2)可得用解析信号Y(t)表达的微分方程
(17)
将式(14)和(15)代入式(17), 合并实部和虚部可得
(18)
要使式(18)恒成立, 需要实部和虚部的系数恒为零, 即
(19)
(20)
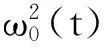
2数值仿真实验
在获得上述信息的基础上, 如图 1 所示, 存在边界效应, 为了使计算方便和可靠, 可以截取信号质量较好的中间部分, 再根据式(10)和(13)可以计算瞬时包络A(t)和瞬时频率ω(t), 如图 2 和图 3 所示. 进而可以计算A(t)和ω(t)的一阶导数和二阶导数.
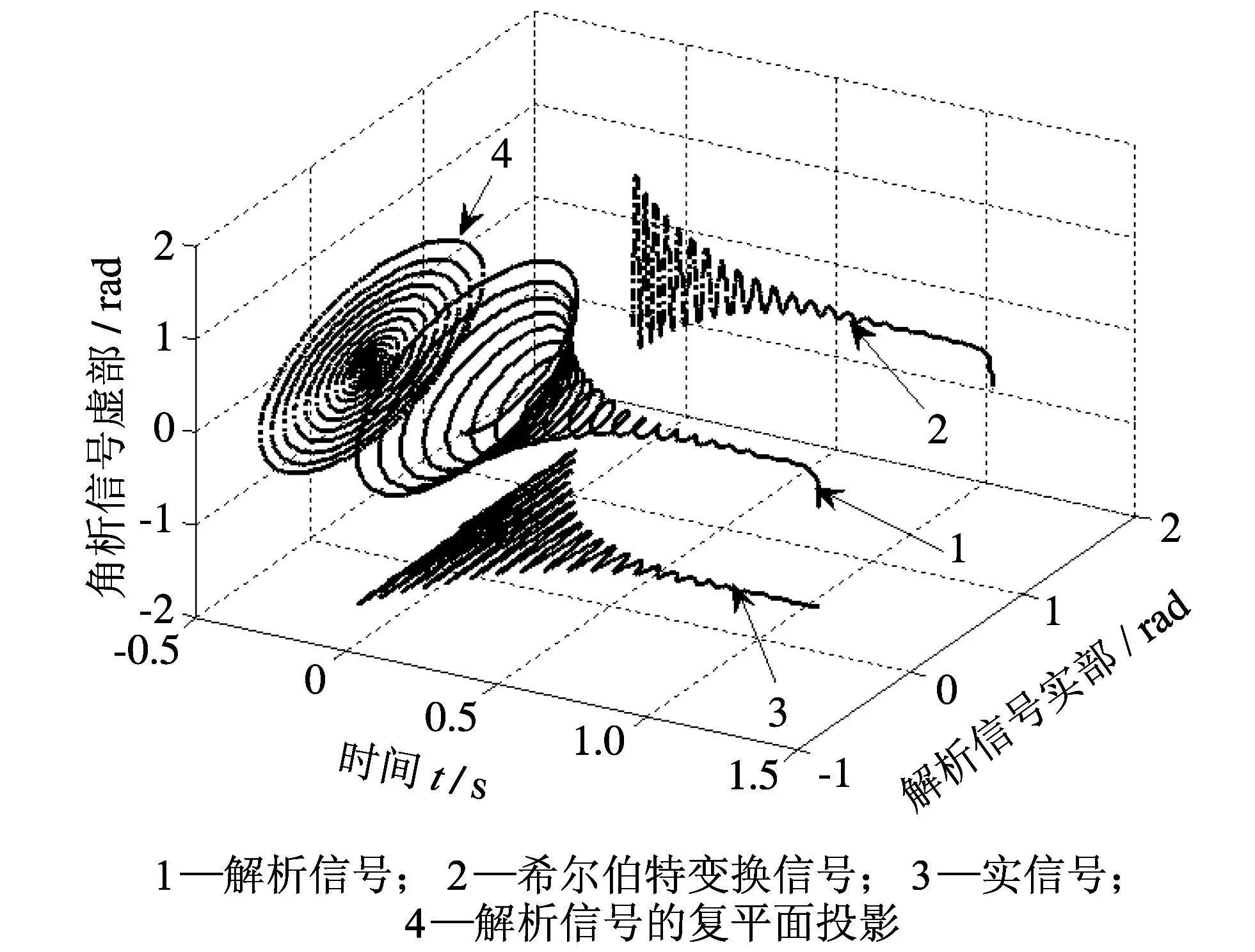
图 1 横摇位移信号曲线Fig.1 Signal curve of roll motion

图 2 自由横摇曲线和包络线Fig.2 Free decay curve and envelope
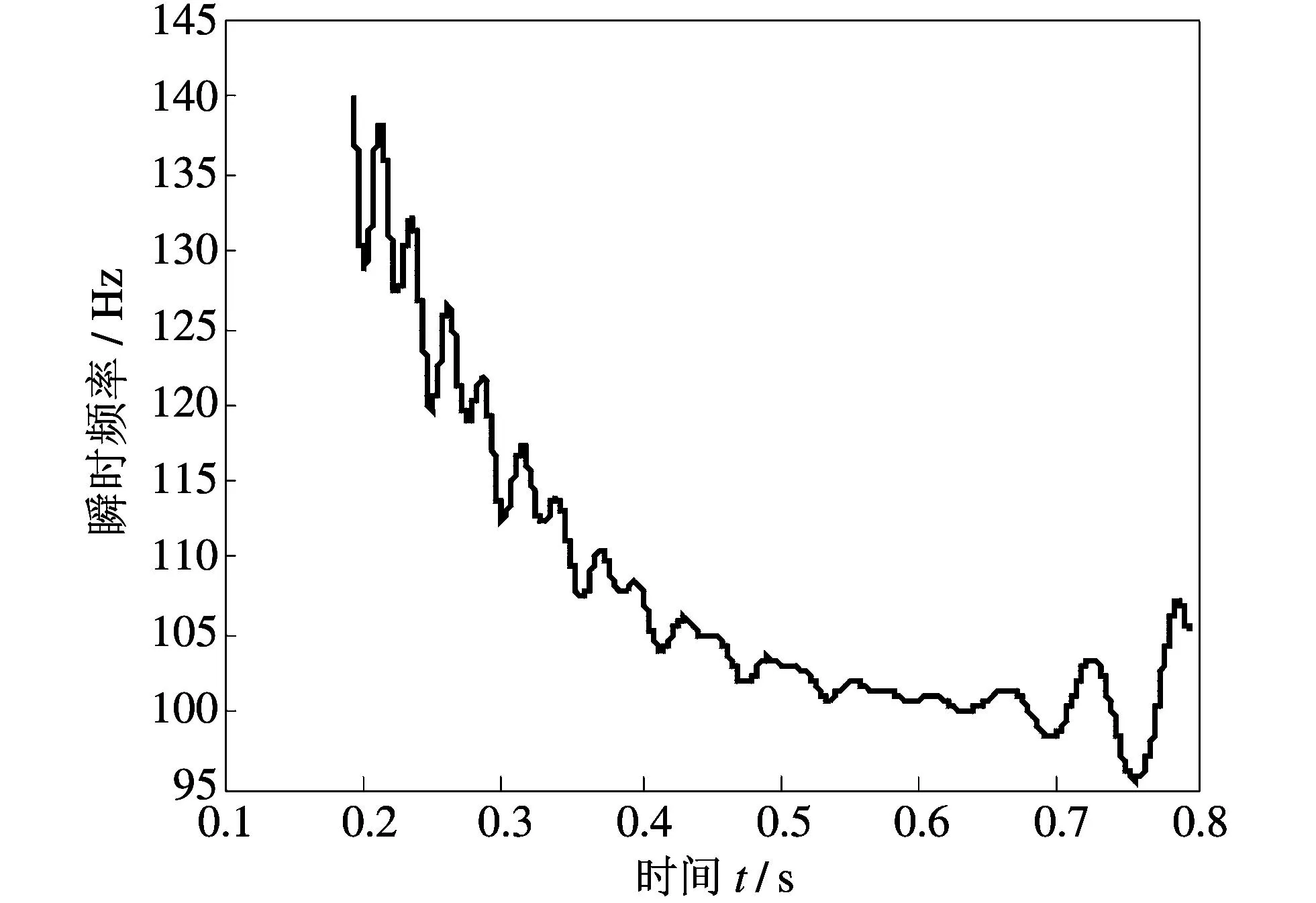
图 3 瞬时频率曲线Fig.3 Instantaneous frequency curve
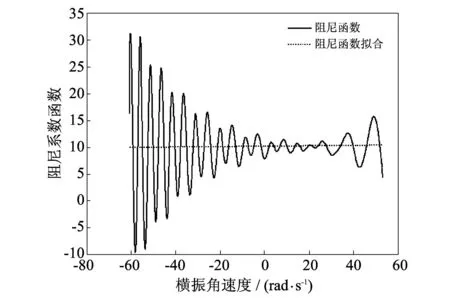
图 4 阻尼函数和拟合曲线Fig.4 Damping coefficients function and fitted curve
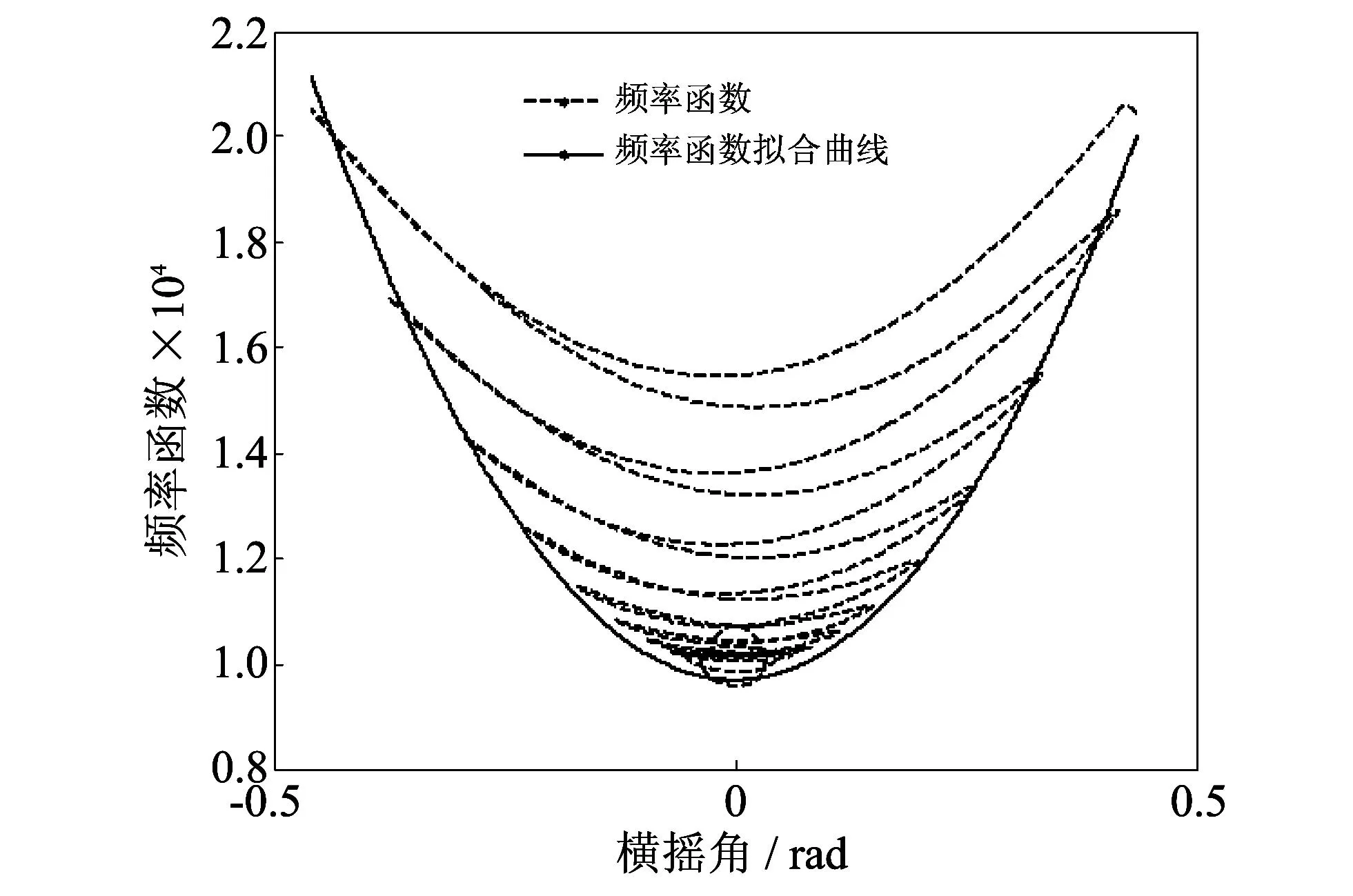
图 5 频率函数和拟合曲线Fig.5 Frequency function and fitted curve
估计出的阻尼项和恢复项系数d1, d2, k1和k3如表 1 所示. 由表 1 可知, 采用希尔伯特变换法和最小二乘拟合相结合可以快速有效地估计两栖车辆非线性横摇运动方程的系数, 最大估计参数的相对误差为0.313%.

表 1 参数估计结果表
将估计的系数代入式(1), 用四阶龙格库塔法求解, 与原系数的结果对比如图 6 所示.
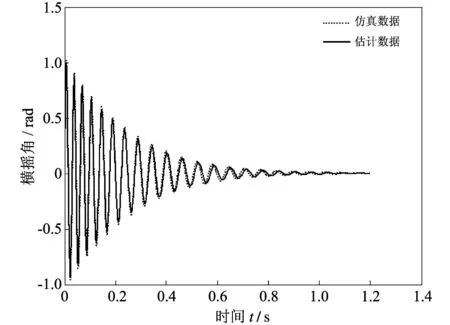
图 6 仿真和估计的衰减曲线Fig.6 Simulated decay curve and estimated decay curve
图 6 表明估计的角位移曲线与原数据的角位移曲线高度吻合. 因此可以证明用所提出估计非线性横摇运动方程的方法可行性, 精度满足工程需求.
需要特别指出, 上面仿真实例所生成的自由横摇衰减曲线是光滑的, 不含噪声, 因此估计的结果精度很高. 如果自由横摇衰减曲线包含噪声, 则精度会有所下降. 因此在使用该方法时, 必须先对测试所得的自由横摇信号进行滤波和平滑, 再应用本文提出的方法估计.
3希尔伯特变换法估计横摇运动方程参数
3.1两栖车辆自由横摇衰减实验
为了研究两栖车辆的非线性横摇运动, 根据某两栖车辆的技术参数, 设计了一个1∶4的缩小模型, 使其满足几何相似、 运动相似和动力相似, 如图 7 所示. 在试验水池里进行自由横摇衰减实验, 采样频率100Hz, 测得的自由横摇衰减曲线如图 8 所示.

图 7 两栖车辆拖模(1∶4)Fig.7 Scaled amphibious vehicle model(1∶4)
为了减小估计误差, 必须先对测试获取的自由横摇衰减曲线上的噪声进行滤波和平滑处理. 由图8可知, 前面和后面各有一段不规则的数据, 为了估计方便可以预先把自由横摇衰减曲线掐头去尾, 并认为起始时间为0, 以避免出现边界效应.

图 8 两栖车辆拖模自由横摇衰减曲线Fig.8 Test free rolling decay curve of amphibious vehicle model
在此基础上进行滤波, 滤波时分为两步. 第一步先用MATLAB里的butter函数设计一个Butterworth低通滤波器以去除高频噪声; 第二步进行小波分解重构法滤波, 小波基选择“rbio6.8”, 分解尺度为2; 最后选用三点平滑公式
(21)
进行数据平滑, 平滑后的自由横摇衰减曲线如图 9 所示.
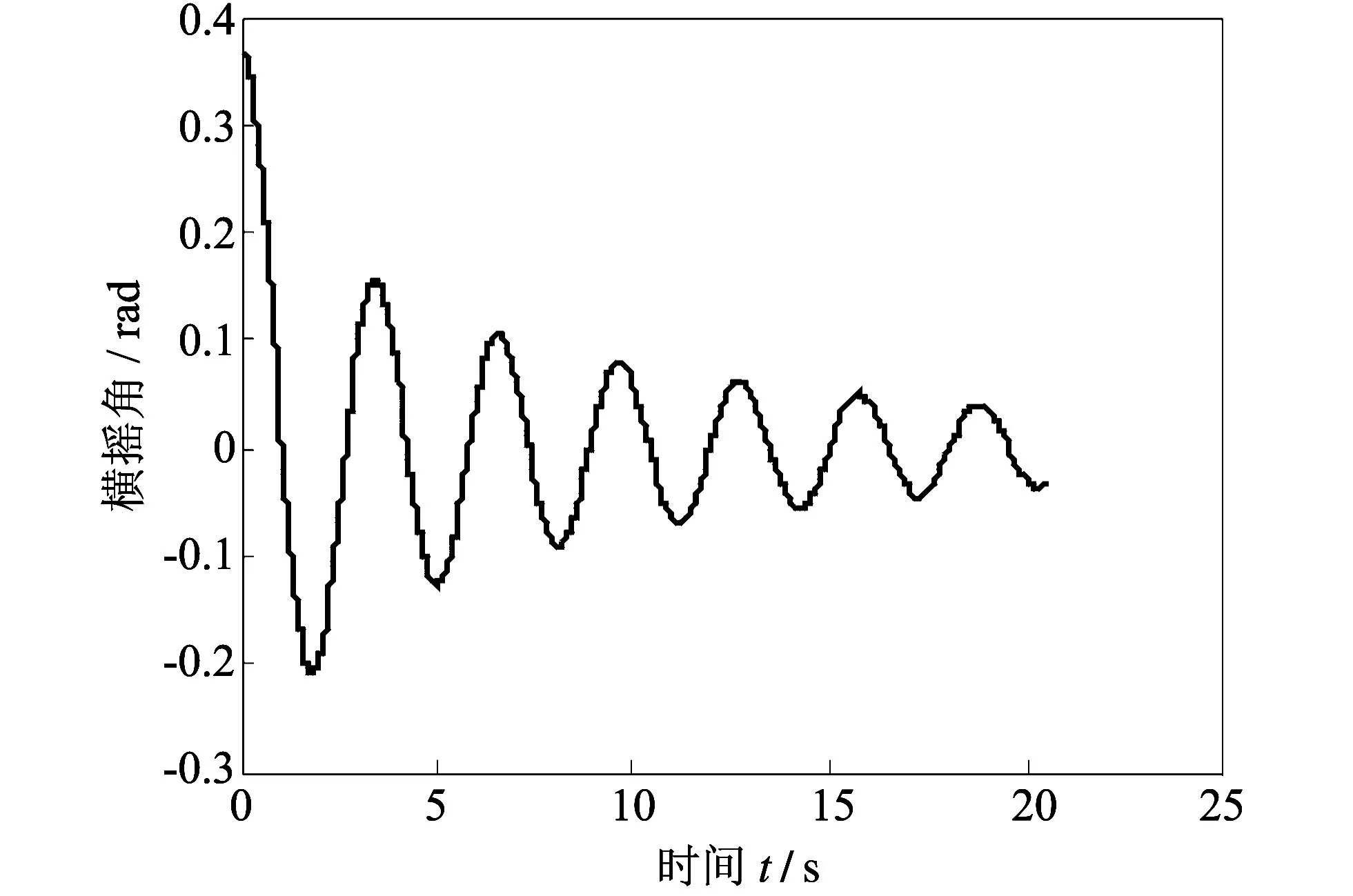
图 9 滤波后的自由横摇衰减曲线Fig.9 Free rolling decay curve after filter processing
3.2横摇运动参数估计
设两栖车辆非线性横摇的控制方程如方程(1)所示, 根据上述自由横摇衰减曲线估计d1, d2, k1和k3. 首先运用希尔伯特变换法把平滑后的自由横摇衰减曲线进行变换, 构造解析信号, 如图 10 所示.
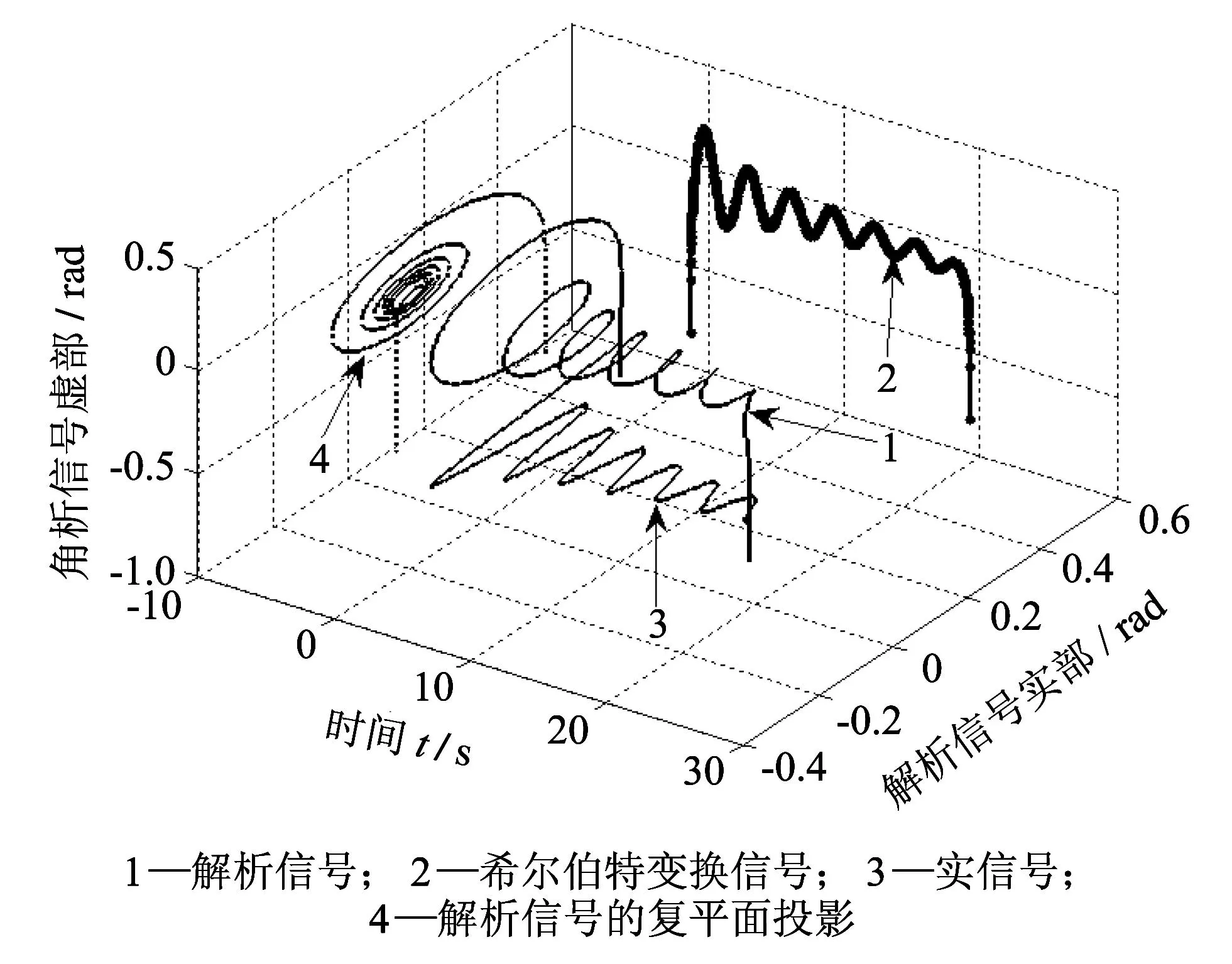
图 10 滤波后的横摇位移信号曲线Fig.10 Signal curve of roll motion after filter processing
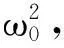


(22)
4估计结果与讨论

由图 11 可知, 估计横摇角度和测试的横摇角度吻合得较好. 与图 6 的对比结果可知, 该估计方法可以估计非线性横摇运动方程的参数, 但是对信号的噪声相应比较敏感, 因此要提高使用该方法估计非线性横摇参数的精度有两个途径:
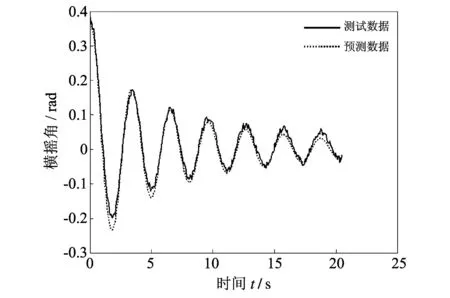
图 11 测试和估计的衰减曲线Fig.11 Measured decay curve and estimated decay curve
1) 提高测试系统的测试精度和信噪比, 使测试结果更准确.
2) 运用硬件和软件进行信号滤波, 并对测试信号进行平滑处理, 恢复理想的信号.
文献[1]中, 马新谋等采用能量法估计了两栖车辆的非线性阻尼系数, 用流体静力学理论计算了两栖车辆的GZ曲线, 并根据GZ曲线给了恢复项系数, 最终给出的两栖车辆非线性横摇运动方程为
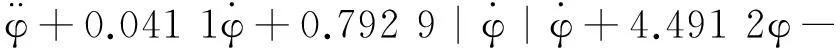

(23)
为了对比文献[1]和本文估计的非线性横摇方程的系数, 把它们列入表中, 如表 2 所示.

表 2 两种方法的参数估计结果
由表 2 可知, 两种方法获取的阻尼系数差距较大, 用能量法估计的阻尼值比希尔伯特法估计的小.GZ曲线拟合的线性恢复项系数和立方项恢复项系数的绝对值都比希尔伯特法估计的大, 但两个方法估计的非线性横摇运动方程都与实验数据吻合较好. 把文献[1]估计的非线性方程预测和本文预测的自由横摇衰减曲线和实验数据放在一起对比, 如图 12 所示.
由图 12 可知, 本文估计的固有频率相对于用GZ曲线法估计的固有频率而言更接近于试验数据. 分析原因是由于GZ曲线是根据设计图纸通过三维建模, 通过流体静力学计算出来的, 是图定数据, 为两栖车辆水上横摇运动的理论固有频率; 而本文估计的固有频率则是通过试验得到, 虽然该实验的拖模是满足几何相似、 运动相似和动力相似的, 但是不可避免地存在误差, 加之测试也存在噪声误差. 因此, 用希尔伯特变换法估计的非线性横摇运动从固有频率角度看更接近于实验值. 本文和文献[1]中仅用实验数据估计了阻尼项, 由图12可知, 本文估计的结果在幅值上更接近测试数据, 因而阻尼系数比文献[1]给出的结果大更符合测试结果. 从固有频率角度看误差比本文的大是正常的. 但是, 两种方法获得的固有频率非常接近, 无论用哪种方法来估计两栖车辆非线性横摇的恢复项都是可信的.

图 12 两种方法所得测试和估计的衰减曲线Fig.12 Measured decay curve and estimated decay curve by two methods
5结论
通过上述分析, 可以得出以下结论:
1) 希尔伯特变换法与最小二乘法相结合, 可以估计两栖车辆水上非线性横摇运动方程的系数.
2) 该方法不仅可以估计出阻尼项, 也可以估计出恢复项.
3) 该方法对测试信号的噪声敏感, 因此在使用该方法时必须先对自由横摇衰减试验信号进行滤波和平滑.
4) 该方法也可以用来估计船舶非线性横摇运动的模型, 也可以用来估计其他非线性动力学系统的模型.
参考文献:
[1]马新谋, 潘玉田, 常列珍. 两栖车辆非线性横摇阻尼系数估计[J]. 船舶力学, 2013, 17(5): 488-493.
MaXinmou,PanYutian,ChangLiezhen.Estimatednonlineardampingcoefficientsofamphibiousvehiclerollmotion[J].JournalofShipMechanics, 2013, 17(5): 488-493. (inChinese)
[2]马新谋, 常列珍, 侯宏花. 两栖车辆非线性横摇动力学参数辨识研究[J]. 中北大学学报(自然版), 2015, 36(2): 134-139.
MaXinmou,ChangLiezhen,HouHonghua.Aninvestigationondynamicparametersidentificationforamphibiousvehiclenonlinearrollmotion[J].JournalofNorthUniversityofChina(NaturalScienceEdition), 2015, 36(2): 134-139. (inChinese)
[3]徐国英, 薛劲橹. 两栖车辆在波浪中航行时的摇荡分析及解决方法[J]. 兵工学报, 2010, 31(5): 541-546.
XuGuoying,XueJinlu.Analysisandsolutionofamphibiousvehicle’stossmotioninwave[J].ActaArmamentarII, 2010, 31(5): 541-546. (inChinese)
[4]RobertsJB.Estimationofnonlinearshiprolldampingfromfree-decaydata[J].JournalofShipResearch, 1985, 29(2):127-138.
[5]ChakrabartiS.Empiricalcalculationofrolldampingforshipsandbarges[J].OceanEngineering, 2001, 28(7): 915-932.
[6]KimihikoU,NobuoK,KiyoshiA.Estimationofcoefficientsoftheequationofnonlinearrollmotionforfishingboatsbyimprovedenergymethodandgeneticalgorithm[J].JanpanJ.Indust.Appl.Math., 2003, 20: 155-192.
[7]JangTS,ChoiHS,HanSL.Anewmethodfordetectingnon-lineardampingandrestoringforcesinnon-linearoscillationsystemsfromtransientdata[J].InternationalJournalofNon-LinearMechanics, 2009, 44(7): 801-808.
[8]TaylanM.Theeffectofnonlineardampingandrestoringinshiproll[J].OceanEngineering, 2000, 27(9): 921-932.
[9]HouXR,ZouZJ.SVR-basedidentificationofnonlinearrollmotionequationforFPSOsinregularwaves[J].OceanEngineering, 2015, 109: 531-538.
[10]FeldmanM.Hilberttransforminvibrationanalysis[J].MechanicalSystemsandSignalProcessing, 2011, 25(3): 735- 802.
[11]FeldmanM.Hilberttransformmethodsfornonparametricidentificationofnonlineartimevaryingvibrationsystems[J].MechanicalSystemsandSignalProcessing, 2014, 47(3): 66 -77.
[12]ShinK,HammondJ.Fundamentalsofsignalprocessingforsoundandvibrationengineers[M].NewJersey:JohnWiley&Sons,Ltd., 2008.
[13]IgnacioG,RaidK.AnalysisoftheannualvariationsinthedynamicbehaviorofaballastedrailwaybridgeusingHilberttransform[J].EngineeringStructures, 2014, 60: 126-132.
[14]ShiZY,LawSS,XuX.Identificationoflineartime-varyingMDOFdynamicsystemsfromforcedexcitationusingHilberttransformandEMDmethod[J].JournalofSoundandVibration. 2009, 321(3-5): 572-589.
[15]KimY,ParkMJ.IdentificationofthenonlinearrolldampingandrestoringmomentofaFPSOusingHilberttransform[J].OceanEngineering. 2015, 109: 381-388.
文章编号:1673-3193(2016)04-0361-07
收稿日期:2016-03-31
基金项目:中北大学科学基金; 国防预研课题资助
作者简介:马新谋(1978-), 男, 博士, 讲师, 主要从事火炮自动武器与弹药工程的研究.
中图分类号:TJ811+.6
文献标识码:A
doi:10.3969/j.issn.1673-3193.2016.04.008
Identification for the Nonlinear Roll Motion Model ofAmphibiousVehicleUsingHilbertTransform
MA Xin-mou1, HAO Yi-ning1, CHANG Lie-zhen2, PAN Yu-tian1
(1. School of Mechatronics Engineering, North University of China, Taiyuan 030051, China;2.SchoolofScience,NorthUniversityofChina,Taiyuan030051,China)
Abstract:To identify the coefficients of nonlinear roll motion modelling of amphibious vehicle, the Hilbert Transform (HT) method is applied for a free roll decay signal in time domain to obtain an analytical signal. The analytical signal provides information on the instantaneous amplitude and instantaneous frequency. Then, the relationship between the instantaneous amplitude/frequency and the nonlinear parameters can be derived. Least square method is used to estimate unknown parameters of nonlinear roll motion of amphibious vehicle. The present method is applied to a numerical experiment data and then to real free roll decay data obtained from a 1∶4 scale model of an amphibious vehicle to identify nonlinear parameters. The obtained nonlinear damping coefficients and nonlinear restoring coefficients are good agreement with the true value and tested data. So, the present method can be used to identify nonlinear roll motion equation of amphibious vehicle with enough accuracy.
Key words:Hilbert transform method; amphibious vehicle; nonlinear roll motion; envelope; instantaneous frequency

