行进间装填对输弹机设计的影响

薛百文， 阮伟靖， 崔建春

(1. 中北大学 机电工程学院， 山西 太原 030051； 2. 中北大学 计算机与控制工程学院， 山西 太原 030051)



行进间装填对输弹机设计的影响

薛百文1， 阮伟靖1， 崔建春2

(1. 中北大学 机电工程学院， 山西 太原 030051； 2. 中北大学 计算机与控制工程学院， 山西 太原 030051)

摘要:自行火炮在行进间输弹时， 弹丸在惯性输弹段会受到底盘运动状态的影响. 根据相关路面谱数据， 分析了自行火炮颠簸运动时弹丸的受力， 建立了惯性输弹段弹丸的运动方程， 通过实例计算， 得到了极限状态下输弹到位所需要的输弹速度曲线. 研究结果对输弹机设计具有一定的参考意义.

关键词:行进间装填； 惯性输弹； 强制输弹； 输弹机； 路面谱

0引言

现代战争中出现了自行火炮， 它需要在行进间进行装填与发射[1-3]， 这对火炮的自动装填机构提出了更高的要求. 德国生产的155mm榴弹炮较早地实现了行进间装填与发射. 现代火炮在输弹的全行程上， 分为强制输弹与惯性输弹两个阶段[4]. 其原理如图 1 所示， 强制输弹阶段， 弹丸受到外力的作用， 加速前进. 在图中Lqz段行程结束后， 弹丸达到一定速度， 进入惯性输弹阶段， 依靠惯性运动. 不再受强制作用力. 故自行火炮底盘的运动状态会影响弹丸的运动， 甚至影响弹丸装填的到位情况.

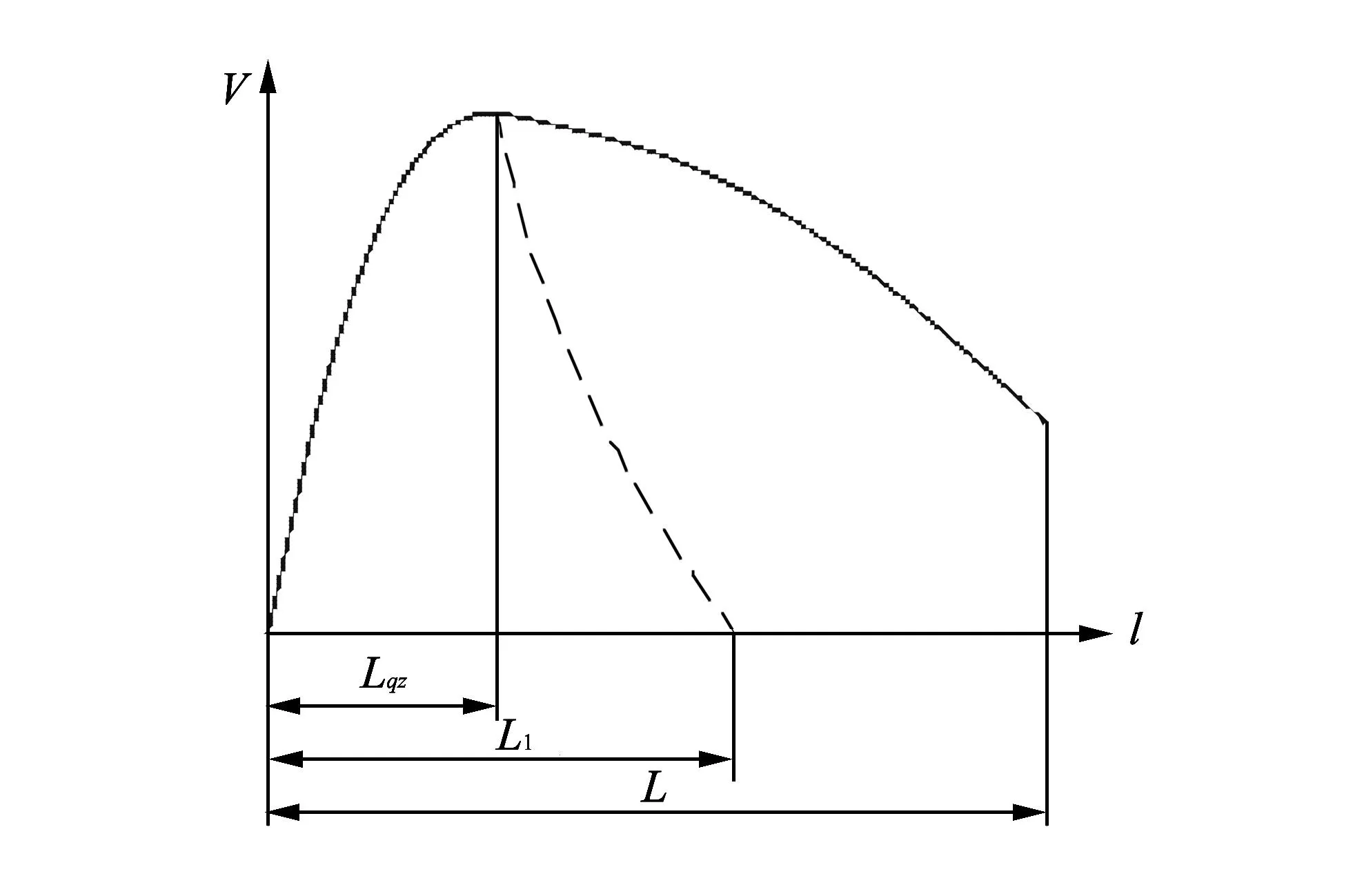
图 1　火炮输弹机原理示意图Fig.1　Principle diagram of artillery ramming machine

1惯性输弹段弹丸运动方程的建立

1.1惯性输弹段弹丸的受力分析

从理论上讲， 惯性输弹段弹丸不受力(忽略弹丸托盘的支承力). 由于受到运动中的底盘的影响， 惯性输弹段的弹丸的受力如图 2 所示. 图中θmax为车体摆动的最大角度， αmax为最大射角， R为车体摆动时的回转半径， Fq弹丸的重力， Ft为由车体摆动引起的惯性力沿弹丸运动方向的分力； Fr为该惯性力在与弹丸运动方向相垂直方向的分力.

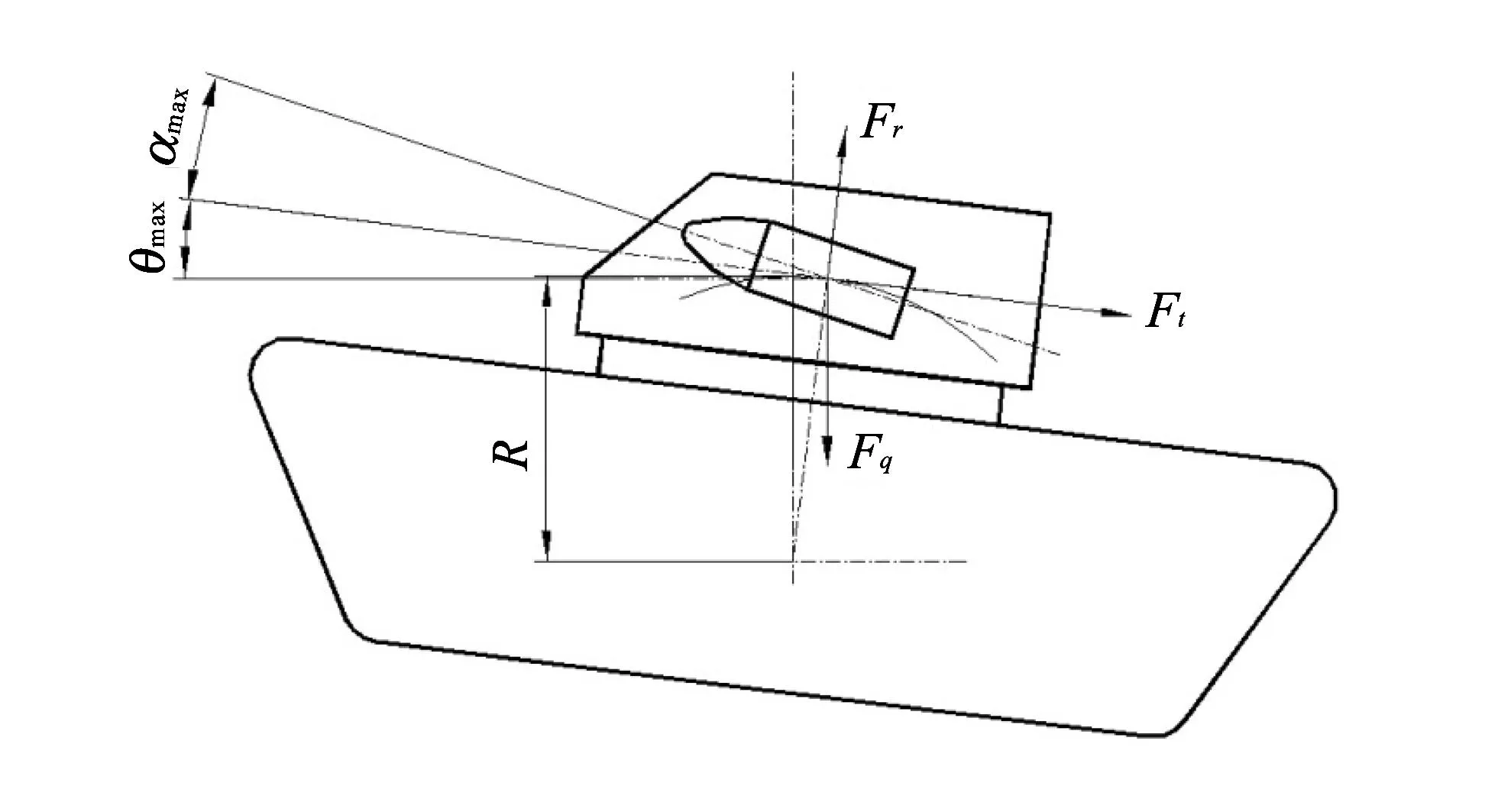
图 2　火炮行进间惯性输弹段弹丸受力示意图Fig.2　Forces analysis of projectile in inertia ramming stage for moving artillery

1.2运动方程的初步建立

通过以上对弹丸在输弹惯性段的受力分析， 可以建立惯性输弹段弹丸的运动方程为

(1)

式中：m为弹丸质量；v为弹丸在惯性输弹行程上的瞬时速度； Fq为弹丸所受的重力； Ft为车体颠簸引起的惯性力的切向分力； Fr为惯性力的法向分力.

由于式(1)较为复杂， 不能积分. 但是装填过程是一个为时极短的过程， 可假设弹丸的运动是在自行火炮的倾斜角为某个固定值不变的状态下发生的. 同时， 认为全炮仅在瞬间处于该点， 即由于路面不平引起的全炮颠簸而产生的惯性力对于运动着的弹丸是起作用的. 那么应对运动着的全炮在路面上可能形成的最大倾斜角的情况进行计算.

1.3火炮行进间车体倾角变化计算

1.3.1总体变化规律

火炮在运动中的颠簸可能是左右的， 也可能是前后的. 左右颠簸时， 由于弹丸受托弹盘槽的约束， 所以它对弹丸的影响不大. 在此不予考虑. 只考虑前后颠簸的情况. 这时倾角的变化规律参考某舰炮设计讲义按式(2)计算.

(2)

式中：θ为倾斜角的瞬时值；t为时间的瞬时值；θmax为颠簸运动引起的车体倾斜角的最大值， rad；T为颠簸运动的周期.

故可得颠簸运动的角速度为

(3)

可得颠簸运动的角加速度为

(4)

1.3.2倾角最大值与变化周期的确定

路面不平度具有随机性, 在地面波形的随机分析中常假定过程是平稳、 遍历且呈正态分布. 为了在计算机上模拟随机路谱,文献[5]设计了一个随机数产生器, 它可产生服从正态分布. 文献[4] 则对路面谱选取实测标准正弦路面谱. 其路面质量相关的参数中波长为1 800 mm， 总幅值为110 mm[6]. 另选取火炮运动速度为V=30 km/h. 可得：火炮在行进间的颠簸运动的周期T=0.216 s，θmax=0.121 6 rad.

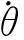
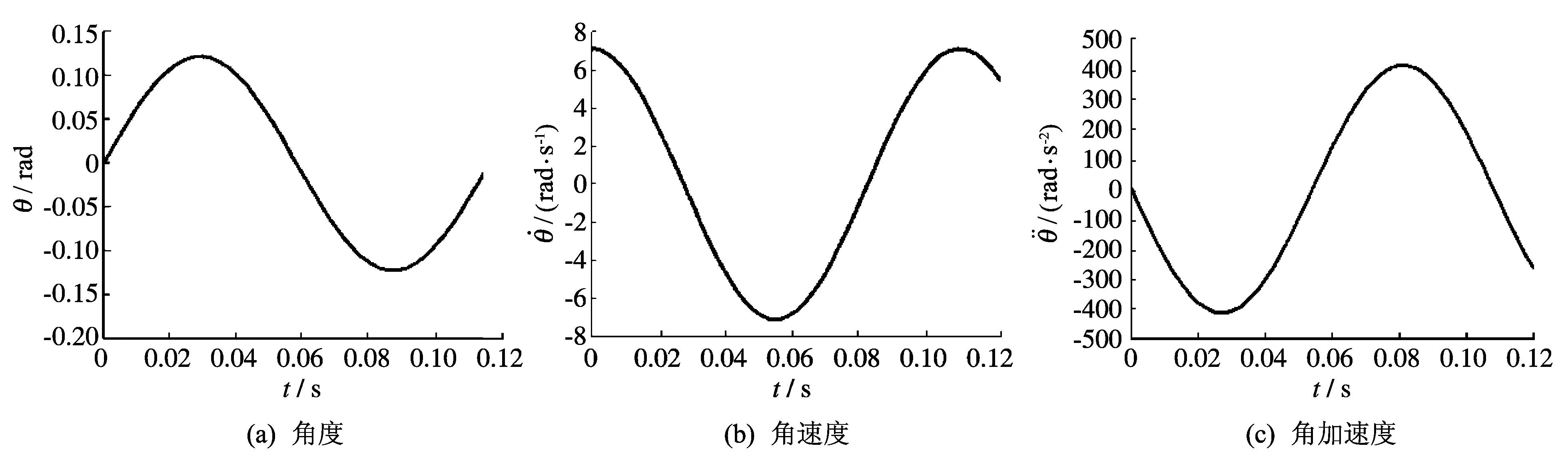
图 3　行进间火炮倾斜角参数随时间的变化Fig.3　Change of tilt angle parameter with time for moving artillery

1.3.3附加惯性力计算

因颠簸产生的惯性力的值， 可由理论力学的相关知识计算得到[7].

(5)

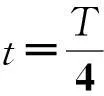
这时， 弹丸的运动方程为

1.4运动方程的建立

因为弹丸运动沿直线进行， 其运动方程式可以投影到运动方向上， 则

(6)

式中：R为火炮的质心到弹丸质心的距离；f为弹丸与输弹槽之间的摩擦系数.

将式(6)进行化简， 可得

(7)

将式(7)左边在速度v0-v1上积分， 右边在弹丸行程Lqz-L上积分， 可得

(8)

式中：v0是强制输弹结束时弹丸的速度；v1是输弹到位时弹丸的速度；L为输弹的全行程.

用字母A表示式(8)中的常数项， 用Lgx表示(L-Lqz)， 则可将式(8)表示为

(9)

2算法举例

某122 mm榴弹炮的实际参考数据为：m=21.76 kg，αmax=70°，αmin=-7°，R=2 100 mm，f=0.15，Lgx=0.6 m， 如果输弹到位的速度为v1=1.5 m/s[8-9].

将这些数值代入式(9)， 可得

403.2

当考虑火炮行进间颠簸时， 为保证输弹到位时的速度， 强制输弹末期， 弹丸速度为

15.63m/s.

如果不考虑火炮行进间的颠簸， 则参数A的值为

A70°=19.43.

则强制输弹末期弹丸速度为

3.73 m/s.

同理可得：A-7°=-114. 图 4 为参数A随火炮射角的变化情况， 图 5 为考虑颠簸时强制输弹末期弹丸速度随射角的变化情况， 这一计算结果表明：在惯性输弹行程上， 由于重力的作用， 弹丸速度将越来越快， 不能保证弹丸的安全， 因此， 在行进间最好不要在小射角状态下装填弹丸.

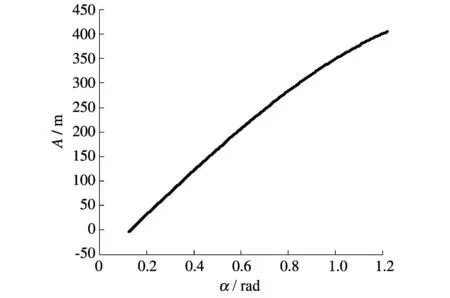
图 4　参数A随火炮射角α的变化Fig.4　Change of parameter A with fire angle

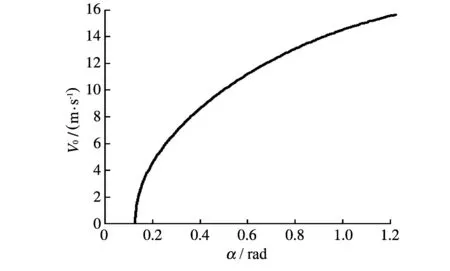
图 5　底盘颠簸时v0随射角的变化Fig.5　Change of parameter v0 with fire angle at condition of dumped chassis

3结论

1) 自行火炮在静止状态进行弹丸装填及射击， 其强制输弹段末期弹丸的速度在任何射角下变化不大.

2) 自行火炮在行进间进行射击， 必然涉及到行进间输弹. 火炮底盘的运动状态将对弹丸能否正常装填产生较大影响. 从上述的分析知， 火炮运动速度及地面谱对惯性输弹段的弹丸影响较大.

3) 火炮在一定的路面上以一定速度行走， 这时为保证弹丸装填到位的速度， 随着射角的变化， 强制输弹段末期， 弹丸所需的速度值变化较大.

4) 考虑到现代火炮必然存在行进间输弹与射击的情况， 故在输弹机设计时， 其输出速度应有较大变化范围.

参考文献：

[1]霍建鹏. 绝对火力—PzH2000式155毫米自行榴弹炮[M]. 北京：兵器工业出版社， 2012.

[2]仁立. 德国PzH2000自行榴弹炮[J]. 现代兵器， 2001(10)：18-22.

RenLi.SelfpropelledartilleryPZH2000madeinGermany[J].ModernOrdance, 2001(10)：18-22. (inChinese)

[3]郭竞尧， 谢杨杨， 张永涛. 同旋向供弹单元设计与仿真优化[J]. 火炮发射与控制学报， 2015(1)：25-28.

GuoJingyao，XieYangyang，ZhangYongtao.Designandsimulatingoptimizationofammunitionfeedingunitwithsamerotatingdirection[J].JournalofGunLaunch&Control, 2015(1)：25-28. (inChinese)

[4]谈乐斌， 张相炎， 管红根, 等. 火炮概论[M]. 北京：北京理工大学出版社， 2005.

[5]闵建平， 杨国来， 王长武, 等. 行进间发射平顺性研究[J].南京理工大学学报， 2000， 24(4)：327-329.

MinJianping，YangGuolai，WangChangwu,etal.Ridecharacteristicsofself-propelledgunsatfiringduringtravelling[J].JournalofNanjingUniversityofScienceandTechnology, 2000， 24(4)：327-329. (inChinese)

[6]李军， 张洪康， 孟红, 等. 履带车辆行驶平顺性仿真分析研究[J]. 车辆与动力技术， 2003(4)：4-7.

LiJun,ZhangHongkang,MengHong,etal.Researchoftrackedvehiclecompliancesimulation[J].Vehicle&PowerTechnology, 2003(4): 4-7. (inChinese)

[7]王月梅， 曹咏弘. 理论力学[M].北京：机械工业出版社， 2010.

[8]席栓寿. 膛线类型对火炮身管寿命的影响[J].四川兵工学报， 1992， 47(4)：73-78.

XiShuanshou.Theinfluenceofrifletypesonguntubeslifespan[J].JournalofSichuanOrdnance, 1992， 47(4)：73-78. (inChinese)

[9]张相炎. 火炮自动机设计[M]. 北京：北京理工大学出版社， 2010.

文章编号：1673-3193(2016)04-0391-04

收稿日期：2015-05-22

作者简介：薛百文(1966-)， 男， 副教授， 硕士， 主要从事火炮设计与制造工艺研究.

中图分类号:TJ302

文献标识码:A

doi:10.3969/j.issn.1673-3193.2016.04.013

Influence of Moving Loading on Design ofRammingMachine

XUE Bai-wen1， RUAN Wei-jing1， CUI Jian-chun2

(1. School of Mechatronics Engineering， North University of China， Taiyuan 030051, China;2.SchoolofComputerScienceandControlEngineering，NorthUniversityofChina，Taiyuan030051，China)

Abstract:The inertia ramming of projectile was affected by the motion state of chassis when self propelled artillery was moving. Based on the relevant road surface spectrum, forces acting on the projectile were analyzed when self propelled artillery dumps on the road, and motion equations of projectile in inertia ramming stage was established. The ramming speed curve was obtained by calculating an example when projectile was rammed to proper place in dumped limit state. The results are available for designing the ramming machine.

Key words:moving loading； inertia ramming； forced ramming； ramming machine； road spectrum