开孔方形防沉板在海底黏性土中的承载特性
张所辉 吴姝娜 金涛

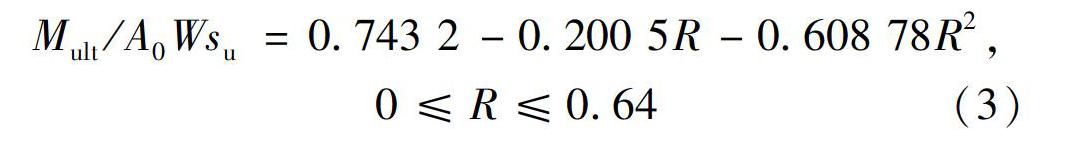
摘要:为探究海洋基础工程中开孔防沉板地基的承载力和稳定性,在Abaqus中建立不同开孔率的开孔防沉板与不排水饱和黏性土体的相互作用模型,模拟单向和复合加载作用下地基的破坏过程,研究防沉板开孔率与地基承载力的相互关系。研究结果可为实际工程中给定载荷下方形开孔防沉板结构的快速设计、承载力校核和稳定性判断提供参考。
关键词:
海洋基础工程; 防沉板; 位移控制法; 承载力; 归一化; 包络线
中图分类号:P754.5;TP391.99
文献标志码:B
Bearing capacity of square perforated mudmat on seabed soft clay
ZHANG Suohui, WU Shuna, JIN Tao
(Institute of Process Equipment, Zhejiang University, Hangzhou 310027, China)
Abstract:
To study the bearing capacity and stability of the foundation with perforated mudmat in the ocean foundation engineering, the model of interaction between perforated mudmat with different opening ratio and undrained saturated seabed soft clay is established in Abaqus. The relationship between the opening ratio of the mudmat and the bearing capacity of the foundation is studied. The results can provide reference for the rapid design, bearing capacity check and stability judgment of the square perforated mudmat structure under the given load in actual project.
Key words:
ocean foundation engineering; mudmat; displacement control method; bearing capacity; normalization; envelope
0 引 言
防沉板是水下生产系统的一种浅基础形式,广泛用于支撑各种海底结构。但是,在一些情况下,要承载的设备较大,所需的防沉板过大过沉,不便于运输和安装,因此对其结构进行优化,出现开孔防沉板。开孔防沉板的优势是可以提高材料利用率、节省成本,便于运输和安装,方便迁移、回收和重复使用。[1]
国内对开孔防沉板的研究较少,近几年只有一些国外学者对开孔防沉板上拔承载力和竖向承载力进行相关研究。本文以方形开孔防沉板基础为研究对象,采用有限元方法系统研究其地基承载力和稳定性,为海洋基础工程施工的防沉板结构和主要尺寸快速设计提供参考。
1 有限元模型建立和分析方法
Abaqus软件在分析非线性问题上具有明显优势,因此本文数值分析均采用Abaqus软件。
1.1 有限元模型的建立
方形防沉板模型见图1。防沉板厚度为0.04 m,具体尺寸见表1。为便于后续分析,防沉板的宽度用B表示,孔的宽度用a表示,开孔率用R表示。方形防沉板 土体有限元模型见图2。
防沉板材料为钢,采用理想弹塑性本构模型,假定其放置在不排水饱和黏土地基上,黏土的力学行为采用基于Tresca屈服准则的线弹性理想塑性本构模型。[2 3]防沉板放置在与土体可分离的无拉力接触面上。为数据提取和分析的需要,设置参考点P、竖向载荷、水平载荷、弯矩载荷和扭矩载荷等,所涉及的变量符号及含义见表2,载荷的方向示意见图3。
1.2 数值分析方法
在复合加载模式的地基承载力分析中,通常采用位移控制法进行加载。位移控制模式主要分为Swipe加载模式[4]和Probe固定位移比加载模式[5]。
综合考虑计算效率和准确性,V H、V M和V T载荷空间内的承载力包络线采用Swipe加载法,其余的承载力包络线选用Probe加载法。
2 单向加载模式下的极限承载力
2.1 竖向极限承载力
对防沉板施加竖向位移,提取参考点反力,得到不同开孔率方形防沉板地基的竖向载荷随位移的变化曲线,见图4。
由此可知,随着开孔率的增大,地基的竖向极限承载力逐渐降低。定义形状系数sc,方形开孔防沉板地基的竖向极限承载力Vult=suNcA0sc,其中:su为土体的剪切强度;Nc为条形基础的竖向承载力因数,取5.14;A0为R=0的方形防沉板地基的面积。形状系数sc与开孔率R的关系见图5。
由此可以看出,开孔防沉板的形状系数sc与开孔率近似呈线性关系,通过最小二乘法拟合得到其表达式为
sc=1.177 42-1.171 90R, 0≤R≤0.64
(1)
2.2 水平極限承载力
对防沉板施加水平位移,提取参考点反力,得到不同开孔率方形防沉板地基水平载荷随位移的变化曲线,见图6。
由此可知,随着水平位移的增大,水平载荷先线性增大,然后当位移增大超过某一值后载荷基本保持不变,即达到极限平衡状态。开孔率与地基水平极限承载力的无量纲值Hult/A0su关系见图7。
由图7可知,Hult/A0su随开孔率增大呈线性减小,在0≤R≤0.64时二者的拟合关系为
HultA0su=1.142 56-0.889 17R
(2)
2.3 极限抗倾覆承载力
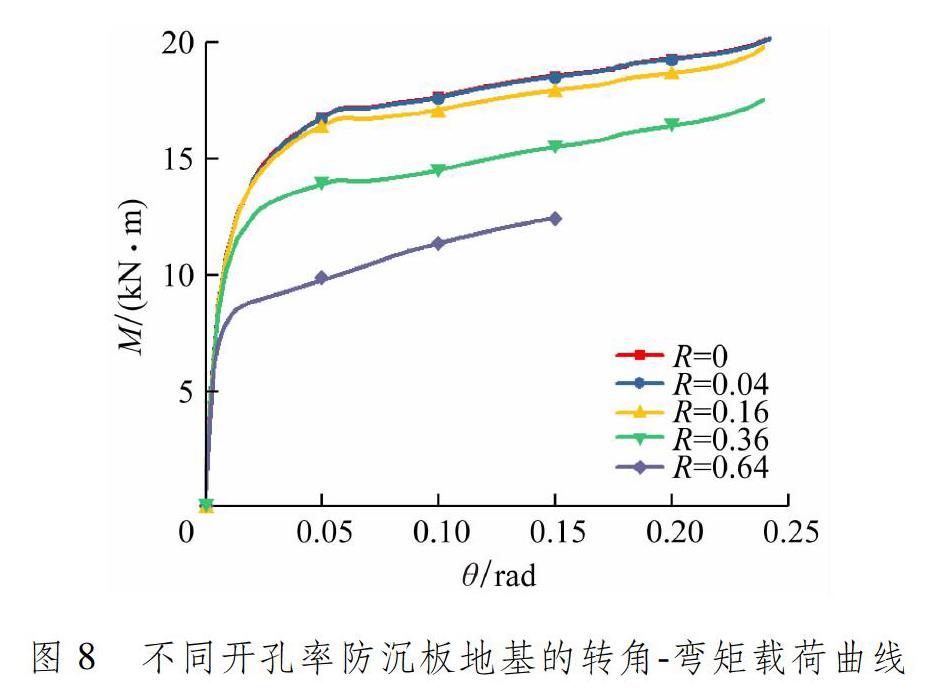
对防沉板施加转角,提取参考点反力,得到不同开孔率方形防沉板地基的弯矩载荷随转角的变化曲线,见图8。
由此可知:在达到极限弯矩载荷后,地基的弯矩载荷仍然随转角增大缓慢增大;在开孔率为0和0.04时,2条曲线基本重合,说明当开孔率较小时,开孔率对地基抗弯承载性能的影响较小。
防沉板地基的抗倾覆极限承载力的无量纲值Mult/A0Wsu(W为地基模型的宽度)与开孔率R的关系见图9。拟合数据得到开孔防沉板地基抗倾覆极限承载力与开孔率的关系式为
Mult/A0Wsu=0.743 2-0.200 5R-0.608 78R2,
0≤R≤0.64
(3)
2.4 极限抗扭承载力
不同开孔率方形防沉板地基的扭矩载荷与转角关系曲线见图10。由此可知:开孔率为0和0.04的2条曲线基本重合,当开孔率为0.16时抗扭极限承载力稍有减小,说明当防沉板的开孔率较小时,开孔率对地基抗扭承载性能的影响较小。
防沉板地基的抗扭极限承载力无量纲值Tult/A0Wsu与开孔率R之间的关系见图11。拟合图中数据点,得到开孔防沉板地基的抗扭极限承载力与开孔率的关系为
TultA0Wsu=0.306 71-0.003 93R-0.254 69R2,
0≤R≤0.64
(4)
3 在复合载荷作用下的地基承载力包络线
3.1 在竖向载荷作用下二维载荷空间的地基承载力包络线
3.1.1 V H载荷空间内的地基承载力包络线
当弯矩载荷M=0、扭矩载荷T=0时,模拟得到V H载荷空间内不同开孔率的防沉板地基承载力包络线,见图12。采用前文得到的单向极限承载力,对包络线进行归一化处理,并与GREEN[6]和FENG等[7]的结果进行对比,见图13。
由图12和13可知,随着开孔率的增大,归一化的地基承载力包络线有外扩的趋势,但变化趋势总体上基本相似。与GREEN[6]和FENG等[7]的结果对比可以看出,有限元数值计算得到的不同开孔率防沉板归一化的承载力包络线基本都落在FENG等[7]的结果外侧,且与开孔率为0的承载力包络线吻合较好。对FENG等[7]提出的公式稍作修改,得到开孔率为0的开孔方形防沉板在V H载荷空间内的承载力包络线下限的公式为
v=0.4+0.61-h1.6
(5)
当v≤0.4时,h=1。
3.1.2 V M载荷空间内的地基承载力包络线
当水平载荷H=0、扭矩载荷T=0时,模拟得到在V M载荷空间内不同开孔率防沉板地基的承载力包络线,见图14。对包络线进行归一化处理,并与GOURVENEC[8]的結果进行对比,见图15。
由图14可知:当地基所能承受的极限弯矩载荷达到最大值后不再增大,此时对应的竖直方向的载荷约为单向竖直极限承载力的1/2。由图15可知:地基承载力包络线大致关于V=0.5Vult对称;当开孔率较小时,承载力包络线与GOURVENEC[8]的结果吻合较好;随着开孔率的增大,V M载荷空间内归一化的地基承载力包络线有向内收缩的趋势,并逐渐向m=-2v+2靠近。
3.1.3 V T载荷空间内的地基承载力包络线
水平载荷H=0、弯矩载荷M=0时,模拟得到V T载荷空间内不同开孔率防沉板地基的承载力包络线,见图16。
由图16可知,V T载荷空间内的承载力包络线与V H载荷空间内的承载力包络线具有相似的形状,两者的地基破坏模式相似。将地基承载力进行归一化处理,并与ABYANEH等[9]和FENG等[7]的结果进行对比,见图17。
由图16和17可知:随着开孔率增大,开孔防沉板地基的承载性能逐渐降低,归一化的承载力包络线逐渐向内收缩,但变化趋势总体上基本相似;开孔率为0的方形防沉板地基的有限元数值计算结果与ABYANEH等[9]的结果较吻合。
3.2 V H M三维载荷空间地基承载力包络面
为分析方便,将V H M三维空间的地基承载力包络面投影到H M载荷空间,对比不同竖向载荷下H M空间的地基承载力包络线。初始时刻,在基础
参考点上分别施加V=0.25Vult、V=0.50Vult和
V=0.75Vult的竖向载荷,进行数值模拟并进行归一化处理,与GOURVENEC[8]和申志超[10]的结果进行对比,得到3种竖向载荷作用下不同开孔率防沉板的H M载荷空间地基承载力包络线,见图18。
由图18可知,不同竖向载荷作用下的H M载荷空间地基承载力包络线具有非对称性,且随着开孔率的增大,包络线对称性逐渐增强。对GOURVENEC[8]的公式进行调整,给出v≤0.50和v=0.75时开孔防沉板在V H M载荷空间内的稳定性判断公式分别为
3.3 双轴水平和力矩载荷下的地基承载力包络线
3.3.1 Hx Hy载荷空间的地基承载力包络线
任意方向的水平极限载荷Hult都能分解为沿x轴和y轴2个方向的水平载荷Hx和Hy,故研究Hx和Hy成0°、30°、45°、60°和90°时地基的水平极限承载力,得到任意方向水平载荷作用下不同开孔率防沉板地基的承载力包络线,见图19。在Hx Hy载荷空间内不同开孔率防沉板地基归一化的承载力包络线与FENG等[7]的结果对比见图20。
由图20可以明显看出,开孔防沉板地基Hx Hy载荷空间内的承载力包络线形状与开孔率无关,并且归一化后不同Hx/Hy对应的水平极限承载力的点均落在FENG等[7]给出的曲线上。
3.3.2 Mx My载荷空间的地基承载力包络线
开孔防沉板可能受到偏心的竖向载荷,导致弯矩载荷的方向是任意的。由第3.1.2节可知,在无拉力接触面上,地基的抗弯极限承载力出现在V=0.50Vult附近,因此,先给防沉板施加V=0.50Vult的竖向载荷并保持不变,研究0°、30°、45°、60°和90°方向弯矩载荷作用下的承载力包络线,见图21。
对该承载力包络线进行归一化处理,并与GREEN[6]、申志超[10]和刘润等[11]的研究结果进行对比,见圖22。
由图22可知:当开孔率为0时,承载力包络线落在刘润等[11]和申志超[10]的结果之间;随着开孔率的增大,Mx My载荷空间内承载力包络线逐渐向内收缩。调整申志超[10]的公式,给出开孔率为0和0.64的防沉板地基在Mx My载荷空间的承载力包络线公式分别为
3.4 扭矩载荷作用下二维载荷空间的地基承载力包络线
3.4.1 T H载荷空间的地基承载力包络线
讨论扭转载荷对不同开孔率防沉板地基抗滑特性的影响时,因模型的长宽相等,故只研究T Hx载荷空间(V=M=0)内地基的承载力包络线,见图23。对该包络线进行归一化处理,并将结果与FENG[12]和FINNIE等[13]的关系式进行对比,结果见图24。
由此可知:开孔率为0的方形防沉板的承载力包络线形状与前人的结果较吻合;随着开孔率的增大,T Hx载荷空间的承载力包络线逐渐向内收缩,但变化趋势总体上基本相似。
3.4.2 T M载荷空间的地基承载力包络线
在竖直载荷V=0.50Vult时,地基的极限抗弯承载力最大。因为防沉板地基的长和宽相等,所以只研究T Mx载荷空间内地基的承载力包络线,不同开孔率的方形开孔防沉板地基在T Mx载荷空间内的承载力包络线见图25。
由于防沉板放置在无拉力接触面上,在弯矩载荷作用下防沉板会脱离地基,使得其抗扭载荷逐渐减小。随着开孔率的增大,在弯矩和扭矩载荷的共同作用下,方形防沉板地基的承载性能逐渐降低。进行归一化处理后,与申志超[10]提出的公式进行对比,结果见图26。
当防沉板不开孔时,在T Mx载荷空间内防沉板承载力包络线与申志超[10]提出的公式吻合较好;随着开孔率的增大,T Mx载荷空间的包络线包络线逐渐向内收缩,但各归一化包络线形状总体上相似。
4 结束语
利用有限元软件Abaqus,对不排水饱和黏土上单向和复合加载作用下防沉板地基的破坏过程进行模拟,研究防沉板开孔率与地基承载力的相互关系。为实际工程中给定载荷下方形开孔防沉板结构的快速设计、承载力校核和稳定性判断提供依据。
参考文献:
[1] WHITE D J, MACONOCHIE A J, CHEUK CY, et al. An investigation into vertical bearing capacity of perforated mudmats[C]// Proceedings of International Symposium Frontiers in Offshore Geotechnics(IS FOG 2005). Perth: ACADEMIA, 2005: 459 465. DOI: 10.1201/NOE0415390637.ch47.
[2] GOURVENEC S. Effect of embedment on undrained capacity of shallow foundations under general loading[J]. Géotechnique, 2008, 58(3): 177 185. DOI: 10.1680/geot.2008.58.3.177.
[3] XIAO Z, TIAN Y, GOURVENEC S. A practical method to evaluate failure envelopes of shallow foundations considering soil strain softening and rate effects[J]. Applied Ocean Research, 2016, 59: 395 407. DOI: 10.1016/j.apor.2016.06.015.
[4] GOURVENEC S, BARNETT S. Undrained failure envelope for skirted foundations under general loading[J]. Géotechnique, 2011, 61(3): 263 270. DOI: 10.1680/geot.9.T.027.
[5] BRANSBY F, RANDOLPH M. Effect of embedment depth on undrained response of skirted foundations to combined loading[J]. Soil and Foundations, 1999, 39(4): 19 33. DOI: 10.3208/sandf.39.4_19.
[6] GREEN A P. Plastic yielding of metal junctions due to combined shear and pressure[J]. Journal of Mechanics and Physics of Solids, 1954, 2(3): 197 211. DOI: 10.1016/0022 5096(54)90025 3.
[7] FENG X, RANDOLPH M F, GOURVENEC S, et al. Design approach for rectangular mudmats under fully three dimensional loading[J]. Géotechnique, 2014, 64(1): 51 63. DOI: 10.1680/geot.13.P.051.
[8] GOURVENEC S. Shape effects on capacity of rectangular footings under general loading[J]. Géotechnique, 2007, 57(8): 637 646. DOI: 10.1680/geot.2007.5.8.637.
[9] ABYANEH S D, OJO A, MACONOCHIE A, et al. Undrained bearing capacity of shallow foundations subjected to three dimensional loading including torsion[C]// Proceedings of 25th International Ocean and Polar Engineering Conference. Kona: International Society of Offshore and Polar Engineers, 2015: 668 673.
[10] 申志超. 離岸浅基础在复合加载模式下的承载力特性研究[D]. 天津: 天津大学, 2016.
[11] 刘润, 刘孟孟, 杨树耕. 饱和软黏土中不同形状深水防沉板基础承载特性研究[J]. 海洋学报, 2016, 38(3): 131 144. DOI: 10.3969/j.issn.0253 4193.2016.03.013
[12] FENG X, RANDOLPH M F, GOURVENEC S. An analytical solution for undrained horizontal torsional resistance of mudmats[J]. Géotechnique, 2016, 67(4): 325 337. DOI: 10.1680/jgeot.16.P.026.
[13] FINNIE I M S, MORGAN N. Torsional loading of subsea structures[C]// Proceedings of 4th International Offshore and Polar Engineering Conference. Toulon, 2004: 326 333.
(编辑 武晓英)

