基于问题驱动的数学期望定义的教学探讨

李新娜，陈　轲

(1.信息工程大学 理学院,河南 郑州 450002；2.信息工程大学 导航与空天目标工程学院,河南 郑州450002)



基于问题驱动的数学期望定义的教学探讨

李新娜1，陈轲2

(1.信息工程大学 理学院,河南 郑州 450002；2.信息工程大学 导航与空天目标工程学院,河南 郑州450002)

摘要：以问题为驱动，数学期望定义的教学划分为“离散型随机变量的数学期望的定义”、“数学期望的含义”、“连续型随机变量的数学期望的定义”和“数学期望的应用”4个层次.

关键词：数学期望;问题驱动;离散;连续

0引言

数字特征能够描述随机变量或人们较关心的某些方面的重要特征，在理论上和应用中都非常重要.尤其数学期望是其他数字特征的基础，因此在教学过程中需要给予“数学期望”更多的关注.然而，在常见的概率论与数理统计教材[1-2]里，数学期望的引入是通过介绍离散型随机变量按各种取值的概率大小所作的加权平均值进行解释的，而对于连续型随机变量的数学期望则直接给出数学定义，使得学生很难对数学期望的概念获得较深刻的认识[3].

鉴于此，作者以问题为驱动，将数学期望定义的教学划分4个层次.首先，从简单的生活实际问题出发，通过组织学生讨论，让学生在讨论中感受引入数学期望概念的必要性，再逐步引导学生推导和总结出离散型随机变量数学期望的定义;其次，通过对离散型随机变量数学期望的公式演化，清晰地看出数学期望的含义，进而，对连续型随机变量进行离散化,自然地导出连续型随机变量数学期望的定义；最后，通过对美国数学竞赛评分标准的探讨，引发学生层层思考来推动知识点的展开，引导学生利用现有知识解决实际问题.

1离散型随机变量的数学期望的定义

通过引例分析，结合总结求解过程，引入离散型随机变量的数学期望的定义.

引例评判打靶水平.甲、乙两个射手打靶，其命中环数X，Y的分布律如表1所示，试问哪个射手的射击技术较好？

表1　X和Y的分布律

甲乙射击水平的高低完全由其分布律决定，这是毋庸置疑的，但在比较分布律时遇到困难，针对不同环数甲、乙的高低水平不一样.而实践是检验真理的唯一标准，因此让甲、乙各射击n次，其命中情况如表2所示，比较他们射击一次的平均命中环数.

表2　甲、乙射击的命中情况

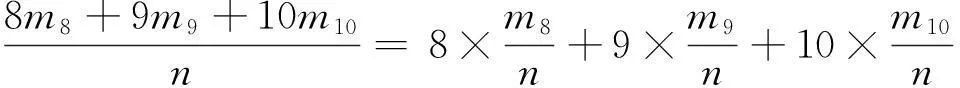
乙射击一次的平均命中环数近似为

对比9.3和9.1两个结果，可以容易地看出甲的射击水平高于乙的射击水平.进一步，总结该引例的求解过程，平均命中环数近似等于命中环数乘以相应概率再进行累加，因此得到离散型随机变量的数学期望的定义.

2数学期望的含义

从定义公式的整理形式还可以看出，随机变量的数学期望本质上就是以概率为权的随机变量取值的平均值，反映了随机变量的“平均方面”的特征，因此，数学期望构成了进行水平判定的重要依据，正如引例中利用数学期望评判射击水平的高低.

3连续型随机变量的数学期望的定义

关于数学期望，现在只有离散型随机变量数学期望的定义，因此，落脚点还应该在离散型随机变量的数学期望上.这里采用数学上的一个典型思路“连续问题的离散化”.我们希望构造一个合适的离散型随机变量去近似一个连续型随机变量[3].问题就是这个离散型随机变量应该如何构造呢？

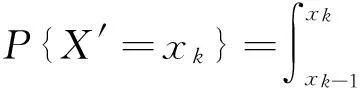
4数学期望的应用

根据数学期望的含义，数学期望反映了随机变量取值的“平均”特征，因此数学期望主要用于判定水平高低(在保险等行业中也可以控制风险大小).数学期望被广泛应用于工业的质量控制、农业的农田试验、医学的疗效检验、国防的效能分析、气象的灾害预报等[4].

美国数学协会组织的美国数学竞赛[5](American Mathematics Competition，AMC)始于1950年，是为所有喜爱数学的学生所开发的，还可以筛选出具有特殊天赋者.AMC试题简难兼具，使任何程度的学生都能感受到挑战.试题由25道选择题构成，每道题有5个选项，只有一个正确答案.它的评分标准是答对一题得6分，答错不扣分，但是未答得1.5分.将评分标准做个整体平移，相当于答对一题得4.5分，答错扣1.5分，未答得0分,而我们一般遇到的评分标准是答对一题得4.5分，答错和未答得0分.下面从数学期望的角度论证评分标准的合理性.

根据考试经验，遇到不会的题目，很多人不会空着，而是随便猜个选项，那么就假设某人凭运气猜题，记X=“在AMC评分标准下，他的题目得分”，Y=“在一般评分标准下，他的题目得分”.显然，X和Y都是随机变量，其中X的取值和对应概率只有两种情况，猜对了得4.5分，猜错了得-1.5分，并且猜对的概率为1/5，猜错的概率为4/5.通过数学期望计算公式可知，他的平均得分为

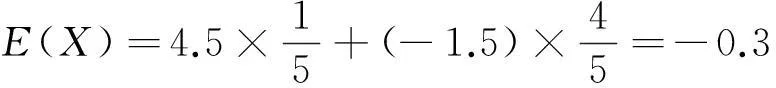
类似地，Y的取值和对应概率也只有两种情况，猜对了得4.5分，猜错了得0分，并且猜对的概率为1/5，猜错的概率为4/5，因此，Y的数学期望为

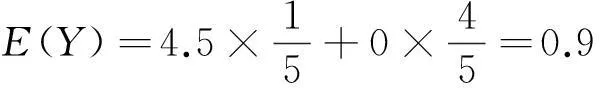
可以看出，在不同的评分标准下，一个胡乱猜答案的人的平均收益是不同的，在AMC评分标准下胡乱猜答案者不但没收益，还有损失，而在一般评分标准下胡乱猜答案者总是有收益的.这说明了在AMC评分标准下鼓励学生按照自己的实际能力进行答题，即所谓“知之为知之，不知为不知”，因此也更能考察出学生的实际水平.通过这个简单题目的求解，让学生更深刻地认识到数学期望的应用场合.

5小结

实践证明，通过把数学期望定义的教学分解为4个问题的解决，不仅能充分调动学生学习的兴趣和主动性，而且有利于培养学生解决问题的能力和知识迁移的能力.

参考文献

[1]盛骤，谢式千，潘承毅．概率论与数理统计[M]．北京：高等教育出版社，2008:90-91.

[2]熊欧，仇海全，武洁. 数学期望的教学方法新探[J]. 科技信息,2010(8):12.

[3]华剑. 连续型随机变量的数学期望定义探析[J].考试周刊,2008(30):44.

[4]苗慧. 论概率中数学期望在实际生活中的应用研究[J].中国科教创新导刊,2013(29):24-27.

[5]百度百科.美国数学竞赛[EB/OL].[2015-09-12]. http://baike.baidu.com/view/6910868.htm.

Discussion on Teaching the Definition of Mathematical Expectation Based on Problem-driven

LI Xinna1, CHEN Ke2

(1.School of Science, Information Engineering University, Zhengzhou 450002, China;2.InstitutionofNavigationandAerospaceEngineering,InformationEngineeringUniversity,

Zhengzhou450002,China)

Abstract:Based on the problems, the teaching procession of the definition of mathematical expectation is divided into four layers： the definition of discrete random variable mathematical expectation, the meaning of mathematical expectation, the definition of continuous random variable mathematical expectation and the application of mathematical expectation.

Key words:mathematical expectation; problem-driven; discrete; continuous

收稿日期：2015-11-28

基金项目：信息工程大学教育教学项目(XD6201513C)

作者简介：李新娜(1982—)，女，河南确山人，信息工程大学理学院讲师，博士，主要研究方向：应用统计．

doi：10.3969/j.issn.1007-0834.2016.02.016

中图分类号：G642.0;O211.67

文献标志码：A

文章编号：1007-0834(2016)02-0067-03