计算机辅助教学对数学创造性思维的影响研究
王华
[摘 要] 计算机辅助教学(CAI)在高中数学课堂中得到了广泛的应用,那么如何让它更有利于发展学生的创造性思维,构建计算机辅助教学特有的教学模式,本文采用等组折中控制前后测实验法对高一学生进行了实验研究,从计算机辅助教学的几个特性分析了实验结果,得到了一些反思.
[关键词] 计算机辅助教学;创造性思维;实验研究
在高中数学新课程标准推广的近几年,计算机辅助教学(CAI)已在各校的高中数学课堂中广泛的应用,它打破了原有的粉笔加黑板的传统数学教学方式,引起了课堂内容的变革. 但计算机辅助教学除了改革高中数学课堂的教学模式,它对高中学生的数学创造性思维是否有影响,是否有利于学生创造性思维的发展以及在教学实验的实践中不断积累计算机辅助教学的教学资料,逐步构建计算机辅助教学的教学模式,为其在校内乃至更大的范围的推广积累经验. 带着这两个目的,笔者对2014届高一新生进行了调查研究.
前期准备
本课题的研究方法为实验法.实验假设为计算机辅助教学有助于高一学生创造性思维的发展. 实验设计采用等组折中控制前后测实验法. 实验对象为14届高一新生,将其随机分派编班后,随机抽出两个班,其一为实验班(高一1班),其二为控制班(高一7班). 实验因子为计算机辅助数学教学. 本实验的测量工具采用自编的数学创造性思维检测题.
本课题研究的理论基础——建构主义学习理论及创造性思维培养理论,结合高中生的学习心理特点,初步构建了计算机辅助数学教学以培养学生创造性思维的教学模式.
操作过程
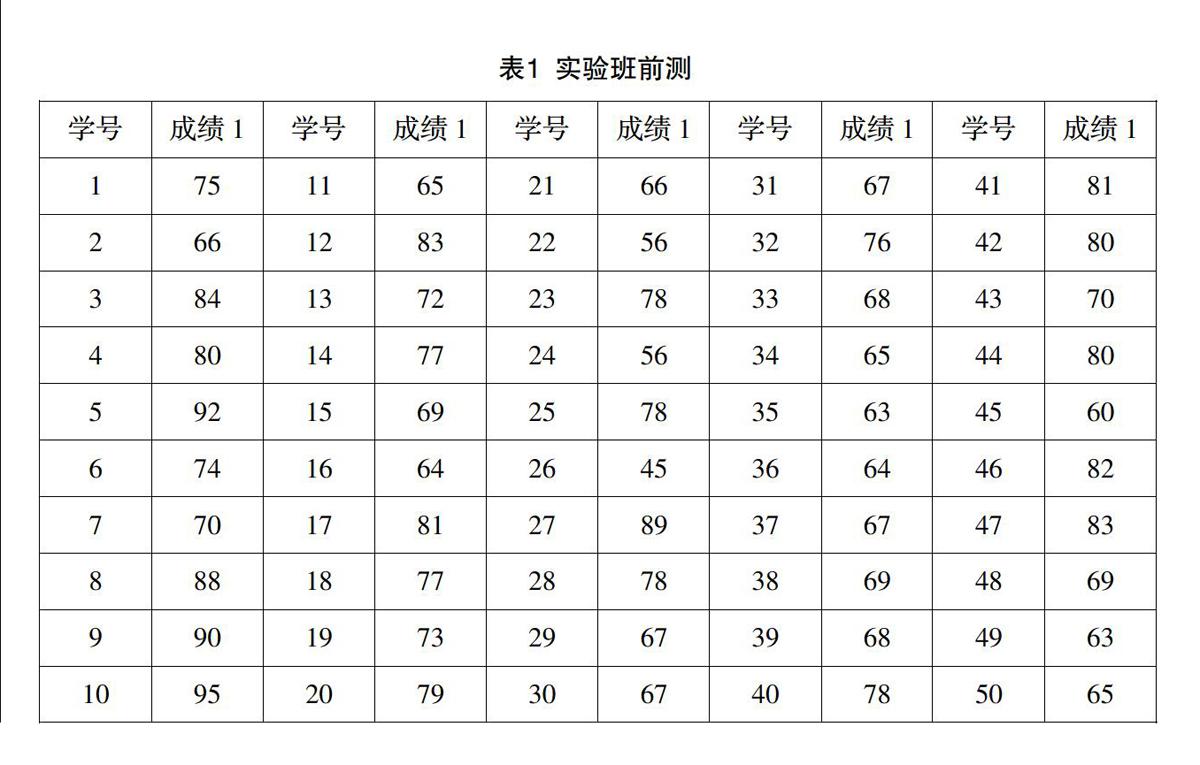
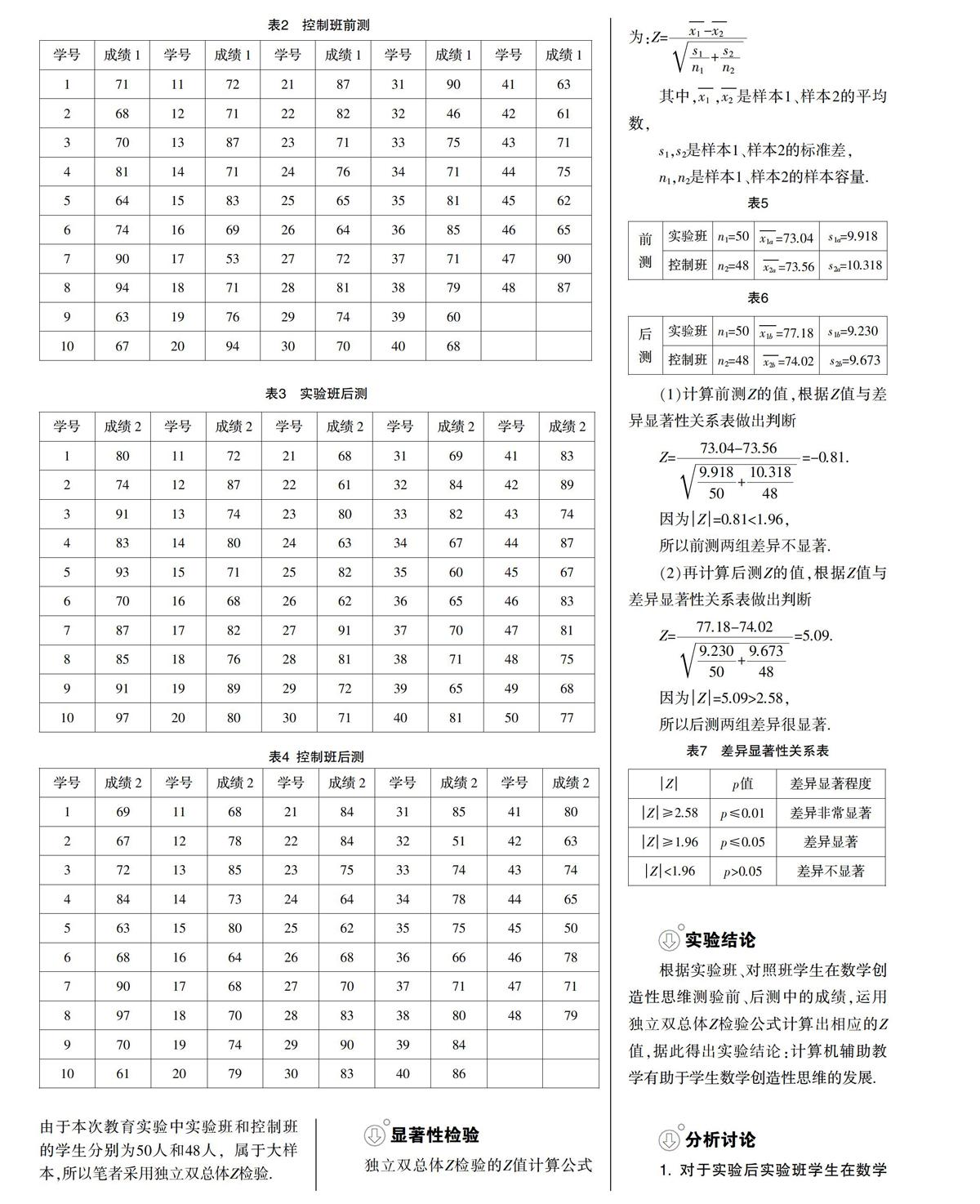
笔者于9月4、5、6三天对实验班及控制班学生分别进行了《数学创造性思维测验》的前测. 其原始数据见表1、2.
之后对实验班学生导入实验因子.本实验中计算机辅助数学教学主要应用的软件是平台型工具软件“几何画板”.
笔者于11月5日对实验班及控制班学生分别施以《数学创造性思维测验》的后测. 其原始数据见表3、4.
最后对两组数据进行显著性检验.由于本次教育实验中实验班和控制班的学生分别为50人和48人,属于大样本,所以笔者采用独立双总体Z检验.
实验结论
根据实验班、对照班学生在数学创造性思维测验前、后测中的成绩,运用独立双总体Z检验公式计算出相应的Z值,据此得出实验结论:计算机辅助教学有助于学生数学创造性思维的发展.
分析讨论
1. 对于实验后实验班学生在数学创造性思维测验中成绩显著提高的原因分析
根据对本教学实验有关数据的分析,在实验后,实验班学生在数学创造性思维测验上成绩显著高于对照班学生,笔者认为导致这一结果的可能原因有以下几点:
(1)计算机辅助教学的直观形象性为学生的形象思维提供了丰富的素材,有助于数学模型在学生头脑中的构建,从而为创造想象和直觉思维的发展提供了条件.
多媒体计算机的高速运算功能和位图模拟功能,能够将复杂的数学变化过程瞬间模拟完成,并将其运动过程及函数图象显示于屏幕之上,使学生能对难以掌握的、多变的运动中间暂态过程及函数曲线一目了然.
计算机辅助教学的直观形象性,不仅有利于学生形象思维的发展,也为学生的逻辑思维提供了鲜活的材料. 学生可以分析,小球之所以这样运动、形成这一轨迹,其原因何在?如果改变其中一种或几种条件,其轨迹又将如何?在学生假想、验证的过程中,其直觉思维、创造想象以及逻辑思维均得到发展. 从某种意义上说,学生利用这一教学软件自主地去研究,对于学生数学直觉思维的发展及探索精神的养成,远比教师讲解更为有效.
(2)学生利用工具型软件解决学科具体问题的过程本身就是一种创造性劳动,其思维结果具有创造性.
《几何画板》属于工具型软件,是高中数学课堂中常用的辅助软件. 例如,作一条已知线段AG的N等分点(N为自然数,比如为6). 传统的作法是过点A作一条射线,在这条射线上用圆规以A为端点以任意长度截取六条等长线段,AB1,B1C1,C1D1,D1E1,E1F1,F1G1. 然后连接GG1. 分别过B1,C1,D1,E1,F1五个点作GG1的平行线,交线段AG于B,C,D,E,F五点. 可以证明这五点将线段AG六等分,B点为线段AG的六等分点. 若想继续作线段AG的五等分点、四等分点、三等分点、二等分点,可依法炮制.
在常规教学中,除这一作法外,尚无其他可行作法.然而在本次教育实验中,有一个小组的学生利用《几何画板》发现了另一种作法:仍然是作已知线段AG的六等分点,在《几何画板》中画线段AG(长6 cm),以A为端点作AG的垂线段AA1,再以AA1和AG为两邻边作一矩形A1AGG1. 连接这一矩形的两条对角线交于点F1,过F1作AG的垂线交AG于点F,利用《几何画板》的度量工具可知,AF为AG的. 连接A1F交AG1于点E1,过E1作AG的垂线交AG于点E,利用《几何画板》的度量工具可知,AE为AG的.连接A1E交AG1于点D1,过D1作AG的垂线交AG于点D,利用《几何画板》的度量工具可知,AD为AG的. 以此类推,可以分别找到点C、点B.
用这种方法可以找到任意已知线段的N等分点,但欲进行几何证明则相当困难,因而在目前的中学教材中尚无这种作法的先例. 而该组学生通过创造想象和直觉思维,利用《几何画板》的度量功能,发现了这一作法. 类似的例子在本次教育实验中并不少见. 由此可见,这类工具型软件为学生们提供了更为广阔的思维空间,使得他们的许多想象乃至一些异想天开的想法能够在一个虚拟的世界里得到验证. 碰壁,会迫使他们去做更加缜密的逻辑思考. 在这种发现问题、提出假设、检验假设、发现新问题、提出新假设、再检验直至解决问题的过程中,学生的创造性思维得到发展.
(3)计算机辅助教学将以往对数学问题的静态研究转变为动态研究,学生更容易掌握问题的本质,有利于学生空间想象能力、逻辑思维能力以及辩证思维能力的发展.
几何学研究的精髓在于对空间内点、线、面关系的研究. 比如,点运动成线,线运动成面,面运动成体. 一条圆弧,绕不同的轴旋转,所成的“体”是千变万化的,凭一块黑板、一支粉笔,教师很难给学生一个形象、具体的答案. 而利用《几何画板》,学生可以随心所欲地设定圆弧的形状,选取旋转轴,观察旋转所成的体.当然,这只是极为简单的例子,对于一些更为复杂的空间点、线、面关系的解析,《几何画板》更能显示其强大的功能. 学生在这个特殊的几何实验室内可以通过拖动点、线,旋转面,去研究它们之间相互关系的本质,这对于学生空间想象能力、逻辑思维能力以及辩证思维能力的培养意义重大.
2. 关于本教育实验的两点思考
(1)对于促进学生创造性思维发展起决定性作用的,并非是以多媒体计算机为代表的现代教育技术本身,而是具有创造性人格特征的教师对这些技术的创造性应用.
(2)技术不是万能的,计算机辅助教学存在局限性. 如前所述,计算机辅助教学具有传统的教学手段无法比拟的优越性,诸如,能够对肉眼观测不到的微观、宏观现象进行形象、逼真的模拟,能够演示理想状态下物体的运动过程及中间暂态,能够将静止、孤立的点、线、面进行动态研究,等等. 然而,虚拟的终归是虚拟的. 技术本身为学生研究、探索提供了条件,他们可以凭借技术在一个虚拟的世界里,使某个问题简单化、绝对化,甚至可能是荒唐的;但他们最终需要从这个虚拟的世界里走出来,去面对复杂的、变化着的真实环境,去解决真实世界里的现实问题.
因此,计算机辅助教学尽管有着传统教学手段无法比拟的优越性,却不可能完全取代传统的教学手段. 二者需要有机结合,才能相得益彰,更好地促进学生的发展.

