5元素集合上T0拓扑总数的计算
荣宇音,徐罗山
(扬州大学数学科学学院,江苏扬州225002)
5元素集合上T0拓扑总数的计算
荣宇音,徐罗山
(扬州大学数学科学学院,江苏扬州225002)
利用有限偏序集上的几个重要结果并借助于拓扑空间对应的特殊化序与拓扑之间的关系计算得出5元素集合上T0拓扑总数为4231,拓扑总数为6942.
有限偏序集;拓扑;极小元;T0拓扑总数
§1 引 言
拓扑学[1]中有一个艰难的问题是给出n元素集合上拓扑总数的计算.为了计算n元集合上的拓扑总数,对于较小的n可以通过手工验证进行计算;对于稍大一点的n则可以通过计算机编程进行穷举计算,但这很难体现数学方法和思维.当然如果不借助于计算机编程,要算出n元素集合上的拓扑总数,则可先考虑计算T0拓扑总数和非T0拓扑总数,其中T0拓扑总数的计算更具方法性和技巧性,而非T0拓扑总数可以通过较小n情形的T0拓扑总数经递推计算得到.于是要计算n元素集合上拓扑总数关键是要计算n元素集合上T0拓扑总数.从Domain理论与拓扑的交叉应用[2-6]入手,文[7]已经算出了对于n=1,2,3和4的T0拓扑总数分别是1,3,19和219,相应的拓扑总数分别是1,4,29和355.随着n的增大,计算这些总数难度会越来越大.本文从序与拓扑的交叉出发,在文[7]的基础上并利用文[7]的理论和方法,结合Hasse图[8],进一步给出了5元素集合上T0拓扑总数和非T0拓扑总数的计算,它们分别是4231和2711,从而得到5元素集合上拓扑总数是4231+2711=6942.本文所用的方法还可望向n的更大情形推广.
§2 若干相关概念和引理
先给出几个相关概念,它们大都采自文献[2]和[8].
设X为集合,则X上的自反且传递的二元关系均称为X上的预序,记为≤.X上的一个预序,如果还是反对称的,即由x≤y≤x可得x=y,则称这样的预序为偏序.设≤为X上一个预序(或偏序),则称(X,≤)为一个预序集(或偏序集).此时也称X为一个预序集(或偏序集).
设(X,≤)为偏序集.对x,y∈X,用x<y表示x≤y且x 6=y.若x<y不成立,则记为x≮y.
设X为预序集,m∈X称为一个极小元,如果X中任一元x,当x≤m时,有m≤x成立.X的非空子集D称为X的定向集,若对任意a,b∈D,存在c∈D使a≤c,b≤c.
设A ⊆ X,记↑A={y∈X :∃x∈A,x≤ y}及↓A={y∈X :∃x∈A,y≤ x}.简记↑{y}为↑y及↓{y}为↓y.
定义2.1[2,6]设X为预序集,A⊆X.A称为X的Scott-闭集,如果满足:(1)A=↓A;(2)对任意定向集D⊆A,若上确界supD存在,则有supD∈A.X上的全体Scott-闭集记为σ∗(X).X上Scott-闭集的补集全体形成X上的拓扑称为Scott拓扑,记作σ(X).
易知偏序集上的Scott拓扑均为T0拓扑.又如X是有限预序集,则σ(X)={↑A|A⊆X}为X的全体上集.
定义2.2[2,6]设X为拓扑空间.X上的特殊化序≤定义为x≤y当且仅当x∈{y}-,其中{y}-为独点集{y}的闭包.
下列命题和引理的是本文的理论基础,证明详见文献[7]中相应结论的证明,这里从略.
命题2.1 预序集X的序和其上Scott拓扑的特殊化序是一致的.又若X为T0拓扑空间,则X上特殊化序为偏序.若X为非T0拓扑空间,则X上特殊化序为预序而非偏序(这样的预序称为真预序).
引理2.1 设X为有限集,τ和η为X上两个拓扑,则τ=η当且仅当它们诱导的特殊化序相同.又设≤1和≤2为X上两个预序,该两预序相同当且仅当它们诱导的Scott拓扑相同.
注2.1 (1)对于无限集,其上两个不同的拓扑可诱导相同的特殊化序,例如有限补拓扑和离散拓扑诱导的特殊化序均为离散偏序.
(2)上一引理是说,有限集上的拓扑与其上的预序形成一一对应且T0拓扑对应于偏序,而非T0拓扑对应于真预序.
引理2.2 (Zorn引理)在任何一个非空的偏序集中,如果任何一个全序子集都有上界,那么这个偏序集必然存在极大元.对偶地,在任何一个非空的偏序集中,如果任何一个全序子集都有下界,那么这个偏序集必然存在极小元.
引理2.3 设X为偏序集,min(X)为X的极小元之集.则当x∈Xmin(X)时,断言存在y0∈X使y0<x.
引理2.4 设X为有限偏序集,min(X)为X的极小元之集.则∀y∈X有↓y∩min(X)6=∅.
定理2.5 设X为有限偏序集,min(X)为X的极小元之集,则当x∈Xmin(X)时,存在m0∈min(X)使m0< x.
§3 5元素集合上非T0拓扑数计算
由引理2.1知,n元素集合上非T0拓扑数对应的是n元素集合上真预序数.对于真预序集,满足条件x≤y≤x的元x和y称为等价元.当然,一个真预序集至少有两个元等价.用Yi和Pi分别表示i个元素集合上真预序数和偏序数.由文[7]知,Y1=0,P1=1,Y2=1,P2=3,Y3=10,P3=19,Y4=136,P4=219.
下面计算Y5而得到5元素集合上非T0拓扑数.我们将按等价元的个数进行分类计算.
情形1:含5个等价元,即5个元均等价,共有一种真预序.
情形2:含4个等价元,此时有4个元相互等价,该4元可看成一个整体,与剩下的一个元形成二元偏序,这种情形共有×P2=×3=15个真预序.
情形3:含3个等价元,这时又有两种情况.一是除3等价元外,剩下的两元不等价,这时将3等价元看成整体与剩下两元形成3元偏序,这种情况共有
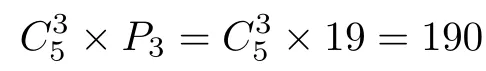
个真预序;二是除3等价元外,剩下的两元也等价,这时将两组等价元看成两个整体形成二元偏序,这种情况共有
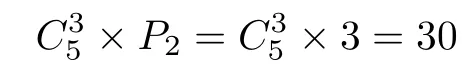
个真预序.故情形3共有190+30=220个真预序.
情形4:含两个等价元,这时又有两种情况.一是除两等价元外,剩下的3元不等价,这时将两等价元看成整体与剩下3元形成4元偏序,这种情况共有
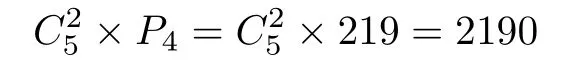
个真预序;二是除两等价元外,剩下的3元中有两元也等价,这时将两组等价元看成两个整体与剩下一元形成3元偏序,注意到对称性,这种情况共有
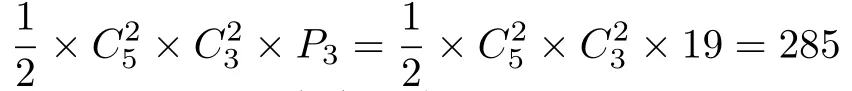
个真预序.故情形4共有2190+285=2475个真预序.
四种情形合计共有真预序数为1+15+220+2475=2711.
综之,5元素集合上共有2711个真预序,即Y5=2711,从而其上共有2711个非T0拓扑.
§4 5元素集合上T0拓扑数计算
由引理2.1,为计算5元素集合上T0拓扑数,只需计算5元素集合上偏序数P5.下面依极小元个数进行分类计算.
情形1:含5个极小元,这时是离散偏序,仅有1个偏序.
情形2:含4个极小元(见图1).这时4个极小元相互不可比较,又由定理2.5,剩下的一个元至
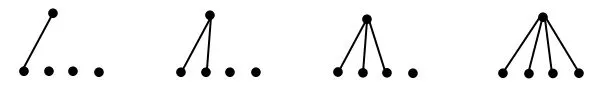
图1 含4个极小元
少大于一个极小元,也可能大于两个或3个或4个极小元,这种情形共有偏序数为
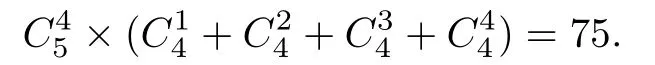
情形3:含3个极小元,此时分两种情况.
(1)剩下两元不可比较(见图2).则每元与3极小元形成偏序数分别为++=7,这
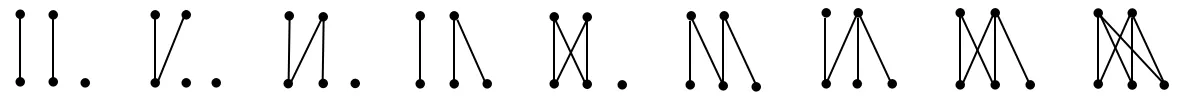
图2 含3个极小元(1)
种情况共有偏序数为
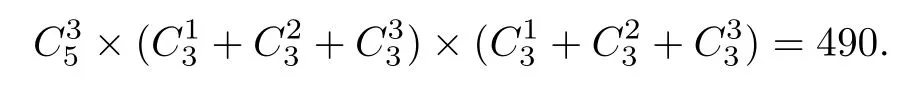
(2)剩下的两元可比较(见图3).由定理2.5,该两元中的较小元至少比一个极小元大,当较小

图3 含3个极小元(2)
元比3极小元中的1个大时,较大的元可比另外二个极小元中0个或1个或2个大,共有×(++)=12种选择;若较小的元比其中两个极小元都大时,这时较大的元可比另外一个极小元中0个或1个大,共有×(+)=6种选择;若较小的元比3个极小元都大时,这时有=1种选择,从而这种情况共有偏序数为
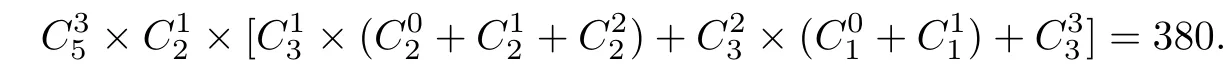
故情形3两种情况合计共有490+380=870种偏序.
情形4:含2个极小元,此时分三种情况.
(1)剩下3元不可比较(见图4).则每元与两极小元形成偏序数分别为+=3,这种情况

图4 含2个极小元(1)
共有偏序数为
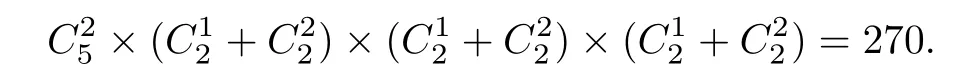
(2)剩下的3元中至少有两元可比较,此时这3元按极大元的情况可以分成两类.
(I)极大元有两个(见图5).此时若(A)两极大元都比剩下的第三元大时有=3种,由定
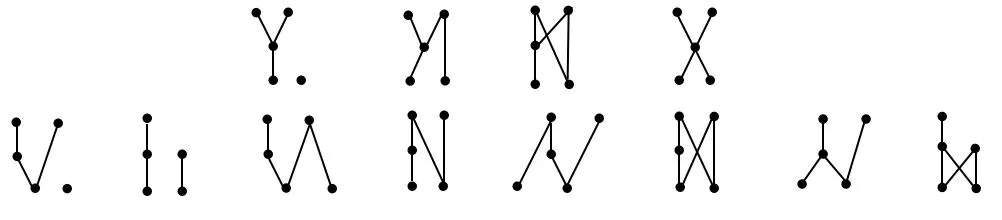
图5 含2个极小元(2)-(I)
理2.5,该第三元至少比一个极小元大,当该第三元比两极小元中的1个大时,两极大元都可比另外一个极小元中0个或1个大,共有×(+×(+)=8种选择;若该第三元比两个极小元都大时有=1种选择.于是,情形4(2)(I)(A)共有偏序数为
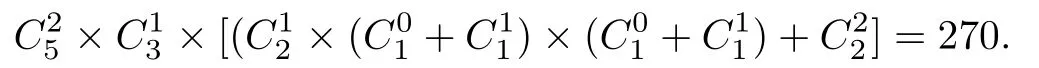
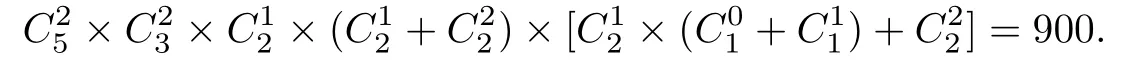
故情形4(2)(I)共有偏序数为270+900=1170.
(II)极大元有一个(见图6).此时剩余两较小元,每个较小元至少比一个极小元大,每个较小

图6 含2个极小元(2)-(II)

综之,情形4(2)共有偏序数为1170+330=1500.
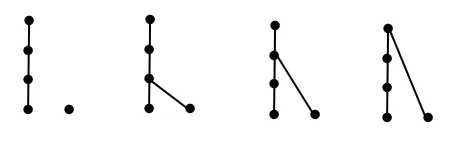
图7 含2个极小元(3)
故情形4(3)共有偏序数为
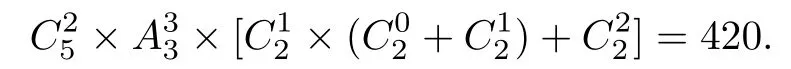
综之,情形4的三种情况合计有270+1500+420=2190个偏序.
情形5:含1个极小元(见图8).这时由定理2.5,该极小元也是最小元,从而剩下的4个元形成4元偏序,这种情形共有偏序数为
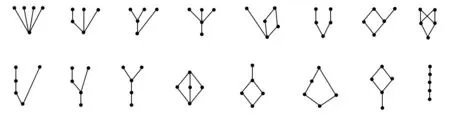
图8 含1个极小元
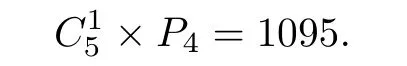
于是,5元素集合上偏序数P5=1+75+870+2190+1095=4231.从而5元素集合上T0拓扑个数为4231.
综之,5元素集合上非T0拓扑数为2711,T0拓扑数为4231,而不同拓扑总数为6942.
§5 结论
本文利用偏序与拓扑之间的关系以及有限预(偏)序集的性质给出了5元素集合上非T0拓扑总数和T0拓扑总数的计算.结果是:5元素集合上非T0拓扑数为2711,T0拓扑数为4231,而不同拓扑总数为6942.
这种计算方法易于被人们理解,并可望向n=6,7甚至更大的n情形推广.
致谢 扬州大学数科院研究生陈振超利用计算机编程验证了本文的上述结果,特此致谢.
[1] Engelking R.General topology[M].Warszawa:Polish Scienti fi c Publishers,1977.
[2] Gierz G,Hofmann,K H,Keimel K,et.al.Continuous Lattices and Domains[M].Cambridge:Cambridge University Press,2003,1-263.
[3] Lawson J D.The duality of continuous posets[J].Houston Journal of Mathematics,1979,5:357-394.
[4] Scott D.Continuous lattices[J].Toposes,algebraic geometry and logic,Lecture Notes in Mathematics,Berlin:Springer,1972,274:97-136.
[5] Xu Luoshan.Continuity of Posets via Scott Topology and Sobri fi cation[J].Topology and Its Applications,2006,153:1886-1894.
[6] 何青玉,徐罗山.Scott闭集格的C-代数性及其应用[J].高校应用数学学报,2014,29(3):369-374.
[7] 荣宇音,徐罗山,谢丽娜.有限偏序集与4元素集合上T0拓扑总数的计算[J].高校应用数学学报,2015,30(4):457-461.
[8] 屈婉玲,耿素云,张立昂.离散数学[M].北京:高等教育出版社,2012,1-150.
Calculating of the total number of T0-topologies on a 5-element set
RONG Yu-yin,XU Luo-shan
(Department of Mathematics,Yangzhou University,Yangzhou 225002,China)
Based on some results for fi nite posets and the specialization order of a topology,as well as relationships between topologies and orderings,we calculate the total number of T0-topologies on a 5-element set,which is 4231.We also calculate the total number of di ff erent topologies on a 5-element set,which is 6942.
fi nite poset;topology;minimal element;the total number of T0-topologies
54C35;06A11
O153.1;O189.1
A
:1000-4424(2016)04-0461-06
2016-01-30
2016-10-08
国家自然科学基金(11671008;61472343);江苏省高校自然科学基金(15KJD110006);江苏高校品牌专业建设工程项目(PPZY2015B109);扬州大学大学生学术科技创新基金

