删失截断情形下失效率变点模型的Bayes参数估计

何朝兵

(安阳师范学院数学与统计学院,河南安阳455000)

删失截断情形下失效率变点模型的Bayes参数估计

何朝兵

(安阳师范学院数学与统计学院,河南安阳455000)

通过添加部分缺失寿命变量数据,得到了删失截断情形下失效率变点模型相对简单的似然函数.讨论了所添加缺失数据变量的概率分布和随机抽样方法.利用Monte Carlo EM算法对未知参数进行了迭代.结合Metropolis-Hastings算法对参数的满条件分布进行了Gibbs抽样,基于Gibbs样本对参数进行估计,详细介绍了MCMC方法的实施步骤.随机模拟试验的结果表明各参数Bayes估计的精度较高.

失效率;指数分布;EM算法;Gibbs抽样;Metropolis-Hastings算法;截断正态分布

§1 引 言

在可靠性统计中,已工作到某时刻尚未失效的产品,在这个时刻后单位时间内失效的概率称为该产品(寿命)在这个时刻的失效率函数,简称失效率.由于失效率函数能在给定的时刻对瞬间的失效风险进行量化,所以失效率函数在可靠性和生存分析的研究中起着重要的作用.有时失效率函数在某个时刻会突然变化,这个时刻称为变点,例如特别的治疗使病人的身体健康状况在这个时刻有显著改善,疲劳导致机器设备的物理条件在这个时刻急剧下降等.对具有变点的失效率函数的估计是一项有趣和富有挑战性的任务.文献[1]最早研究了失效率变点模型,得到了参数的极大似然估计,接着文献[2]研究了失效率变点的近似置信区间,文献[3]研究了自助法的渐近有效性.关于失效率变点模型的更多研究可参看文献[4-10].

上述的文献大多数都是基于完全数据或右删失数据进行统计推断的.进行寿命试验时,会经常出现截断数据,截断又称为左截断.个体由于某种原因中途撤离了试验,或者被收集的个体信息中途失去或统计数据时个体尚未寿终,这就是右删失.如果个体在研究开始之前就已经寿终或个体本身因条件限制根本无法观察,这样所获得的个体数据就是左截断数据.有时截断和删失会出现在同一个试验中,例如,对前期已经确诊为艾滋病的患者进行研究,感兴趣的变量是患者从确诊到死亡的时间,如果个体在研究的最后提前退出研究或仍然存活,这就是右删失,如果个体在研究还未开始之前就已经死亡,结果导致无法观察,这就是左截断.删失截断数据模型现已广泛应用于生物学、医学、人口学、经济学等方面,对此模型的研究可参看文献[11-14],其中文[11]研究了此模型的回归分析和非参数估计,文[12]研究了此模型下对数正态分布的最大然估计.由于失效率变点模型和删失截断数据模型的广泛应用,所以对删失截断情形下失效率变点模型的研究是一个有意义的研究方向,具有重要的理论价值和实用价值.

Bayes计算方法中的数据添加算法[15]是近年发展很快且应用很广的一种算法,它是在观测数据的基础上加上一些“潜在数据”,从而简化计算并完成一系列简单的极大化或随机模拟,该“潜在数据”可以是“缺损数据”或未知参数.EM算法和Markov chain Monte Carlo(MCMC)方法是两种最常用的数据添加算法.EM算法是一种求后验分布的众数(即极大似然估计)迭代方法,它的每一步迭代由E步(求期望)和M步(极大化)组成.MCMC方法主要包括Gibbs抽样和Metropolis-Hastings算法,通常是Gibbs抽样和Metropolis-Hastings算法相结合得到Gibbs样本,然后基于此样本对后验分布的各种统计量进行估计.EM算法和MCMC方法使贝叶斯统计中许多看起来困难的计算变得简单直观,其应用很广泛,比如约束参数模型,变点模型,截尾数据和分组数据,多个分布的混合等.随着统计计算技术的发展,Bayes计算方法越来越多地应用到变点分析之中.文献[16-18]利用EM算法对变点模型进行了统计推断,文献[19-22]利用MCMC方法研究了变点模型.

由于删失截断数据下的失效率变点模型是截尾数据模型和变点模型的混合,所以贝叶斯计算方法中的EM算法和MCMC方法很适合研究此变点模型.关于截断或删失数据下变点问题的研究已有一些成果,可参看文献[23-26],其中文[23]和[24]分别研究了删失数据下失效率变点问题的非参数和参数估计.对删失并且截断数据下失效率变点模型的研究文只有文[27],但它利用的方法还是传统的最大似然法,它主要依靠一般的数值计算方法分区间逐段寻找变点参数的最大值点,进而得到参数的最大似然估计.而利用EM算法和MCMC方法对删失截断情形下失效率变点模型的研究还未见到.

下文主要利用EM算法和MCMC方法研究了删失截断情形下失效率变点模型的参数估计问题.EM算法中的E步是通过Monte Carlo方法完成的.结合Metropolis-Hastings算法对各未知参数的满条件分布进行了Gibbs抽样,基于Gibbs样本对参数进行估计.随机模拟试验的结果表明各参数Bayes估计的精度较高.

§2 删失截断数据试验模型

设(X,Y,T)是一连续型随机变量,寿命变量X的分布函数为F(x|θ)=P(X ≤x),密度函数为f(x|θ),这里θ是未知参数向量;Y是一右删失随机变量,分布函数为G(y),密度函数为g(y);T是一左截断随机变量,分布函数为H(t),密度函数为h(t),且Y,T的分布与参数θ无关.假定X,Y,T是相互独立非负随机变量.对于n个受试样品(产品寿命),删失截断数据试验模型是,仅在Zi≥Ti时得到观察数据,而在Zi＜Ti下无法得到任何观察值,其中

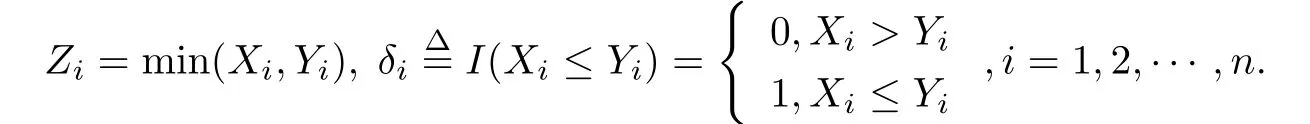
当有样本观察值时,下面求(Zi,Ti,δi)的密度函数.

当Zi=zi,Ti=ti,δi=1时,(Zi,Ti,δi)的密度函数为f(zi|θ)(zi)h(ti),zi≥ti;

当Zi=zi,Ti=ti,δi=0时,(Zi,Ti,δi)的密度函数为g(zi)(zi|θ)h(ti),zi≥ti.

P(无样本观察值)=P(Zi＜Ti)=1-P(Xi≥Ti,Yi≥Ti)

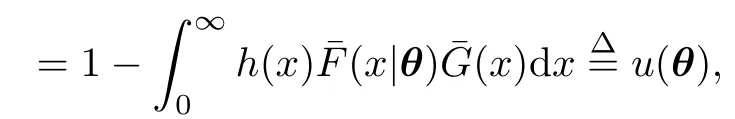
为了研究方便,引入示性变量νi=I(min(Xi,Yi)≥Ti),i=1,2,···,n.

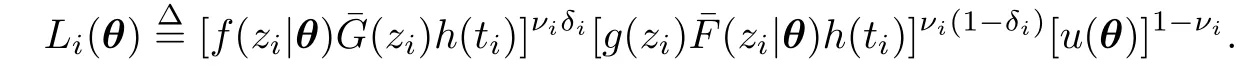
则基于观察数据{(zi,ti,δi)：νi=1,1≤i≤n}的似然函数为

缺损数据下的似然函数比较复杂,参数估计一般很难处理.而Bayes统计中的MCMC算法处理缺损数据非常方便,其方法步骤如下.先引进添加数据,求出添加数据的概率分布,把添加数据作为未知参数处理,然后考虑添加数据和未知参数的后验分布,未知参数的满条件分布可转化为较简单的后验分布,而添加数据的满条件分布则是由添加数据的概率分布抽样,最后分别对各满条件分布进行Gibbs抽样即可.

下面添加缺损的部分Xi的值,以获得较简单的似然函数.

当νi=0时,添加数据Xi=Z1i=z1i.

在min(Xi,Yi)＜Ti的条件下,Z1i的条件密度函数为

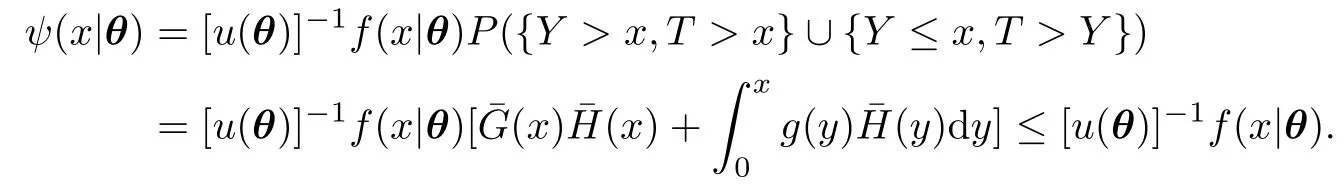
下面利用两种方法随机产生z1i.第一种方法称为舍选法,步骤如下：

若B(x)计算烦琐并且容易产生来自g(y),h(t)的随机数,可以利用第二种方法产生z1i：

(1)分别产生来自f(x|θ),g(y),h(t)的随机数x,y,t;

(2)如果min(x,y)＜t,令z1i=x,停止;

(3)如果min(x,y)≥t,回到步骤(1).

则添加数据后的似然函数为

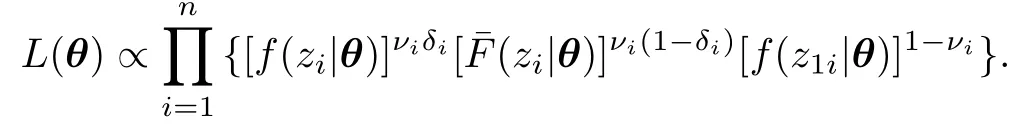
§3 失效率变点模型

设非负连续型随机变量X的分布函数和密度函数分别为F(x|θ)和f(x|θ),称λ(x|θ)=f(x|θ)/[1-F(x|θ)]为X的失效率函数. 若λ(x)满足

(1)对于λi取共轭先验分布Gamma分布Ga(bi,ci),bi,ci已知,即

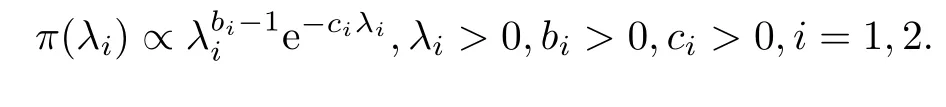
(2)对于τ取无信息先验分布：π(τ)∝1,τ＞0.

假设λ1,λ2,τ相互独立,则

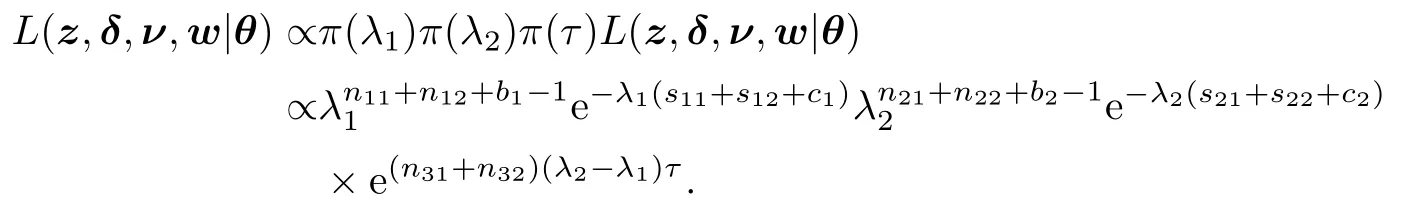
下面讨论截断变量和删失变量都服从指数分布这种特殊情况.

假设Y ∼ Exp(λy),T ∼ Exp(λt),则

下面验证ϕ(x|θ)作为密度函数的规范性.

则Z1i的分布是2个失效率变点模型寿命分布的混合,这个发现很有趣.根据(2)式,还可以利用合成法结合逆变换法直接产生z1i,步骤如下：

(1)产生U(0,1)随机数u1,u2,u3.

(2)计算

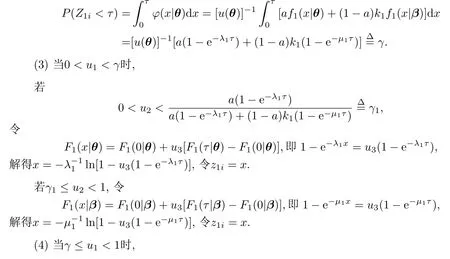
§4 EM算法

EM算法非常适合处理不完全数据,下面利用EM算法来求参数后验分布的众数.假设在第m+1次迭代开始时有估计值则可通过E步和M步得到的一个新的估计.令W表示Z1i组成的向量,为了书写方便,简记(|θ(m),z,δ,ν)为(|·).E步：

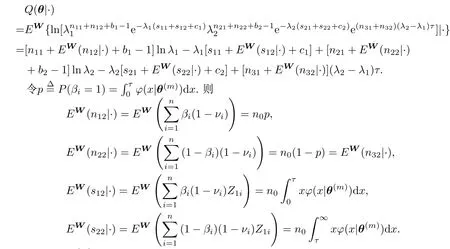
由于ϕ(x|θ(m))为分段函数,积分比较繁琐,大部分情况下要获得期望的显式表示是不可能的,这时可用Monte Carlo方法完成,这就是所谓的Monte Carlo EM(MCEM)方法.

在βi=1的条件下,Z1i的条件密度函数为

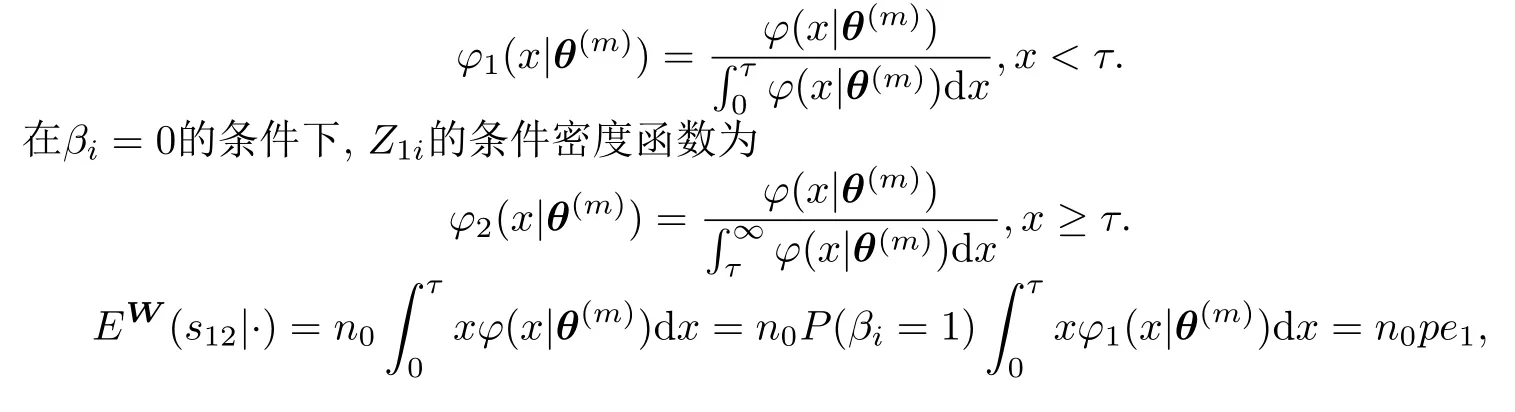
§5 MCMC方法

下面对各参数进行利用Gibbs抽样.首先研究各参数的满条件分布.

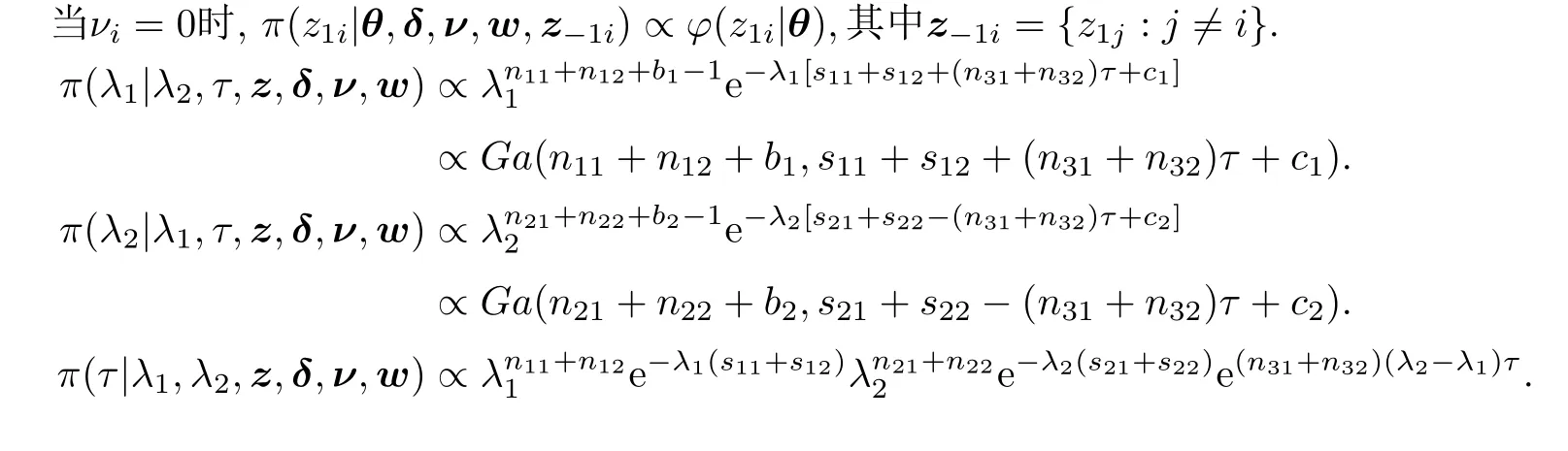
利用前面介绍的舍选法等方法产生z1i,由于λ1,λ2的满条件分布是Gamma分布,所以z1i,λ1,λ2都可以直接Gibbs抽样;但τ的满条件分布比较复杂,不能直接进行Gibbs抽样,利用Metropolis-Hastings算法进行抽样,选取区间(0,+∞)上的截断正态分布作为建议分布.

下面介绍一下截断分布的抽样.

设X是连续型随机变量,其密度函数及分布函数分别是f(x),F(x),x∈(-∞,+∞).令

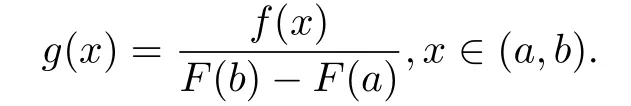
则g(x)是由f(x)定义的在(a,b)上的截断的分布.设F-1(x)为F(x)的反函数,U为由U(0,1)产生的随机数,则F-1{F(a)+U[F(b)-F(a)]}为从g(x)抽取的样本值.

如果X ∼ N(µ,σ2),有F(0)=P(X ≤ 0)= Φ(-µ/σ)=1- Φ(µ/σ),其中Φ为N(0,1)的分布函数.则(0,∞)上截断正态分布的密度函数为

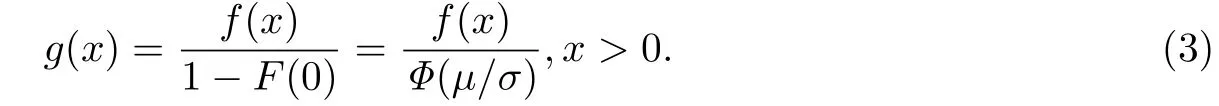
下面介绍MCMC方法的具体步骤.

§6 参数的最大似然估计

为了把参数的Bayes估计与最大似然估计(MLE)进行比较,下面简单介绍MLE的求解步骤.

先考虑左截断右删失模型.为了书写方便,不妨假定后n0个寿命变量没有观察值,前n1=n-n0个寿命变量有观察值z1＜z2＜···＜zn1,则似然函数为

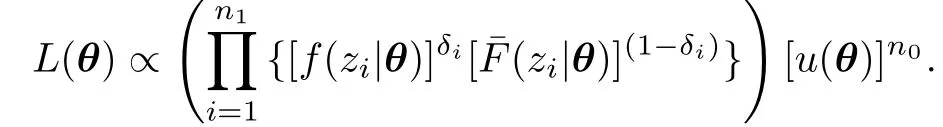
再考虑失效率变点模型,假设τ∈(zk,zk+1],k=0,1,···,n1,其中z0=0,zn1+1=+∞,

§7 随机模拟

下面利用R软件进行随机模拟试验.

随机模拟时取受试样品的个数n=200,θ =(λ1,λ2,τ)=(2,5,0.3),取λ1,λ2的先验分布分别为Ga(0.4,0.15),Ga(2.7,0.5),右删失变量Yi∼Exp(1.5),左截断变量Ti∼Exp(5.5).实际随机模拟数据中,没有观察值的样本个数n0=82,有观察值的样本个数n1=118.各参数的Bayes估计和MLE见表1.

对参数进行EM迭代时选取的初始值为(λ1,λ2,τ)=(5,3,0.8),参数的EM迭代过程见图1至图3.由于在E步是采用的Monte Carlo方法,所以当迭代值围绕一个定值小幅波动时,则可以认为算法收敛了,此时为了增加估计精度,可增加Monte Carlo抽样的数目,再运行迭代一段时间即可停止,停止后,我们把后10次迭代值的均值作为参数的估计值.

对参数进行Gibbs迭代时选取的初始值为(λ1,λ2,τ)=(8,4,2),取B=10000,M=20000,参数的Gibbs迭代过程见图4至图6.对MCMC的收敛性诊断很重要,模拟时可以对参数进行多层链式迭代分析,即输入多组初始值,形成多层迭代链,当抽样收敛时,迭代图形重合.在模拟过程中,输入两组初始值分别进行10000次迭代.各参数的两条迭代链轨迹见图7至图9.另外,为了和EM估计(后验众数估计)相比较,给出基于后M-B=10000个Gibbs样本的核密度众数估计,各参数的核密度估计见图10至图12.

求解参数的MLE时,对τ所在的n1+1=119个区间分别建立对数似然方程组,得到119个解及其对应的对数似然函数值,最大的对数似然函数值对应的解即为要求的MLE.这119个解的τ分量及其对应的对数似然函数值的对照图见图13.

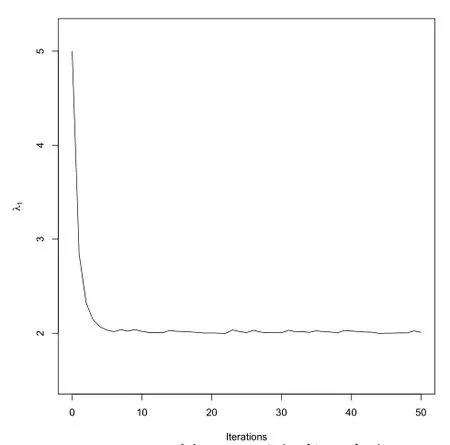
图1 λ1的EM迭代过程

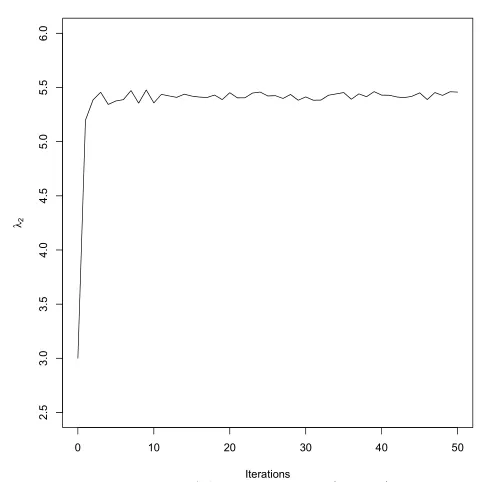
图2 λ2的EM迭代过程

图3 τ的EM迭代过程

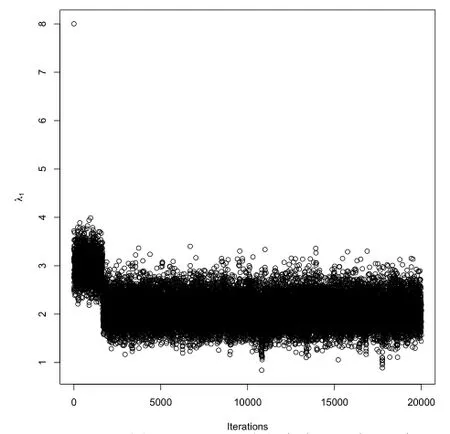
图4 λ1的Gibbs抽样迭代过程

下面进行统计分析：

1)由表1可看出,后验分布的众数估计(即EM估计)、均值估计、中位数估计、核密度众数估计以及MLE的差别很小,λ1,τ估计值与真值的的误差较小,相对误差小于4%;λ2的误差稍大,但相对误差也没超过11%,所以整体上,各参数估计的精度较高.EM估计与后验均值估计、MLE相比误差较小.Gibbs抽样的MC误差也较小,估计效果较好.各参数可信水平为0.95的可信区间可近似取为[2.5%分位数,97.5%分位数],可以看出近似可信区间的长度非常短,所以区间估计的效果也较好.

2)由图1至图3可看出,EM迭代10次左右就收敛了,但由于是利用搜索的方法寻找τ的极大值点,计算机的迭代速度实际上并不快.

3)由图4至图6可看出,Gibbs抽样迭代值波动较小,估计效果较好,虽然Gibbs抽样迭代了20000次,也比EM迭代50次要快得多,这是因为Gibbs抽样迭代完全是利用随机抽样的方法,不必搜索最优值,所以从实际操作角度来说,本文介绍的Gibbs抽样要比EM算法要好.

4)由图7至图9可以发现,各参数的两条迭代链都趋于重合,收敛性较好.

5)由图10至图12可看出,参数核密度的最大值点与对应参数的真值很接近,核密度众数作为后验众数的估计效果较好.

6)由图13可看出,对数似然函数最大值点与参数τ的真值很接近,MLE的精度较高,但对数似然函数方程组比较复杂,所以分区间求解对数似然函数最大值点时非常繁琐,这也是最大似然法的最大缺点.

§8 结 论

图5 λ2的Gibbs抽样迭代过程

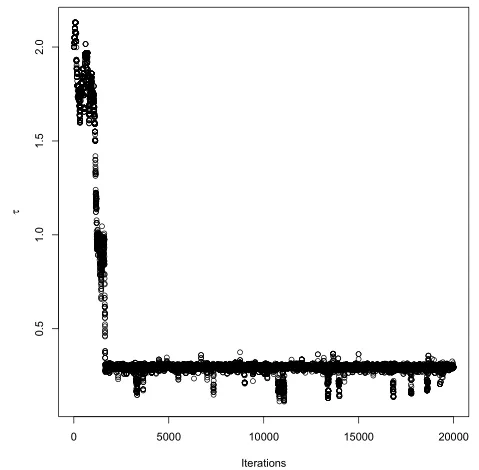
图6 τ的Gibbs抽样迭代过程

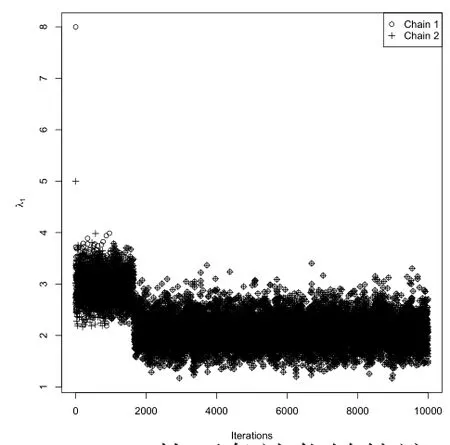
图7 λ1的两条迭代链轨迹

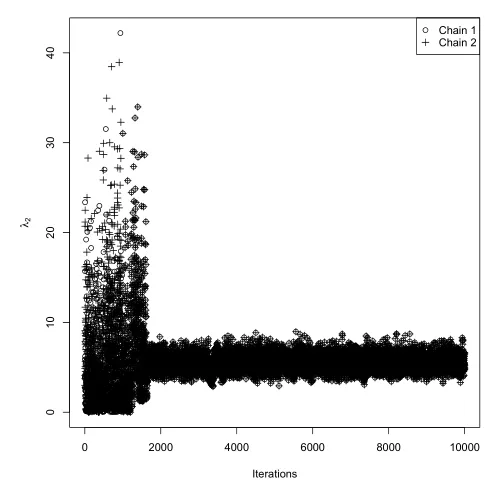
图8 λ2的两条迭代链轨迹

图9 τ的两条迭代链轨迹

图10 λ1的后验核密度估计

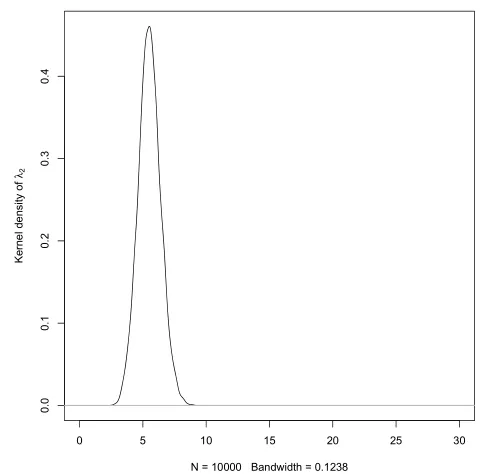
图11 λ2的后验核密度估计

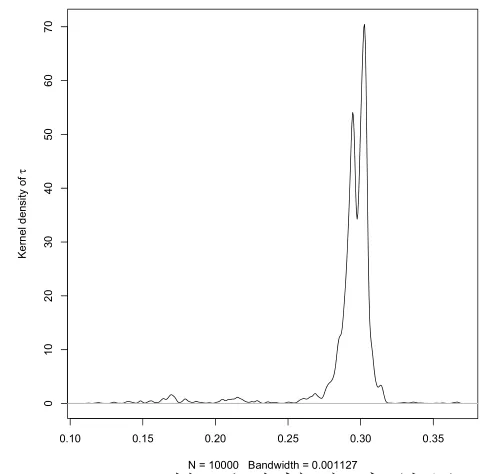
图12 τ的后验核密度估计

本文主要利用Bayes方法研究了删失截断情形下失效率变点模型的参数估计问题.添加了部分缺失寿命变量数据并且讨论了它的概率分布和随机抽样方法.利用EM算法和MCMC方法得到了变点位置参数和其它参数的Bayes估计,随机模拟数据表明参数估计的精度较高.

本文研究的模型是截尾数据模型和变点模型的混合,而EM算法和MCMC方法非常适合处理截尾数据和变点问题,这也是本文的优点.但本文利用的MCEM算法也有缺点,就是利用优化函数对τ进行极大值搜索时速度较慢;虽然本文运用的MCMC的收敛速度比MCEM算法快,但整体上还是慢的,有时MCMC是不收敛的,但还没有有效的改进方法.本文研究变点模型时,假定有1个变点.而如何确定变点的个数,是尚待解决的问题.实际上,变点个数的确定是变点问题中的难题,也是变点研究的发展趋势,更有研究价值和现实意义.

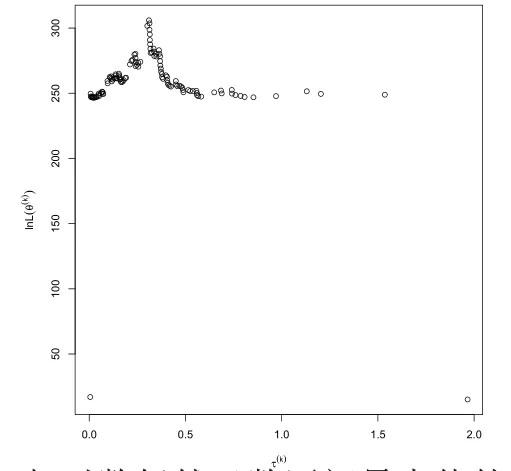
图13 τ与对数似然函数区间最大值的对照图

表1 参数λ1,λ2,τ的Bayes估计和MLE

[1] Matthews D E,Farewell V T.On testing for a constant hazard against a change-point alternative[J].Biometrics,1982,38(2)：463-468.

[2] Loader C R.Inference for a hazard rate change point[J].Biometrika,1991,78(4)：749-757.

[3] Pham T D,Nguyen H T.Bootstrapping the change-point of a hazard rate[J].Annals of the Institute of Statistical Mathematics,1993,45(2)：331-340.

[4] Antoniadis A,Gijbels I,Macgibbon B.Non-parametric estimation for the location of a change-point in an otherwise smooth hazard function under random censoring[J].Scandinavian Journal of Statistics,2000,27(3)：501-519.

[5] Dupuy J F.Detecting change in a hazard regression model with right-censoring[J].Journal of Statistical Planning and Inference,2009,139(5)：1578-1586.

[6] Frobish D,Ebrahimi N.Parametric estimation of change-points for actual event data in recurrent events models[J].Computational Statistics&Data Analysis,2009,53(3)：671-682.

[7]Gijbels I,GürlerÜ.Estimation of a change point in a hazard function based on censored data[J].Lifetime Data Analysis,2003,9(4)：395-411.

[8] Karasoy D S,Kadilar C.A new Bayes estimate of the change point in the hazard function[J].Computational statistics&data analysis,2007,51(6)：2993-3001.

[9] Liu Mengling,Lu Wenbin,Shao Yongzhao.A Monte Carlo approach for change-point detection in the Cox proportional hazards model[J].Statistics in Medicine,2008,27(19)：3894-3909.

[10]Luo Xiaolong,Turnbull B W,Clark L C.Likelihood ratio tests for a changepoint with survival data[J].Biometrika,1997,84(3)：555-565.

[11]Gross S T,Lai T L.Nonparametric estimation and regression analysis with left-truncated and right-censored data[J].Journal of the American Statistical Association,1996,91(435)：1166-1180.

[12]Balakrishnan N,Mitra D.Likelihood inference for lognormal data with left truncation and right censoring with an illustration[J].Journal of Statistical Planning and Inference,2011,141(11)：3536-3553.

[13]Cosslett S R.Efficient semiparametric estimation of censored and truncated regressions via a smoothed self-consistency equation[J].Econometrica,2004,72(4)：1277-1293.

[14]Molanes-lopez E M,Cao R,Keilegom I VAN.Smoothed empirical likelihood con fi dence intervals for the relative distribution with left-truncated and right-censored data[J].Canadian Journal of Statistics,2010,38(3)：453-473.

[15] 茆诗松,王静龙,濮晓龙.高等数理统计(第二版)[M].北京：高等教育出版社,2006.

[16]Yildirim S,Singh S S,Doucet A.An online expectation-maximization algorithm for changepoint models[J].Journal of Computational and Graphical Statistics,2013,22(4)：906-926.

[17]Comert G,Bezuglov A.An online change-point-based model for traffic parameter prediction[J].IEEE Transactions on Intelligent Transportation Systems,2013,14(3)：1360-1369.

[18]Bansal N K,Du H,Hamedani G G.An application of EM algorithm to a change-point problem[J].Communications in Statistics-Theory and Methods,2008,37(13)：2010-2021.

[19]Lavielle M,Lebarbier E.An application of MCMC methods for the multiple change-points problem[J].Signal Processing,2001,81(1)：39-53.

[20]Kim J,Cheon S.Bayesian multiple change-point estimation with annealing stochastic approximation Monte Carlo[J].Computational Statistics,2010,25(2)：215-239.

[21]Yuan Tao,Kuo Yue.Bayesian analysis of hazard rate,change point,and cost-optimal burnin time for electronic devices[J].IEEE Transactions on Reliability 2010,59(1)：132-138.

[22]Liang Faming,Wong W H.Real-parameter evolutionary Monte Carlo with applications to Bayesian mixture models[J].Journal of the American Statistical Association,2001,96(454)：653-666.

[23]Antoniadis A,Grégoire G.Nonparametric estimation in change point hazard rate models for censored data：A counting process approach[J].Journal of Nonparametric Statistics,1993,3(2)：135-154.

[24]Gijbels I,GürlerÜ.Estimation of a change point in a hazard function based on censored data[J].Lifetime Data Analysis,2003,9(4)：395-411.

[25]Huškov´a M,Neuhaus G.Change point analysis for censored data[J].Journal of Statistical Planning and Inference,2004,126(1)：207-223.

[26]Lim H,Sun Jianguo,Matthews D E.Maximum likelihood estimation of a survival function with a change point for truncated and interval-censored data[J].Statistics in Medicine,2002,21(5)：743-752.

[27]GürlerÜ,Yenigün C D.Full and conditional likelihood approaches for hazard change-point estimation with truncated and censored data[J].Computational Statistics&Data Analysis,2011,55(10)：2856-2870.

Bayesian parameter estimation of failure rate model with a change point for truncated and censored data

HE Chao-bing
(School of Mathematics and Statistics,Anyang Normal University,Anyang 455000,China)

By fi lling in some missing data of the life variable,the relatively simple likelihood function of failure rate model with a change point for truncated and censored data is obtained.The probability distribution and random sampling method of the missing data variable fi llled in are discussed.All the unknown parameters are iterated by MCEM algorithm.The parameters are sampled from their full conditional distributions by Gibbs sampler together with Metropolis-Hastings algorithm,and are estimated based on Gibbs sample.The implementation steps of MCMC method are introduced in detail.The random simulation test results show that Bayesian estimations of the parameters are fairly accurate.

failure rate;exponential distribution;EM algorithm;Gibbs sampling;Metropolis-Hastings algorithm;truncated normal distribution

62F15;62N01

O213.2;O212.8

A

：1000-4424(2016)04-0413-15

2016-01-19

2016-07-03

河南省科技攻关计划(162102310384);河南省高等学校重点科研项目(16A110001)