具有HollingⅡ型功能反应和Allee效应的捕食系统模型

蒋 芮, 刘 华,∗, 谢 梅, 魏玉梅, 赵仕凤

(1.西北民族大学数学与计算机科学学院,甘肃兰州730030;2.西北民族大学实验中心,甘肃兰州730030)

具有HollingⅡ型功能反应和Allee效应的捕食系统模型

蒋 芮1, 刘 华1,∗, 谢 梅1, 魏玉梅2, 赵仕凤1

(1.西北民族大学数学与计算机科学学院,甘肃兰州730030;2.西北民族大学实验中心,甘肃兰州730030)

利用计算机模拟方法研究一类离散种群相互作用模型的动态复杂性.通过理论推导建立食饵具有Allee效应和HollingⅡ型功能反应的自治捕食系统模型,用Matlab软件模拟离散种群的生长状态,探索研究参数的变化对种群大小的影响,阐释Allee效应及HollingⅡ型功能反应在种群间相互作用模型中的重要性.研究结果表明：1)当处理时间处于有效区间内时,处理时间越大种群的稳定共存参数域越大;2)Allee效应的引入使种群的动态行为更为复杂,从而增加了捕食者种群的灭绝风险;3)系统受强Allee效应的影响,种群会出现提前分叉现象,如果继续增加Allee效应就会导致种群灭绝;4)强Allee效应更容易使种群趋向灭绝.所得结论在丰富生态学理论的同时,提出了保护生态学的重要依据.

Allee效应;HollingⅡ型;混沌;计算机模拟

§1 引 言

1931年Allee在研究过程中发现群聚的生活状态有利于种群的增长,但是密度太大又会抑制种群的生长甚至会因为资源争夺而走向灭绝.对于每一个种群来说,必定存在着它独立的最适合自身生长繁殖的最佳密度,这就是Allee效应[1-2].Allee效应一直是生态学者研究的重要现象,它描述的是种群的功能效应因种群密度低于某一阈值而出现紊乱所导致的交配功率下降,社会性功能异常或者近交衰退等使种群出现负增长的状态[3-7],严重情况可能导致种群灭绝.生态学家对该效应进行了广泛研究,讨论提出了种群密度与个体生殖和幸存者的正相关关系.2011年Wan-xiong Wang等人对离散的捕食-食饵系统就Allee效应进行了研究,结果表明Allee效应会影响系统的稳定性[8].__________

G.W.Harriso在1979年研究一类具有HollingⅡ型功能反应的捕食者系统模型,利用稳定性的理论得到其奇点的存在性与稳定性[9-10].张娟,马知恩在1996年研究一类具有HollingⅡ型功能反应和两种群均有密度制约的捕食系统模型,得到一个存在唯一稳定极限环的充分条件.1997年朴仲铉和薛春艳在食饵种群具有收获率的模型中,讨论了HollingⅡ型功能反应下的系统生长状态.2003年生物学家Turchin P根据实际情况建立并研究该模型平衡点的存在性,稳定性和极限环不存在性等,作为理论研究的补充.对于HollingⅡ型功能反应的研究主要用于讨论的模型形式[11]如下：

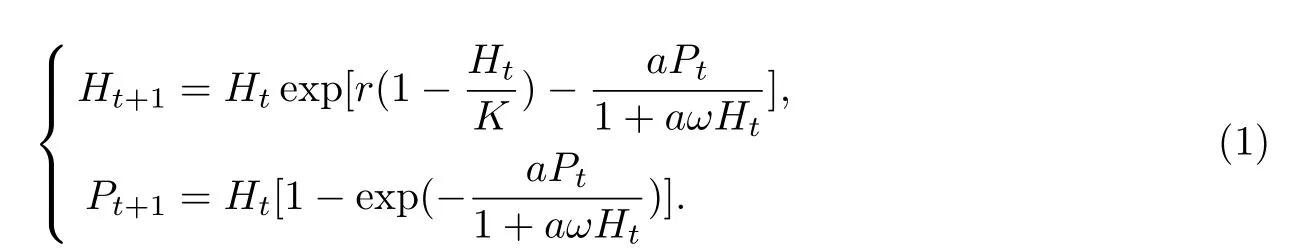
本文以此为基础,为了更进一步的讨论一类离散种群的相互作用系统的动态行为,建立具有Allee效应和HollingⅡ型功能反应的自治捕食系统模型[11-13]：

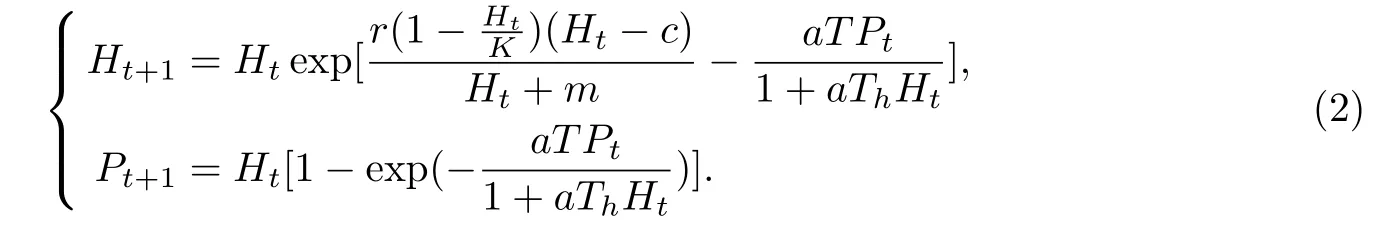
§2 稳定性分析

分析具有Allee效应和HollingⅡ型功能反应的捕食系统的非负平衡点的局部稳定性.

系统(2)具有两个非负的平衡点：平衡点E0=(0,0)对应两种群全部灭绝,正平衡点E∗=(H∗,P∗)对应两种群共存.

定理 对于系统(2)的两个非负平衡点,其局部稳定性具有以下结论：

(1)当c＞0时,平衡点E0=(0,0)是稳定的;

(2)当满足条件-1-C＜B＜1+C且C＜1时,平衡点

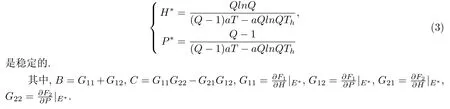
证 为讨论平衡点的稳定性,将模型写成如下形式：

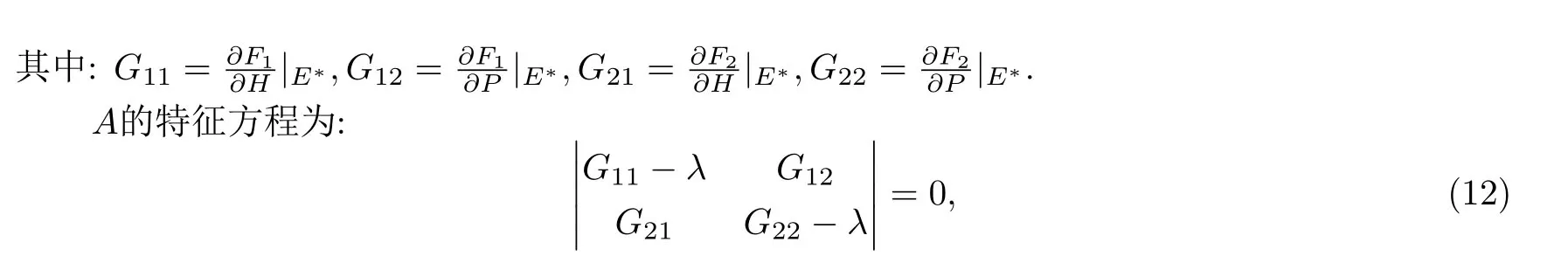
也就是：Q(λ)=λ2-Bλ+C=0.其中：B=G11+G12,C=G11G22-G21G12.

Q(λ)是一条抛物线,当满足如下条件时,方程的根|λ|＜ 1,则平衡点稳定：Q(-1)＞0且Q(+1)＜0且C＜1.解得正平衡点E∗=(H∗,P∗)稳定的条件是

§3 参数对模型动态行为的影响

3.1 处理时间对模型的影响

在食饵-捕食者系统中,捕食者处理食饵的处理时间Th的取值不同,将会直接影响到食饵种群的数量,继而影响捕食者搜寻效率的变化.故在实际的生态环境中需要就捕食者对食饵的处理时间进行讨论分析,该参数取值要符合生态学背景具有一定的取值范围.在对生态系统进行计算机模拟时发现当有效搜寻总时间T=1时,处理时间Th取值在(0.3,0.8)区间内时模拟的生态系统更符合实际情况.故在后面对捕食系统进行模拟时,将捕食者对食饵的捕食过程进行分类讨论,其分岔图如图1所示：图1以搜寻效率a为分岔图横坐标,捕食者种群数量大小P为纵坐标,其余参数取值为：K=5,T=1,c=0.1,m=0.0002,系统初值为H0=5,P0=2.5.由于捕食者的处理时间给定有效区间,所以在计算机模拟的过程中主要选取了三种具有代表意义的处理时间Th的取值进行分析.图1的(a)中为Th=0.3时,即处理时间占比较少的一段时间,动态性非常复杂,在参数a取值为(0.502,1.352)内种群出现稳定共存的生存状态,接着出现混沌状态,在1.37到1.385出现一个比较窄的周期窗,短暂周期后种群再次进入混沌状态,中间有周期窗出现,直到a=1.9648时种群突然灭绝.图1(b)当Th即处理时间占搜寻总时间的二分之一时,该点为讨论处理时间的种群状态的分界点.通过分岔图观察可以发现,与(a)比较当Th增大了两种群稳定共存的参数域扩大了,稳定共存的区间变为了(0.811,5.523),种群依然会出现混沌状态,不过种群灭绝的参数域也扩大了,即在a=5.9492时种群突然灭绝.在图1(c)Th=0.8即处理食饵的时间比较长时,种群出现混沌状态后,该处的混沌状态比较复杂,接着经历倒转的倍周期32周期、12周期、8周期、4周期、2周期,最后经历了一段很长的参数域区间的稳定共存.上述不同的处理时间取值表明当捕食者对食饵进行处理的时间增加会扩大两种群稳定共存的参数域.

3.2 Allee效应常数对模型的影响

通过在捕食者搜寻过程中对食饵的处理时间的分析,我们选择一个相对合适的处理时间参数进行模拟,讨论Allee效应常数在具有Allee效应及HollingⅡ型功能反应模型的动态行为的影响.

图2为具有Allee效应和HollingⅡ型功能反应模型系统的分岔图.以捕食者的搜寻效率a为分岔图参数,即分岔图的横坐标,其余参数取值为：K=5,r=3,T=1,Th=0.4,系统初值为H0=5,P0=2.5.图2(a)为捕食者对食饵不存在Allee效应时的动态系统：当搜寻效率a∈(0.619,2.172)时,两种群出现稳定共存,紧接着显示混沌状态,混沌状态呈现比较复杂的动态行为,比如草叉分支、切叉分支、吸引子危机,有稳定的6周期变化并有明显的周期窗,直到参数变为3.005时种群灭绝.图2(b)为捕食者对食饵具有Allee效应时的动态系统,即参数c=0.1,m=0.5时,从分岔图中可以发现,参数a∈(0.342,0.506)时种群就开始出现混沌状态,在较短的参数变化内出现倒转倍周期分岔,而稳定共存的参数域变为了a∈(0.506,1.705),经历稳定共存后再次出现混沌状态并伴随着周期变化,直到1.985时种群突然灭绝.

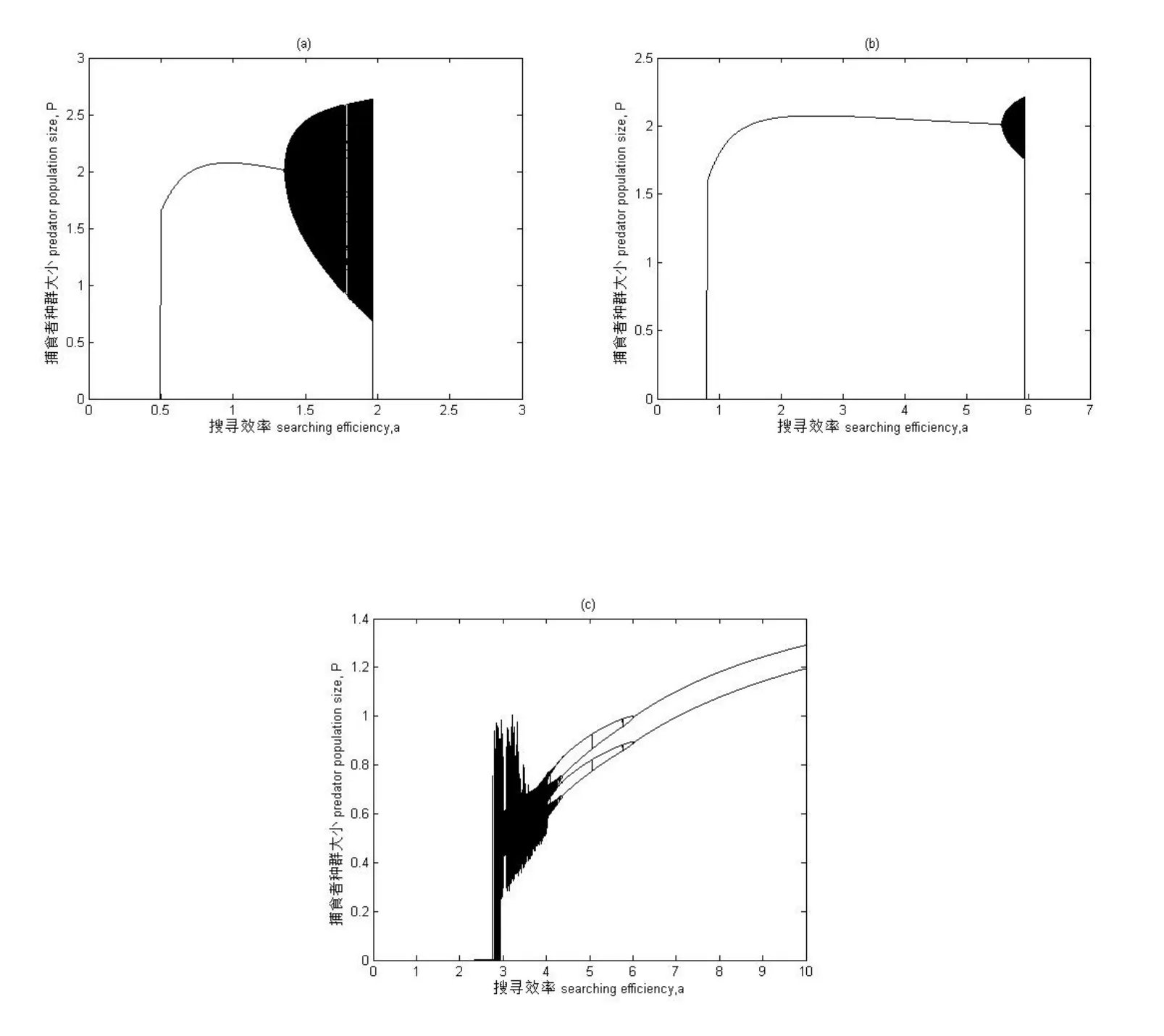
图 1 系统(2)分岔图 搜寻效率a为横坐标,捕食者种群数量大小P为纵坐标 参数取值为K=5,T=1,c=0.1,r=3,m=0.0002,系统初值为H0=5,P0=2.5.(a)Th=0.3(b)Th=0.5(c)Th=0.8.

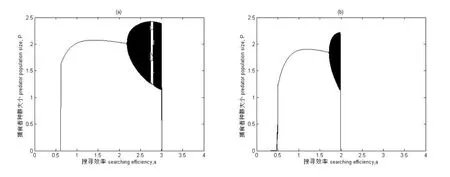
图 2 系统(2)分岔图 搜寻效率a为横坐标,捕食者种群数量大小P为纵坐标 参数取值为K=5,T=1,Th=0.4,系统初值为H0=5,P0=2.5. (a)c=0,m=0(b)c=0.1,m=0.5.

图3为同样为具有Allee效应和HollingⅡ型功能反应模型的分岔图.以捕食者的內禀增长率r为分岔图参数,即內禀增长率作为分岔图横坐标,其余参数取值为：K=5,a=2,T=1,Th=0.4,系统初值为：H0=5,P0=2.5.图3(a)为c=0,m=0时,捕食者种群的生长状态,从图中我们可以知道,在內禀增长率r取值为0.263时出现混沌状态,直到参数增长到2.251时种群出现稳定共存状态,并在(1.6,1.8)及(2.0,2.1)之间出现周期窗,周期变化形态颇为复杂.接着出现稳定共存的生长状态.图3(b)表现的是c=0.1,m=0.5时的捕食者种群的生长状态,相对于没有Allee效应的情况下来说生长状态较为复杂,在3.029之后出现混沌状态,参数在3.592之后一段参数区间内保持稳定共存,短暂共存状态后再次出现混沌状态,后种群突然灭绝.

3.3 Allee效应辅助参数对模型的影响

同样根据前面的探索选择一个相对合适的处理时间参数进行模拟讨论Allee辅助参数在具有Allee效应及HollingⅡ型功能反应模型的动态行为的影响.

图4为具有Allee效应和HollingⅡ型功能反应模型系统的分岔图.以捕食者的搜寻效率a为分岔图参数,其余参数取值为：K=5,r=3,m=0.5,T=1,Th=0.4,系统初值为：H0=5,P0=2.5.图4(a)为系统中参数取值c=0.1,即具有Allee效应的动态系统,该处的分岔图同图2中(b)部分.图4(b)为系统参数c=-0.02时的动态系统,稳定参数域扩大为(0.532,1.819),接着呈现混沌状态,混沌比较复杂,具有草叉分支、切叉分支、吸引子危机、拟周期变化,参数增大到3.321种群突然灭绝.

3.4 最大Lyapunov指数判断混沌动态

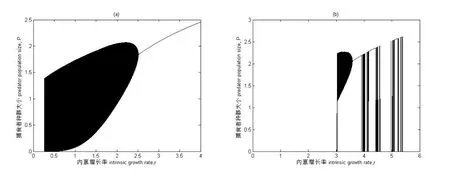
图3 系统(2)分岔图 內禀增长率r为横坐标,捕食者种群数量大小P为纵坐标 参数取值为K=5,a=2,T=1,Th=0.4,系统初值为H0=5,P0=2.5. (a)c=0,m=0(b)c=0.1,m=0.5.

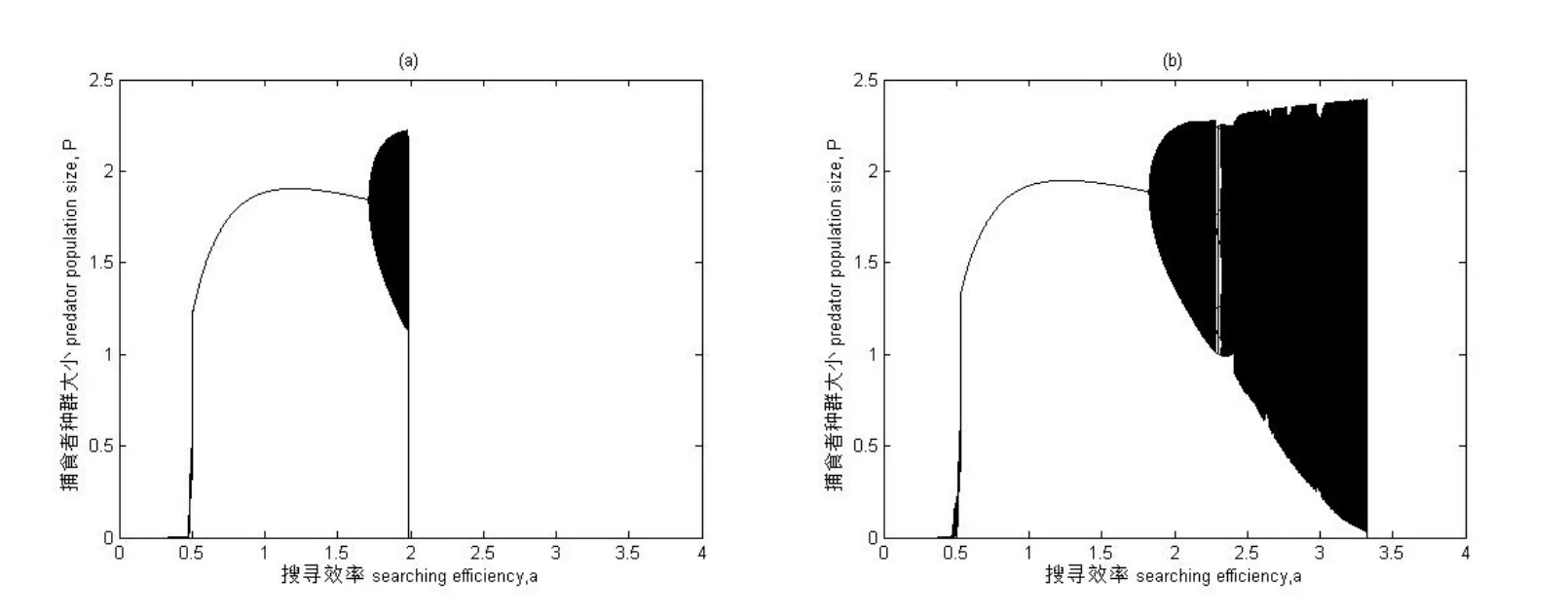
图4 系统(2)分岔图 搜寻效率a为横坐标,捕食者种群数量大小P为纵坐标 参数取值为K=5,r=3,m=0.5,T=1,Th=0.4,系统初值为H0=5,P0=2.5. (a)c=0.1(b)c=-0.02.

对于混沌状态[14]的判断只有直接的分岔图结论远远不够,本节采用求解最大Lyapunov指数的方法来从理论上支撑混沌状态的判断[15].最大Lyapunov指数计算即在相平面空间计算附近的轨道发散或者收敛的平均指数.下面完整叙述其计算过程：第一步,找到一个吸引子上的一个已知点x0,这个点对于任意的初始条件都可以迭代几百次,并有邻点y0使得d0=||x0-y0||,且d0=10-12.第二步,每两个轨道通过一次迭代可得xk,yk,由公式dk=||xk-yk||可计算出dk,其中k=1,2,···,n,dk6=d0.将上述两步进行n次迭代计算平均对数率.最后得到最大Lyapunov指数的计算式为对系统的最大Lyapunov指数的计算结果进行判断,若指数为正则为混沌状态,若为负则系统是稳定状态或者出现周期吸引子现象.图5为系统(2)的Lyapunov指数的计算结果,该图所对应的为图3,图4的局部参数域上的指数图像.对其余系统动态演化的分岔图均通过类似的方式对混沌状态进行理论验证,对每个参数作为讨论对象分别进行了混沌状态的Lyapunov指数的计算.

图5 系统(2)的最大Lyapunov指数 参数取值为K=5,T=1,Th=0.4,系统初值为H0=5,P0=2.5. (a)內禀增长率r为横坐标,最大Lyapunov指数L为纵坐标,a=2,c=0,m=0;(b)搜寻效率a为横坐标,最大Lyapunov指数L为纵坐标r=3,c=-0.02,m=0.5.

§4 结果分析

考虑捕食者对食饵攻击的攻击过程,通过计算机模拟参数内禀增长率r,搜寻效率a,Allee效应宿主阈值c,Allee效应常数m变化时种群的动态变化趋势.该动态变化过程以分岔图进行呈现,在分岔图中种群动态系统随参数变化会出现Hopf分支,混沌状态[16-20].对分岔图进行详细分析得到如下结论：

结论一,当处理时间在有效区间内变化时,处理时间越大种群的稳定共存参数域越大.如图1所示,当捕食者对猎物的处理时间在有效情况下：处理时间小于捕食过程的总时间的二分之一时,系统的种群大小的变化会随着参数的增加而处于特殊的变化,种群动态的整体变化趋势是类似的;而当处理时间增大至超过捕食总时间的二分之一时,种群的整体动态变化趋势发生变化,该部分种群生长状态中会出现倒转的倍周期增长.由图中我们可以得到结论,处理时间的增加在增大了种群存活参数域的同时也增大了两种群稳定共存的参数域.

结论二,在具有HollingⅡ功能反应的离散的食饵-捕食者系统中由于Allee效应的引入,增加了捕食者种群的灭绝风险.模拟结果显示去掉Allee效应能增加捕食者种群的续存.在图2和图3的软件模拟的结果中,可以很清楚的看到以a和r为参数,增加Allee效应参数m,模拟有Allee效应和没有Allee效应的情况下种群的生长动态.从图中我们可以通过对比分析当Allee效应参数c=0，m=0时和c=0.1，m=0.5时,种群生长状态的情况：当m=0.5时,种群稳定共存的参数域均发生了变化,搜寻参数的参数取值范围由a∈(0.619,2.172)变为了a∈(0.506,1.705),內禀增长率r稳定共存的参数域也由(2.251,4.249)缩小了.通过对分岔图进行具体分析,可知Allee效应增加了种群的动态复杂性加速了种群的灭绝.

结论三,当系统受强Allee效应影响时,将推迟出现混沌现象,也就是说强Allee更容易使种群产生分叉,即强Allee会使种群提前出现分叉现象,继续增强Allee效应,导致种群灭绝[21-22].而系统Allee参数取c＜0,系统还是会出现混沌现象.对于参数域中系统出现的混沌现象通过计算Lyapunov指数来对分岔图的混沌现象进行了理论支撑,就每个参数进行了对应的指数计算,文中第三部分的第四小节只就部分参数域进行了诠释.当Lyapunov指数大于0时出现混沌状态,小于0时则是稳定状态或者是一个周期吸引子.当Allee参数c＞0时为强Allee效应,如图4所示可以清楚的观察到当c=0.1时种群的混沌状态后出现分叉比c=-0.02时容易.从图中我们还可以看到当c=0.1时,考虑Allee效应的作用力度,继续增强Allee效应参数c将会导致种群存活的参数域缩短.相对于强Allee效应来说,参数c＜0时加强了种群的稳定性,两种群的稳定共存的参数域也因稳定性的加强而增大.

[1] Allee W C.Animal Aggregations：A Study in General Sociology[M].Chicago：University of Chicago Press,1931.

[2] Andrew L,Jordi B.The Allee e ff ect,stochastic dynamics and the eradication of alien species[J].Ecol Lett,2003,6：133-140.

[3] Zhou Shurong,Liu Yafeng,Wang Gang.The stability of predator-prey systems subject to the Allee e ff ects[J].Theor Popul Biol,2005,67：23-31.

[4] Zu Jian.Global qualitative analysis of a predator-prey system with Allee e ff ect on the prey species[J].Math Comput Simul,2013,94：33-54.

[5] Zhao Yanzhong.Study of a Class of Predator-Prey Di ff usive System with Allee E ff ect[J].College Math,2011,27(5).

[6] Gascoigne J,Lipcius R N.Allee e ff ects in marine systems[J].Mar Ecol Prog Ser,2004,269：49-59.

[7] Petrovskii S V,Morozov A Y,Venturino E.Allee e ff ect makes possible patch invasion in a predator-prey system[J].Ecol Lett,2002,5：345-352.

[8] Wang Wanxiong,Zhang Yanbo,Liu Changzhong.Analysis of a discrete-time Predator-prey system with Allee e ff ect[J].Ecol Complex,2011,8：81-85.

[9] Holling C S.Some characteristics of simple types of predation and parasitism[J].Can Entomol,1959,91：385-398.

[10]Holling C S.The function response of invertebrate predators to prey density[J].Mem Entomol Soc,1966,48：1-86.

[11]刘华,李自珍,刘志广,等.宿主-寄生物种群模型的复杂动态[J].兰州大学学报：自然科学版,2009,45(4)：53-59.

[12]Kumar S,Srivastava S K,Chingakham P.Hopf bifurcation and stability analysis in a harvested one-predator-two-prey model[J].Appl Math Comput,2002,129(1)：107-118.

[13]Zu Jian,WANG Wendi.Evolutionary dynamics of predator-prey systems subject to Allee e ff ects[J].J Southwest University(Natural Science Edition),2007,29(4)：14-21.

[14]Lv Songjuan,Zhao Min.The dynamic complexity of a three species food chain model[J].Chaos Solitons and Fractals,2006,10(57)：1-12.

[15]沈林,周红玲,李艳玲.一类具有弱Allee效应的捕食-食饵模型正解的存在性[J].西南大学学报：自然科学版,2012,34(7)：21-27.

[16]张琪昌.分岔与混沌理论及应用[M].天津：天津大学出版社,2005.

[17]Pan Xiaohong.Local Stability and Hopf bifurcation of a predator-prey model with Hollingtype II and Allee e ff ect[J].J Qufu Normal Univ,2012,38(3)：7-12.

[18]付晓阅,张玉娟,刘超,等.具有效应的食饵一捕食者模型的稳定性分析[J].生物数学学报,2012,27(4)：639-644.

[19]王静,薛亚奎.一类具有Allee影响的捕食与被捕食模型[J].数学的实践与认识,2008,38(10)：136-140.

[20]王万雄,赵灿省,张艳波.一类具有Allee效应的捕食系统的稳定性分析及模拟[J].数学的实践与认识,2013,43(20)：245-249.

[21] 高玉景.一类带有强Allee效应捕食-食饵系统的Hopf分支[J].兰州大学学报：自然科学版,2014,50(4)：564-568.

[22]臧辉,聂华.一类具有强Allee效应的捕食－食饵模型正平衡态解的存在性[J].陕西师范大学学报：自然科学版,2013,41(5)：5-10.

A predator-prey system model with Holling II functional response and Allee e ff ect

JIANG Rui1,LIU Hua1,XIE Mei1,WEI Yu-mei2,ZHAO Shifeng1
(1.School of mathematics and computer science Institute,Northwest university for nationalities,Lanzhou 730030,China;2.The experiment center,Northwest university for nationalities,Lanzhou 730030,China)

This paper studied the dynamic complexity of a class of discrete population model by computer simulation.The autonomous predator-prey system model is established through theoretical derivation,which has Allee e ff ect and Holling II functional e ff ect.The growth states of discrete-time populations are simulated to explore the in fl uence of the parameters’changes to its population size by MATLAB.It also illustrated the importance of Allee e ff ect and Holling II functional in the model of interaction among populations.The research results show that the larger the processing time,the bigger parameter region for stable coexistence population when the processing time is within the e ff ective range.The introduction of Allee e ff ect makes dynamic behavior of the population more complicated,thus increase the extinction risk of predator population.The population appears bifurcation in advance when predator-prey system strongly a ff ected by Allee e ff ect.It will lead to population extinction,if Allee e ff ect increasingly raises.The strong Allee e ff ect is more prone to population extinction.The conclusion of this paper not only enriches the theory of ecology,but also puts forward important basis of conservation ecology.

Allee e ff ect;Holling II;chaos;computer simulation

34B

O175

A

：1000-4424(2016)04-0441-10

2015-11-13

2016-03-23

国家自然科学基金(31260098;11361049;31560127);甘肃省自然科学基金(145RJZA158;1506RJZA274);西北民族大学研究生科研创新资助项目(YXM2015178);国家民委中青年英才计划([2014]121号);2013年西北民族大学创新团队资助项目