偏t正态数据下混合线性联合位置与尺度模型的参数估计

朱志娥,吴刘仓,戴 琳

(昆明理工大学理学院,云南昆明650093)

偏t正态数据下混合线性联合位置与尺度模型的参数估计

朱志娥,吴刘仓,戴 琳

(昆明理工大学理学院,云南昆明650093)

偏t正态分布是分析尖峰,厚尾数据的重要统计工具之一.研究提出了偏t正态数据下混合线性联合位置与尺度模型,通过EM算法和Newton-Raphson方法研究了该模型参数的极大似然估计.并通过随机模拟试验验证了所提出方法的有效性.最后,结合实际数据验证了该模型和方法具有实用性和可行性.

偏t正态分布;混合线性联合位置与尺度模型;EM算法;极大似然估计

§1 引 言

在社会经济领域中,经常收集到的数据存在着大量分类问题且不是严格地服从正态分布,而是服从具有明显偏斜的厚尾分布.面对这些情况,如果简单的对数据总体进行分析,那么就很难找到数据中各类别的差异.因此,为了更好的分析数据的特征,常常对数据进行聚类分析.聚类分析是将总体数据按不同指标或特性进行分类,再对具有相似性质或相似指标的数据进行详细的分析,这使得在研究大数据时减少了很多工作量.一方面,偏t正态分布能够较好的刻画具有明显偏斜和厚尾数据的分布规律.另一方面,了解是哪些因素影响了数据出现偏斜和厚尾的情况,这一问题也是研究者们所关注的热点.因此,对偏t正态数据的统计分析具有重要的理论价值和实际意义,本文主要研究偏t正态数据下混合线性联合位置与尺度模型的参数估计问题.

混合回归模型是研究含有两个及两个以上子聚类的混合数据的最重要的统计分析工具之一,在经济学、医学、环境科学、生物学、抽样调查及工程技术等领域具有广泛的应用.自Goldfeld和Quandt[1]首次介绍了混合回归模型以来,混合回归模型就吸引了很多研究学者的关注,可参见McLachlan和Peel[2]的专著及其里面的参考文献.最近,Yao等[3]基于t分布研究提出了稳健的混合线性回归模型;Song等[4]基于Laplace分布研究提出了稳健的混合线性回归模型;Azzalini[5]系统地对偏正态分布的性质进行了研究;Kotz和Vicari[6]综述了偏态分布的研究现状;Nadarajah等[7]也讨论了一系列偏态分布及其各自的性质,并求得了这些分布的特征函数和n阶矩的表达;Liu和Lin[8]基于偏正态分布,首次研究了偏态数据下混合线性回归模型.

以上所研究的数据特征仅为偏斜或厚尾,并未同时对具有偏斜和厚尾的数据进行研究,且以上研究都假定混合数据的每个子聚类的方差都相同,偏度也相同.然而,在许多实际问题中这样的假定是不合理的.针对异方差数据,很多统计学者对联合均值与方差模型进行了系统的研究.如吴刘仓等[9]研究了偏t正态数据下联合位置与尺度模型的极大似然估计;Aitkin[10]给出了联合均值与方差模型的极大似然估计;吴刘仓等[11]研究了联合均值与方差模型的变量选择.此外,G´omez[12]针对偏t正态模型讨论了其极大似然估计方法和Fisher信息矩阵及其相关性质;吴刘仓等[13]研究了缺失偏t正态数据下线性回归模型的参数估计;Lin等[14]研究了偏t正态数据下非线性回归模型中方差的齐次性检验.然而,针对混合偏态异方差数据研究较少.

故本文针对偏t正态混合数据、异方差和线性回归,提出了偏t正态数据下混合线性联合位置与尺度模型.其次利用EM算法和Newton-Raphson方法研究此模型参数的极大似然估计.最后,结合实际数据说明该模型和方法具有实用性和可行性.

本文由以下几个部分构成：§2首先简要的介绍偏t正态分布及其密度函数的表示,在其基础上提出了偏t正态数据下混合线性联合位置与尺度模型;§3详细的介绍了偏t正态数据下混合线性联合位置与尺度模型的EM算法,并给出了此模型下EM算法的操作步骤;§4通过随机模拟试验验证了该方法的有效性;§5结合实际数据说明了该模型和方法的实用性和可行性;§6是本文的小结和讨论.

§2 偏t正态数据下混合线性联合位置与尺度模型

2.1 偏t正态分布

偏t正态分布实际是一种广义的正态分布.考虑随机变量Y服从StN分布,同G´omez[12]一样,即可以表示成Y ∼StN(µ,σ2,λ,ν),其中,µ为位置参数,σ 为尺度参数,λ为偏度参数,ν为自由度,随机变量Y的概率密度函数可表示为：

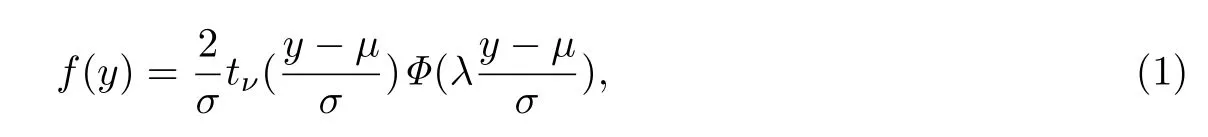
其中,tν(·)为自由度为ν的t分布的概率密度函数,Φ(·)为标准正态分布的分布函数.显然,当自由度ν→∞时,概率密度函数(1)即为SN分布的概率密度函数,当偏度参数λ=0时,将得到自由度为ν的t分布的概率密度函数.当自由度ν→∞和λ=0时,该分布为正态分布.在本文中,只考虑自由度ν是有限的情况.当自由度未知时,可通过截面似然的方法来对其进行估计.在偏t正态分布中,有

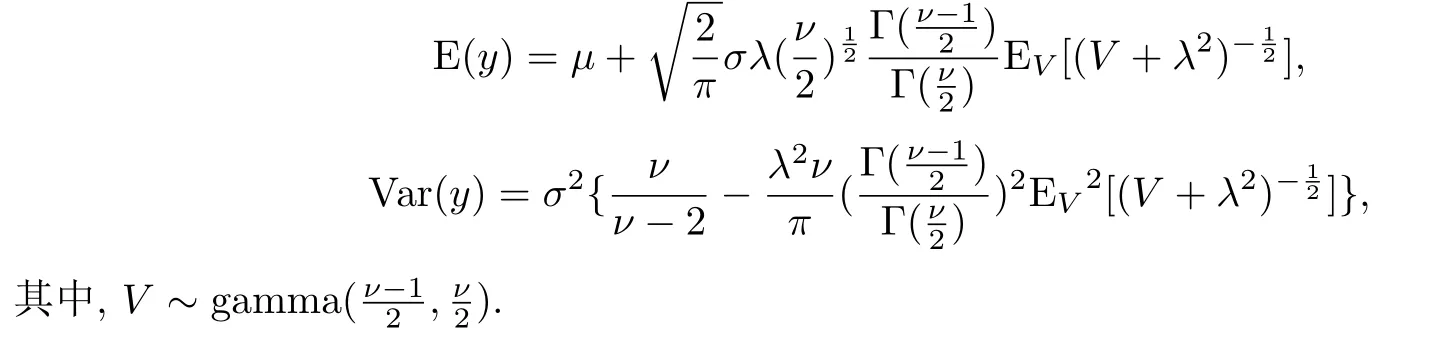
2.2 偏t正态数据下混合线性联合位置与尺度模型

设y1,y2,...,yn是n个来自m个混合比例为π1,π2,...,πm的随机样本量,概率密度函数为f(y)=StN(µ,σ2,λ,ν),即Y 服从混合偏t正态分布,

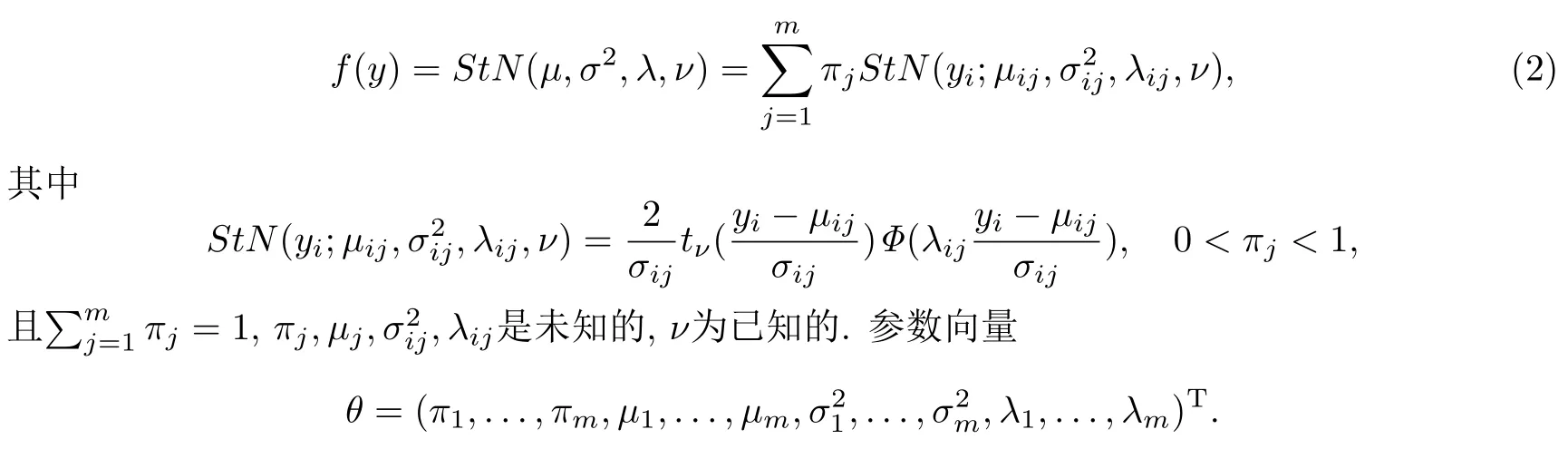
本文中,假定混合子聚类数m是固定和已知的.当然,在一些实际应用中,m可能是未知的,它也需要和混合比例以及其它参数一起估计,但在本文中,为了简化，仅考虑是m已知的情形,只对未知参数θ进行估计.

本文针对偏t正态混合数据,异方差和线性回归,提出如下偏t正态数据下混合线性联合位置与尺度模型：

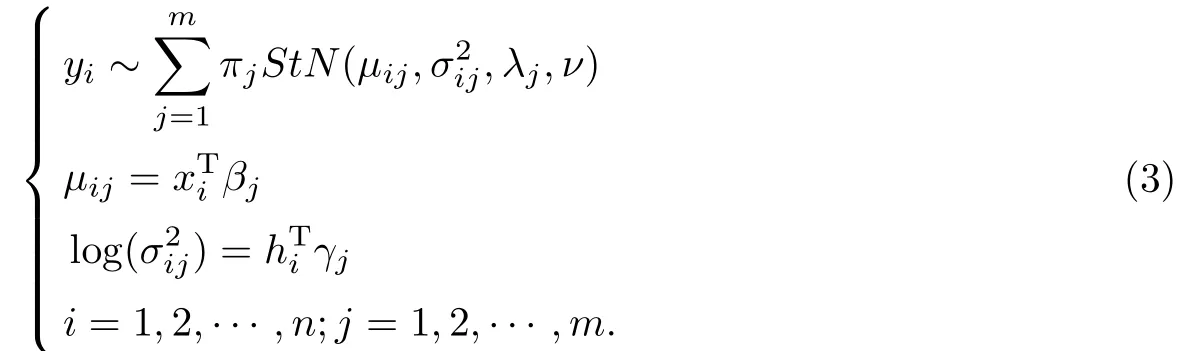
在模型(3)中,{yi}1是独立的响应变量,xi={xi1,...,xip}T和hi={hi1,...,hiq}T是解释变量,βj={βj1,...,βjp}T是第j个子聚类中维数为p×1的位置模型的未知参数,γj={γj1,...,γjq}T是第j个子聚类中维数为q×1的尺度模型的未知参数,λj是第j个子聚类的偏度参数.两个解释变量可能完全相同,部分相同或者完全不同,即位置模型和尺度模型可能包含一些相同的解释变量或者包含不同的解释变量.即使包含相同的解释变量也可能分别对位置模型和尺度模型产生不同的影响.

§3 偏t态数据下混合线性回归模型的EM算法

Mclachlan和Peel[2]指出EM算法可以获得有限混合模型任意分布的极大似然估计.本文假定子聚类m是固定和已知的,由于每一次观测值都属于m个子聚类中的一类,但无法确定是m类中的第几类.为了解决这个问题,引入潜变量zi=(zi1,...,zim),

对不可确定来自m类中的第几类的情况,可以利用多项式分布zij进行刻画,若yi属于m个子聚类中的第j类,则zij等于1,若yi不属于m个子聚类中的第j类,而属于m-1类中的某一类,此时zij等于0. 则完全数据下关于参数的对数似然函数可以写成：

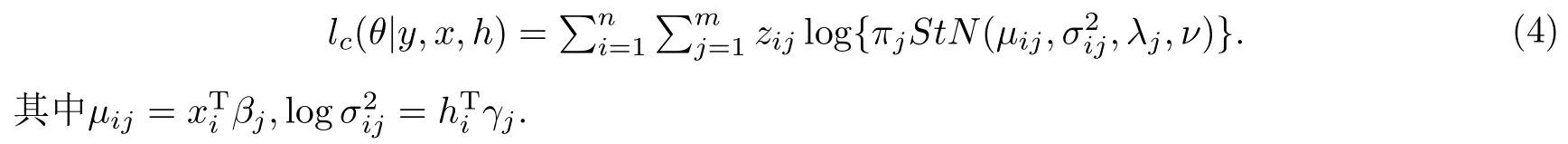
EM算法(Expectation Maximization Algorithm)是一种聚类算法,其具体流程分为两个步骤进行：E-step和M-step.第一步,E-step是根据参数初始值或上一次迭代所得结果来计算对数似然函数的期望值;第二步,M-step是将对数似然函数最大化以获得新的参数值,用新得到的参数值代替初始值或上一次迭代所得结果使得对数似然函数最大化.重复执行以上两步骤,直至收敛.

下面给出EM算法在偏t正态数据下混合线性联合位置与尺度模型中的计算步骤：E-step：利用从k次迭代得到的估计θ(k),计算出：

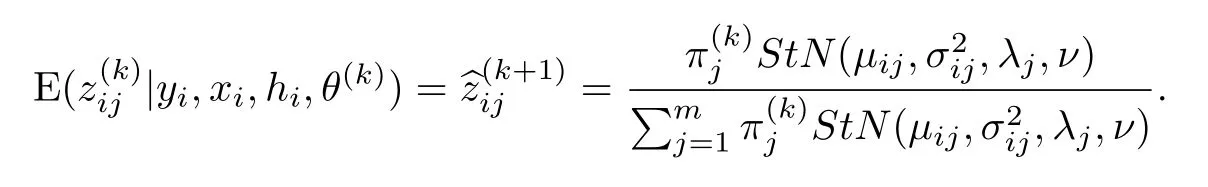
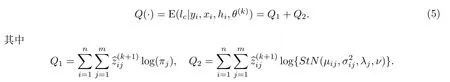
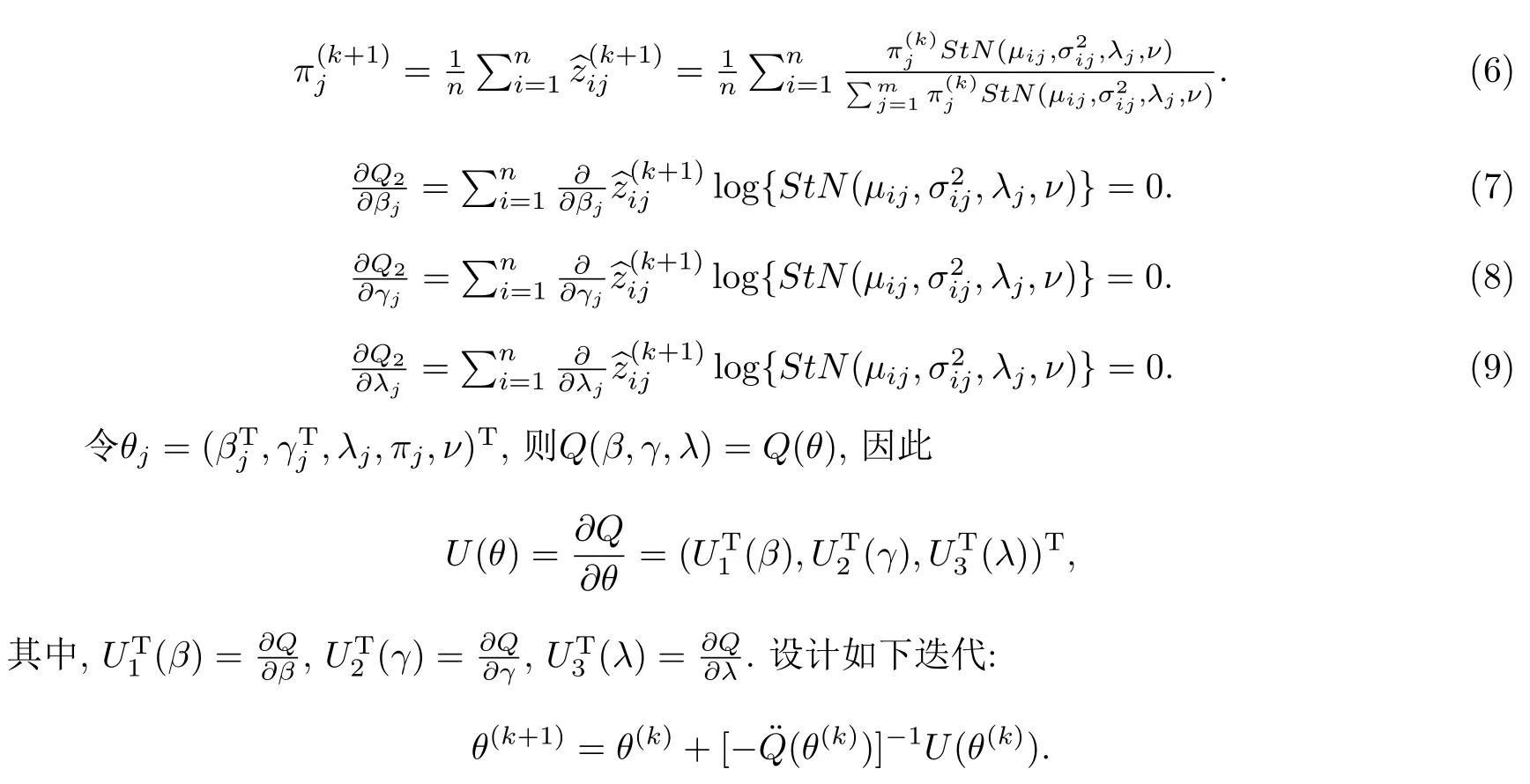
EM算法的操作步骤：

步骤2：E-step,在k+1次迭代中,通过引入潜变量zij来确定来自m类中那一类的数据,然后计算完全数据下对数似然函数的条件期望：

步骤3：M-step,在k+1次迭代中,使用下面的公式进行最大化的计算：

利用Newton-Raphson方法能得出θ的极大似然估计.

步骤4：重复步骤2和步骤3,直至收敛.

当自由度ν未知时,可以通过最大化对数似然函数将自由度ν和混合回归模型参数θ一起估计出来.为了简化,也可以考虑ν的截面最大似然(Pro fi le likelihood)估计：

红松是国家保护植物，其物种的价值珍贵，工业，农业，城市建筑和室内装饰。因此，植树造林工程栽培受到重点关注。松树造林工程保护自然资源和生态环境，但也产生经济效益的，造林工程项目，对造林工程技术的高要求。

注：一方面,因为偏t正态分布是单峰的;另一方面,当|θ(k)-θ(k-1)|≤δ,δ为预定的充分小的正数,如δ=10-3等,保证了EM算法的收敛.

§4 Monte Carlo模拟

为了评价上述参数估计方法的有效性,对有限样本性质进行模拟研究,参数估计的精确度使用均方误差(MSE)来评价和衡量,其定义如下：

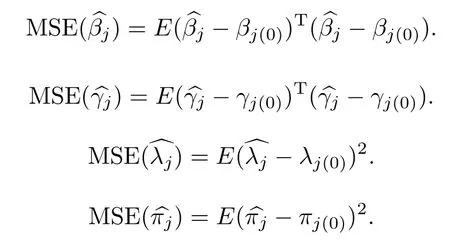
其中βj(0),γj(0),λj(0),πj(0)分别是βj,γj,λj,πj的真值.

根据下面的模型(10),产生模拟数据：

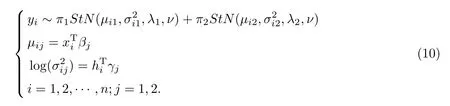
其中yi(i=1,2,...,n)是根据StN分布混合产生的相互独立的响应变量,且yi服从偏t正态分布.xi∼U(-1,1),hi∼U(-1,1)是各自分量相互独立的解释变量,分别取π1(0)=0.25和0.50由π2=1-π1可知：π2(0)=0.75和0.50给定β1,γ1,λ1和β2,γ2,λ2的真值分别为：β1(0)=(0,1,1)T,γ1(0)=(0,1,1)T,λ1(0)=0.5,β2(0)=(0,-1,-1)T,γ2(0)=(0,-1,-1)T,λ2(0)=-0.5 取样本量n=400,600,800,分别取ν=3,4,5,重复模拟1000次.通过1000次模拟的均方误差的平均数评价和衡量参数估计的精度,模拟结果见表1,表2和表3.根据表1,表2和表3的模拟结果,可得到,无论样本是左偏或者右偏,即偏度参数λ取负值或者正值：

表1 ν=3的模拟结果

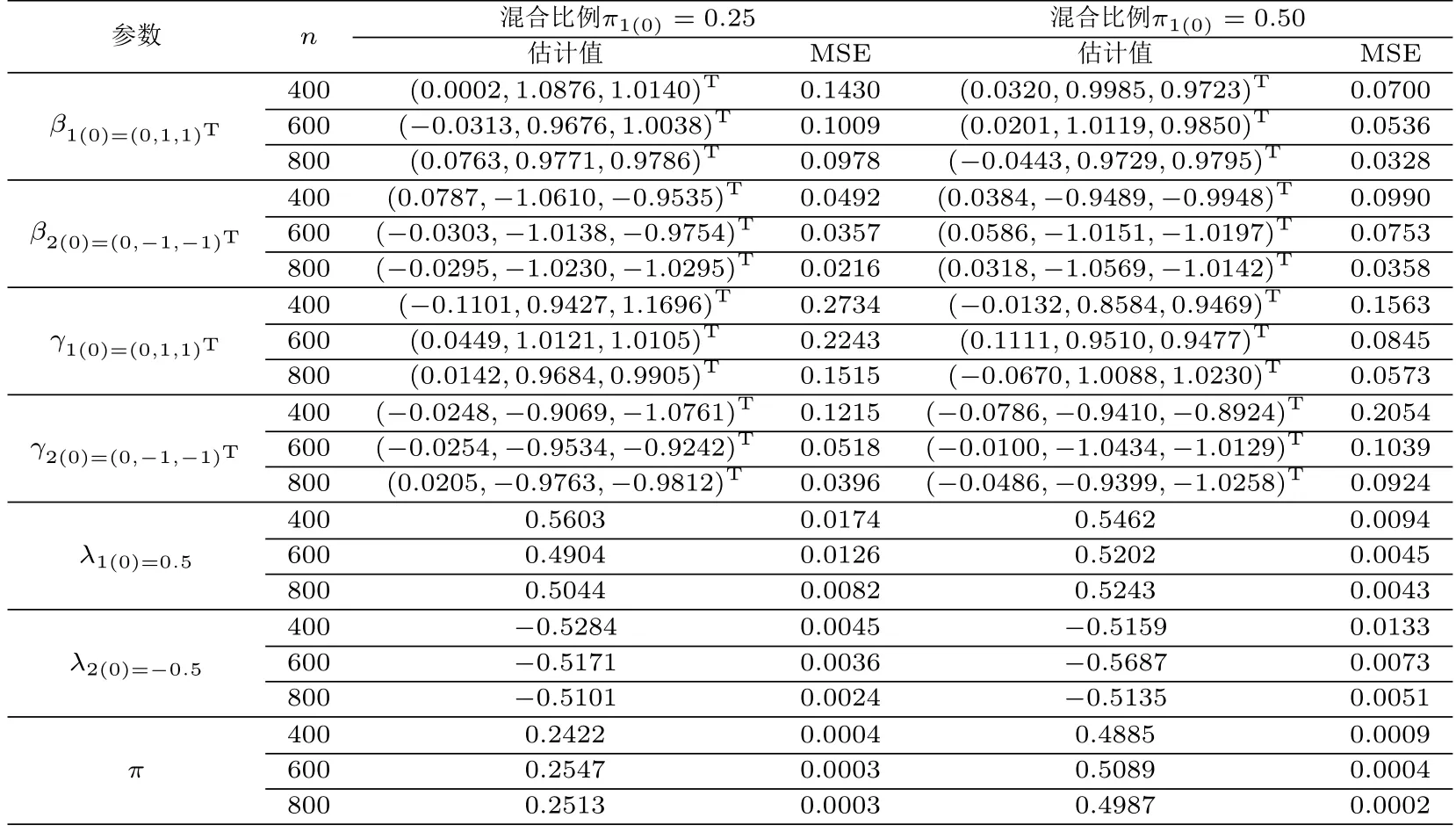
表2 ν=4的模拟结果

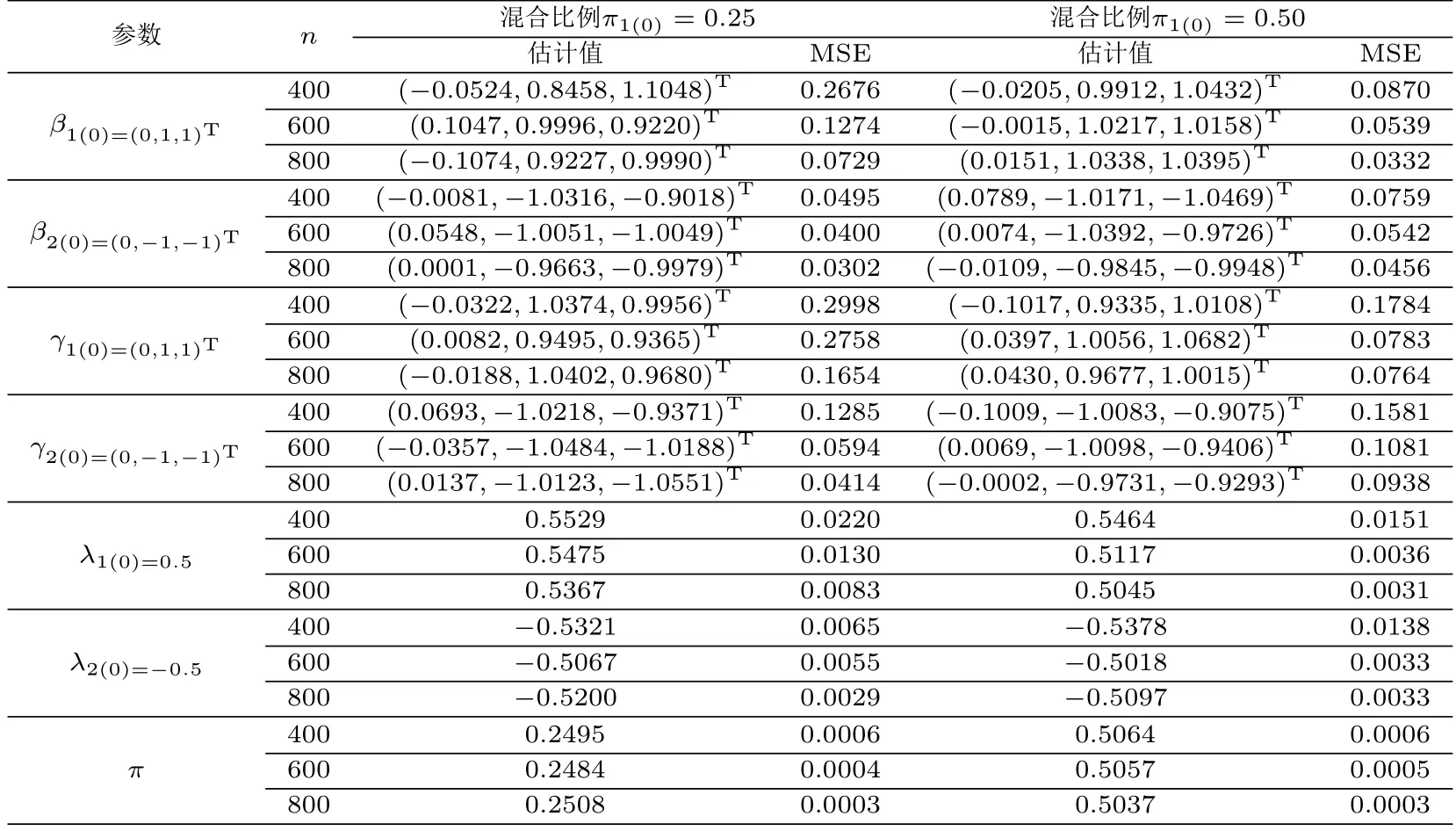
表3 ν=5的模拟结果

(1)在相同的自由度ν下,随着样本量n的增加所有参数的估计值越来越接近真值,且估计的均方误差MSE也越来越小.

以上结论表明,本文基于偏t正态数据提出的混合线性回归模型及所使用的EM算法对参数的极大似然估计取得了较理想的效果.

§5 实例分析

下面利用本文提出的偏t正态数据下混合线性联合位置与尺度模型及其方法,对运动员体质指数数据进行统计推断.

人体体质指数(BMI)是衡量一个人是否肥胖或超重的标准之一.采用202名运动员的体质指数(BMI)数据[16]进行统计分析,其中女性运动员100名,男性运动员102名.体质指数(BMI)包含有响应变量Y-kg/(cm)2和8个解释变量：X1-红细胞计数,X2-白细胞计数,X3-比容,X4-血红蛋白X5-等离子铁蛋白浓度,X6-总皮肤褶皱,X7-体脂百分比,X8-去脂体重.将建立体质指数Y(BMI)与8个解释变量之间的关系.(这里假定xi与hi相同).

首先,对体质指数(BMI)数据进行正态性检验,并作出直方图与QQ图,见图1,图2及图3,且分别为全部202名运动员,100名女性运动员和102名男性运动员的体质指数(BMI)的正态检验的概率图.从以下这三幅图可直观上看出,数据近似服从正态分布,但具有明显的偏斜,且均值附近与尾区的概率值比正态分布大,而其余区域的概率比正态分布小,即所研究数据具有尖峰、厚尾的特征.

图1 202名运动员的体质指数(BMI)的直方图与QQ图

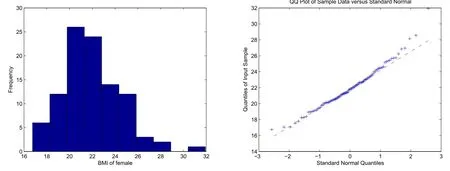
图2 100名女性运动员的体质指数(BMI)的直方图与QQ图

利用模型(10),建立如下模型：

表4 体质指数BMI参数的估计结果

从表4中可以得出：对于三组数据所建立的联合位置模型和尺度模型有细微的差异.解释变量X1-红色细胞计数,在联合位置模型和尺度模型中对女性体质指数的影响较小,对混合数据和男性数据的影响成一致关系;在两个模型中解释变量X3-比容,对混合数据和女性数据的影响成一致关系;在尺度模型中解释变量X7-体脂百分比,对混合数据成正影响,而对男性数据和女性数据成负影响.若不考虑分类研究,其结果可能会偏离实际影响,从而得到错误的结论.表4所得到的精细结果能为进一步深入研究体质指数(BMI)提供了重要的统计保障.

§6 结论

本文基于混合偏t正态数据,异方差和线性回归,研究提出了偏t正态数据下混合线性联合位置与尺度模型,并利用EM算法和Newton-Raphson方法研究了该模型参数的极大似然估计.Monte Carlo随机模拟结果表明模型参数估计方法有效和可行.通过对运动员体质指数(BMI)实际数据的分析也说明了该模型和方法具有实用性.

参考文献：

[1] Goldfeld S M,Quandt R E.A Markov model for switching regression[J].Journal of Econometrics,1973,1：13-16.

[2] McLachlan G,Peel D.Finite Mixture Models[M].New York：Wiley，2000.

[3] Yao Wenxin,Wei Yan,Yu Chun.Robust mixture regression models using t-distribution[J].Computational Statistics and Data Analysis,2014,71：116-127.

[4] Song Weixing,Yao Wenxin,Xing Yanru.Robust mixture regression models fi tting by Laplace distribution[J].Computational Statistics and Data Analysis,2014,71：128-137.

[5] Azzalini A.A class of distributions which includes the normal ones[J].Scandinavian Journal of Statistics,1985,2：171-178.

[6] Kotz S,Vicari D.Survey of developments in the theory of continuous skewed distributions[J].International Journal of Statistics,2005,2：225-261.

[7] Nadarajah S,Kotz S.Skew distributions generated from di ff erent families[J].Acta Applicandae Mathematica,2006,91：1-37.

[8] Liu Min,Lin Tsung-I.A skew-normal mixture regression model[J].Educational and Psychological Measurement,2014,74：139-162.

[9] 吴刘仓,马婷,戴琳.基于StN分布下联合位置与尺度模型的极大似然估计[J].应用数学,2013,26：671-676.

[10]Aitkin M.Modelling variance heterogeneity in normal regression using GLIM[J].Applied Statistics,1987,36：332-339.

[11]吴刘仓,张忠占,徐登可.联合均值与方差模型的变量选择[J].系统工程理论与实践,2012,32：1754-1760.

[12]G´omez H W,Venegas O,Bolfarine H.Skew-symmetric distributions generated by the distribution function of the normal distribution[J].Environmetric,2007,18：395-407.

[13] 吴刘仓,张家茂,李玲雪.缺失偏t正态数据下线性回归模型的统计推断[J].应用数学,2015,28：16-25.

[14]Lin Jinguan,Xie Fengchang,Wei Bocheng.Statistical diagnostics for skew-t-normal nonlinear models[J].Communications in Statistics-Simulation and Computation,2009,38：2096-2110.

[15]Taylor and Francis.Finite mixture of generalized semiparametric models variable slection via penalized estimation[J].Communications in Statistics-Simulation and Computation,2015,DOI：10.1080/03610918.2014.953687.

[16]Cook A D,Weisberg S.An introduction to regression graphics[M].John Wiley Sons,1994.

Parameter estimation for linear joint location and scale models with mixture skew-t-normal data

ZHU Zhi-e,WU Liu-cang,DAI Lin
(Faculty of Science,Kunming University of Science and Technology,Kunming 650093,China)

Skew-t-normal distribution is one of the most important statistical tools to analyze the obvious peak and fat tail data.A linear mixture joint location and scale model with skew-t-normal data is proposed in this paper.The maximum likelihood estimation of the unknown parameters of this model is investigated based on Expectation Maximization(EM)algorithm and Newton-Raphson method.Furthermore,the proposed procedure works satisfactorily through Monte Carlo experiments.Finally,a real example shows that both this model and method are useful and e ff ective.

skew-t-normal distribution；mixture of linear joint location and scale models；EM algorithm；maximum likelihood estimation

62F10;62J12

O212.1

A

：1000-4424(2016)04-0379-11

2016-03-24

2016-04-26

国家自然科学基金(11261025;11026309);云南省自然科学基金(2011FZ044)