带损伤弹性反问题的数值分析

郑 聪,程晓良,梁克维

(浙江大学数学科学学院,浙江杭州310027)

带损伤弹性反问题的数值分析

郑 聪,程晓良,梁克维

(浙江大学数学科学学院,浙江杭州310027)

考虑一类由椭圆性方程和热传导方程共同来刻画的准静态弹性模型,通过给定观测值来反演边界的牵引力.首先构造一个凸目标泛函,并引入Tikhonov正则化方法,使之极小化得到一个稳定的近似解.再用有限元离散求解,导出误差估计.最后,用数值例子说明算法的可行性和有效性.

变分不等式;有限元方法;误差估计;数值模拟

§1 引 言

在日常生活和工业进程中,材料的损伤随处可见.损伤可能会导致材料结构发生变化,致使物体的承载能力降低甚至丧失.因此,在工程应用中,了解材料损伤的演变过程是非常重要的.

弹性正问题是在本构方程,材料特性,完整的边界条件和初始条件的已知情况下,求解位移场和损伤场.然而实际情况中,经常需要通过易测的(部分)位移信息来反求边界上(无法测量)的牵引力.这就是反问题.大多数反问题都是病态的,即解的存在性、唯一性和稳定性不能同时满足[1].因此,在求解病态问题上,通常会用到最小二乘[2],正则化[1,3-4]等方法,其中正则化方法包括迭代正则化,截断奇异值分解和Tikhonov正则化等.

关于形变反问题的研究成果并不太多.早期有用有限元方法来研究边界重构问题[5-6].后来,学者们引入正则化方法求解超定边界条件的问题[7-8].以及用边界元方法来求解形变反问题[8-9].而上述提及的研究都不考虑材料损伤情况.在[10]中,作者们考虑了材料的损坏情形.损伤变量用分片常数表示,通过边界信息来反求整个区域中的损坏部分.

本文考虑的是带损伤的弹性反问题,其中损伤变量满足特定的热传导方程.本文的目标是根据观测值(ud,βd),来求解稳定的牵引力f.首先用优化控制问题的思想来刻画这个问题,并保证解的存在性[11],同时引进Tikhonov正则化方法确保解的稳定性.最后利用对偶问题来构造可行的数值算法.

本文的结构如下.§2介绍一些符号和预备知识.§3阐述弹性正问题模型及其变分形式.§4给出相应的反问题和解的存在性,同时引入Tikhonov正则化方法来证明解的唯一性,并阐述解的收敛性.§5用有限元离散问题,并推导误差估计.§6给出可行算法,并进行二维数值模拟.

§2 符号及预备知识

设Sd表示Rd(d∈N)上的二阶对称张量空间.在Rd和Sd空间上,定义如下的内积和范数.

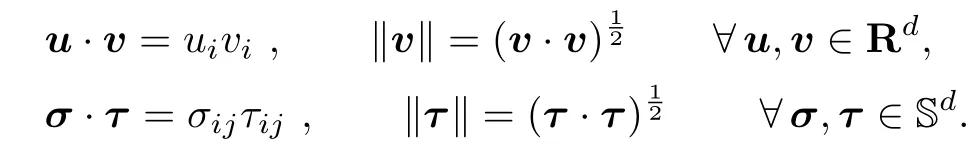
本文中,若无特别声明,i,j,k,l的取值都从1到d.接下来给出模型涉及的一些通用符号(详见[12]).设Ω ⊂Rd(d=1,2,3)是有界区域,且边界Γ是Lipschitz连续的.设ν=(νi)是Γ上的单位外法向量.将边界Γ分成两个不相交部分Γ1和Γ2,满足meas(Γ1)＞ 0,meas(Γ2)＞ 0,并且Γ2是闭的,物理模型的设置如图1(a)所示.记

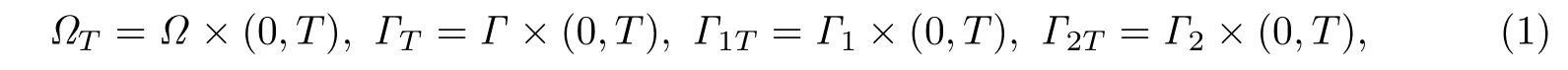
并定义如下6个空间：

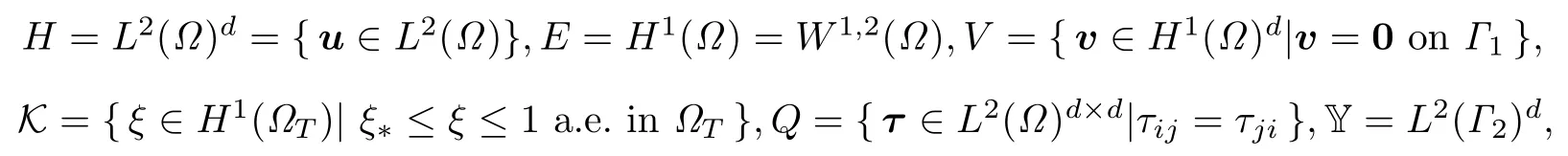
其中V和Q上的内积为：

§3 本构模型及其变分形式

考虑损伤源函数[13]：

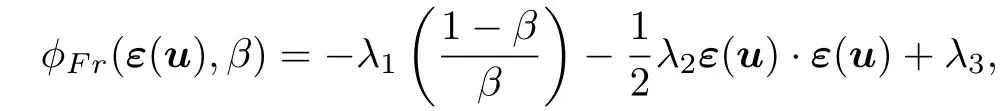
其中λ1,λ2和λ3是工艺参数,β是损伤变量.右边的第二项与弹性应变能量成正比,第三项是初始损伤的能量阈值.文献[14]指出太大的应变张量,不但在理论分析上会变得无法控制,而且会导致损伤模型无效.为了避免这个困难,引用如下的损伤原函数：

因为‖u‖V=‖ε(u)‖Q,所以弹性体的损伤变量关于位移是单调递减的(如图1(b)).在图1(b)中影响曲线形状的参数是由材料本身决定的[15-16].本文只考虑损伤变量函数β(u)是凸函数的情况.通过以上预备知识,弹性体准静态演化的经典模型(详见[14])表述如下.

问题 PM：求位移u(x,t)：ΩT→Rd,应变张量σ(x,t)：ΩT→Sd,损伤β(x,t)：ΩT→R

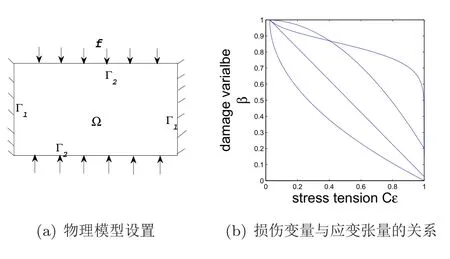
图1 物理模型设置及损伤变量与应变张量的关系

在研究问题(4)-(10)时,假设损伤源函数、弹性算子与应变张量满足如下关系.•条件(A)：弹性算子A：Ω×Sd→Sd是一个有界的四阶正定张量,满足：

•条件(φ)：损伤源函数φ：Ω×Sd×R→R是Lipschitz的,满足：

设牵引力和其他初始条件满足如下正则化条件[17]：

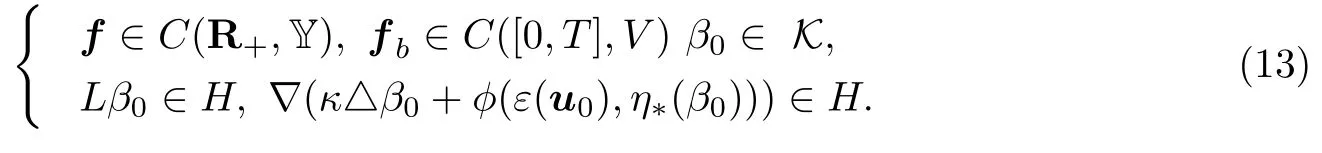
引进记号：

其中,算子A ：(0,T)× Ω → V∗,L ：E → E∗和(V∗,‖·‖V∗)是V的对偶空间.于是弹性问题PM的变分问题是：

问题PV：求u∈V,β∈K,满足,

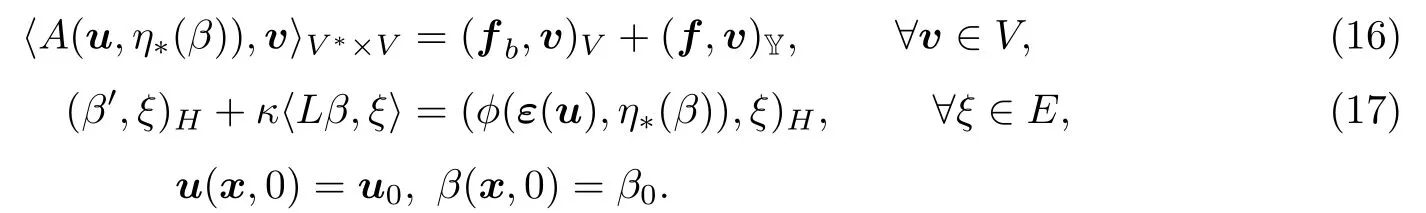
首先给出解的一致有界性和损伤变化量与位移变化之间的关系.

引理3.1.假设条件(11)-(13)满足,则问题PV存在唯一解.同时,对于给定的力f和fb,有

其中C1是不依赖于u,f的常数.

证 问题PV解的存在性和唯一性的证明是基于椭圆变分不等式和不动点方法,证明细节参见[12,14].由条件(A),(3)和(13),有

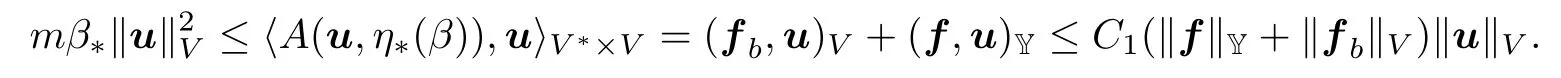
所以,不等式(18)得证.

§4 反问题

本节考虑弹性反问题,即在Γ2上,找一牵引力f,满足：(

其中,(uf,βf)是问题(4)-(10)的解,(ud,βd)是T时刻给定的观测数据.一般地,反问题难以直接求解.考虑下面问题.

问题IP1：求∈Yad,满足：

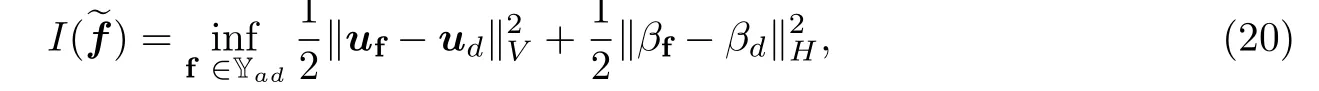
其中Yad是Y的闭凸子集,(uf,βf)是问题PV的解. 仍然用f来表示问题IP1的解(或准解),S表示准解集[1].

定理4.1.([13],定理19.3)假设条件(11)-(13)成立,则问题IP1至少有一个解.

由定理4.1,对于任何f∈S,用uf∈V表示问题PV的弱解.它的解不一定唯一,为此,对问题IP1引入Tikhonov正则化.

问题IP2：求fα∈Yad,满足：

引理4.1.对于α＞0,Jα(·)是严格凸的.

对于L,因为(u,β)是问题PV的解,则含有w,θ的项均为零,所以有Jα(f)=L(f,w,θ). 因此两边同时求导,有

命题4.1.对于∀α＞0,问题IP2存在唯一解fα∈Yad,而且fα可以被下面不等式约束：

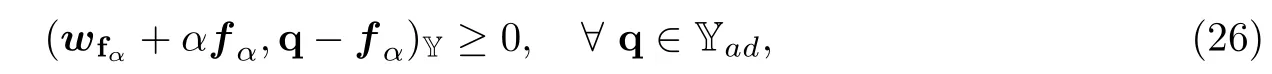
其中(wfα(x,t),θfα(x,t)) 是问题PDM的解.

证 因为Yad是Hilbert空间Y的一个闭凸子集,Jα(·)是严格凸的,所以,由凸优化理论可得,问题IP2存在唯一的稳定解fα∈Yad[18].而且这个解被下面优化条件所约束：

又因为(25)式,所以不等式(26)成立.

由定理4.1可知,问题IP1至少有一个解,所以S 6=∅.另外,易知S是一闭凸集.记由f∗是S中的唯一函数,满足：‖f∗‖Y=inff∈S‖f‖Y.当α → 0+时,有如下关于fα的结论.

命题4.2.当α → 0+时,fα→ f∗∈ Y.

证 设uf∗(f∗∈ S)是问题(4)-(10)的解.由(21)式,有

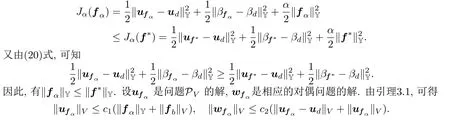
所以,fα,ufα,wfα和θfα分别在各自空间都是关于α一致有界.因此,存在f0,wf0,θf0,uf0和α的子序列{α′},当α′→ 0+时,有如下收敛关系：fα′⇀ f0,ufα′⇀ uf0,wfα′⇀ wf0,θfα′⇀ θf0.将不等式(26)中α换成α′,并由上述收敛关系可知,当α′→0+时,可得

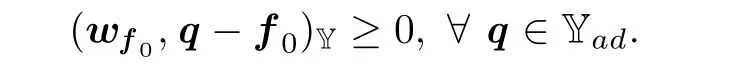
这表明f0是α=0时问题IP2的解,当然,也是问题IP1的解.所以f0∈S,且满足

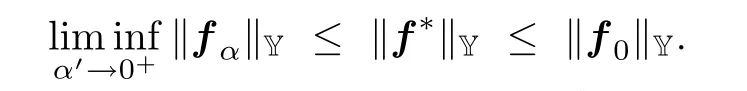
因此,f0=f∗.因为极限f0是唯一的,当α→0+,簇fα弱收敛到f∗.所以,当α→0+,有

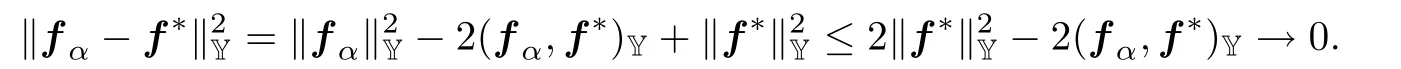
§5 数值离散及误差分析

首先考虑用两个有限维空间Vh⊂V和Eh⊂H分别来近似V和H空间.h＞0表示空间离散参数.假设Ω是一个多边形区域,Vh和Eh分别由连续和分段的仿射函数构成,即

通过同样的方法,利用‖u‖V=‖ε(u)‖Q,并考虑上述位移集合,可得

§6 优化算法及数值模拟

6.1 迭代优化算法

算法 6.1重构f的优化算法输入：(ud,βd)测量数据;ϵ＞0停止标准;1：初始化：f0α=0,k=1.2：当‖δfkα‖ ＜ ϵ,退出;否则执行3：已知fk-1α ,解问题PhV,得(uk,βk).4：令(uh,βh)=(uk,βk),解问题PhVD,得wk.5：计算δfkα=-wk/α,然后更新fkα=fk-1α+δfkα._6：令k:=k+1,返回第2步.

6.2 数值模拟

为了检验算法6.1的有效性,给出三种例子来观察弹性体在不同平衡状态和不同噪声水平下的数值结果.首先,算法的初值不依赖于观测数据(ud,βd),也并没有什么特殊要求.因此,为了简单,f的所有初始猜测都取为零向量.其次,所有例子都采用两套网格：粗网格(20×10)和细网格(40×20),而时间间隔上,统一采用Δt=0.1,其他参数和数据统一如下：

网格区域：Ω=(0,L1)×(0,L2),L1=2m,L2=1m.

边界：Γ =Γ1∪Γ2,

图2 重构f得到的弹性体的平衡状态和损伤分布：第一行图是重构f(48),第二行图是重构f(49).右列图表示在T=1s时刻的损伤分布.左列黑线区域表示弹性体的初始位置,红线区域表示平衡状态时的位置.采用的网格是黑色区域的一致三角网格.

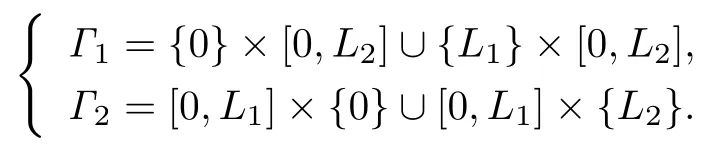
弹性张量算子A满足：

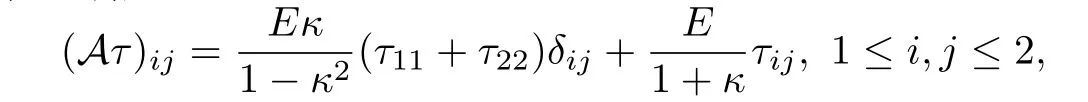
其中E是Young’s modulus,κ是材料的Poissons ratio,δij是Kronecker符号.

在数值实验中用到的其他数据：

例6.1.真解

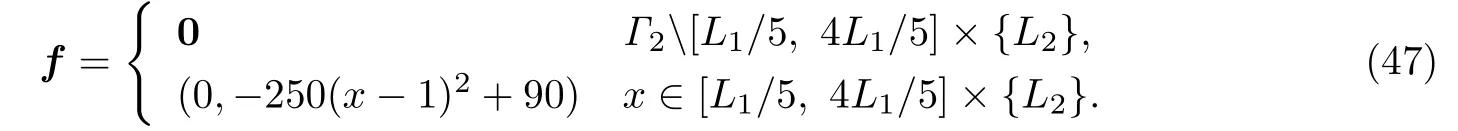
第一个实验是重构牵引力f(47).物体平衡状态和损伤分布的结果类似图2的第一行.在图2的左列,黑线区域表示弹性体的初始位置,红线区域表示平衡状态时的位置,而弹性体同一位置,不同颜色之间的距离就是位移u(f).在Γ1上,物体是被固定的,因此位移为零.在图2的右列,表示在T=1时刻弹性体的损伤分布,而初始的损伤场β0=1.

图3(a)(d)是基于无噪声的观测数据(ud,βd)的计算结果.蓝色实线表示真解f,而带星号红线是数值解.图3(a)中四幅子图分别表示：边界[0,L1]×{L2}上f的切方向(左上),边界[0,L1]×{L2}上f的法方向(右上),边界[0,L1]×{0}上f的切方向(左下),边界[0,L1]×{0}上f的法方向(右下).从图中可以看到,虽然在x=0.25m和x=1.75m的边界附近均有小幅波动,但反演结果还是很接近精确解.图3(d)中给出的是在细网格下的数值结果.

图3 基于不同噪声水平的观测数据(ud,βd)的结果,分别采用20×10和40×20的网格.蓝色实线表示真解f(47),带星号红线是数值解.六组图中,每组的第一行：边界[0,L1]×{L2}上;第二行：边界[0,L1]×{0}上;左列：f的切方向;右列：f的法方向.

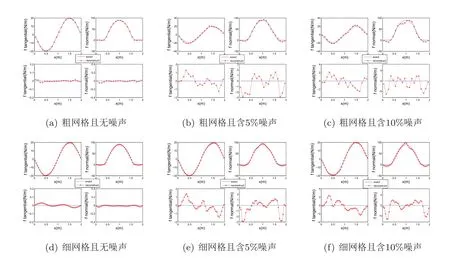
图4 基于不同噪声水平的观测数据(ud,βd)的结果.分别采用20×10和40×20的网格.蓝色实线表示真解f(48),带星号红线是数值解.六组图中,每组的每个子图第一行：边界[0,L1]×{L2}上;第二行：边界[0,L1]×{0}上;左列：f的切方向;右列：f的法方向.

图3(b)(e)给出的数值结果是基于含5%噪声的观测数据(ud,βd).与无噪声水平的数值结果相比,图3(b)(e)中的数值结果波动更明显.从图3(b)的左上图来看,最大的振幅位于x=1.7m附近,其次出现在x=0.4m附近,而从图3(b)的右上图和图2(误差情况与图5(a)相似)来看,可以发现f的法向分量在x=0.4m和x=1.7m是不连续的,而损伤变量的误差也是在x=0.1m和x=1.9m附近达到最大.此外,从细网格图3(e)中,振荡的幅度与粗网格相比并没明显的变化.图3(c)(f)给出了含10%噪声情况的数值结果,同样,用粗细网格作对比.显然,可观察到数值解的振荡更大,且最大和第二大振幅仍然出现在x=0.4m和x=1.65m附近.

因此,可以做出这样的结论：数值解的振荡,特别是第一和第二大的振幅处,可能是由f的不光滑和损伤变量的误差共同引起的.

表1 中,给出了不同噪声水平下的相对误差,相对误差的定义如(46).由表1,可以发现最大误差都是出现在最后一栏(10%噪声),这表明牵引力的重构与观测数据的噪声水平有直接关系.另外,在细网格下,误差会略微变小,这也说明可以适当的使用细网格来提高数值解的精度.

表1 重构例6.1的相对误差

例6.2.真解

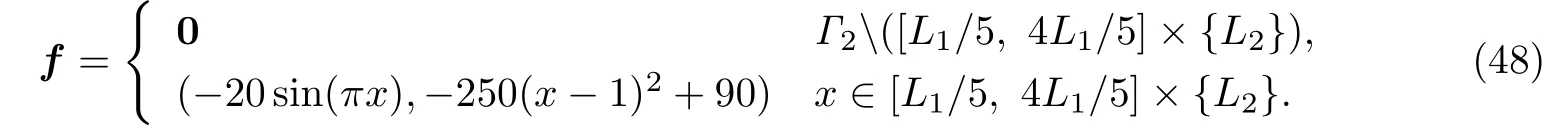
第二个例子,重构的牵引力f与例6.1相比,切向分量不为零(如(48)).图2的第一行给出了此实验弹性体的平衡状态和损伤场的分布情况.图4给出了在不同网格下,由不同噪声水平的观测数据得到的重构结果.通过观察发现,其最大和第二大振幅出现的位置同样是受f和损伤场重构误差(如图5(a))的影响.这与例6.1的情况一致.在表2中,也给出了不同噪声水平下的相对误差.

表2 重构例6.2的相对误差

例6.3.真解

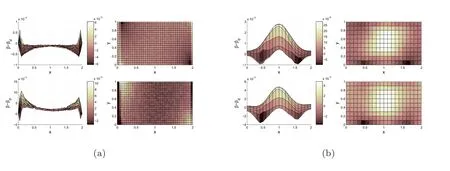
图5 损伤场的误差结果.所用网格为40×20,(a)图真解f是例6.2,(b)图真解f是例6.3.第一行：观测数据(ud,βd)无噪声.第二行：观测数据(ud,βd)有5%的噪声.左列：从y方向的投影图.右列：x-y平面上的投影图.

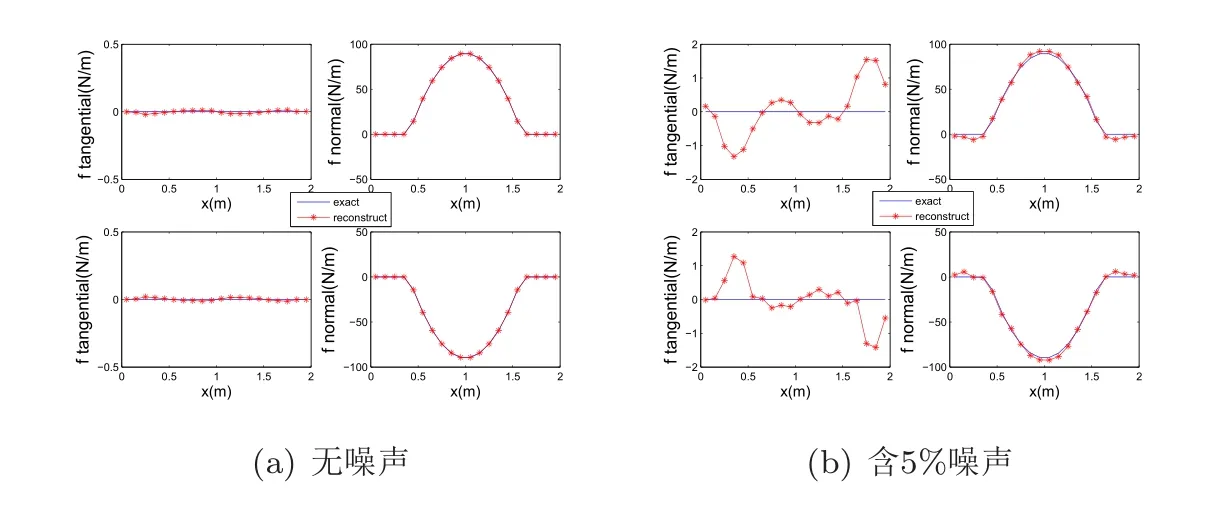
图6 基于不同噪声水平的观测数据(ud,βd)的结果,采用的网格是20×10.蓝色实线表示真解f(49),带星号红线是数值解fhα.两组图,每组图的第一行：边界[0,L1]×{L2}上;第二行：边界[0,L1]×{0}上;左列：f的切方向;右列：f的法方向.

最后,反演的牵引力如图1(a)展示的一样.即,在整个Γ边界上,牵引力的法向部分都不为零(49).在图2的第二行,给出了其最后时刻的平衡状态和损伤场的分布情况.在无噪声情况下,重构的结果非常好(如图6(a)).在5%噪声情况下(如图6(b)),最大振幅同样也是出现下损伤场误差最大(如图5(b))和f不光滑之间的区域.另外,与图3(b)的第二行图比较,这次的振荡幅度更小些.主要的原因可能是重构的损伤场更接近于精确值.

致谢 非常感谢各位审稿人给出的的宝贵意见和建议,使得论文增色不少.

[1] Tichonov A,Arsenin V.Solution of ill-Posed Problems[M].New York：John Wiley,1977.

[2] Chiou W,Chen C,Lu Wensheng.The inverse numerical solutions of the nonlinear heat transfer problem in electrical discharge machining[J].Numer Heat Trans,Part A：Appl,2011,59(4)：247-266.

[3] Kaipio J,Somersalo E.Statistical and Computational Inverse Problems[M].New York：Springer,2005.

[4] Samarskii A A,Vabishchevich P N.Numerical Methods for Solving Inverse Problems of Mathematical Physics[M].Berlin：Walter de Gruyter,2007.

[5] Maniatty A,Zabaras N,Stelson K.Finite element analysis of some inverse elasticity problems[J].J Eng Mech Diu ASCE,1989,115：1302-1316.

[6] Zabaras N,Morellas V,Schnur D.A spatially regularized solution of inverse elasticity problems using the boundary element method[J].Commun Appl Numer Methods,1989,5：547-553.

[7] Yeih W,Koya T,Mura T.An inverse problem in elasticity with partially overprescribed boundary conditions,1.Theoretical approach[J].J Appl Mech-T ASME,1993,60：595-600.

[8] Martin T,Halderman J,Dulikravich G.An inverse method for fi nding unknown surface traction and deformations in elastostatics[J].Comput Struct,1995,56：825-835.

[9] Marin L,Elliott L,Ingham D B,et al.Boundary element method for the Cauchy problem in linear elasticity[J].Engineer Anal Boundary Elements,2001,25(9)：783-793.

[10]Gao Zhanjun.Damage evaluation from surface displacement data[D].Northwestern Univ,1989.

[11]Kogut Peter I,Leugering Günter.On existence of optimal solutions to boundary control problem for an elastic body with quasistatic evolution of damage[J].Solid Mech Appl,2014,211：265-286.

[12]Sofonea M,Matei A.Mathematical Models in Contact Mechanics[M].Cambridge：Cambridge University Press,2012.

[13]Frémond M,Nedjar B.Damage,gradient of damage and principle of virtual work[J].Int J Solids Struct,1996,33：1083–1103.

[14]Kuttler K L,Shillor M.Quasistatic evolution of damage in an elastic body[J].Nonlinear Anal：Real World Appl,2006,7：674-699.

[15]Murakami S.Continuum Damage Mechanics：A Continuum Mechanics Approach to the Analysis of Damage and Fracture[M].Amsterdam：Springer,2012.

[16]Zhang Wohua,Cai Yuanqiang.Continuum Damage Mechanics and Numerical Applications[M].Berlin：Springer-Verlag,2010.

[17]Campo M,Fern´andez J R,Kuttler K L,et al.Quasistatic evolution of damage in an elastic body：numerical analysis and computational experiments[J].Appl Numer Math.2007,57：975-988.

[18]Atkinson K,Han Weimin.Theoretical Numerical Analysis：A Functional Analysis Framework 3rd edn[M].New York：Springer,2009.

Numerical analysis of inverse elastic problem with damage

ZHENG Cong,CHENG Xiao-liang,LIANG Ke-wei
(School of Math.Sci.,Zhejiang Univ.,HangZhou 310027,China)

The quasistatic elastic problem is formulated as an elliptic system for the displacements coupled with a parabolic equation for the damage fi eld.The corresponding inverse problem is reformulated as an optimal control problem to fi nd a stable traction,by a given observation data.Firstly,a convex functional is constructed with Tikhonov regularization,and a stable approximation of surface traction is obtained by minimizing it.Then a fi nite element discretization of the inverse elastic problem is analyzed.Moreover,the error estimation of the numerical solutions is deduced.At last,a numerical algorithm is detailed and three examples illustrate the efficiency of the algorithm.

variational inequality; fi nite element method;error estimates;numerical simulations

65M15;65M32;74S05

O241.82

A

：1000-4424(2016)04-0476-15

2016-01-15

2016-04-16

国家自然科学基金(11271258;11471253;11571311)