非线性对流扩散方程的三层隐-显hp-局部间断Galerkin有限元方法

由同顺

(南开大学数学科学学院,天津300071)

非线性对流扩散方程的三层隐-显hp-局部间断Galerkin有限元方法

由同顺

(南开大学数学科学学院,天津300071)

使用Arnold等人提出的求解椭圆方程的间断有限元的一般框架及新的处理非线性对流项的方法,得到了非线性对流扩散方程的三层隐-显hp-LDG方法的误差估计.对Burgers方程进行了数值计算,计算结果验证了文中得到的理论结果.

对流占优扩散方程;三层隐-显hp-LDG方法;提升算子

§1 引 言

间断Galerkin有限元(DG)方法是有限体积方法的高阶推广,它本身具有局部守恒性,稳定性及高精度等特点,近年来一直受到人们的广泛重视并在流体力学等领域有许多应用.关于DG方法的综述可参见文献[1-5].

文[4]对于对流扩散方程,提出了局部间断Galerkin有限元(LDG)方法并对具有常系数线性问题给出了误差分析.文[6]讨论了非线性对流扩散方程的hp-LDG方法,得到了空间半离散hp-LDG格式的误差估计.为了避免使用小的时间步长,文[7]讨论了非线性对流扩散方程的一阶隐-显hp-局部间断Galerkin有限元方法,得到一阶全离散隐-显hp-LDG的误差估计.为了提高时间精度,本文采用二阶精度离散时间变量,对于对流项采用二阶显格式而对于扩散项采用隐格式离散且对于非线性项采用二阶外推技巧,提出了求解非线性对流扩散方程的二阶隐-显hp-局部间断Galerkin有限元方法并在[1,8,6]的框架下,使用不同于文[4]的方法,采用文[1,8]对于椭圆方程提出的提升算子方法以及使用不同于[9]处理对流项的方法,得到了非线性对流扩散方程的全离散二阶隐-显hp-LDG方法的误差估计.本文给出的数值算例验证了理论结果.

本文讨论的模型问题为

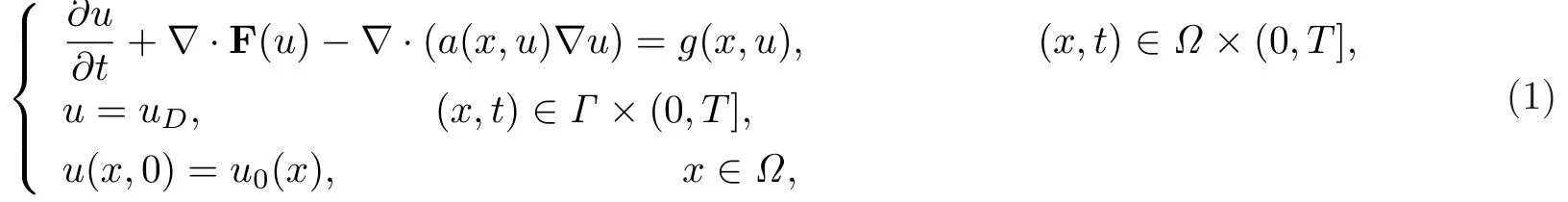
其中Ω是R2中的多角形区域,F(u)=(f1(u),f2(u))T.假设系数及右端项满足下列条件H1：

1.对(x,p)∈ Ω ×R,存在正常数a∗及 a∗,使得a∗≤ a(x,p)≤ a∗,fs∈ C1(R)(s=1,2);

2.系数a(x,u),g(x,u)关于u是一致Lipschitz连续的.

设Th={K}是Ω的正则三角形或四边形剖分,用hK表示单元K的直径,用εI表示Th全体非空内边界的集合,即对任一e∈εI,存在Th中的两个相邻单元K+及K-,使得e=∂K+∩∂K-;用εD表示Ω的全体非空边界边的集合,即对任一e∈εD,存在Th中的一个边界单元K,使得e=∂K∩∂Ω;记ε=εI∪εD.用pK≥1表示单元K ∈Th中的多项式的次数.记p ={pK}K∈Th.现定义hp-有限元空间为

§2 三层隐-显hp-LDG格式

为构造LDG格式,引入辅助变量σ=a(x,u)s和s=∇u,则对流-扩散问题(1)可改写为

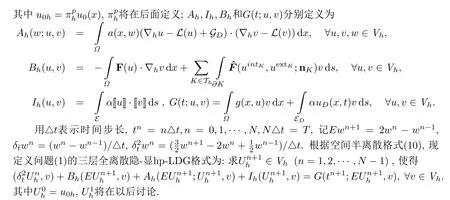
§3 误差估计

设问题(1)的解u∈H2(Ω),则

类似于[10]中的引理4.11及[8]中的引理3.2的证明,可知

由投影算子ΠQh及提升算子L的定义,引理3.3和引理3.1,可知

当△t足够小时,由离散的Grownwall不等式,可得

§4 数值例子

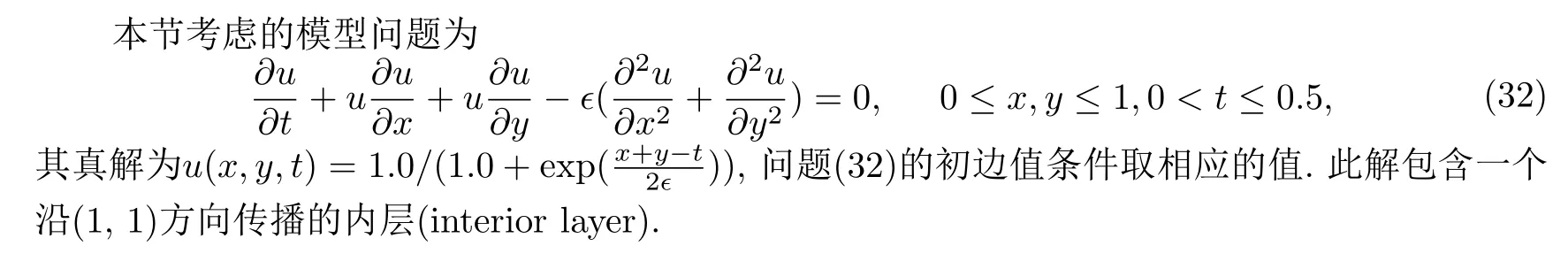
本文使用二阶隐-显LDG格式分别对ϵ=0.1及ϵ=0√.02的Burgers方程进行了数值计算.在计算中,对流数值流选为Lax-Friedrichs流,其中M=+1.0E-10.另外,罚参数选为α=1/h及β=0.5n(n为单元K的单位外法向量),等分正方形区域Ω =[0,1]×[0,1]为N2个小正方形,然后再从左上到右下连接小正方形的对角线,形成两个三角形,其三角形直边长为h=1.0/N.为了计算关于空间步长h的误差阶,时间步长取为△t=0.0001,选取空间步长为h=1.0/N,N=2,4,8,16,32,64.另外,为了计算关于时间步长△t的误差阶,选取空间步长为h=1.0/128,时间步长取为△t=0.1/M,M=2,4,8,16,32,64.在表中,L2(H1)-范数为关于初始步的计算,可以使用二阶显式RK方法或CN方法对半离散方程(10)的时间变量t进行离散.在本例计算中,初始两步的值取为真解的相应值.从表中可以看到,计算结果验证了理论结果(在表1中,p=3,N=64时,‖e‖L2(ϵ=0.1)的误差阶的降低是由于时间方面的误差(△t)2=1.0E-08大造成的).

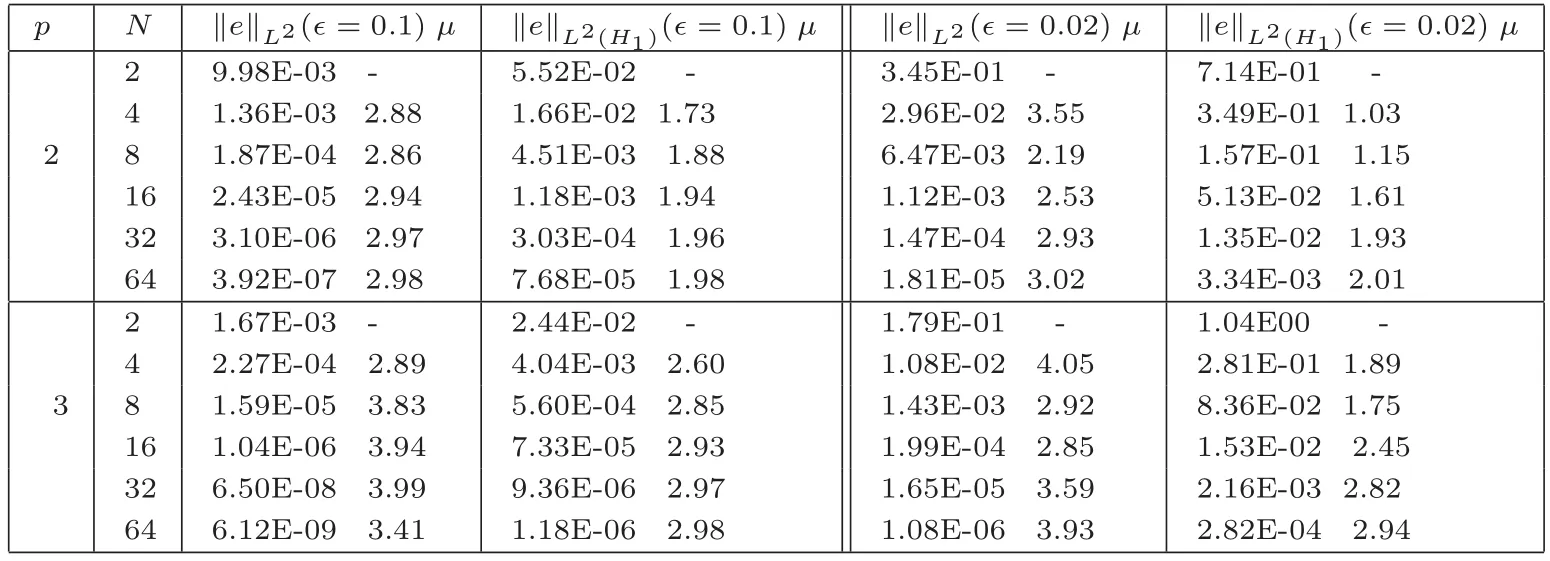
表1 关于h的误差阶µ,t=0.5,β=0.5n, α=1.0/h

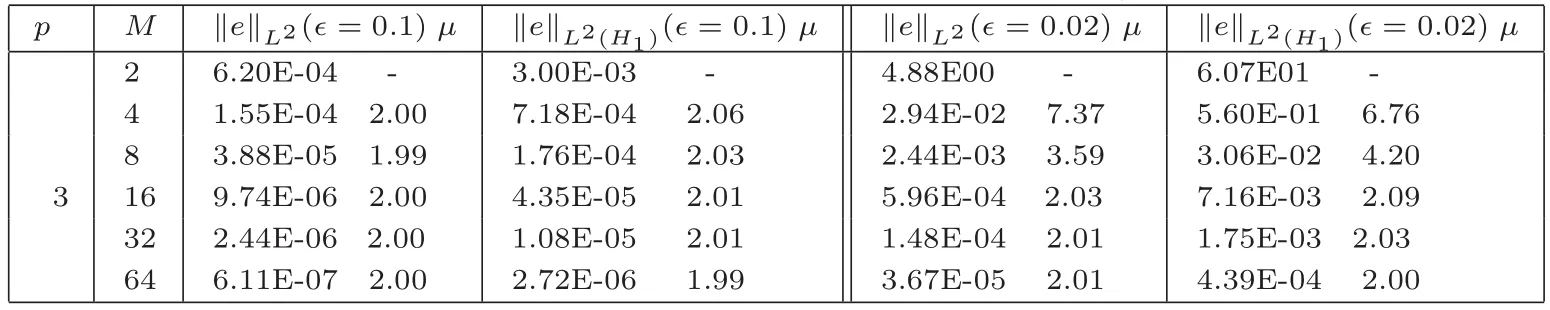
表2 关于△t的误差阶µ,t=0.5,β=0.5n, α=1.0/h

[1] Arnold D N,Brezzi F,Cockburn B,et al.Uni fi ed analysis of discontinuous Galerkin methods for elliptic problems[J].SIAM J Numer Anal,2001,39：1749-1779.

[2] Cockburn B,Karniadakis G,Shu C W.eds,Discontinuous Galerkin Methods.Theroy,Computation and Applications[A],Lecture Notes in Computational Science and Engineering[C].Vol.11,Berlin：Springer Verlag,2000.

[3] Cockburn B,Shu C W.Runge-Kutta discontinuous Galerkin methods for convectiondominated problem[J].J Sci Comput,2001,16：173-261.

[4] Cockburn B,Shu C W.The local discontinuous Galerkin method for time-dependent convection-di ff usion systerms[J].SIAM J Numer Anal,1998,35：2440-2463.

[5] Castillo P,et al.An a priori error analysis of the local discontinuous Galerkin method for elliptic problems[J].SIAM J Numer Anal,2000,38：1676-1706.

[6] You Tongshun.The hp-local discontinuous Galerkin fi nite element method for nonlinear convection di ff usion problems[J].工程数学学报,2012,29：894-906.

[7] You Tongshun.非线性对流扩散方程的隐-显hp-局部间断Galerkin有限元方法[J].高校应用数学学报,2013,28：447-456.

[8] Perugia I,Sch¨otzau D.An hp-analysis of the local discontinuous Galerkin method for di ff usion problems[J].J Sci Comput,2002,17：561-571.

[9] Dolejsi V,Feistauer M,Sobotikova V.Analysis of the discontinuous Galerkin methods for nonlinear convection-dominated problems[J].Comput Methods Appl Mech Eng,2005,194：2709-2733.

[10]Perugia I,Sch¨otzau D.The hp-local discontinuous Galerkin method for low-frequency timeharmonic Maxwell equations[J].Math Comp,2003,72：1179-1214.

[11]Cockburn B,Shu C W.The Runge-Kutta discontinuous Galerkin fi nite element method for conservation laws V：Multidimensional systems[J].J Comput Phys,1998,141：199-224.

[12]Brezzi F,Manzini G,Marini D,et al.Discontinuous Galerkin approximations for elliptic problems[J].Numer Methods for Partial Di ff erential Equations,2000,16：365-378.

[13]Babuˇska I,Suri M.The hp-version of the fi nite element method with quasiuniform meshes[J].RAIRO Anal Numér,1987,21：199-238.

[14]Houston P,Schwab C,Süli E.Discontinuous hp- fi nite element methods for advectiondi ff usion-reaction problems[J].SIAM J Numer Anal,2002,39：2133-2163.

[15]Ewing R E,Russell T F.Multistep Galerkin Method along characteristics for convectdi ff usion problems[A],Advances in Computer Methods for Partial Di ff erential Equations[C].Vichnevetsky R,Stepleman R S,eds.,IMACS,1981,28-36.

The three-step implicit-explicit hp-local discontinuous Galerkin fi nite element method for nonlinear convection di ff usion problems

YOU Tong-shun
(College of Mathematics,Nankai University,Tianjin 300071,China)

By using the general framework introduced in Arnod et al.and the new method dealting with the nonlinear convection term,the error estimates of three-step implicit-explicit hp-LDG method for nonlinear convection di ff usion problems are obtained.The numerical example for the nonlinear Burgers equation is presented in the paper.The numerical results verify the theoretical results obtained in this paper.

convection di ff usion equation;three-step implicit-explicit hp-LDG method;lifting operator method

65N12;65N15;65N30

O241.8

A

：1000-4424(2016)04-0491-10

2016-03-11

2016-06-28