渗透数学思想方法在高中数学函数教学中的应用
高兴亮
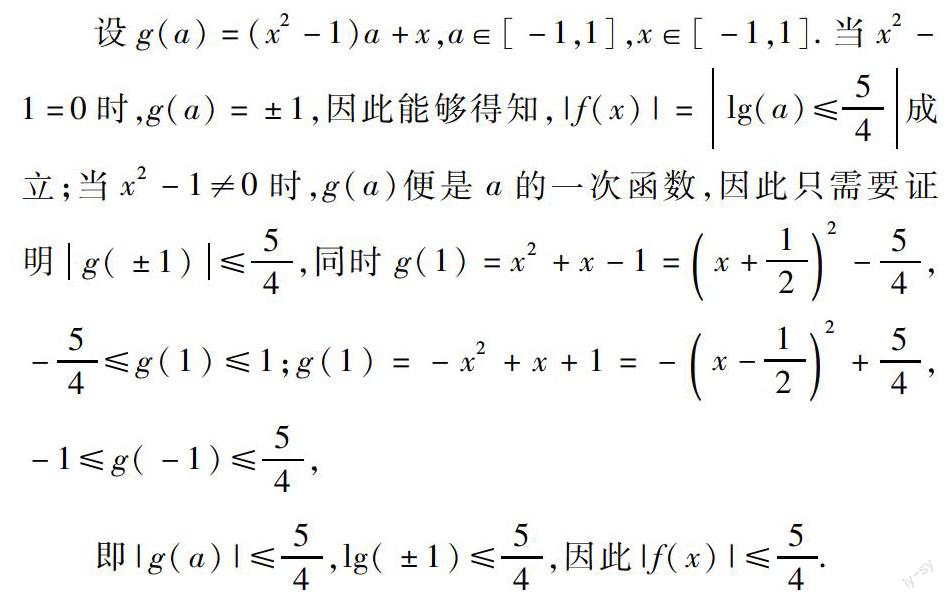
【摘要】数学思想是了解数学知识和方法的基本条件,也是对数学知识结构整体的认识.数学思想方法是解决数学问题的常见方式.在高中数学函数教学过程中,渗透数学思想能够引导学生形成合理的认知结构,并且能够运用相关数学思想将知识转化为解决问题的能力.本文作者根据多年教学经验,对高中数学函数的教学提出了集中常见的数学思想,仅供参考.
【关键词】数学思想方法;高中数学;函数教学
函数是高中数学的重点教学内容,也是学生重点掌握知识,函数知识具有独特的整体性与逻辑性.再加上函数知识在生活中常常遇到,函数知识能够帮助学生解决生活中遇到的问题,从而有效显示数学知识的价值.因此,作为数学重要知识的函数,在教学过程中教师应该注重培养学生数学思想,有利于学生运用数学知识有效解决函数问题.
一、渗透举一反三的数学思想方法
在学习高中数学的时候,有效的解题方法是培养学生数学思想方法的基础,因此在学习高中函数的过程中就可以采用举一反三的方式培养学生解题的思路,针对一些典型的数学例题进行重复练习,增强学生对这类型题目理解和掌握程度!
在高中数学学习过程中,科学合理的解题方法是培养学生数学思想的基础,所以在高中函数教学过程中可以渗透举一反三的数学思想,重复练习一些典型的数学立体,提高学生对这一类型函数题目的理解与掌握.例如,在讲解“求y=x2+4x-2同横坐标存在几个交叉点”时,老师讲解完这一类型题目的知识点后,便基于这一知识点设计一系列有关问题,例如,“求y=x2+4x-2与x=4的交点”和“求y=x2+4x-2与横坐标存在几个交点”等各种问题,要求学生根据所学知识进行解答,从而培养学生举一反三的数学思想.
二、渗透化归数学思想方法
化归数学思想是指把未知的问题转变为已有知识范围内能够解决问题的一种数学思想方法,这一思想方法能够把陌生、抽象、复杂的问题转变为熟悉、具体、简单的问题.化归思想方法是高中数学函数教学和学习的主要方法,其应用于整个函数学习过程中,引导学生合理转化问题,剖析出已知条件同结题目标之间的关联.渗透化归数学思想,有助于培养学生抽象思维、创造性思维、发散思维与想象思维,从而提高学生分析与解决问题的能力.
例如,设|a|≤1,函数f(x)=ax2+x-a,求:当x≤1时,|f(x)|≤54.这便是二元函数求最小值的题目,应该采用化归思想方法把这道题转化为一元函数求最值.如果把a看作主元,问题中函数当作a的一次函数,那么便能够将题目转化为:一次函数g(a)=(x2-1)a+x的最小值不得≥1,求其范围,解题过程如下:
设g(a)=(x2-1)a+x,a∈[-1,1],x∈[-1,1].当x2-1=0时,g(a)=±1,因此能够得知,|f(x)|=lg(a)≤54成立;当x2-1≠0时,g(a)便是a的一次函数,因此只需要证明g(±1)≤54,同时g(1)=x2+x-1=x+1[]22-54,-54≤g(1)≤1;g(1)=-x2+x+1=-x-1[]22+54,-1≤g(-1)≤54,即|g(a)|≤54,lg(±1)≤54,因此|f(x)|≤54.
三、渗透数形结合数学思想方法
数形结合是数学中常见的思想方法之一.其能够采用直观的方法将抽象的数量关系在空间或平面上表现出来,能够巧妙地将抽象思维和形象思维集合起来处理各种数学问题的解题方式.伟大数学家华罗庚曾讲到“数缺形时少直观,形少数时难入微,数形结合百般好,割裂分家万事休.”如果只是凭借数量关系难以着手解决问题,如果把数量关系转变为相对应的图形,同时利用其图形规律性来进行确定,借助直观易懂的图形来秒回出數量之间的关系,能够将复杂难懂的函数问题转变为简单、容易的图形问题进行解决.因此,对于一些抽象的函数题,教师在讲解过程中应该引导学生采用数形结合的思想方法,轻松解答出答案.例如,求y=(cosθ-cosα+3)2+(sinθ-sinα-2)2的最值(θ,α∈R),能够利用距离函数模型来解答该题.
四、渗透分类讨论数学思想方法
分类讨论数学思想是一种“化整为零为整”的方法.在解决和分析数学问题时,研究对象难以进行统一研究的情况下便可以按照数学对象的本质属性的不同之处,把问题对象划分为不同的类别,然后再一一进行研究讨论,从而最终有效解决整个数学问题.
在高中数学函数教学过程中,常常会进行函数相关性质、定理、公式等相关分类讨论,这些问题中均存在各种变量或需要讨论的参数,这便要求我们进行分类讨论.在教学过程中有计划、有目的地渗透分类思想,在潜移默化中增强学生数学思维能力.
数学思想实质上是深入理解和认识数学概念、理论相关知识,也是全面总结归纳数学知识的一种思想.在教学过程中,潜移默化中向学生渗透数学解题方法,指导学生有效解决各种数学问题.数学思想方法的渗透不仅仅是一种教学方法,更是提高学生数学综合能力的一种有效策略,值得在高中数学教学中广泛应用.

