基于齿面摩擦的人字齿轮副动力学特性分析

陆凤霞， 王浩飞， 朱如鹏， 鲍和云， 姜慧卉

(南京航空航天大学 机电学院，江苏 南京　210016)

基于齿面摩擦的人字齿轮副动力学特性分析

陆凤霞， 王浩飞， 朱如鹏， 鲍和云， 姜慧卉

(南京航空航天大学 机电学院，江苏 南京210016)

摘要：建立了考虑齿面摩擦、时变啮合刚度、齿侧间隙和综合传递误差的16自由度人字齿轮副三维空间弯曲-扭转-轴向耦合的非线性动力学模型，应用牛顿第二运动定律，建立系统的振动微分方程。根据人字齿轮副的啮合特性，通过数值积分方法分析了轮齿的啮合力,时变摩擦力和摩擦力矩，并采用基于弹流润滑理论(EHL)的摩擦因数计算模型计算了齿面摩擦因数。为了分析齿面摩擦对人字齿轮副周期振动及分岔特性的影响规律，比较了有无考虑齿面摩擦时系统的周期振动时域响应、振动位移分岔图及最大lyapunov指数变化图。结果表明，齿面摩擦导致齿轮副垂直于啮合平面方向的振动位移加剧，且减弱了齿轮副沿啮合线方向的振动。同时，齿面摩擦的存在使得系统提前进入混沌，且抑制了系统的混沌运动。文章的研究成果有助于进一步认识齿面摩擦对人字齿轮传动周期振动及非线性振动特性的影响，为人字齿轮传动设计提供技术依据。

关键词：齿面摩擦；人字齿轮；混沌；分岔

人字齿轮传动具有传动效率高、结构紧凑、承载能力大和轴承轴向负载低等优点，被广泛应用于舰船等大功率机械传动系统中。近年来吸引了国内外大量学者对其动力学特性开展研究。王成等[1]分析了人字齿轮副的振动特性。Yang等[2]分析了人字齿轮副均载特性以及非线性振动响应。郭家舜等[3]建立了单级人字齿轮副的弯-扭-轴耦合动力学模型，对系统进行动力学分析。

齿轮副工作过程中，摩擦力的大小、方向均发生周期性的变化，形成一种非谐波型的内激励，这是齿轮传动系统振动和噪声的重要激励之一。Velex等[4]建立了考虑齿面摩擦的直齿轮和斜齿轮传动的动力学模型。He等[5]建立了含摩擦力的12自由度斜齿传动系统的分析模型，研究分析了摩擦力对系统动力学的影响。Liu等[6]建立了含摩擦的人字齿轮副模型，分析了误差、摩擦因数对人字齿轮副振动特性的影响，但未能研究齿面摩擦对齿轮副非线性振动特性的影响。朱恩涌等[7]建立了含摩擦力的2K-H型行星齿轮系非线性动力学模型，分析了摩擦力对系统动力学特性的影响。

在人字齿轮副动力学特性分析中，同时考虑齿面摩擦、误差、时变啮合刚度、齿侧间隙影响的文献目前国内外还未见报道。本文在上述研究基础上，建立了人字齿轮副弯曲-扭转-轴向耦合的非线性动力学模型。基于人字齿轮副的啮合特性计算了人字齿轮副的啮合力、摩擦力与摩擦力矩。采用基于弹流润滑理论(EHL)的摩擦因数计算模型，研究分析了齿面摩擦对人字齿轮副振动及分岔特性的影响。研究成果有助于进一步认识摩擦激励对人字齿轮副动力学特性的影响，为人字齿轮副的设计分析提供参考。

1人字齿轮副动力学模型

图1为人字齿轮副动力学模型。以垂直于啮合平面方向为x方向，齿轮的轴向为z方向建立坐标系。人字齿轮传动一般采用小轮浮动的方式，每个齿轮均具有x，y和z方向的平移以及绕z轴扭转的四个自由度。

图1　人字齿轮副动力学模型Fig.1 The dynamics model of double helical gears

图1中，T1和T2分别为输入和输出扭矩；km1，km2，cm1和cm2分别为齿轮副1，2的啮合刚度和啮合阻尼；kix，kiy，kiz，cix，ciy和ciz分别为齿轮i沿x，y和z方向的支撑刚度以及支撑阻尼(i=1，2，3，4)；k13x，k13y，k13z，J1，k24x，k24y，k24z和J2分别为两个齿轮轴的x和y方向弯曲刚度和轴向拉伸刚度以及扭转刚度；c13x，c13y，c13z，ct1，c24x，c24y，c24z和ct2分别为两个齿轮轴x，y，z方向以及扭转方向的阻尼。

1.1人字齿轮副啮合特性分析

图2为人字齿轮副啮合过程的示意图。其中，图2(b)中两条虚线之间的区域为接触区域。

图2　人字齿轮副的啮合过程Fig.2 Illustration of meshing process of double helical gears

图2(a)中，N1和N2分别为理论啮合线的起点和终点；A和B分别为实际啮合线的起点和终点；P为节点；C为啮合点；其余参数的物理意义文中均有详述。

定义第i对接触轮齿从进入啮合区域开始经过时间t后移动的距离为：

si=ω1rb1[mod(t,Tm)+(i-1)Tm]

(1)

式中，ω1和rb1分别为齿轮1的转速以及基圆半径；Tm为啮合周期；mod()为取余函数。

假设两齿轮的接触线在前端面B点处的曲率半径分别为Rt1和Rt2，则在接触线上距B点l处的一点K，两齿轮在该点的曲率半径RtK1和RtK2分别为：

(2)

式中，Rt1和Rt2可以通过下式计算得到：

(3)

根据人字齿轮的几何特性可知，在K点处齿轮1和齿轮2上的法向曲率半径分别为：

(4)

齿轮1和齿轮2在K点处接触齿面的综合曲率半径、沿齿面方向的滑动速度分别为：

(5)

式中，ωi，rbi和αtKi分别为齿轮i的角速度和基圆半径以及K点的端面压力角(i=1，2)。其中，αtKi可通过式(6)计算得到：

(6)

K点处的齿面相对滑动速度、相对滚动速度、滑滚比以及卷吸速度分别为：

(7)

1.2齿轮副动态啮合力

人字齿轮副可看作由两对旋向相反的斜齿轮副组成，其啮合过程与斜齿轮相似，即均是逐渐进入啮合再逐渐退出啮合。本文分别计算人字齿轮副左、右两端斜齿轮副的啮合力、摩擦力及摩擦力矩。

一对斜齿轮副中，第i对接触轮齿间沿啮合线方向的相对变形为：

δi=(y2-y1+rb1θ1-rb2θ2)cosβb+

(z1-z2)sinβb-ei

(8)

式中，ei为第i个接触齿对间的齿形误差。本文中认为误差沿接触线均匀分布[16]。

第i对接触轮齿间的弹性啮合力可通过下式计算得到：

Fi=∫lkif(δi)dl

(9)

式中，l为第i对接触轮齿之间的接触线长度；ki为轮齿单位接触线上的刚度；f(δ)代表齿轮副中齿侧间隙的分段计算函数。

当εα>εβ时，

(10)

式中，a1=si/sinβb；a2=b/cosβb；a3=b/cosβb-(si-lm)/sinβb；εγ，εα和εβ分别为齿轮副的重合度、端面重合度及轴向重合度，且εγ=εα+εβ；βb为基圆螺旋角；Pbt为齿轮的端面基节；N为斜齿轮副中同时参与啮合的轮齿对数的最大值，N=ceil(εγ)，ceil(x)为大于等于x的最小整数。lm为齿轮副实际啮合线的长度：

(11)

式中，rai，rbi和ri分别为齿轮i的齿顶圆半径、基圆半径和分度圆半径(i=1，2)；αt为齿轮副的端面压力角。

当εα<εβ时，

(12)

式中，a1=si/sinβb；a2=lm/sinβb；a3=b/cosβb-(si-lm)/sinβb

一对斜齿轮副的弹性啮合力为：

(13)

1.3齿面的时变摩擦力和摩擦力矩

齿面摩擦因数主要受轮齿几何形状、表面硬度、接触压力和齿面相对滑动速度等因数的影响[9]。实验数据表明基于弹流润滑理论计算得到的摩擦因数[11]与实际测得的摩擦因数更为接近，本文即采用该摩擦因数计算模型。

基于弹流润滑理论的摩擦因数计算模型为：

(14)

式中，f(SR,Ph,v0,s)可由下式获得，即：

(15)

式中，SR为两个接触齿面的滑滚比；ν0为润滑油的动力黏度，单位为cps；Ve为齿轮接触点处的卷吸速度；S为表面粗糙度的均方根值，单位为μm；b1,b2,…,b9的值参照文献[11]，依次在表1中给出。

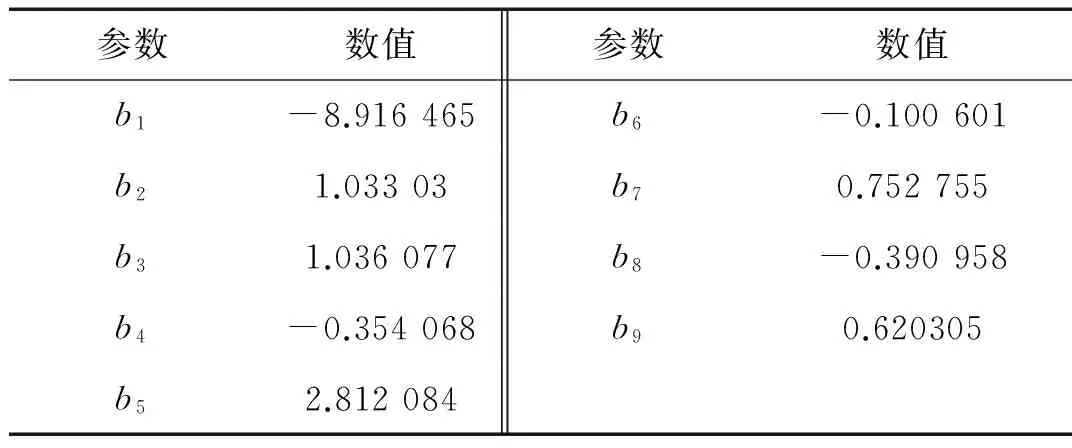
表1　EHL摩擦因数计算模型中参数赋值

SR的计算公式如下：

(16)

式中，Vs和Vr分别为两个接触齿面的相对滑动速度和相对滚动速度，单位为m/s。

最大赫兹接触应力Ph可通过式(17)计算得到:

(17)

式中，W′为轮齿的单位法向载荷；E′为等效弹性模量；R为接触点处的综合曲率半径，单位为m。

通过该摩擦因数计算模型，得到摩擦因数随滑滚比的变化曲线见图3所示。

图3　摩擦因数随滑滚比变化曲线Fig.3 The friction curve under the EHL model

第i个接触齿对间的摩擦力和摩擦力矩可以通过下式计算得到:

(18)

式中，fi，Tf1i和Tf2i分别为第i对接触轮齿间的摩擦力和摩擦力对齿轮1的力矩以及摩擦力对齿轮2的力矩。

由斜齿轮啮合特性可知，节线两侧接触线上的摩擦力方向相反，接触线被节线分为两个部分。分别对两部分接触线上的摩擦力和摩擦力矩进行积分即可得到整条接触线上的摩擦力和摩擦力矩，如下式：

(19)

式中，a1和a2分别为第i条接触线位于节线两侧部分的长度(如图4所示)。

图4　啮合区域的划分Fig.4 Division of the meshing area

为便于对式(19)进行数值积分，根据接触线在啮合区域的位置，将接触区域划分为六个部分。当εα>εβ时，接触线从进入啮合区域到完全退出啮合的过程如图4(a)所示：

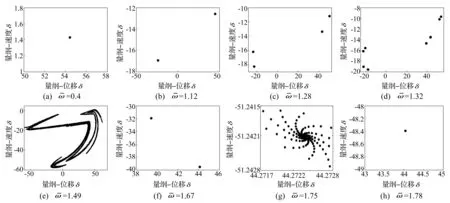
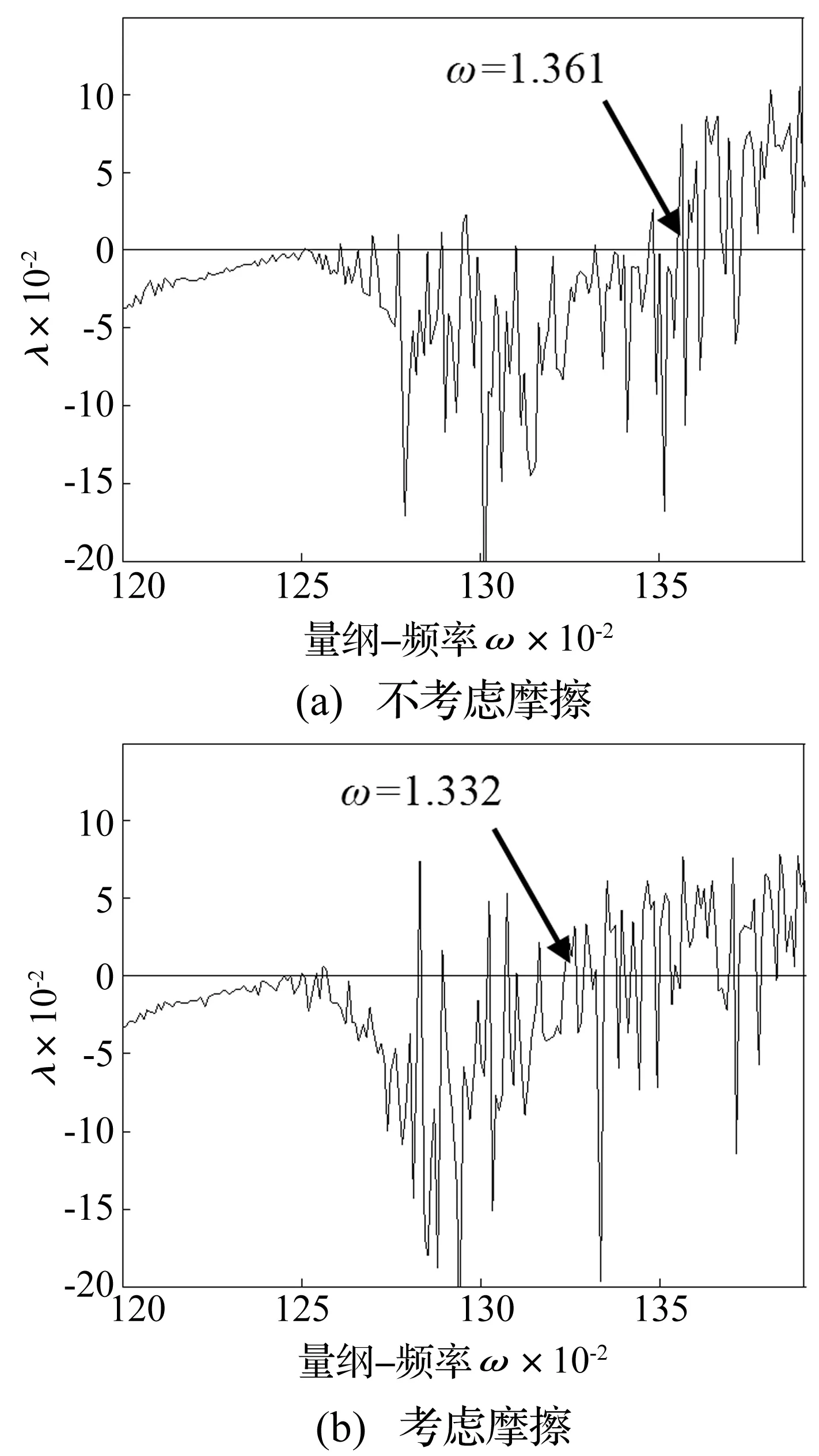
区域1，即0≤si

a1=si/sinβb，a2=0

区域2，即l2≤si<εβPbt时有：

a1=l2/sinβb，a2=(si-l2)/sinβb

区域3，即εβPbt≤si<εαPbt时有：

a1=(l2+εβPbt-si)/sinβb，a2=(si-l2)/sinβb

区域4，即εαPbt≤si<εβPbt+l2时有：

a1=(l2+εβPbt-si)/sinβb，a2=l1/sinβb

区域5，即εβPbt+l2≤si<εβPbt+lm时有：

a1=0，a2=(lm-si+εβPbt)/sinβb

区域6，即εβPbt+lm≤si

a1=0，a2=0

式中，a1和a2分别为位于节线左侧和右侧的接触线长度；l1和l2分别为节线到啮合开始边界和终止边界的距离，计算公式如下：

(20)

式中，rai，rbi和ri分别为齿轮i的齿顶圆半径、基圆半径和分度圆半径(i=1，2)。

当εα<εβ时，接触线从进入啮合区域到完全退出啮合的过程如图4(b)所示。

区域1，即0≤si

a1=si/sinβb，a2=0

。

区域2，即l2≤si<εαPbt时有：

a1=l2/sinβb，a2=(si-l2)/sinβb

区域3，即εαPbt≤si<εβPbt时有：

a1=l2/sinβb，a2=l1/sinβb

区域4，即εβPbt≤si<εβPbt+l2时有：

a1=(l2+εβPbt-si)/sinβb，a2=l1/sinβb

区域5，即εβPbt+l2≤si<εβPbt+lm时有：

a1=0，a2=(lm-si+εβPbt)/sinβb

区域6，即εβPbt+lm≤si

a1=0，a2=0

一对斜齿轮副的啮合力、摩擦力和摩擦力矩可以由下式计算得到：

(21)

1.4人字齿轮副动力学微分方程

基于上述分析，利用牛顿第二运动定律得到16个自由度的人字齿轮副弯曲-扭转-轴向耦合的弹性动力学运动微分方程，即：

(22)

式中，xi，yi，zi和θi分别为齿轮i沿x，y和z方向的振动位移以及绕z轴的扭转振动位移；mi，Ii和rbi分别为齿轮i的质量、转动惯量和基圆半径；Tfi分别为摩擦力对齿轮i的力矩(i=1，2，3，4)；F1和F2分别为齿轮副1和齿轮副2上的啮合力；f1和f2分别为齿轮副1和齿轮副2上的摩擦力；β1和β2分别为齿轮副1和齿轮副2的螺旋角。

1.5系统量纲一方程

由于齿侧间隙的存在，使得系统约束不完整，式(22)为半正定系统[17]，存在着刚体位移以及不定解。为消除刚体位移，在保持系统拓补解结构不变前提下，利用同胚映射，使系统方程数目减少从而实现降维。引入相对坐标：

(23)

式中，δy1和δy2分别代表齿轮副1和齿轮副2啮合平面内平移-扭转耦合振动位移；δ13和δ24分别代表齿轮1和齿轮3之间及齿轮2和齿轮4之间的相对扭转位移。

由式(23)可知：

δ24=δ13+δy2-δy1-y1+y2+y3-y4

(24)

(25)

将经过量纲一化和消除刚体位移处理的系统动力学微分方程整理为矩阵形式：

(26)

式中，X，M，K，C和F分别为位移向量、质量矩阵、刚度矩阵、阻尼矩阵及激励力向量；其中：

(27)

由于阻尼值较难获取，本文采用瑞利阻尼形式[8]，阻尼矩阵由刚度矩阵及质量矩阵表示，即：

C=αM+βK

(28)

式中，α和β分别为质量矩阵系数和刚度矩阵系数，可由文献[8]中计算方法得到。

2人字齿轮副动力学分析

为简化计算，假设齿轮单位接触线上刚度ki为定值，可查阅齿轮设计手册得到该值。采用变步长4阶龙格库塔(Runge-Kutta)法求解动力学方程，算例参数如表2所示。

计算初值全部选取为0，考虑初始值的影响，将开始数百个周期内的响应略去，得到系统的时域响应。

表2　算例参数

2.1摩擦力对人字齿轮振动位移的影响

考虑到人字齿轮副中各齿轮振动特性的一致性，仅以齿轮1为研究对象。

有无考虑齿面摩擦两种情形下，齿轮1沿x，y，z方向的平移振动位移及齿轮1和2之间弯扭耦合振动位移δy的时域、频域响应如图5～图9所示。

从图5可看出，由于齿面摩擦力的存在，齿轮的x方向平移振动位移显著增加。由图5的频域图还可以看出，在前5阶频段内，摩擦力对该方向上齿轮的平移振动均有较显著的影响。因此，齿面摩擦将会导致齿轮垂直于啮合线方向的振动显著加剧。

图6表明，由于齿面摩擦的存在，齿轮1沿y方向的平移振动位移小于不存在齿面摩擦时该方向的振动位移，这表明齿面摩擦抑制了轮齿啮合力的波动，减小了啮合线方向的振动。这与文献[6]的结论一致，从而验证了本文模型的正确性。由图6的频域图还可以看出，摩擦力对啮合线方向的影响主要是在前两阶频段内，高阶频段内齿面摩擦对系统该方向的振动影响较弱。

图5　齿轮1的x方向平移振动位移时域谱及频域谱Fig.5 The time-domain spectrum and the frequency spectrum of the translation displacement in x direction of gear 1

图6　齿轮1的y方向平移振动位移时域谱及频域谱Fig.6 The time-domain spectrum and the frequency spectrum of the translation displacement in y direction of gear 1

图7　齿轮1的z方向平移振动位移时域谱及频域谱Fig.7 The time-domain spectrum and the frequency spectrum of the translation displacement in z direction of gear 1

图8　齿轮1的耦合振动位移时域谱及频域谱Fig.8 The time-domain spectrum and the frequency spectrum of the composite displacement of gear 1

图7表明，摩擦力对齿轮1轴向振动的影响很小，这是因为摩擦力主要作用在垂直于啮合线方向上，与轴向垂直，因此其对齿轮轴向振动的影响很微弱。从图中还可看出，与其他两个方向的振动位移相比，齿轮1的轴向振动位移较小，这是因为本文建立的人字齿轮副动力学模型中两个斜齿轮副的参数赋值均相同，因而轴向力相互抵消，齿轮的轴向振动较小。

图8表明，摩擦力对啮合平面内平移-扭转耦合振动位移δy的影响很微弱，这与文献[5]的结论一致，进一步验证本文模型的正确性。

2.2齿面摩擦对系统混沌及分岔特性的影响

图9(a)和(b)分别为有无考虑齿面摩擦情况下齿轮副1啮合线上量纲一相对位移随频率的分岔图。

图9　齿轮副1的位移分岔图Fig.9 The bifurcation diagram of the gear pair 1

由图9所示，考虑齿面摩擦及不考虑摩擦两种情况下，系统均是通过倍周期分岔通道进入混沌状态。当啮频较低时，齿面摩擦对系统的分岔特性影响并不明显，系统的倍周期分岔在低频时较为清晰，但在高频时变得模糊，这是由于摩擦产生的时滞效应在高频段内表现得更为明显。与文献[12]的计算结果相比，本文中摩擦对人字齿轮副分岔特性的影响弱于直齿轮，这是由人字齿轮的啮合特性决定的。人字齿轮由一端逐渐进入啮合再逐渐退出啮合，轮齿的接触线被节线分为两部分，各部分接触线上的摩擦力方向相反，相互抵消。因而摩擦力对人字齿轮传动动力学特性的影响较直齿轮要小。

从图中可看出，随着量纲-频率的增加，系统依次经历了单周期、周期2、周期4以及周期8倍周期分岔，进入混沌运动状态。随着量纲-频率继续增加，系统由混沌运动状态通过倒分岔进入周期2运动状态，最终通过稳定吸引子锁相为单周期运动。

为进一步研究齿面摩擦对人字齿轮系统分叉特性的影响，分别给出了考虑齿面摩擦以及不考虑齿面摩擦时系统lyapunov指数随频率的变化图，如图11所示。图中可看出，不考虑齿面摩擦时系统进入混沌状态的量纲-频率为1.361，对应的输入轴转速为7 548 r/min；考虑齿面摩擦时系统进入混沌运动状态的量纲-频率为1.332，对应的输入转速为7 299.1 r/min。可知，齿面摩擦导致系统进入混沌运动状态的临界转速降低，即齿面摩擦导致系统提前进入混沌状态。系统进入混沌运动状态后，考虑齿面摩擦时系统的最大lyapunov指数小于不考虑齿面摩擦时，表明齿面摩擦导致系统的混沌程度有所降低。此外，图11中混沌区域中系统的最大lyapunov指数均存在负值，说明系统在混沌区域中存在着周期窗口。

3结论

(1) 建立了考虑齿面摩擦、时变啮合刚度、齿侧间隙、综合啮合误差等因素的人字齿轮副弯曲-扭转-轴向耦合非线性动力学模型。

图10　齿轮副1考虑齿面摩擦时在不同量纲一频率下的庞加莱截面图Fig.10 The Poincaré map of gear 1 under the different dimensionless frequency

图11　最大lyapunov指数随频率的变化图Fig.11 The diagram of the maximum lyapunov exponent varying with frequency

(2) 根据人字齿轮副的啮合特性，采用数值积分方法分析了齿轮的动态啮合力、摩擦力以及摩擦力矩。

(3) 采用了基于弹流润滑理论(EHL)的摩擦因数计算模型得到人字齿轮的摩擦因数。

(4) 分析了齿面摩擦对于系统振动位移以及分岔特性的影响。结果表明，齿面摩擦会加剧垂直啮合线方向的振动，同时会导致系统提前进入混沌状态且使系统的混沌程度有所降低。

参 考 文 献

[1] 王成,高常青,崔焕勇. 基于啮合特性的人字齿轮动力学建模与分析[J]. 中南大学学报:自然科学版,2012,43(8):3019-3021.

WANG Cheng,GAO Chang-qing,CUI Huan-yong. Dynamic modeling and analysis of double helical gears based on meshing characters[J]. Journal of Central South University:Science and Technology,2012,43(8):3019-3021.

[2] Yang F,Shi Z,Meng J. Nonlinear dynamics and load sharing of double-mesh helical gear train[J]. Journal of Engineering Science and Technology Review,2013,6(2):29-34.

[3] 郭家舜,王三民,王颖. 基于解析解的人字齿轮齿廓修形动态分析[J]. 航空动力学报,2013 (3):613-620.

GUO Jia-shun,WANG San-min,WANG Ying. Dynamic analysis of tooth profile modification to herringbone gears based on analytical solution[J]. Journal of Aerospace power,2013 (3):613-620.

[4] Velex P,Cahouet V. Experimental and numerical investigations on the influence of tooth friction in spur and helical gear dynamics[J]. Transactions-American Society of Mechanical Engineers Journal of Mechanical Design,2000,122(4):515-522.

[5] He S,Gunda R,Singh R. Inclusion of sliding friction in contact dynamics model for helical gears[J]. Journal of Mechanical Design,2007,129(1):48-57.

[6] Liu C,Qin D,Liao Y. Dynamic model of variable speed process for herringbone gears including friction calculated by variable friction coefficient[J]. Journal of Mechanical Design,2014,136(4):041006.

[7] 朱恩涌,巫世晶,王晓笋,等. 含摩擦力的行星齿轮传动系统非线性动力学模型[J]. 振动与冲击,2010,29(8):217-220.

ZHU En-yong,WU Shi-jing,WANG Xiao-sun,et al. Study on nonlinear dynamic model of planetary gear train sets with friction force[J]. Journal of Vibration and Shock,2010,29(8):217-220.

[8] Chowdhury I,Dasgupta S P. Computation of Rayleigh damping coefficients for large systems[J]. The Electronic Journal of Geotechnical Engineering,2003,8(0).

[9] Radzimovsky E,Mirarefi A. Dynamic behavior of gear systems and variation of coefficient of friction and efficiency during the engagement cycle[J]. Journal of Engineering for Industry,1975,97(4):1274-1280.

[10] Buckingham. Analytical mechanics of gear[M].New York:Dover,1949

[11] Xu Hai. Development of a generalized mechanical efficiency prediction[D]. The Ohio State University,2005

[12] 王三民,沈允文. 含摩擦和间隙直齿轮副的混沌与分叉研究[J]. 机械工程学报,2002,38(9):8-11.

WANG San-min,SHEN Yun-wen. Haos and bifurcation analysis of a spur gear pair with combined friction andclearance[J].Journal of Mechanical Engineering,2002,38(9):8-11.

[13] 王峰,方宗德,李声晋. 多载荷工况下人字齿轮传动系统振动特性分析[J]. 振动与冲击,2013,32(1):49-52.

WANG Feng,FANG Zong-de,LI Sheng-jin. Dynamic charateristics of a double helical gear under multi-load[J]. Journal of Vibration and Shock,2013,32(1):49-52.

[14] Sondkar P,Kahraman A. A dynamic model of a double-helical planetary gear set[J]. Mechanism and Machine Theory,2013,70:157-174.

[15] Bu Z,Liu G,Wu L. Modal analyses of herringbone planetary gear train with journal bearings[J]. Mechanism and Machine Theory,2012,54:99-115.

[16] Vaishya M, Singh R.Sliding friction-induced non-linearity and parametric effects in gear dynamics[J].J. Sound Vib.,2001,248(4):671-694.

[17] 盛冬平，朱如鹏，陆凤霞,等.多间隙弯扭耦合齿轮非线性振动的分叉特性研究[J].振动与冲击,2014,33(19):116-122.

SHENG Dong-ping,ZHU Ru-peng,LU Feng-xia. Bifurcation characteristics of bending-torsional coupled gear nonlinear vibration with multi-clearance[J]. Journal of Vibration and Shock,2014,33(19):116-122.

Dynamic characteristics analysis of double helical gear pairs considering teeth surface sliding friction

LU Feng-xia, WANG Hao-fei, ZHU Ru-peng, BAO He-yun, JIANG Hui-hui

(College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Abstract:A three-dimensional nonlinear dynamic model of a double helical gear pair with 16-DOF was established taking teeth surface sliding friction, time-varying meshing stiffness, gear backlashes and gear mesh errors into account. The dynamic equations of the system were established with Newton Second Law. The tooth meshing force, tooth friction and friction torque were calculated with numerical integration according to the meshing characteristics of the double helical gear pair. The teeth surface friction coefficient was calculated with the model based on EHL. The effects of teeth surface friction on the dynamic behaviors of the system were analyzed. The results showed that the teeth surface sliding friction can lead to increase in vibration displacements in the direction perpendicular to the line of action and decrease in vibration along the line of action; the bifurcation of the system becomes blurred at higher meshing frequencies and the chaotic motion of the system appears earlier and infirmly due to the effect of teeth surface friction. The study was helpful for the further understanding the effect of teeth surface friction on periodic vibration and nonlinear vibration of double helical gear pairs. The results provided a technical basis for the design of double helical gear transmission.

Key words:teeth surface sliding friction; double helical gear pair; chaos; bifurcation

基金项目：国家自然科学基金(51475226;51305196)

收稿日期：2015-02-25修改稿收到日期：2015-05-12

中图分类号:TH132

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.033

第一作者 陆凤霞 女，副教授，1972年4月生