无网格FEM-BEM法计算舱室空间声传递函数

刘延善， 曾向阳， 王海涛

(西北工业大学 航海学院，西安　710072)

无网格FEM-BEM法计算舱室空间声传递函数

刘延善， 曾向阳， 王海涛

(西北工业大学 航海学院，西安710072)

摘要：对于舱室空间低频声场计算问题，通常采用有限元法(FEM)或者边界元法(BEM)，但是当封闭空间内部存在其他物体，又需要考虑外部激励对内场的影响时，直接采用单一的前述方法不能满足建模计算要求，而且这些基于网格的方法在前处理、光顺化处理等方面都存在不足。针对这些问题，将有限元和边界元法结合，并将其无网格化，这对于封闭环境的声场预测是一种新的尝试。首先推导了无网格FEM-BEM计算模型，对微分方程的离散、形函数构造等细节进行了详细阐述，然后以实际算例对提出的方法进行了验证，结果表明，无网格FEM-BEM方法和SYSNOISE的计算结果保持一致；进一步与实测结果的对比表明，该方法在低频率范围内，各测点平均声压级相对误差在5.26%以内。这说明，该方法不仅适用于复杂问题的计算，同时还具有良好的计算精度。

关键词：有限元法；边界元法；无网格法；声传递函数

对于飞机舱室空间低频声场的数值计算，现有的研究多集中于有限元法(FEM)、边界元(BEM)法等[1]。对于简化的封闭空间，单一的有限元法或者边界元法可以满足计算要求[2-3]，但是当封闭空间内部存在座椅等物体时，一般只能采用有限元法进行分析[4]，而如果此时还需要考虑声空间外部的扰动对内部的声场影响时，则单一方法已无法满足需求[5]，需要结合有限元法和边界元法来进行计算。

无论是有限元、边界元，还是二者结合的方法，有效计算频率都受到网格密度的影响，对于复杂结构，还可能出现网格畸变问题。笔者所在课题组将力学领域的无网格法引入声学[6]，建立的声学无网格模型可以较好地克服这方面的问题。该方法去除了定义在求解域上的网格单元，前处理只要节点位置信息，可以方便地在求解域内布置节点，从而可以在局部求解问题上提升计算精度。不过，现有模型只考虑了声源位于舱内的情况[7]，且未考虑舱内存在其他物体的情况。

实际舱室声场研究中更关心外部声源对于复杂舱室结构内部声场的作用，因此，本文首先研究基于传统声学有限元法和声学边界元法相结合的准则来进行声场数值计算，在此基础上，将混合模型无网格化，提出一种无网格FEM-BEM模型。然后以一个矩形结构和一个圆柱结构为例，对其计算准确性进行初步检验。最后对一个小型舱段结构进行实验测试，进一步验证该模型的有效性。

1无网格FEM-BEM模型原理

在工程实际中，数值模型的计算本质上是偏微分方程的求解。首先针对描述问题的方程，通过加权余量法或者变分法将其转化为等效积分形式。其次通过选择合适的离散方式并施加相应的物理边界条件，可以将数值积分问题转化为线性方程组的求解。最后通过分配满足计算要求的积分点并选择合适的线性方程组求解方法，可得到各离散点处的声学参量信息。

本文中的问题是声激励处于结构外部，需要求解舱室结构内部的声场，这需要借鉴传统的FEM-BEM结合方法。图1为本文混合方法的原理示意图。首先，无网格化BEM用于计算结构外部声场，得到内部声场的边界信息，具体理论实现在后续第三节说明。其次，利用前一步所得边界信息，借助无网格化的FEM法可获得结构内部的任意位置的声场信息，具体理论实现在后续第二节说明。基于这种结合思路，可以求解结构在外部激励作用下的速度边界，进而可以得到内部任意位置的声学响应，由此可进一步求解其他的声学参量。为说明无网格混合方法，首先阐述无网格法的基本原理，其次分别对无网格FEM和无网格BEM算法实现进行说明。

图1　无网格FEM-BEM原理示意图Fig.1 Schematic diagram of Meshless FEM-BEM

1.1无网格法

无网格法的基本思想是将待求解问题的区域离散为多个有限数目的节点，采用节点的权函数或者核函数来表征节点及其邻域内的声学参量，即利用权函数来近似地表示影响域内的声场函数，进而形成与节点声场相关的系统方程，之后再离散求解。

无网格法目前有十余种，区别体现在所用的微分方程的等效积分形式和离散近似方案。基于微分方程等效积分的加权余量法是求解偏微分方程的一种十分有效的方法，无网格法也可以用加权余量法或变分法来建立整体求解的系统方程[8]。加权权函数选取的不同可以给出不同的加权余量方法。常见的权函数有配点法、最小二乘法、Galerkin法等。后续计算主要采用Galerkin加权余量法来构造系统方程[9]。

形函数[10]直接决定了微分方程的离散方式。与一般的方法不同，在无网格法中，形函数也称试探函数，它是定义在局部区域(支撑域)中的函数，只在其支撑域中有定义，而在其支撑域外为零，所以也称紧支试探函数。在二维问题中，支撑域一般取为圆形域或矩形域。如图2所示，在求解域Ω上，排布若干节点，各节点具有圆或矩形等几何外形构成的权函数影响域ΩI，节点处的声压大小可通过权函数对求解域中任意点的声参量作用产生不同程度的贡献。

图2　节点的圆形支撑域和矩形支撑域Fig.2 Nodal compacted supported domain

权函数是紧支函数，它只在对于节点xI生成的w(x-xI)≠0的局部区域有定义，而在其他区域为零。权函数有定义的局部区域一般称为紧支撑域。权函数与空间距离有关系，设

w(x-xI)=w(d)

(1)

在问题域内，某位置的待求声学参量p(x)可以由一组离散节点xI(I=1,2,…,n)与相对应的紧支函数NI(x)的线性组合近似表示为

(2)

式中，n是求解域中节点的总数，pI是函数p(x)在节点xI处的值，即p(xI)=pI。N和p分别为

N=[N1(x),N2(x),…,NN(x)]

(3)

p=[p1,p2,…,pN]T

(4)

对于任意位置处待求参量的求解，无网格法中需要对所有节点的贡献量进行一次计算，而不像有限元法只是叠加该位置所包围单元各节点的声学参量的贡献，从这一点看，无网格比FEM法计算量略多。但是在求解系统方程不同矩阵时，无网格不需要进行单元矩阵的组装过程。

本文采用移动最小二乘法近似来构造形函数[11]。利用上述原理，可以分别将有限元算法和边界元算法与无网格法结合，最后再实现二者的融合，下面分别叙述相应的理论实现。

1.2无网格有限元模型

如图3所示，假设一封闭空间体积为V，内壁总面积为S，其中S1为刚性边界面，S2为吸声边界面，S3为振动速度边界面，n为外法向导数。

图3　封闭空间示意图Fig.3 Schematic of the enclosed space

边界条件分别为：

S1边界上：

(5)

S2边界上：

(6)

S3边界上：

(7)

封闭声场内声压的计算属于非齐次边界条件的二阶偏微分方程的求解，使用Galerkin法，经过推导[6]可得到系统的有限元方程为：

(K+jρ0ωC-k2M)p=F

(8)

式中,K为刚度矩阵，C为阻尼矩阵，M为质量矩阵，F为载荷矩阵。对模型使用无网格法离散化，根据上文的理论可实现形函数的计算，代入系统方程后，各个矩阵计算形式为：

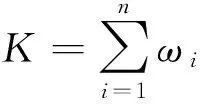
(9)

(10)

(11)

(12)

式中，n为模型总的域内积分点数目，l为代表阻抗边界的总积分点数，m为速度边界面所包含的积分点数，ωi为体积分和面积分离散化时的各积分点的权系数，N为无网格法构造的形函数[11]，在给定几何模型离散节点分布时，可直接求解系统方程中的不同矩阵。而前两种边界条件式(5)、式(6)可以通过阻尼矩阵C来添加，而速度边界条件式(7)则通过载荷向量F来实现，但这里的速度需要借助无网格BEM来求解，最后求解式(8)就可获得封闭空间内部任意点在给定边界条件和速度边界条件下的声传递函数。

当在实际中考虑内部空间座椅等问题时，通常认为声空间中包含座椅体积所占据的空间，声学模型中包含了座椅体积所占据的空间，这里是通过定义座椅空间部分为不同的流体材料来进行模拟计算的[4]。

1.3无网格边界元模型

对于外部声场，参考经典的Kirchhoff-Helmholtz方程

(13)

将问题边界采用无网格的方式进行离散，遍历所有节点(上文的P)，整理各离散公式后，可得到系统的线性方程组[12]：

Cp=GG·p-GH·p+F

(14)

式中，C为立体角矩阵，GG和GH为各积分点对不同节点的影响矩阵，F为表征声源影响的载荷矩阵，p为声压列向量，pI表示所有积分点对节点I的声压贡献(I=1,2,3,…,n)。它们的表示形式为：

(15)

(16)

(17)

(18)

(19)

F(ω)=jρωq(r0)G(P,r0)

(20)

(21)

式(17)、(19)为影响矩阵各元素计算公式，i，j分别表示节点序号和计算点序号，当遍历所有节点和计算点时，可得影响矩阵，再通过求解式(14)即可得到声场边界曲面上任意节点处的声压值，再通过法向阻抗与声压振速的关系即可得到边界节点上的振速及其他声学边界条件。

1.4无网格FEM-BEM算法

为更清楚地说明本文方法的实现过程，图4给出了本文方法的计算流程图。

图4　混合模型计算流程图Fig.4 Hybrid computing flowchart

对于Meshless BEM，在获得离散无网格模型后，遍历所有节点和积分点，计算式(14)中的各影响矩阵，同时设定相应的边界条件，最后求解式(14)可获得结构边界的振速信息。而对于Meshless FEM，经无网格离散化，遍历所有节点和积分点，计算式(8)中的不同矩阵，同时将施加所得的边界速度，最后求解式(8)所形成的线性方程组，可得到空间内任意位置的声场分布。

2数值算例及结果分析

2.1算例1

为了便于与商用软件对比，首先以一个圆柱壳结构(内部全空)的内部声场分析为例，如图5所示。源点位置(3,0,0)，体积速度取1。接收点位置从左到右分别为(0,0,0.9)、(0,0,1.5)、(0,0,2.1)，坐标原点固定在图中左端板的中心点处。圆柱壳半径为1 m，轴向长度为3 m。吸声条件是在所有壁面上具有阻尼边界条件，内壁声阻抗为40ρ0c0，外壁声阻抗取ρ0c0，其中ρ0=1.21 kg/m3，c0=344 m/s。声源的体积速度取为1，源信号为声脉冲信号[6]。

图5　圆柱壳结构示意图Fig.5 Schematic of the cylindrical shell structure

图6为无网格模型的节点分布示意图。取支撑域半径为1.5 m。根据所建立的无网格理论模型，计算了50 Hz～250 Hz频段内声源点到接收点的声传递函数，同时在SYSNOISE中进行相应的数值计算，计算的频带范围保持一致。图7为相应的各场点结果。

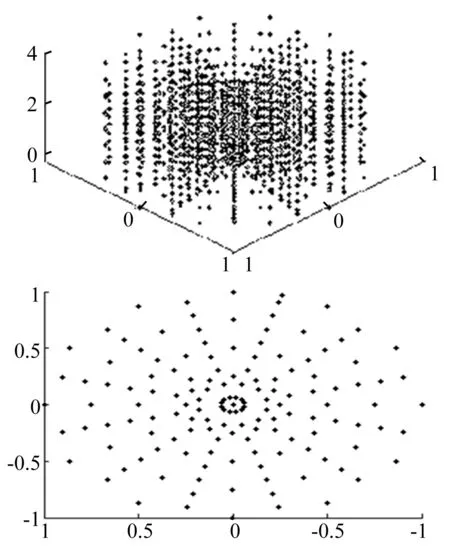
图6　圆柱形结构内部及截面无网格节点分布Fig.6 Nodal distribution of the meshless model

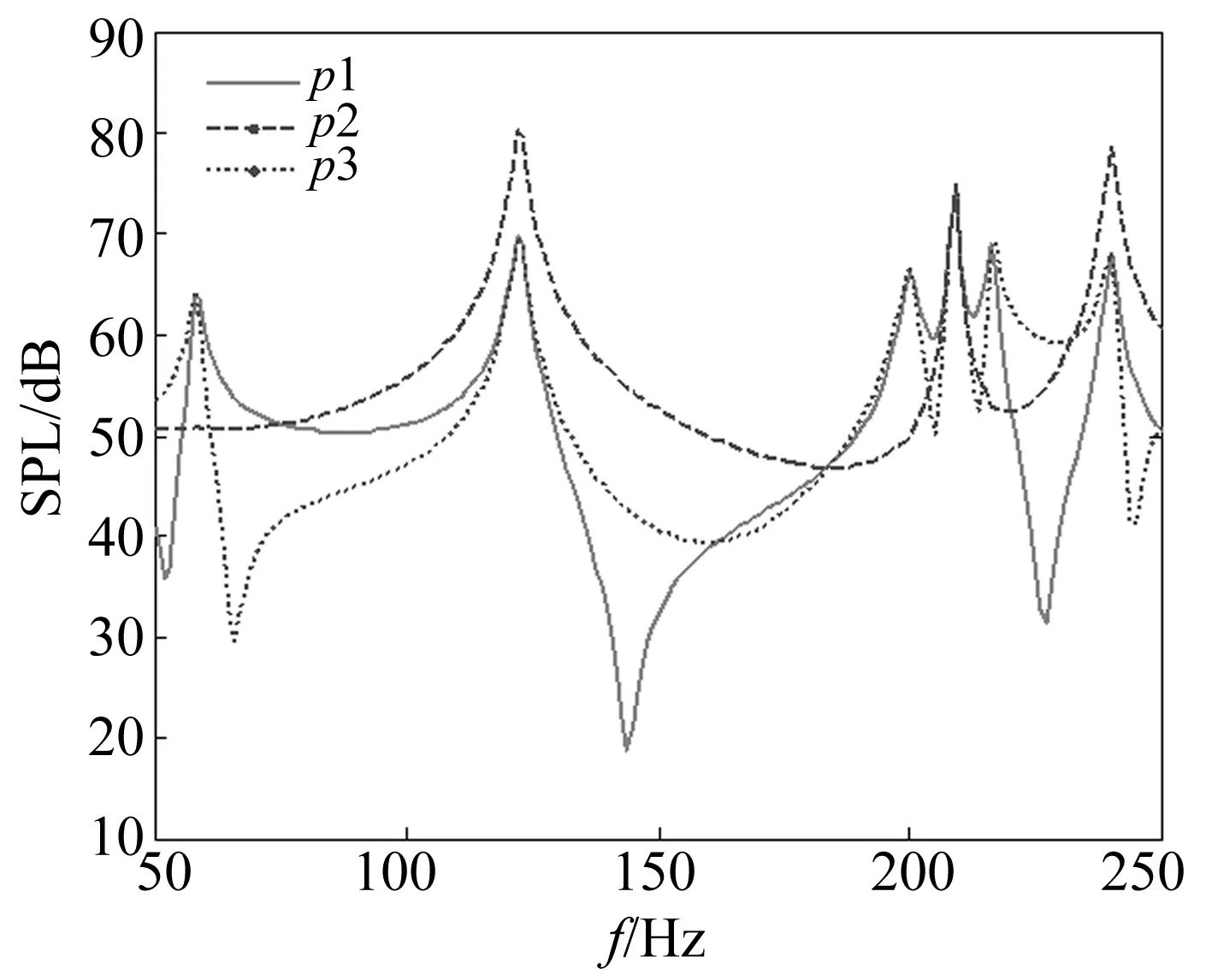
图7　各场点声传递函数Fig.7 Sound transfer functions at different field-points

对于场点p1、p2、p3，在特定的频率上都有极大峰值存在，如58 Hz、123 Hz、209 Hz、240 Hz，三个场点的平均声压级分别为79.1 dB、85.4 dB、79.4 dB。为验证本方法的准确性，将计算结果与商用软件SYSNOISE进行对比分析。图8为场点2的声传递函数，“MMFEMBEM”表示无网格FEM-BEM模型计算结果，“SYSNOISE”表示SYSNOISE软件得到的结果。

图8　p2场点幅值频率响应Fig.8 frequency response of the magnitude at p2

由图8可知，在250 Hz以下，两种方法获得的声压变化趋势非常接近。SYSNOISE得到的峰值频率位置为114 Hz、208 Hz和236 Hz，无网格法得到的峰值频率为114 Hz、208 Hz和239 Hz，二者得到的峰值频率保持一致，这些频率点也正与圆柱声腔主要的模态相对应。从平均声压级来看，无网格FEM-BEM模型的结果为88.9 dB，SYSNOISE的结果为92.6 dB，偏差为3.7 dB，相对于SYSNOISE的相对误差为4.0%。这些结果初步验证了无网格FEM-BEM模型的正确性。

2.2算例2

为验证本方法适用于舱室空间内部存在其他物体的情况，这里以矩形封闭空间内部放置矩形块为例进行仿真计算。选取的矩形封闭空间长1.0 m，宽1.1 m，高1.2 m。外壁面为刚性壁面，y=0的内壁面为吸声壁面，阻抗大小取10ρ0c0。声源为点声源，体积速度取1，坐标为(3,0,0)。测点坐标为(0.8,0.6,0.9)。矩形块底面中心与空间底面中心重合，长宽高分别为0.5 m、0.55 m、0.24 m，密度为22 kg/m3，其中声速为70 m/s，矩形封闭空间形状、声源点和测点的分布情况，如图9所示。

图9　矩形空间示意图Fig.9 Schematic of rectangular space

分别采用有网格FEM-BEM方法和无网格的FEM-BEM方法对上述模型进行计算。FEM-BEM的单元数为125，节点数为216，MMFEMBEM使用的节点数为216，积分点数为1 000，计算的频段均为0～300 Hz。图10为使用两种不同方法计算得到的声传递函数。

由图10可知，有网格FEM-BEM法和无网格FEM-BEM法所得的声传递函数结果很接近。从曲线整体走势来分析，在低频段二者的声传递函数变化趋势是一致的，在250～300 Hz范围内，两条曲线的差异有逐渐加大的趋势。分析原因，算例中所用模型的Schroeder频率[13]为302 Hz，根据文献理论可知，在Schroeder频率附近，是模态由稀疏变密集的过渡频带，严格地讲，在频率大于302 Hz时，波动方法已不再适用于求解该问题。以局部峰值频率的位置进行对比，在144 Hz、173 Hz、225 Hz、274 Hz处，两种方法得到的相应峰值是对应的，这几个点也正与该矩形空间的前几阶模态对应。总结起来，在低频率时，两种算法得到声传递函数基本保持一致，局部峰值频率点与相应的声模态阶次保持一致。

图10　声传递函数对比Fig.10 Comparison of transfer functions using different methods

3实验验证

为了进一步验证无网格有限元-边界元模型的正确性，在半消声室中对一个实际舱段进行了测量实验。测量系统如图11所示，图12为舱段模型。图13为传声器位置分布示意图。

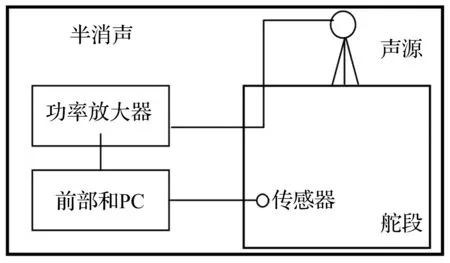
图11　实验测量系统Fig.11 Experimental measuring principle

图12　舱段模型Fig.12 Cabin model

图13　传声器位置截面分布示意图Fig.13 Distribution of microphones and source

以测点2为例。图14为数值计算和实验测试的1/3倍频带声压级结果的对比图。图15为测点结果的误差曲线。“fp2”表示测点2。

由图可知，在0～200 Hz时，数值计算结果和实验测量结果偏差在5 dB以内，而在200～500 Hz时，实验结果和数值仿真结果的误差大于5 dB，250 Hz时，声压级的误差最大。根据整体的声压级变化趋势，测点2的数值计算结果和实验测量结果基本保持一致。

图14　测点2声压级结果对比Fig.14 SPL comparison at fp2

图15　测点2声压级误差曲线Fig.15 SPL error at fp2

为计算各测点的平均声压级，将实验测得的1/3倍频带声压级结果进行对数平均，同时将数值仿真计算得到的各测点的声传递函数结果也作对数平均。表1为各测点的实验测量和数值计算总声压级结果和相对误差。

表1　数值计算与测量结果对比

根据表1中数据可求得7个测点的平均相对误差为5.26%，说明无网格FEM-BEM法与实际测试结果的总体偏差很小，这表明无网格FEM-BEM计算模型是正确的，可以用于外部声源作用下的封闭结构内部的声场计算问题。

4结论

本文提出一种无网格化的有限元和边界元相结合的方法来计算声传递函数，可用于复杂条件下的舱室内部声场分布预测。仿真算例和实测结果都表明，提出的方法在低频范围内，可以取得较为准确的预测效果，因而具有比单一的有限元或边界元法更宽的适用范围。在后面的研究工作，还将进一步分析本方法提升精度和计算效率方面的工作。

参 考 文 献

[1] Marburg S,Nolte B,Bernhard R J，et al. Computational acoustics of noise propagation in fluids:finite and boundary element methods[M]. Springer,2008.

[2] Ihlenburg F. Finite element analysis of acoustic scattering[M]. Springer,1998.

[3] Otsuru T,Tomiku R. Basic characteristics and accuracy of acoustic element using spline function in finite element sound field analysis[J]. Acoustical Science and Technology,2000,21(2):87-95.

[4] 李增刚,詹福良. Virtual. Lab Acoustics 声学仿真计算高级应用实例[M]. 北京：国防工业出版社,2010.

[5] Citarella R,Federico L,Cicatiello A. Modal acoustic transfer vector approach in a FEM-BEM vibro-acoustic analysis[J]. Engineering Analysis with Boundary Elements,2007,31(3):248-258.

[6] Wang H T,Zeng X Y,Chen L. Calculation of sound fields in small enclosures using a meshless model[J]. Applied Acoustics,2013,74(3):459-466.

[7] 王海涛,曾向阳,陈玲. 小尺度封闭空间无网格Galerkin声场数值计算方法[J]. 西北工业大学学报,2012,30(1):102-107.

WANG Hai-tao,ZENG Xiang-yang,CHEN Ling.An effective galerkin meshless model for calculating sound fields in arbitrarily shaped enclosures[J].Journal of Northwestern Polytechnical University,2012 30(1):102-107.

[8] Craggs A. Acoustic modeling:finite element method[J]. Handbook of Acoustics,MJ Crocker,Ed. New York:Wiley,1998:149-156.

[9] 王海涛,曾向阳. 周期结构声散射系数的无网格数值计算方法[J]. 计算物理,2013,30(2):229-236.

WANG Hai-tao,ZENG Xiang-yang. Meshless models for numerical calculation of scattering coefficients of periodic structures[J].Chinese Journal of Computational Physics,2013,30(2):229-236.

[10] 张雄,刘岩,马上. 无网格法的理论及应用[J]. 力学进展,2009,39(1):1-36.

ZHANG Xiong,LIU Yan,MA Shang.Meshfree methods and their applications[J].Advances in Mechanics,2009,39(1):1-36.

[11] 张雄,刘岩. 无网格法[M]. 北京:清华大学出版社,2004.

[12] Gunda R. Boundary element acoustics and the fast multipole method (FMM)[J]. Sound and Vibration,2008,42(3):12-16.

[13] Schroeder M R. The “Schroeder frequency” revisited[J]. The Journal of the Acoustical Society of America,1996,99(5):3240-3241.

Meshless FEM-BEM method for computing sound transfer function in enclosed spaces

LIU Yan-shan, ZENG Xiang-yang, WANG Hai-tao

(School of Marine Science and Technology, Northwestern Polytechnic University, Xi’an 710072, China)

Abstract:The finite element method(FEM) or boundary element method(BEM) is usually employed in sound field calculation of a cabin space at lower frequency, but a single method can not satisfy computing requirements of complex structures. These methods have some disadvantages, such as, lack of pre-processing and smoothing processing. Aiming at these problems, here, FEM and BEM were combined into a hybrid algorithm, and then transform it was converted into a meshless algorithm. It was a new approach for a sound prediction problem in enclosed environment. At first, the combined meshless FEM-BEM model was derived, and then the specific details including discretization of differential equations, construction of shape functions, nodal disposal, and were combined integral computing scheme were described. Finally, numerical simulations and tests were conducted to verify this method. The simulation results showed that the results using the proposed method agree well with those using SYSNOISE. The test results showed that the average relative error of each position’s sound pressure of a cabin space is less than 5.26%. These results showed that the proposed method not only is applicable for complex problems, but also has a good computation accuracy.

Key words:finite element method (FEM); boundary element method (BEM); meshless method; sound transfer function

基金项目：国家自然科学基金(11374241)；航空科学基金(20151553021)

收稿日期：2015-05-05修改稿收到日期：2015-11-09

通信作者曾向阳 男，博士，教授，1974年4月生

中图分类号:O422

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.002

第一作者 刘延善 男，博士生，1987年4月生