双质体振动磨动力学建模及参数优化

贾民平, 周　浩, 杨小兰, 刘极峰, 汪　震

(1.东南大学 机械工程学院,南京　211189； 2.南京工程学院 机械工程学院,南京　211167)

双质体振动磨动力学建模及参数优化

贾民平1, 周浩1, 杨小兰2, 刘极峰2, 汪震2

(1.东南大学 机械工程学院,南京211189； 2.南京工程学院 机械工程学院,南京211167)

摘要：针对多自由度振动磨系统建模困难以及动力学参数优化设计的需要，根据拉格朗日方程建立双质体振动磨6自由度动力学方程，利用数值分析方法分析了系统的动力学响应，并通过振动测试试验验证了模型的有效性。在振动微分方程的基础上研究了激振器转速对振动磨动力学特性的影响，仿真结果表明在一定范围内，转速越大，振动强度越大，但振动幅值越小。为了使振动磨产生更好的粉磨效果，对激振参数进行优化分析。利用模态分析获得双质体振动磨的固有频率和振型，分别从振动强度和共振频率两个角度确定系统激振器转速的上下限，得到转速的最佳取值范围。在实验室振动磨样机上进行参数优化后的粉磨试验，实验结果表明，改进后的振动磨机金刚石粉体产品d50达到0.27 μm，较之前有所细化，验证了参数优化具有一定的工程效果，为振动磨超微粉碎的动力学设计和产品开发奠定了基础。

关键词：振动磨;动力学模型;激振频率;参数优化;超微粉碎

振动磨作为一种细磨设备，通过激振装置驱动筒体作高频振动，使介质对物料实施冲击、摩擦和剪切等作用，实现被加工物料破碎、研磨、细化[1]。振动磨在超细粉磨中有着不可替代的作用，应用也越来越广泛。双质体振动磨是一种在传统振动磨基础上改进的新型粉磨设备，由上质体主振系统和下质体减振系统组成。较多的自由度和弹簧等使得双质体振动磨的动力学研究比传统振动磨更加复杂，因此有必要对振动磨的动力学特性作深入的研究。

国内外学者在振动磨动力学和参数优化等方面进行了相关研究工作。Gock等[2]建立振动磨机体和筒体运动的数学表达式，并研究振动磨能量散失函数和功率计算公式；Beenken等[3]建立偏心振动磨的3自由度运动方程，并与传统振动磨进行比较；江晓红等[4]推导了振动磨机的运动方程，分析了运动方程各参数对磨机运动轨迹的影响；刘政等[5]运用ProE和ANASYS对振动磨机体进行建模和初步分析，并对机体进行了局部优化。

但是上述研究对振动磨的建模简单，只考虑两个或三个自由度，也缺乏试验验证，同时对相关激振参数对粉磨效果影响鲜有研究。本文以实验室双质体振动磨样机为研究对象，建立6自由度系统动力学微分方程，进而研究激振频率对机体的影响，再从振动强度和模态分析相结合的角度对振动磨进行激振参数优化。

1双质体振动磨系统的动力学建模

1.1典型双质体振动磨结构及工作原理

典型双质体偏心振动磨结构如图1所示，主要包括筒体、振动电机、弹簧、研磨介质和物料以及质体板等。双质体偏心振动磨的最大特点是激振器即振动电机与筒体轴线不在一条直线上，而是处于筒体的侧边。振动电机由电动机和四组主副偏心块组成，改变电机转速，可以调整振动磨的激振频率；调整负偏心块和主偏心块的相位角，可改变激振力的大小，从而达到调整振幅大小的目的。下质体和隔振弹簧对底座起减振作用以降低基础载荷和噪音。

图1　典型偏心双质体振动磨结构图Fig.1 Typical structure of double masses vibration mill

振动磨物料和研磨介质装入弹簧支撑的磨筒内，由电动机驱动偏心激振装置高速旋转，从而产生惯性离心力使上质体及部件作一定频率和振幅的连续受迫振动。筒体的受迫振动使被磨物料受到研磨介质强烈的冲击、挤压、剪切及研磨等作用，使物料的弹性模量降低并产生缺陷和微裂纹扩展，达到粉碎物料的目的。

1.2双质体振动磨物理模型

实验室振动磨与典型双质体磨机有一定的区别，振动电机采用下置式而非左右偏置，这样可以省去平衡装置，缩短整体尺寸，减轻振动磨重量。故可以用与筒体轴线正交平面内的有阻尼6自由度强迫振动来描述实验室振动磨样机，如图2所示。6个自由度分别表示为上、下质体在x方向和y方向的平动以及绕其质心的转动，其中，φ1为偏心块绕竖直方向的转角，X1O1Y1为固联于上质体质心的随体坐标系，X2O2Y2为固联于下质体板质心的随体坐标系，XOY为绝对坐标系。

图2　实验室双质体振动磨6自由度动力学模型Fig.2 The dynamic model of six degree of freedom

1.3振动微分方程的建立

1.3.1系统动能

根据Lagrange方程，该系统的动能包括上质体T1、下质体T2和偏心块的动能T3，可表示为：

(1)

(2)

(3)

式中:偏心块速度可表示为：

(4)

式中，H为偏心块转动中心距上质体参考点距离，a为偏心块的回转半径。

1.3.2系统势能

系统的势能由主振弹簧和减振弹簧的弹性势能组成，不包括重力势能和弹簧静变形的势能。

1) 下质体减振弹簧的弹性势能计算

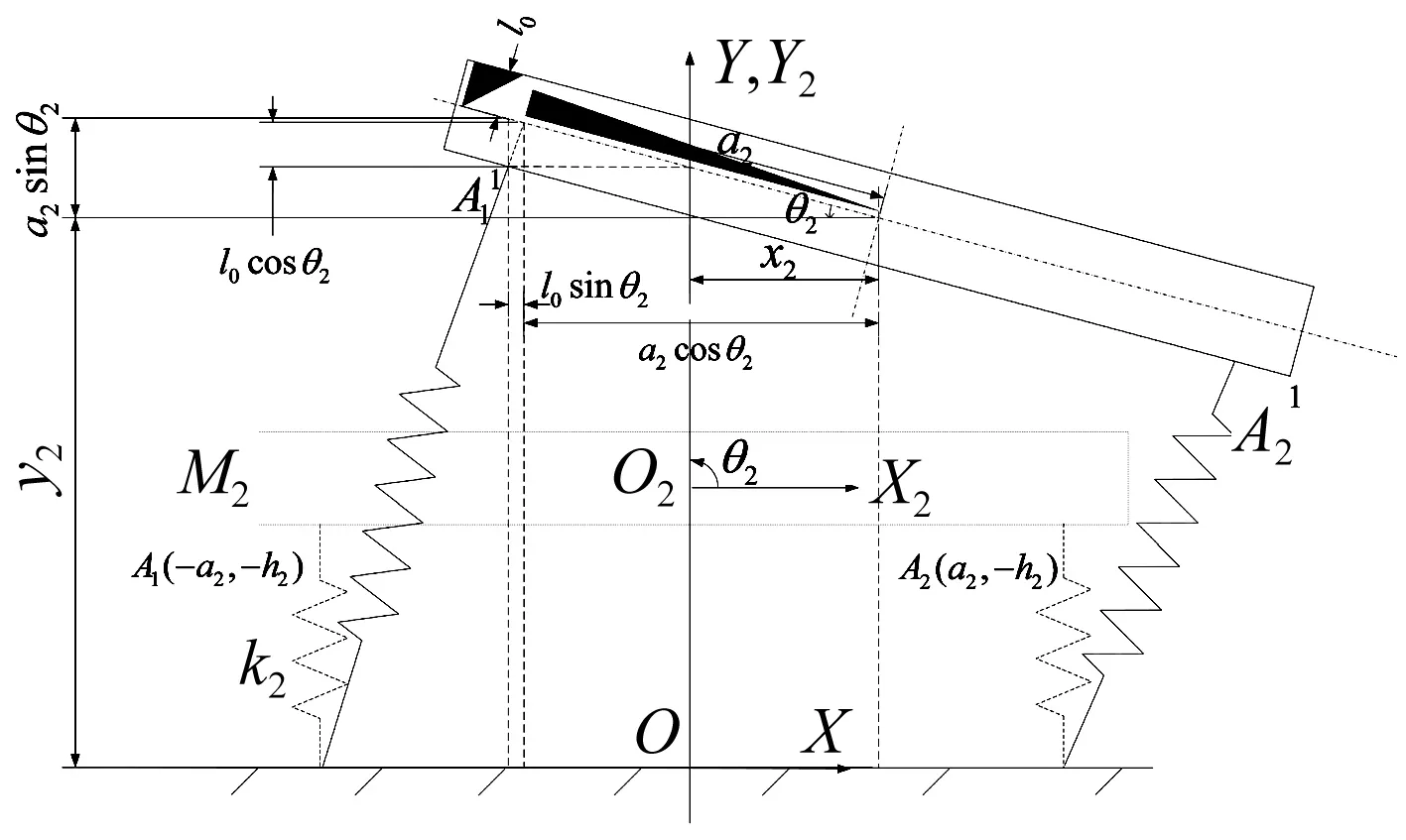
图3　下质体弹簧弹性势能分析简图Fig.3 Strain energy of lower spring

下质体弹簧弹性势能分析结构简图如图3所示。弹簧中A1点初始状态在绝对坐标系XOY中的坐标为A1(-a2,h2),则A1点在工作状态下的绝对坐标为：

(5)

因此A1点的变形为：

(6)

同理可得A2点的变形，容易得到下质体减振弹簧的弹性势能表达式为：

2) 上质体主振弹簧的弹性势能计算

上质体弹簧弹性势能分析结构简图如图4所示。弹簧中B1点初始状态在X2O2Y2坐标系下的坐标为B1(-a1,h1)，则B1点在工作状态下的绝对坐标为：

(8)

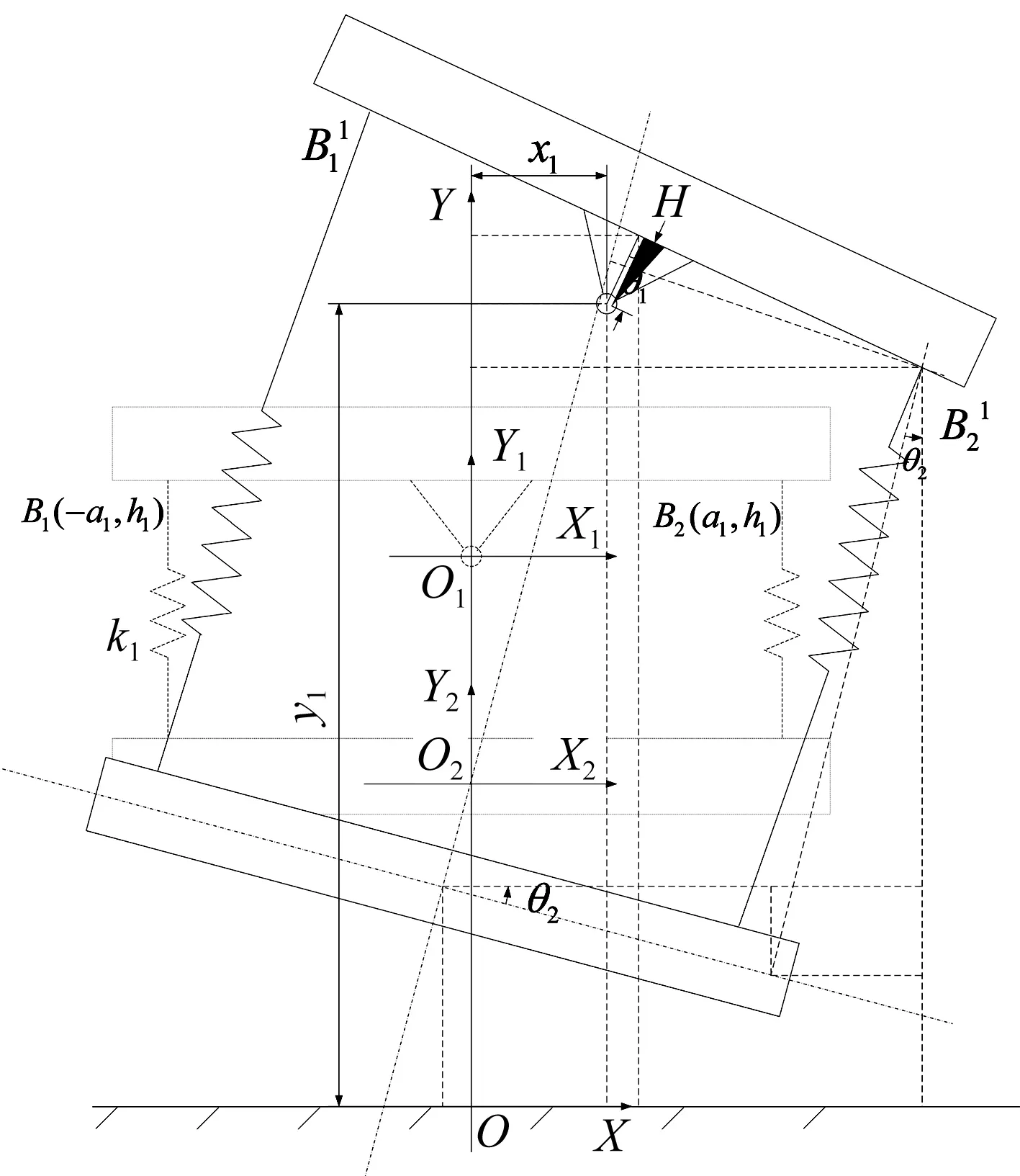
图4　上质体弹簧弹性势能分析结构简图Fig.4 Strain energy of upper spring

若B1在X2O2Y2坐标系下坐标为(xB1,yB1)，则

B1点变形量为：

(10)

同理可得B2点的变形，则主振弹簧的弹性势能：

(11)

综上，系统的总势能为：

U=U1+U2

(12)

1.3.3系统能量散失函数

能量散失函数D可表示为：

(13)

式中,ci为由阻尼比ξ构成的阻尼系数

(14)

1.3.4振动微分方程组

将振动磨系统的总动能表达式和总势能表达式对各个自由度求导数，代入上面的拉格朗日方程。整理可得由下列6个方程组成的微分方程组：

(l12-a12)sin(2θ1-2θ2)-(y1-y2)2sin2θ2]-2sin(θ1-θ2)(k1xa12+k1yh1H)+(k2x-k2y)sin2θ2(l02-a22)+

(15)

式中，j1、j2为上、下质体的转动惯量；k1x、k1y为主振弹簧在径向和轴向的刚度系数；k2x、k2y为减振弹簧在径向和轴向的刚度系数；θ1为偏心块绕上质体垂直向下方向的转角，并规定顺时针方向转动取正值；2a1、2a2为上、下质体板的宽度；h1为系统静止时上质体弹簧顶点至坐标系X2O2Y2水平轴的距离；h2为系统静止时下质体弹簧顶点至绝对坐标系XOY水平轴的距离；2l1、2l2为上、下质体板的厚度；ci为各个方向的阻尼系数；ξ为阻尼比。

2振动磨动力学分析及试验验证

2.1系统动力学仿真分析

振动磨样机激振器转速为1 000 r/min，最大激振力10 kN。将表1中磨机相关参数代入动力学方程组(15)，利用数值分析方法可得振动磨在恒定转速下的动力学响应。其中上、下质体在水平、垂直和转动方向的位移曲线以及中心运动轨迹如图5、图6所示。由图5可知，恒定转速激振下，振动磨在开机阶段会产生一定的晃动，稳定后会产生周期性的简谐波响应，频率为激振器的激振频率，且筒体中心轨迹为椭圆。对比两幅图可以看出，相对于上质体，下质体的位移和振动幅度很小，垂直方向振幅为上质体的20%，水平方向仅为上质体的17.24%，即下质体运动对振动磨整体影响较小，故进一步分析时以上质体动力学响应为主。

表1　振动磨样机相关参数表

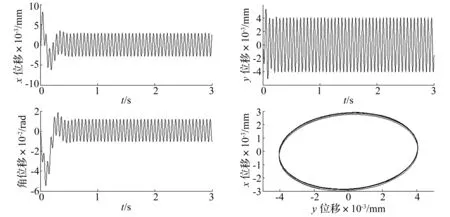
图5　振动磨机上质体在三个方向的位移曲线及中心轨迹Fig.5 The curves of upper body’s displacement in three direction and the center track

2.2双质体振动磨振动信号测试

实验设备包含振动磨样机、传感器、信号采集系统，振动磨尺寸参数、激振器频率等与仿真相同，使用压电加速度传感器。在实际振动磨样机实验中，仿真参考点在设备中无法直接测量，可以根据上质体上的测点来间接验证模型的准确性。先计算出测点相对于参考点的距离和角度，结合参考点的运动方程和转动方程，推导出实测点的位移方程，进一步求导可得加速度方程，与实测信号进行对比，进而验证理论模型的有效性。

利用DHDAS5920_1394动态信号采集分析系统和压电式加速度传感器，在采用频率为2 000 Hz下分别测量振动磨样机筒体和上质体板上四个便于安装传感器位置的加速度值，4个测点的具体位置如图7所示。分别将实际测量值与该点仿真值进行对比，具体如下图8所示。

从上述四个测点加速度对比图可以看出，振动磨各点加速度周期为60.46 ms，频率为16.54 Hz，对应于振动磨激振器所在轴的转频，与仿真情况一致。波形和振动幅值与仿真信号基本相吻合。

图6　振动磨机下质体在三个方向的位移曲线及中心轨迹Fig.6 The curves of underbody’s displacement in three direction and the center track

图7　振动磨试验上质体测点示意图Fig.7 Sketch of measuring points

3振动电机转速优化

振动强度(振幅和激振角速度的平方之积与重力加速度的比值)是衡量振动磨粉磨效果的一个重要技术参数，提高振动强度可以使物料在筒体内经较短的时间获得较佳的细化效果[6]。在优化设计中，可通过振动强度约束来保证系统的性能指标，考虑到振动磨结构的复杂性和高速运转的危险性，要求激振参数满足安全需求。

图8　四个测点加速度实测值(叉点)与仿真值(实线)对比图Fig.8 Comparison between real values and simulation values

本文从振动强度和模态分析两个角度对磨机振动电机转速分别进行优化设计，转速直接影响振动磨系统的振幅和振动强度，优化的目标是振动磨达到粉磨所需强度，提高粉磨效率，同时远离共振区，确保安全运转。

3.1转速对振动磨动力学响应影响分析

振动电机转速可以通过变频器调节，其值是振动强度的重要影响因素，同时转速变化也会对振动磨振幅产生影响。通过振动微分方程组可得不同转速下振动磨振幅和振动强度值如图9所示。

图9　振动电机转速对上质体振幅和振强的影响Fig.9 Vibration amplitude and intensity with the rotation speed

从图9可以看出，在远超共振区工作的振动磨，振幅随着激振频率的增大而减小，但振动强度在不断变大，且变化趋势较为明显。当转速为600 r/min时，振强约为2，为低振强；当转速达到1 800 r/min时，振强值已经超过10，属于高振强。可以清楚地看出，改变激振频率，振强变化范围大。

上述分析表明，激振频率对振动磨动力学响应影响显著，调节激振频率可以在较大范围内实现振强值的改变。实践证明，当振动强度大于6时，磨机才能产生细磨作用[6]，结合图7中振强与转速关系曲线，即转速要大于1 300 r/min时振动磨才能达到颗粒超微粉磨所需的动力学要求。但由于转速变大，振幅变小，对粉磨会产生不利影响，因此不能无限提高转速来追求颗粒细化，需要对转速选取的上限进行研究。

3.2振动磨模态分析

振动磨属于高振强设备，它的工作状态与结构模态有很大关系。因此在对激振参数优化时，有必要对系统固有频率和振型进行研究，控制有利振动，避免进入共振区。

振动磨模型是在Pro/Engineer软件中建立的，进而导入ANSYS Workbench中，并对模型进行了部分简化，如螺栓、圆角等，定义材料属性，划分网格，确定边界条件。求解可得振动磨系统的前八阶模态频率和振型，见表2和图10所示。第六阶振型是振动磨上质体上下振动，这是粉磨工作过程中主要的振动形式，故振动磨工作频率应落在第六阶与第七阶固有频率之间。根据振动利用工程知识和相关学者研究经验[10]，振动粉磨设备频率选择应介于1.2f6和0.25f7之间，即转速范围在410～1 690 r/min之间。

结合从振动强度和模态分析的两个角度得出的频率范围，得出优化后实验室振动磨样机电机转速应介于1 300～1 690 r/min之间。

表2　振动磨各阶固有频率和振型描述

图10　振动磨第6阶振型图Fig.10 The sixth step vibration shape

4振动磨样机试验与分析

实验室以筒体尺寸φ200 mm×400 mm型振动磨作为样机，最大激振力10 kN，功率0.75 kW。筒体内放入平均粒度10 μm的金刚石粉体，并放入一定数量的锰钢球介质。按照得出的转速最佳取值范围，通过变频器实现振动控制，累计粉磨时间100小时。试验结束后，通过检测得到粉体产品的电镜扫描图像如图11所示，样品前50%的粒度分布见表3。

图11　粉体电镜扫描图像Fig.11 Image of scanning electron microscope

上述检测结果表明，转速优化后的粉体颗粒尺寸d50达到0.27 μm。而在转速没有优化情况下，振动磨粉磨产品的粒度分布见表4所示。从图中可以明显看出，振动磨在转速没有优化前其d50的约为2.52 μm。

表3　优化后粉体颗粒粒度分布表

表4　优化前粉体颗粒粒度分布表

对比表3和表4可知，转速优化后产品颗粒较之前平均粒度明显降低，细化效果显著，说明在较短时间内获得了良好的粉磨效果，验证了参数优化具有一定的工程应用价值。这证实了对振动磨转速优化不仅可以进行超微粉磨作业，细化颗粒，而且能够提高生产能力，缩短工作时间。同时也应该注意到，此时的转速不宜太高，适当的振动频率不仅有利于降低粉磨功耗，而且有利于延长轴承等高速旋转设备的寿命。

5结论

(1) 打破了振动磨建模分析时未考虑质体转动情况的不足，建立了双质体振动磨的动力学模型和六自由度动力学方程，利用数值方法研究了系统的动力学响应，并利用振动测试试验验证了模型的有效性；

(2) 基于已经建立的系统振动微分方程组，分析了转速变化对磨机振动幅值和振动强度的影响。在一定范围内，转速越大，振动强度越大，而振幅变小，使粉碎难度加大。通过模态分析方法，获得了振动磨的固有频率和振型，从利用有益振动、避免共振角度确定了转速选取的上限，得到了振动磨系统优化后的转速范围；

(3) 粉磨试验研究表明，优化后的电机转速对振动磨粉磨颗粒细化起到有效的促进，提高粉磨效率，并且能够降低振动磨粉磨设备的能耗。试验结果对双质体振动磨的参数选取提供一定的参考。

参 考 文 献

[1] 张世礼. 特大型振动磨及其应用[M]. 北京：冶金工业出版社，2007.

[2] Gock E，Kurrer K E. Eccentric vibratory mills-theory and practice[J]. Power Technology，1999，105：302-310.

[3] Beenken W，Gock E，Kurrer K E. The outer mechanics of the eccentric vibration mill[J]. International Journal of Mineral Processing，1996，44：437-446.

[4] 江晓红，张永忠，丁江. 振动磨机的振动力学模型及运动分析[J]. 中国矿业大学学报，1998，27(2):192-195.

JIANG Xiao-hong,ZHANG Yong-zhong,DING Jiang. Dynamic model and motion analysis of vibration mill[J].Journal of China University of Mining & Technology,1998，27(2):192-195.

[5] 刘政，熊运星，党继辉. 振动磨机机体有限元分析及局部优化[J]. 煤矿机械，2004，10:41-42.

LIU Zheng,XIONG Yun-xing,DANG Ji-hui. The FEA and local optimization for the vibration mill’s block[J]. Coal Mine Machinery,2004，10:41-42.

[6] 陶珍东，郑少华．粉体工程与设备[M]．北京：化学工业出版社，2010.

[7] Bernotat S. Vibration mill results in the light of stress intensity and number of stressing events[J]. International Journal of Mineral Processing，2004，74(Sup)：119-122.

[8] 刘极峰，杨小兰. 交叉轴式螺旋垂直振动提升机结构参数研究与优化[J]. 振动工程学报，2004，17：1101-1102.

LIU Ji-feng,YANG Xiao-lan. Study and optimization on structural parameter of spiral vertical vibration hoist by cross axles[J]. Journal of Vibration Engineering,2004，17：1101-1102.

[9] Nygards T，Berbyuk V. Multibody modeling and vibration dynamics analysis of washing machines[J]. Multibody System Dynamics，2012，27(2)：197-238.

[10] 郭天德，段碧霞，李爱国．WGM-3型超细振动磨机振动参数控制[J]．中国粉体技术，1999，5(1)：1-6.

GUO Tian-de,DUAN Bi-xia,LI Ai-guo,et al. Control of vibrational parameter for type of WGM-3 superfine wave grinding mill[J]. China Powder Science and Technology,1999,5(1)：1-6.

[11] Wei X H，Nie H. Dynamic analysis of aircraft landing impact using landing-region-based model[J]. Journal of Aircraft，2005，42(6)：1631-1637.

[12] Pinheiro A P，Kerschen G. Vibrational dynamics of vocal folds using nonlinear normal modes[J]. Medical Engineering and Physics，2013，35(8)：1079-1088.

Dynamic modeling and parametric optimization for a double-mass vibration mill

JIA Min-pin1, ZHOU Hao1, YANG Xiao-lan2, LIU Ji-feng2, WANG Zhen2

(1. School of Mechanical Engineering, Southeast University, Nanjing 211189, China;2. School of Mechanical Engineering, Nanjing Institute of Technology, Nanjing 211167, China)

Abstract:Aiming at the needs of modelling and dynamic parametric optimization design of vibration grinding systems with multi-DOF, the dynamic equations with 6-DOF of a double-mass vibration mill based on Lagrange equation were established. The dynamic response of the double mass vibration mill was analyzed using the numerical analysis method and the model was verrified to be effective with vibration tests. The relationship between the double mass vibration mill’s dynamic characters and the rotating speed of its exciter was studied with the help of the established model. It was shown that the larger the rotating speed, the bigger the vibration intensity, but the smaller the vibration amplitude. In order to achieve the better effect of grinding, the excitation parameters were optimized. With the help of modal analysis, the natural frequencies and vibration modal shapes of the system were obtained. The upper limit of the rotating speed was determined with the resonance frequencies and the lower limit was determined with the vibration intensity. Then, the optimal range of the rotating speed was determined. A grinding test with diamond powder was conducted on the model machine. The result showed that the average size of output powder is 0.27 μm, it meets the requirements of ultrafine powder. This optimization laid a foundation for dynamic design and product development of vibration mills for ultrafine comminution.

Key words:vibration mill; dynamic model; excitation frequency; parametric optimization; ultrafine comminution

基金项目：国家自然科学基金(51375221);江苏省自然科学基金(BK2012865);国家级大学生创新训练项目(201411276009Z)

收稿日期：2015-01-29修改稿收到日期：2015-05-04

中图分类号:TH113.1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.010

第一作者 贾民平 男，教授，博士生导师，1960年9月生

E-mail:mpjia@seu.edu.cn