海洋二号卫星微波辐射计的动平衡设计仿真与试验

王朋朋， 牛宝华， 艾永强， 王三民

(1. 中国空间技术研究院西安分院，西安　710100; 2. 西北工业大学 机电学院，西安　710072)

海洋二号卫星微波辐射计的动平衡设计仿真与试验

王朋朋1， 牛宝华1， 艾永强1， 王三民2

(1. 中国空间技术研究院西安分院，西安710100; 2. 西北工业大学 机电学院，西安710072)

摘要：为了实现卫星的高精度姿态控制，需要对以辐射计为代表的大型回转载荷进行严格的动平衡设计仿真与试验。结合海洋二号卫星研制需求，在产品设计初期开展了针对微波辐射计的动平衡设计仿真，以提供优化产品结构和布局的依据。为了评估空气环境对动平衡配平的影响，进行了辐射计动平衡配平的风阻影响分析。考虑了重力因素、在轨热变形和无重力下轴承径向游隙变化对辐射计动平衡的影响。最终在真空环境下开展了针对辐射计的动平衡试验，以很小的配重质量，实现了微波辐射计的配平。

关键词：微波辐射计;大型回转载荷;动平衡

微波辐射计是海洋二号卫星的重要载荷，其结构构型为大型回转体，回转部分质量在整星质量中占相当大的比例。卫星入轨后辐射计需要进行持续圆锥扫描观测，由于其质量分布不均匀，会引入静不平衡和动不平衡，产生惯性力和惯性力矩，对卫星的飞行姿态产生较大影响。为了实现卫星的高精度姿态控制(要求卫星三轴指向精度优于0.1°，姿态稳定度优于0.003 °/s，测量精度优于0.03°)[1-3]，需要对以辐射计为代表的大型回转载荷进行严格的动平衡设计仿真与动平衡测试和配平。

动平衡的概念最早出现在转子动力学领域，其目标是减少转子挠曲、减少振动和轴承动态反力。根据转子工作转速与一阶临界转速的关系，可以分为刚性转子动力学和挠性转子动力学。为了实现转子的平衡，工程界提出了多种动平衡的理论和方法，刚性转子有力平衡法和两平面影响系数法等，挠性转子有模态平衡法、影响系数法、综合平衡法等。各种动平衡理论及实现方法在航空发动机、直升机旋翼、智能机器人等领域得到了广泛应用[4-10]。空间微重力环境下，回转载荷转子轴承的支承和润滑状态与地面大不相同，对其动平衡特性提出了更为苛刻的要求，回转载荷成为影响整个航天器寿命的关键。按照回转载荷100 r/min的设计转速，对于5年寿命的海洋卫星，其总计转动2.63×108圈，如果不对其不平衡量进行控制，将会引起转子轴承的磨损，导致扰动载荷的增加，危害航天器安全。国内外含回转体航天器在发射之前均对其动不平衡量进行了严格的测试与控制，图 1为美国深度撞击号彗星探测器和全球降水测量航天器微波成像仪所进行的动平衡测试[11]。

图1　航天器动平衡测试Fig.1 Dynamic balancing test of spacecrafts

结合海洋二号卫星研制需求，在产品设计初期开展了针对微波辐射计的动平衡设计仿真，以提供优化产品结构和布局的依据。为了评估空气环境对动平衡配平的影响，进行了辐射计动平衡配平的风阻影响分析。考虑了重力因素、在轨热变形和无重力下轴承径向游隙变化对辐射计动平衡的影响。最终在真空环境下开展了针对辐射计的动平衡试验，以很小的配重质量，实现了微波辐射计的配平。

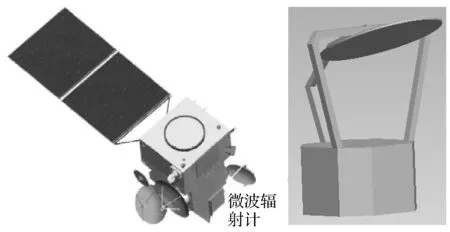
图2　微波辐射计星上布局及结构构型Fig.2 Microwave radiometer configuration and its layout on satellite

1静平衡与动平衡

当质量M、偏心距e的回转体以角速度ω绕旋转轴O-Z轴作等速旋转时，其在旋转中心O处产生的惯性力P和惯性力矩N分别表示为[12]：

(1)

式中，Izx表示回转体对坐标轴z轴、x轴的惯性积，Iyz表示回转体对坐标轴y轴、z轴的惯性积。

式(1)中，P和N随回转体旋转而改变方向，因此对于旋转轴的支承机构作用有动载荷并成为产生机械振动的根源。要使这些有害的P和N变为零，回转体的质量分布需要满足以下条件：

1)e=0即需要回转体的质心在旋转轴上。此时，无论ω取任何值，惯性力的合力都为零，这种状态称为静平衡状态。但是在这种情况下，一般都会残留惯性力矩N，所以回转体旋转轴支承机构依然受惯性力矩作用。

2)Izx=Iyz=0即要求回转体对Z轴有关的惯性积均为零。这意味着回转体的一根主惯性轴应与旋转轴重合。这种情况下，坐标原点可以在坐标轴上取任意位置，对于任何z的取法，Izx=Iyz=0都包含有e=0的条件，其结果也就要求通过回转体质心的主惯性轴与旋转轴重合，这就是动平衡的条件。如果能够满足这一条件，则旋转轴不受任何力和力矩的作用，并且支承上没有动载荷作用，因此也没有振动现象的出现。这种状态称为完全平衡状态。

因此，静平衡与动平衡存在如下关系：动平衡一定是静平衡的，静平衡往往不是动平衡的。

2微波辐射计的动平衡设计仿真

为了改善不规则回转体的静平衡和动平衡特性，就需要修改回转体运动部分的质量分布，以避免不平衡力和力矩的产生。目前的动平衡试验是在动平衡机上进行的，首先在产品上选择配平平面和配平半径，根据动平衡机的提示在相应的位置和角度逐步添加或去除配重，使得产品的动平衡特性逐步达到设计要求。由于动平衡试验的事后性，配重位置及大小的选取会受到多种条件的限制。因此，需要在产品设计初期，对产品的动平衡特性有定性了解，如配重的质量和位置信息，从而提供优化产品结构和布局的依据。图3给出了对微波辐射计进行动平衡仿真配平的示意图，仿真中选取了两个平衡配重基准面，分别位于辐射计高频箱的上下外表面。

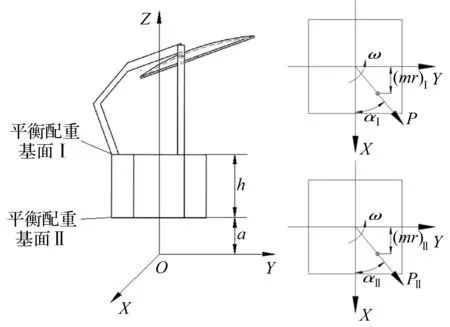
图3　微波辐射计配平平面示意图Fig.3 Balancing plane of microwave radiometer

假定两个平衡配重基准面上需要添加的配重质径积和对应的相位角分别为(mr)Ⅰ、αⅡ和(mr)Ⅱ、αⅡ，则实现辐射计的动平衡需要以下等式同时成立：

要注意把足球文化和我国的校园文化、体育文化以及传统文化融合起来，让学生从内心深处喜欢足球，参与足球，欣赏足球。

(2)

式中，Fx、Fy和Mx、My分别为辐射计旋转中心处受到的扰动力和扰动力矩，其具体值可以通过对微波辐射计的动平衡ADAMS仿真获得[13]。图4给出了动平衡设计前后，辐射计旋转中心处的扰动力和扰动力矩随时间的变化曲线对比。动平衡设计后，结构旋转中心处所受的扰动力和扰动力矩明显减小，辐射计动平衡特性极大改善。

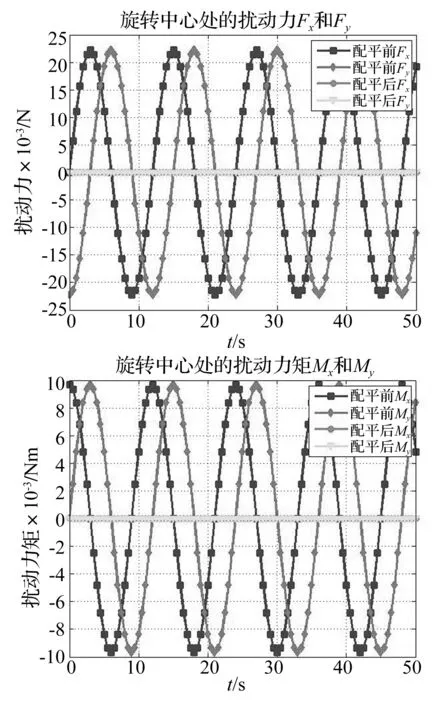
图4　动平衡设计前后旋转中心处的扰动力和扰动力矩对比Fig.4 Disturbance force and moment at rotate center before and after dynamic balancing

3风阻的影响

由于微波辐射计在轨工作处于真空环境中，但是地面试验在空气环境中进行，反射器在动平衡配平过程中会受到风的扰动造成配平数据不稳定或无法实施配平，为了评估空气环境对动平衡配平的影响，进行了辐射计动平衡配平的风阻影响分析。

3.1风压分布分析

微波辐射计工作时，在流场中绕中心轴旋转，反射器表面会承受风压作用。由于反射器前后表面的构型差异及安装俯仰角的存在，反射器前后表面所承受的风压是不平衡的，风压的不平衡会形成合力和合力矩，会在微波辐射计旋转坐标系三个坐标轴处形成力偶，风压不平衡引入的力偶与辐射计原有的动不平衡量叠加，会导致动平衡试验偏差。微波辐射计转速为60 r/min时，辐射计反射器前后表面的压强云图如图 5所示，图中给出的压强值为与标准大气压的差值，如果压强值为负值表示该处气压小于标准大气压，正值表示该处气压大于标准大气压。

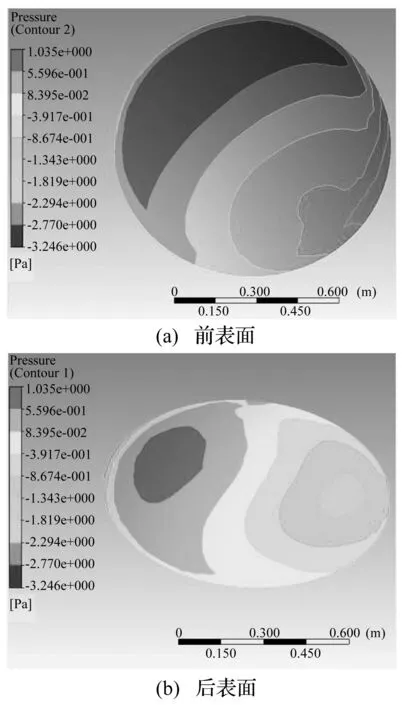
图5　微波辐射计反射器前后表面的压强云图Fig.5 Pressure distribution on front and back surface of microwave radiometer

3.2风阻合力和合力矩

辐射计反射器坐标系O0X0Y0Z0与旋转坐标系OXYZ的关系如图 6所示，假定反射器坐标系原点在旋转坐标系中的坐标值为(a,b,c)，则存在如下坐标转换关系：

(3)

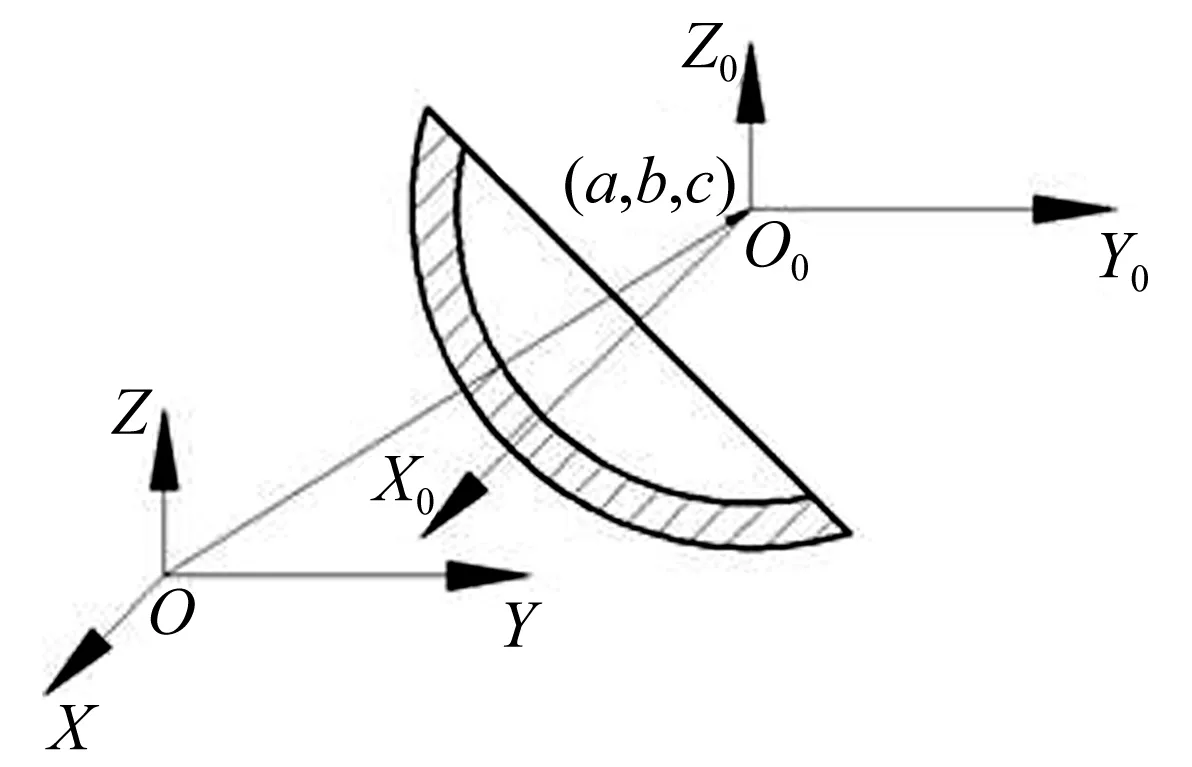
图6　反射器坐标系与旋转坐标系相对关系Fig.6 Relationship between reflector coordinate and rotate coordinate

假设反射器的曲面方程为f(x,y,z)=0，曲面上任意点(x0,y0,z0)处的压强值为p(x0,y0,z0)，该点处的风阻力在坐标轴三个方向的分量可近似表示为

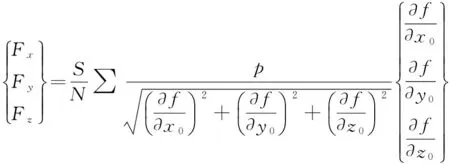
总的风阻力矩表示为

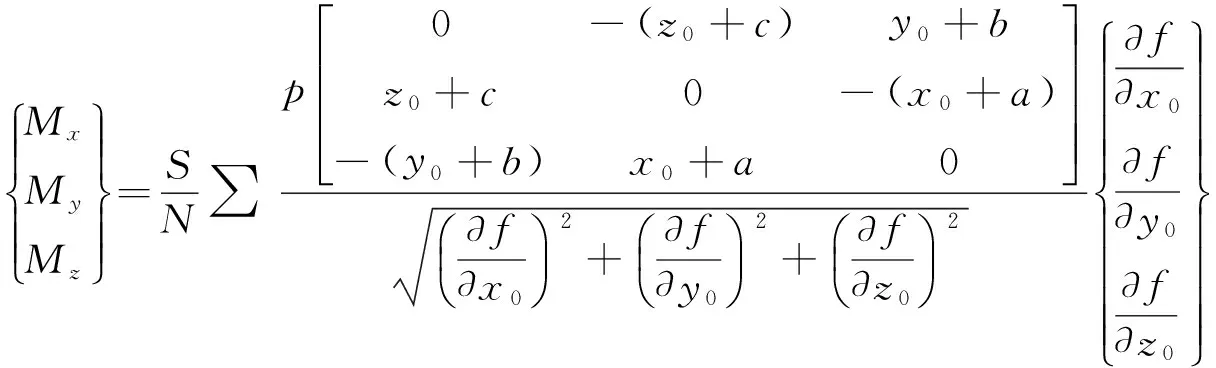
对Z轴倾覆力矩表示为

(6)

动不平衡量表示为

(7)

3.3风阻与转速的关系

图 7给出了辐射计受到的风阻合力、风阻合力矩、对Z轴倾覆力矩及动不平衡量随转速的变化曲线。由曲线可知，风阻合力中的Y轴分量和Z轴分量与转速成平方关系，而X轴分量相对较小；风阻合力矩与转速成平方关系，且X轴分量要大于Y轴分量；对Z轴倾覆力矩与转速也成平方关系，而动不平衡量则对转速不敏感。

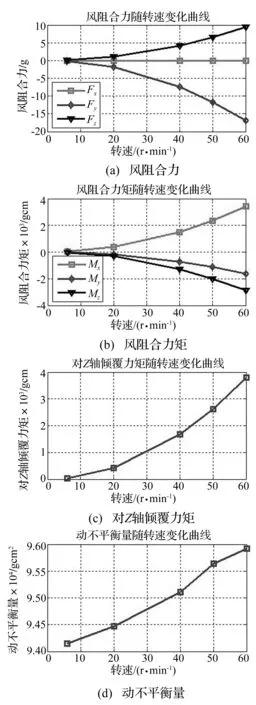
图7　风阻合力、合力矩、对Z轴倾覆力矩和动不平衡量随转速变化曲线Fig.7 The impacts of rotate velocity to resultant force, resultant moment, overturning moment to Z axis and dynamic unbalance

3.4风阻与环境气压的关系

图 8给出了微波辐射器受到的风阻合力、风阻合力矩、对Z轴倾覆力矩及动不平衡量随环境气压的变化曲线。由曲线可知，随着环境气压的降低，风阻合力、风阻合力矩、对Z轴倾覆弯矩及动不平衡量均以线性关系下降。特别需要指出的是，当环境气压下降至0.01个大气压时，风阻产生的对Z轴的倾覆弯矩仅为标准大气压下的2%，可以忽略不计。

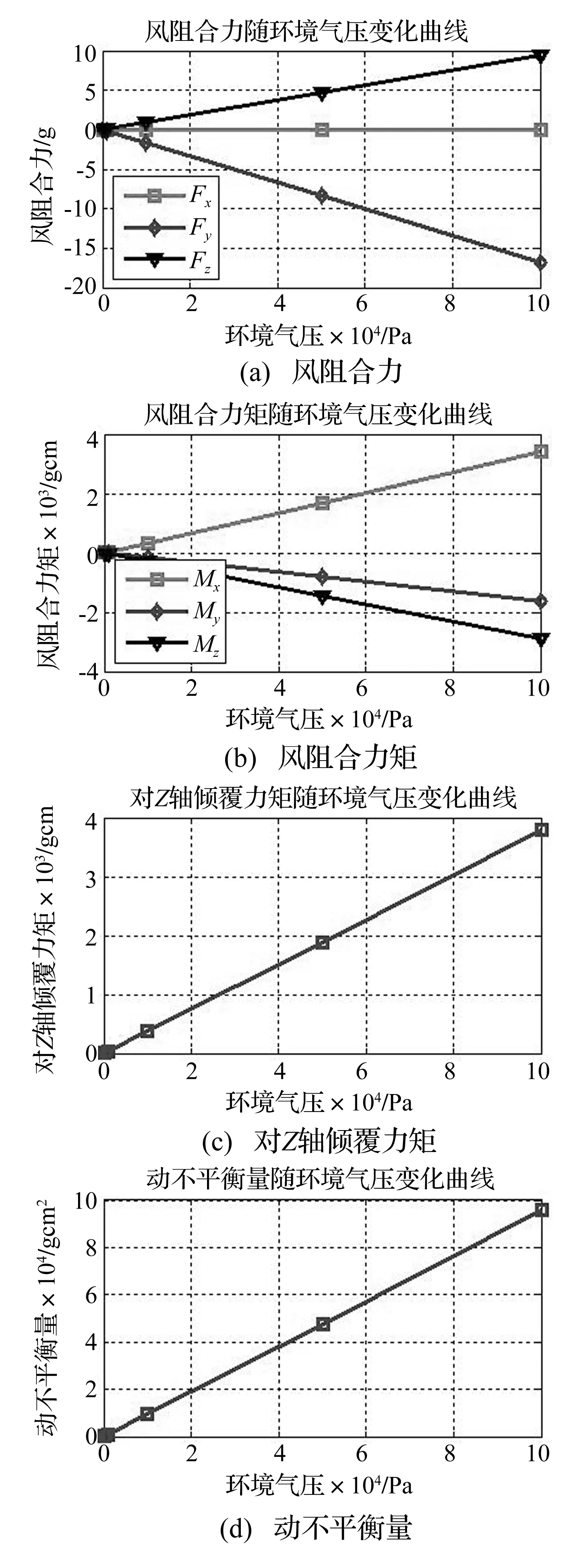
图8　风阻合力、合力矩、对Z轴倾覆力矩和动不平衡量随环境气压变化曲线Fig.8 The impacts of environment air pressure to resultant force, resultant moment,overturning moment to Z axis and dynamic unbalance

4空间环境对动平衡的影响

微波辐射计的工作环境为空间环境，而动平衡配平及测试环境为地面环境，对比空间环境和地面测试环境，除大气环境外，还需要考虑如下因素的影响：重力因素、在轨热变形、在轨无重力下轴承径向游隙变化。

4.1重力因素影响分析

静不平衡量的数学表示为：

S=me

(8)

式中，m为质量，单位g，e为质心偏离旋转轴线位置，单位cm或mm。由式(8) 可知，静不平衡量与重力无关。

静平衡测试原理是利用待测对象重力作用在若干个称重传感器上，通过称重力传感器的测重结果计算质心位置，G=mg，m为质量，g为重力加速度，重力加速度在每个称重传感器上的值相同且为定值，因此重力不影响静平衡测试结果。

动不平衡量的数学表示为：

D=m1r1h1+m2r2h2=mrh

(9)

式中，m1r1为上配平平面剩余质量与配平半径的矢量积；m2r2为下配平平面剩余质量与配平半径的矢量积；h1为上配平平面距安装面的高度；h2为下配平平面距安装面的高度。由式9可知，动不平衡量与重力无关。

动平衡测试时辐射计转轴竖直向上，和重力方向平行，辐射计在重力的影响下会产生轴向弹性变形，而在轨失重环境下，弹性变形回复，引起测试状态与在轨状态轴向高度的细微变化，因此，重力影响动平衡测试结果。

动不平衡量变化值可以通过弹性变形量占总高度的比例来计算，具体表示为：

ΔD=DΔh/h

(10)

4.2热变形影响分析

辐射计在轨受温度场影响会产生径向热变形Δr和轴向热变形Δh。由于静不平衡量表示转动部分质量和质心偏离轴线的距离的乘积，轴向热变形不影响静不平衡量。动不平衡量中包含轴向高度信息，因此轴向热变形对动不平衡量有影响。径向热变形同时影响静不平衡量和动不平衡量。

在ΔT的温度变化量下辐射计的热变形表示为

Δr=rαΔTΔh=hαΔT

(11)

静不平衡量变化值为：

ΔS=mΔr

(12)

动不平衡量变化值为：

(13)

4.3轴承径向游隙变化影响分析

在地面进行静平衡与动平衡测试时，转子轴承在重力作用下中心自定位，使得地面测试状态没有包含轴承径向游隙Δb。在轨工作时，由于辐射计头部处于失重状态，轴承径向游隙会使得转动轴线偏向一侧，导致式(8)和式(9)中的半径r产生了Δb的变化量，则

静不平衡量变化值为：

ΔS=mΔb

(14)

动不平衡量变化值为：

ΔD=DΔb/r

(15)

最终，重力因素、在轨热变形和轴承径向游隙变化对辐射计静不平衡量和动不平衡量测试结果的影响汇总如表1所示。对静不平衡量测试结果影响最大的是轴承径向游隙变化，而动不平衡量测试结果的差异主要来自于重力因素。由于上述两个因素在进行地面测试时是无法消除的，因此在进行辐射计的动平衡配平时需要考虑到这种差异的存在，预留一定的变化余量。

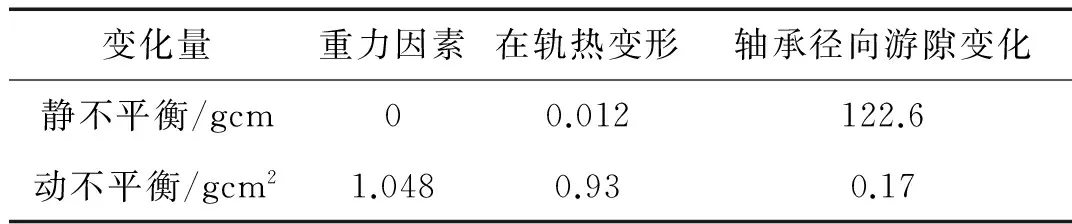
表1　空间环境对动不平衡量的影响

5微波辐射计的动平衡试验

在型号研制过程中，开展了针对微波辐射计的动平衡试验，动平衡试验在低气压罐中进行，当真空度达到要求时，进行动平衡测试与配平工作，最终微波辐射计的静不平衡量和动不平衡量达到设计指标要求。海洋二号卫星于2011年8月6日成功发射，卫星入轨后，微波辐射计开机工作，最终在载荷旋转扫描状态下，海洋二号卫星三轴姿态指向精度优于0.01°，姿态稳定度优于0.001°。图 9为微波辐射计开机状态下，海洋二号卫星绕滚动轴、俯仰轴、偏航轴的角速度在轨测量曲线。

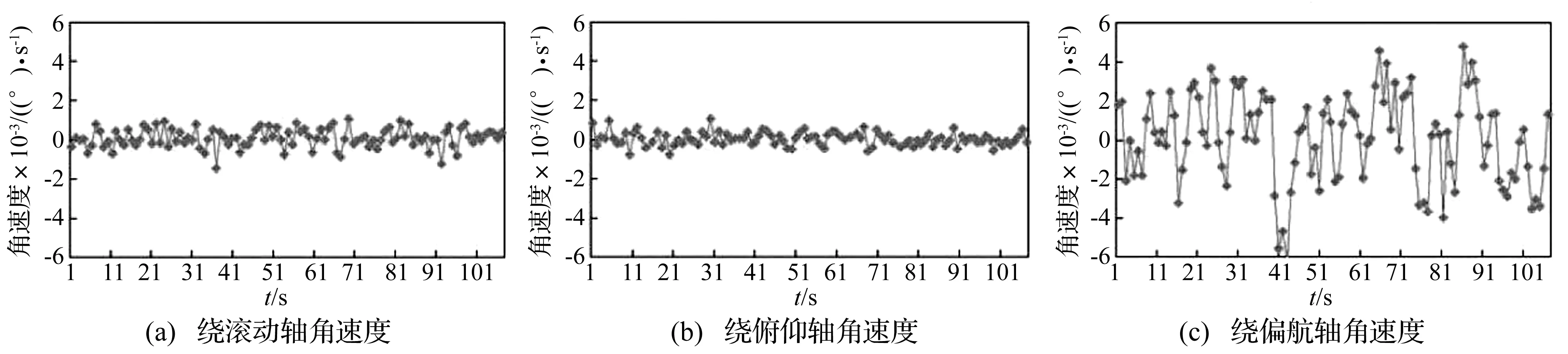
图9　卫星绕滚动轴、俯仰轴、偏航轴角速度在轨曲线Fig.9 Satellite angular velocity about rolling, pitching and yawing axis

6结论

以微波辐射计为代表的大型回转载荷的静不平衡量和动不平衡量，极大影响了卫星的高精度姿态控制能力。结合海洋二号卫星型号研制需求，开展了针对大型回转载荷的动平衡设计仿真与试验，通过相对较小的配重质量增加，极大改善了产品的动平衡特性，达到了设计指标要求。通过海洋二号卫星微波辐射计的动平衡设计仿真与试验，摸索出了一套解决星载大型回转载荷动不平衡问题的方法，为后续多颗气象海洋卫星大型回转载荷的研制积累了宝贵经验。

参 考 文 献

[1] 刘军,韩潮,张伟. 星上转动部件对卫星姿态的影响分析及补偿控制[J]. 上海航天,2006(6):22-26.

LIU Jun,HAN Chao,ZHANG Wei. Analysis on disturbance of mobile bodies and compensation control of satellite attitude[J]. Aerospace Shanghai,2006(6):22-26.

[2] 李延明,姜敏,余锐,等. 海洋二号卫星微波辐射计系统设计[J]. 中国工程科学,2013,15(7):39-43.

LI Yan-ming,JIANG Min,YU Rui,et al. System design of microwave radiometer of HY-2A satellite[J]. Engineering Science,2013,15(7):39-43.

[3] 蒋兴伟,林明森,宋清涛. 海洋二号卫星主被动微波遥感探测技术研究[J]. 中国工程科学,2013,15(7):2-11.

JIANG Xing-wei,LIN Ming-sen,SONG Qing-tao. Active and passive microwave remote sensing technology of the HY-2A ocean satellite mission[J]. Engineering Science,2013,15(7):2-11.

[4] 孟光. 转子动力学研究的回顾与展望[J]. 振动工程学报,2002,15(1):1-9.

MENG Guang. Retrospect and prospect to the research on rotordynamics[J]. Journal of Vibration Engineering,2002,15(1):1-9.

[5] 杜晨. 卫星动不平衡方法研究[J]. 航天器环境工程,2005,22(3):147-149.

DU Chen. Study on satellite unbalance method[J]. Spacecraft Environment Engineering,2005,22(3):147-149.

[6] Donald L K,Mark C N. A generalized dynamic balancing procedure for the AH-64 tail rotor[J]. Journal of Sound and Vibration,2009,326:353-366.

[7] Vincent G.V,An applicational process for dynamic balancing of turbomachinery shafting[R]. NASA Technical Memorandum 102537,1990.

[8] Nguyen V K,Nguyen P D. Balancing conditions of spatial mechanisms[J]. Mechanism and Machine Theory,2007(42):1141-1152.

[9] Van Der Wijk V,Demeulenaere B,Gosselin C,et al. Comparative analysis for low-mass and low-inertia dynamic balancing of mechanisms[J]. Journal of Mechanisms and Robotics,2012(4):1-8.

[10] Alici G,Shirinzadeh B. Optimum dynamic balancing of planar parallel manipulators based on sensitivity analysis[J]. Mechanism and Machine Theory,2006(41):1520-1532.

[11] Ayari L,Kubitschek M,Ashton G,et al. GMI instrument spin balance method,optimization,calibration,and test[R]. Proceedings of the 42nd Aerospace Mechanisms Symposium,2014.

[12] 朱晓农. 旋转机械的平衡[M]. 北京:机械工业出版社,1998．

[13] 王朋朋,牛宝华,艾永强. 星载大型不规则回转体的动平衡设计仿真[J]. 空间电子技术,2013(2):68-74.

WANG Peng-peng,NIU Bao-hua,AI Yong-qiang. Dynamic balancing design and simulation of large on satellite unbalanced rotating body[J]. Space Electronic Technology,2013(2):68-74.

Dynamic balancing design simulation and test for HY-2A satellite microwave radiometer

WANG Peng-peng1, NIU Bao-hua1, AI Yong-qiang1, WANG San-min2

(1. China Academy of Space Technology (Xi’an), Xi’an 710100, China; 2. School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an 710072, China)

Abstract:In order to realize high precision attitude control of a satellite, the dynamic balancing design simulation and test for large rotating payload of microwave radiometer should be conducted. Combining with the research and development of HY-2A satellite, the dynamic balancing design and simulation of its microwave radiometer was performed to provide the basis for its structural optimization and layout design. The effects of air resistant force on the radiometer’s dynamic balancing were analyzed. The influences of gravity, thermal expansion and variation of bearing radial clearance on the radiometer’s dynamic balancing were also considered. Finally, the radiometer’s dynamic balancing test was performed in vacuum environment and its dynamic balance target was achieved with very small added weights.

Key words:microwave radiometer; large rotating payload; dynamic balancing

收稿日期：2014-11-21修改稿收到日期：2015-05-12

中图分类号:V474.2

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.001

第一作者 王朋朋 男，硕士，工程师，1985年9月生