半圆盘构件冲击断裂特性的动态焦散线实验研究

李　清， 郭　洋， 马万权， 王梦远， 韩　通

(中国矿业大学 (北京)力学与建筑工程学院，北京　100083)

半圆盘构件冲击断裂特性的动态焦散线实验研究

李清， 郭洋， 马万权， 王梦远， 韩通

(中国矿业大学 (北京)力学与建筑工程学院，北京100083)

摘要：采用动态焦散线实验系统，对有机玻璃(PMMA)在冲击载荷下的Ⅰ型和Ⅰ-Ⅱ混合型裂纹在起裂和扩展时的动态断裂特性进行了研究。结果表明：随着PMMA由Ⅰ型断裂转变为Ⅰ-Ⅱ混合型断裂，从落锤作用在试件上到裂纹起裂所需时间不断增加，说明裂纹起裂需要的能量有所增加，同时从裂纹起裂到最终贯通所需时间不断减少，说明裂纹平均扩展速度也不断增大；在Ⅰ型断裂中，PMMA的断裂韧度KⅠC为2.04 MN/m3/2，而在Ⅰ-Ⅱ混合型断裂中，PMMA的断裂韧度KⅠC低于Ⅰ型断裂时的断裂韧度KⅠC，但是KⅡC有所增大；对于Ⅰ-Ⅱ混合型断裂，PMMA极限扩展速度约为366 m/s，当达到极限扩展速度后，裂纹尖端出现微裂纹增韧现象，使裂纹的表面能迅速增大，随后裂纹的扩展速度迅速减小。

关键词：冲击断裂；动态焦散线；断裂韧度；半圆盘构件；预制裂纹

有机玻璃(PMMA)作为一种高透光率、易加工、高强度且低价格的材料，已广泛用于建筑装饰、工艺品、航空玻璃、仪器部件等各个方面。然而，由于有机玻璃在常温下表现为一种准脆性材料，在使用过程中，往往因受到不同载荷的作用而产生裂纹，出现破坏，危及使用人员的安全，并造成大量的经济损失。因此，一些学者针对有机玻璃在不同情况下的断裂特性进行了广泛的研究。肖健[1]研究了正弦交变载荷对航空用有机玻璃材料疲劳裂纹扩展的影响。荣吉利等[2]对航空有机玻璃进行研究，得到了其动态力学参数。吴国夫[3]对有机玻璃在蠕变过程中的银纹扩展和损伤问题进行了研究，并提出了采用双曲线函数描述银纹损伤密度变化规律。王泓[4]将金属材料疲劳断裂中的静态断裂模式引入到有机玻璃裂纹扩展的研究中，建立了有机玻璃疲劳裂纹扩展速率和应力强度因子与弹性模量、门槛值(材料发生断裂所需的最小应力值)和断裂韧性之间的关系式。吴衡毅等[5]采用MTS试验机和自行研制的设备进行了有机玻璃单向拉伸实验，研究表明，在中、低应变率下，有机玻璃表现出较强的应变率强化、应变率硬化和高速脆性的力学性质。周君等[6]采用中心切口圆盘试件研究了有机玻璃的纯Ⅰ型和纯Ⅱ型动态断裂行为，结果表明，有机玻璃的纯Ⅰ型和纯Ⅱ型断裂韧度随加载速率的增大而显著增大。Chen等[7]采用分离式霍普金森杆对有机玻璃进行了不同应变率下的动态拉伸和压缩实验。发现在动态拉伸实验中，有机玻璃的破坏应变低于静态实验值，而在动态压缩实验中，有机玻璃的动态压缩强度明显高于静态压缩强度值。Huang等[8]采用SHPB对有机玻璃的动态断裂特性进行了研究，发现有机玻璃的起裂韧度和扩展时的断裂韧度均随加载率的提高而提高，并建立了裂纹扩展速度和动态应力强度因子之间的关系。这些学者采用不同的研究手段对有机玻璃在疲劳荷载、静态荷载、动态荷载等多种工况下的力学行为进行了研究，揭示了裂纹的断裂形态与扩展速度、断裂韧度与加载速率之间的规律。然而，对于有机玻璃在动载作用下裂纹的起裂和扩展这一动态过程的研究相对较少，尤其是裂纹的起裂对构件的破坏相当重要。但由于这一过程持续时间极短，裂纹尖端不易确定，这就给裂纹起裂和扩展规律的研究带来了困难。焦散线实验方法是一种非接触式的光测力学方法，其对裂纹尖端的局部应力梯度十分敏感，能够准确地判断裂纹尖端的位置，且能够定量分析裂纹尖端的动态应力强度因子，在研究裂纹的起裂、扩展及动态应力强度因子等材料的动态断裂特性方面具有较大的优势[9]。因此，本文采用动态焦散线实验方法结合高速数字相机，对有机玻璃在冲击载荷下裂纹的起裂、扩展行为及动态应力强度因子的变化规律进行了研究。

1实验测试原理

1.1焦散线的形成原理

焦散线方法是考虑到固体中的应力发生变化时，其光学性质也随之发生变化。图1表示了焦散线的形成原理。一个厚度为d的试件在载荷σ0的作用下，试件因受力变形产生裂纹，由于裂纹尖端附近的应力梯度极大，试件的厚度和折射率就会相应改变，离裂纹尖端越近的区域其变化也就越大。因此，平行光场入射到这一区域，透射时将不再垂直于试件表面，光线发生偏转，在距试件Z0处的参考平面上，就会观察到一个暗斑，即焦散斑。包围焦散斑的亮线就是焦散线。由于焦散斑的形状随裂纹受力情况的不同而变化，因此，可以根据焦散斑的形状，判断裂纹的受力特点。图2分别表示了Ⅰ型和Ⅱ型裂纹尖端焦散斑的形状。

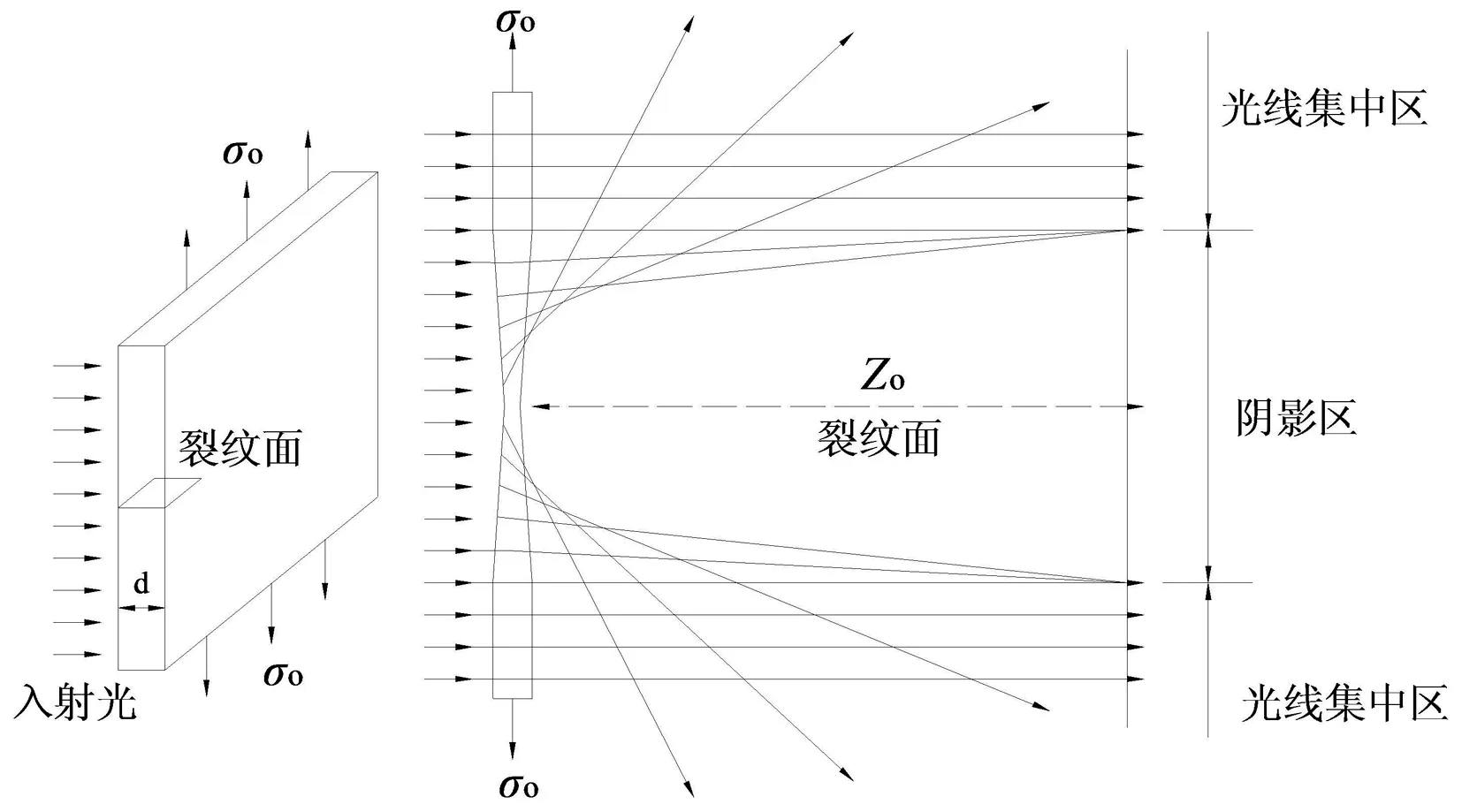
图1　焦散线成像示意图Fig.1 Schematic diagram of caustic formation

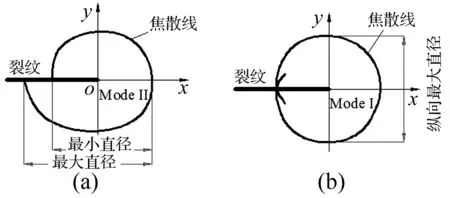
图2　Ⅰ型和Ⅱ型裂纹尖端焦散斑形状Fig.2 Caustics shape at crack tip under Mode Ⅰ/ Mode Ⅱ

1.2动态应力强度因子的测定

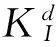
(1)

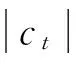
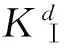
(2)

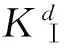
(3)

式中，Dmax为焦散斑最大直径，Dmin为焦散斑最小直径，如图2(b)所示，文献[9]给出了μ与(Dmax-Dmin)/Dmax之间的关系曲线，以及g与μ之间的关系曲线，通过测量裂纹尖端焦散斑的特征尺寸(Dmax,Dmin)，可根据(Dmax-Dmin)/Dmax与μ的关系曲线确定μ值，再通过μ与g的关系曲线，可得到相应的g值。其它参数与式(1)相同。

2试件制备与数字激光动态焦散线实验系统

2.1NSCB试件制备

由于预制裂纹半圆盘三点弯曲 (Notched Semi-Circular Bending, NSCB)实验试件制作简单方便，很多学者将其作为研究脆性材料动态断裂特性的标准试件[13-16]。本文采用三点弯曲落锤冲击实验，图3为实验模型试件示意图。试件的半径R=50 mm，厚度d=5 mm，预制裂纹的长度满足a/2R=0.15，预制裂纹宽度为0.6 mm，裂尖宽度为0.3 mm。预制裂纹的方向与落锤加载方向的夹角θ分别为0°、15°和30°。支座间距S满足S/2R=0.43。有机玻璃试件的动态力学参数如表1所示。

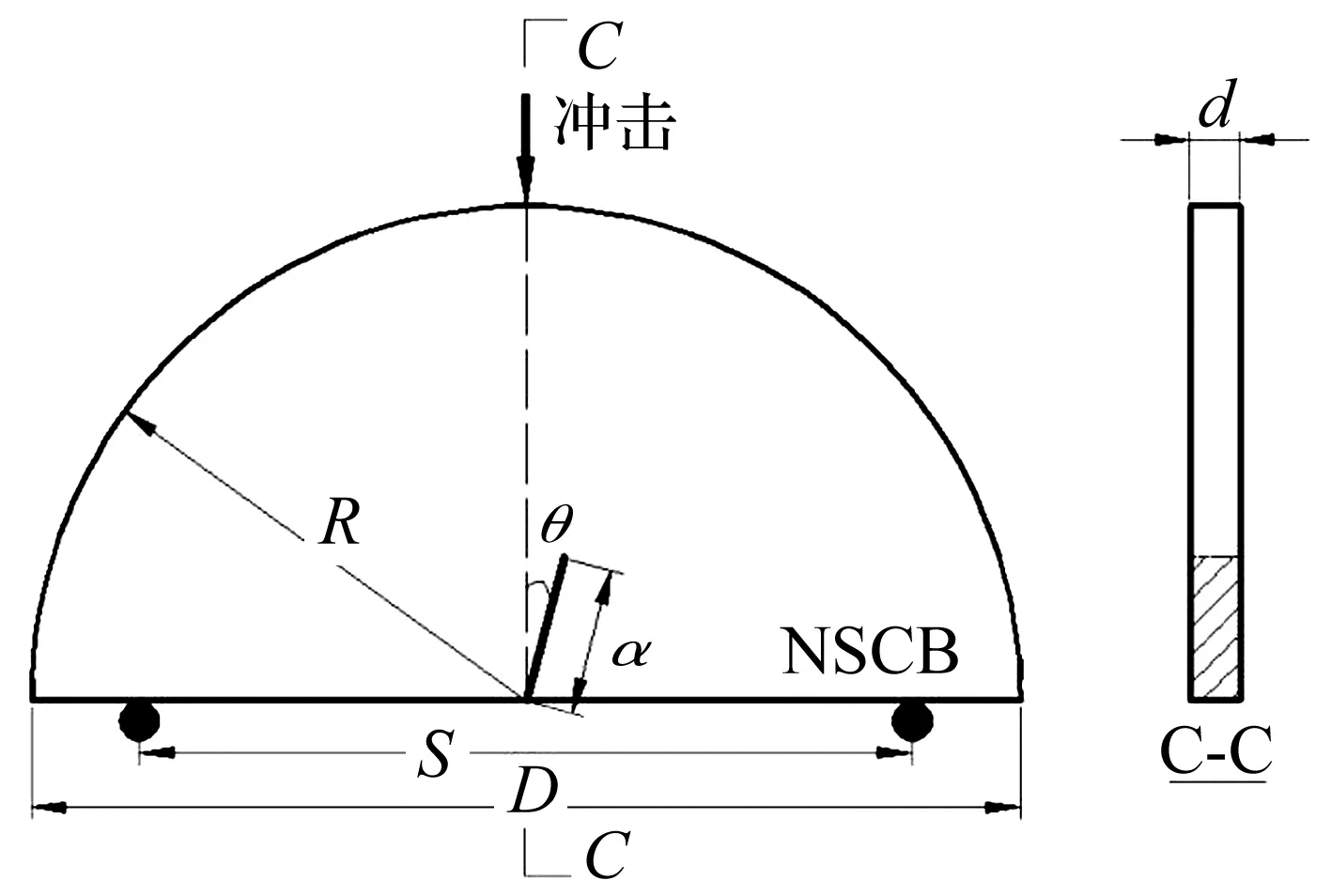
图3　实验模型试件示意图Fig.3 Schematic diagram of experimental specimen models

参数Cp/(m·s-1)CS/(m·s-1)Ed/GPaυct/(m2·N-1)数值232012606.10.310.88×10-10

注：CP表示膨胀波传播速度，Cs表示剪切波传播速度，Ed表示动态弹性模量，υ表示动态泊松比,ct表示材料的光学应力常数。

为了在试件上预制尖锐的裂纹尖端，保证实验结果的可靠性。本文分两步制作预制裂纹裂尖，第一步，采用激光从半圆盘试件的圆心处按预设的裂纹角度，略小于预设的长度进行切割，形成表面平整的预制裂纹；第二步，采用厚度为0.3 mm的锯齿沿预制裂纹的方向切割预制裂纹末端，从而在预制裂纹末端形成一个尖锐的裂尖。

2.2实验光路及设备

图4为实验光路示意图。实验采用透射式焦散线实验系统，利用落锤自由下落对试件进行冲击加载。落锤质量为0.82 kg，落锤下落高度为321 mm。实验时严格保证落锤每次下落的高度相同。高速相机为美国生产的Fastcam-SA5(16G)型彩色高速数码相机，最大拍摄速度为1 000 000 fps，能够满足超动态测试要求。实验采用绿色激光光源，其波长位于数码相机的最敏感光波波长范围内。实验时，根据不同实验需求，光强在0～200 mW范围内可调。综合考虑，本次实验相机拍摄速度为3×105fps，拍摄照片的分辨率为256×64 pixels，光强为60 mW。

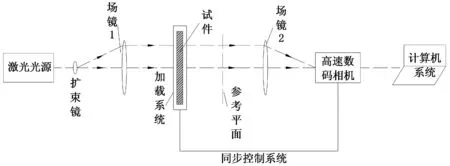
图4　实验光路示意图Fig.4 Schematic diagram of experimental optical system

3实验结果及分析

3.1焦散线图像与断裂模式分析

图5表示预制裂纹半圆盘试件断裂效果图。图6、图7和图8分别表示预制裂纹的角度为0°、15°和30°时半圆盘试件的焦散斑系列图片。图中t=0 μs时刻表示落锤恰好击中试件的上边缘，应力波开始由冲击点向下传播。

图5　预制裂纹半圆盘试件断裂效果图Fig.5 Fracture patterns of NSCB samples

0.00μs　　20.00μs　　46.67μs　　73.33μs　　100.00μs　126.67μs　　153.33μs　180.00μs　206.61μs　　240.00μs

286.67μs　333.33μs　　380.00μs 　426.67μs　473.33μs　　52.00μs　566.67μs　　613.33μs　66.00μs　　700.00μs图6　0°预制裂纹半圆盘试件焦散斑系列图片Fig.6 Caustics photographs of NSCB specimen with crack angle θ=0°

0.00 μs　60.00μs　　100.00μs　120.00μs　　160.00μs　180.00μs　　220.00μs　253.33μs　280.00μs　　300.00μs

340.00μs　360.00μs　　400.00μs　420.00μs　460.00μs　　480.00μs　520.00μs　　540.00μs　580.00μs　　660.00μs图7　15°预制裂纹半圆盘试件焦散斑系列图片Fig.7 Caustics photographs of NSCB specimen with crack angle θ=15°

0.00 μs　60.00 μs　　133.33μs　320.00μs　　446.67μs　566.67μs　　586.67μs　606.67μs　　626.67μs　646.67μs

666.67μs　686.67μs　　706.67μs　726.67μs　　746.67μs　766.67μs　　786.67μs　806.67μs　　 826.67μs　846.67μs图8　30°预制裂纹半圆盘试件焦散斑系列图片Fig.8 Caustics photographs of NSCB specimen with crack angle θ=30°

应力波迅速传播并作用在预制裂纹尖端上，预制裂纹尖端开始出现焦散斑，其大小和形状随应力波在试件内部的反射叠加而不断变化，呈先增大后减小，又再次增大直至裂纹起裂，并快速从预制裂纹尖端向落锤冲击点扩展的规律。当预制裂纹角度为0°时，如图6所示，预制裂纹尖端处的焦散斑呈近似圆形，为Ⅰ型焦散斑。当t=240 μs时，裂纹起裂，并沿预制裂纹方向迅速失稳扩展，当t=406.67 μs时，裂纹扩展出现停滞现象，持续46.67 μs后又再次向落锤冲击点方向扩展，直到试件完全贯通。当预制裂纹角度增大到15°时，如图7所示，预制裂纹尖端处的焦散斑呈 “鸭蛋状”，为Ⅰ-Ⅱ混合型焦散斑。当t=253.33 μs时，裂纹起裂，并偏离预制裂纹方向扩展，与预制裂纹角度为0°时情况相比起裂时间延迟了13.33 μs，随后裂纹快速扩展至落锤冲击点。当预制裂纹角度进一步增大到30°时，如图8所示，在裂纹起裂前，其尖端处焦散斑大小振荡变化的时间进一步增加，直到t=600 μs时预制裂纹才开始起裂。当t=653.33 μs时，在裂纹尖端焦散斑的尾部出现一个新的焦散斑，裂纹尖端出现了微裂纹，分散了主裂纹尖端的能量，使裂纹的扩展速度迅速下降直至停滞。从能量守恒的角度来看，这是因为当裂纹的扩展速度增大到一定值时，即裂纹扩展释放的弹性应变能超过了新裂纹表面所需要的表面能和裂纹尖端材料塑性变形所需要的功之和，裂纹尖端区域的高能量诱发相变导致在尖端产生微裂纹，增加了裂纹表面的粗糙度，提高了表面的断裂能，因此，裂纹的扩展速度随之迅速下降。此后，由于主裂纹尖端应力场的影响，当t=713.33 μs时，微裂纹与主裂纹汇合，主裂纹尖端的应力强度因子再次增大，主裂纹的速度再次增大，并快速向落锤冲击点扩展。

图9表示从落锤作用在试件上到预制裂纹起裂以及预制裂纹从起裂到最终贯通所需时间随预制裂纹角度的变化曲线。随着预制裂纹角度的增加，裂纹起裂所需时间不断增加，而预制裂纹从起裂到最终贯通所需时间则不断减少。这是因为随着预制裂纹角度的增加，裂纹尖端的应力场由拉伸应力场逐渐转变为拉剪应力场，预制裂纹尖端的起裂也由Ⅰ型模式转化为Ⅰ-Ⅱ混合型模式，从实验后的图片中可以看出，裂纹起裂后的曲裂程度也不断增加。需要消耗的能量也就增多，因此起裂前需要更多的时间来积聚能量。而在预制裂纹起裂后，由于预制裂纹角度增大，预制裂纹尖端在起裂前储存的能量不断增多，使裂纹扩展后的动能大大增加，裂纹的扩展速度也相应增大，因此，裂纹全部贯通需要的时间也不断减少。需要注意的是，由于裂纹的扩展速度存在极限值，一般为0.3倍～0.7倍的材料瑞利波波速，因此，裂纹贯通需要的时间不会一直下降，最终会趋于一个稳定值。

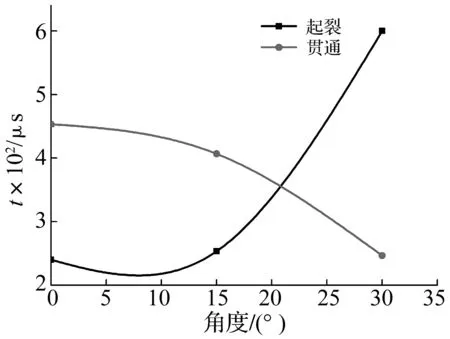
图9　不同角度的裂纹起裂和贯通的时间变化曲线Fig. 9 Crack initiation and transfixion vs. time of different angle

3.2动态应力强度因子的变化

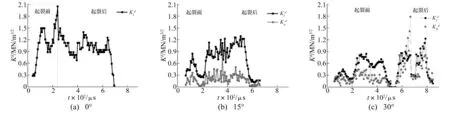
图10　动态应力强度因子和随时间的变化曲线Fig.10 Dynamic stress intensity factor and vs. time

3.3主裂纹扩展速度的变化

图11为冲击载荷作用下不同角度预制裂纹扩展速度随时间变化曲线。当预制裂纹的角度为0°时，预制裂纹在起裂后，扩展速度迅速上升并达到最大值260 m/s，随后逐渐振荡下降，在裂纹扩展到距落锤冲击点7.93 mm处(约为试件总高度的1/6)，受冲击力的影响，裂纹的扩展速度出现小幅度上升后又振荡下降。当预制裂纹的角度增加到15°时，预制裂纹的扩展速度也迅速上升并达到最大值265 m/s，然后缓慢下降，并在t=440 μs时速度基本下降到最低点，仅为9.18 m/s，此时裂纹扩展到距落锤作用点5.29 mm处，随后，裂纹扩展速度再次小幅度上升，随后振荡下降直至贯通。当预制裂纹的角度为30°时，预制裂纹在t=600 μs时才起裂，由于此时预制裂纹尖端附近区域储存的能量较大，裂纹扩展速度迅速增大，在起裂后53 μs时达到最大值366 m/s，随后裂纹扩展速度迅速下降。结合图8可知，这是因为裂纹扩展速度太快而在尖端出现微裂纹增韧现象，增加了裂纹表面的粗糙度，使裂纹扩展速度迅速下降。当微裂纹与主裂纹汇聚后，裂纹扩展速度再次上升，随后振荡下降直至全部贯通。

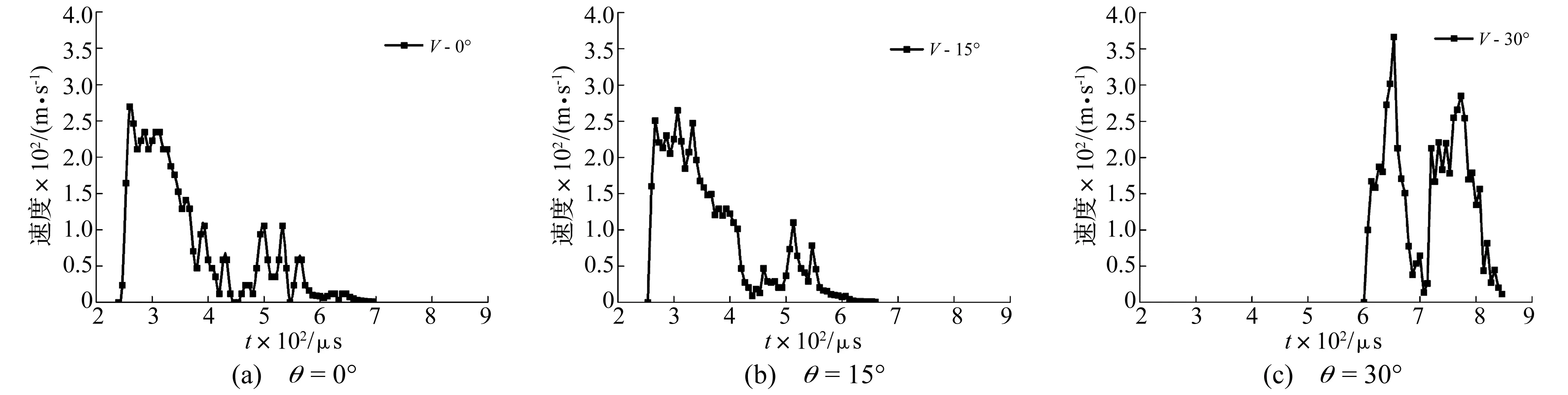
图11　不同角度预制裂纹扩展速度随时间变化曲线Fig.11 Pre-crack propagation velocity vs. time of different angles

随着预制裂纹角度的增加，裂纹的平均扩展速度不断增大。当预制裂纹的角度分别为0°、15°和30°时，裂纹的平均扩展速度分别为77.24 m/s、89.45 m/s和161.58 m/s。扩展速度越大，增韧现象越明显，表面能越大，裂纹断裂需要的能量也就越多，因此，起裂前能量积累的时间也就越长。这与实验中观察到的裂纹起裂时间随预制裂纹角度的增加而不断增加的现象相一致。

4结论

(1) 随着预制裂纹角度的增加，PMMA的断裂模式逐渐由Ⅰ型转变为Ⅰ-Ⅱ混合型，裂纹扩展的曲裂程度增加。

(2) PMMA断裂模式由Ⅰ型转变为Ⅰ-Ⅱ混合型后，裂纹起裂时需要的能量有所增加，裂纹起裂所需时间不断增加，从裂纹起裂到最终贯通所需时长不断减少。

(3) 在Ⅰ型断裂中，PMMA的断裂韧度KIC为2.04 MN/m3/2，而在Ⅰ-Ⅱ混合断裂中，PMMA的断裂韧度KⅠC低于Ⅰ型断裂韧度，Ⅱ型断裂韧度KⅡC有所增大。在起裂前，裂纹尖端的应力强度因子的波动现象反映了裂纹尖端区域的应力调整和重组的变化特征。

(4) 随着预制裂纹角度的增加，预制裂纹的平均扩展速度不断增大。在Ⅰ-Ⅱ混合断裂中，当裂纹的扩展速度达到极限扩展速度时，裂纹尖端出现微裂纹增韧现象，使裂纹的表面能迅速增大，随后裂纹的扩展速度迅速下降。

参 考 文 献

[1] 肖健. MDYB-3航空有机玻璃疲劳裂纹特性的试验研究[D].西安：西北工业大学,2004.

[2] 荣吉利，诸葛迅，李健，等.不同弹头形式的易碎弹冲击航空有机玻璃的数值分析[J]. 振动与冲击，2015,34(1):200-205.

RONG Ji-li,ZHU Ge-xun，LI Jian,et al. Numerical analysis on fragile projectile with different warheads impacting against aviation organic glass[J]. Journal of Vibration and Shock,2015,34(1):200-205.

[3] 吴国夫,朱西平,高宗战,等. 蠕变载荷下有机玻璃银纹萌生及损伤研究[J]. 航空材料学报,2012,32(3):79-84.

WU Guo-fu,ZHU Xi-ping,GAO Zong-zhan,et al. Experimental study on crazing initiation and damage in PMMA under creep[J]. Journal of Aeronautical Materials,2012,32(3):79-84.

[4] 王泓,鄢君辉,郑修麟. 有机玻璃疲劳裂纹扩展表达式及控制参量[J]. 航空学报,2001,22(1):83-86.

WANG Hong,YAN Jun-hui,ZHENG Xiu-lin. Formulae and governing parameters of fatigue crack propagation in polymethy imethacrylate[J]. Journal of Aeronautical Materials,2001,22(1):83-86.

[5] 吴衡毅,马钢,夏源明. PMMA低、中应变率单向拉伸力学性能的实验研究[J]. 实验力学,2005,20(2):193-199.

WU Heng-yi,MA Gang,XIA Yuan-ming. Experimental study on mechanical properties of PMMA under unidirectional tensile at low and intermediate strain rates[J]. Journal of Experimental Mechanics,2005,20(2):193-199.

[6] 周君,汪洋,夏源明. 有机玻璃纯Ⅰ型和纯Ⅱ型动态断裂行为的实验研究[J]. 高分子材料科学与工程,2008,24(2):10-13.

ZHOU Jun,WANG Yang,XIA Yuan-ming. Experimental study of dynamic fracture behavior of PMMA under pure mode-Ⅰ and pure mode-Ⅱ loading conditions[J]. Polymer Materials Science and Engineering,2008,24(2):10-13.

[7] Chen W,Lu F,Cheng M. Tension and compression tests of two polymers under quasi-static and dynamic loading[J]. Polymer Testing,2002,21(2):113-121.

[8] Huang S,Luo S N,Tatone B S A,et al. Dynamic fracture tests of polymethylmethacrylate μsing a semicircular bend technique[J]. Journal of Mechanics of Materials and Structures,2011,6(6):813-826.

[9] Kalthoff J F. The shadow optical method of caμstics[M].Static and Dynamic Photoelasticity and Caμstics. Springer Vienna,1987:407-522.

[10] Beinert J,Kalthoff J F. Experimental determination of dynamic stress intensity factors by shadow patterns[M]. Springer Netherlands,1981:281-330.

[11] Rosakis A J. Analysis of the optical method of caustics for dynamic crack propagation[J]. Engineering Fracture Mechanics,1980,13(2):331-347.

[12] Papadopoulos G A. The experimental method ofcaustics and the Det.-Criterion of fracture [M]. London:Springer-Verlag,1993.

[13] Chong K P,Kuruppu M D. New specimen for fracture toughness determination for rock and other materials[J]. International Journal of Fracture,1984,26(2):59-62.

[14] Krans R L,Tolman F,Van de Ven M F C. Semi-circular bending test:a practical crack growth test μsing asphalt concrete cores [C]//Rilem Proceedings. Chapman & Hall,1996:123-132.

[15] Dai F,Chen R,Xia K. A semi-circular bend technique for determining dynamic fracture toughness[J]. Experimental Mechanics,2010,50(6):783-791.

[16] Xia K,Huang S,Dai F. Evaluation of the frictional effect in dynamic notched semi-circular bend tests[J]. International Journal of Rock Mechanics and Mining Sciences,2013 62:148-151.

[17] Van de Steen B,Vervoort A. Non-local stress approach to fracture initiation in laboratory experiments with a tensile stress gradient[J]. Mechanics of Materials,2001,33(12):729-740.

[18] Dong S,Xia K,Huang S,et al. Rate dependence of the tensile and flexural strengths of glass-ceramic Macor[J]. Journal of Materials Science,2011,46(2):394-399.

Dynamic caustics tests for semi-circular specimen under impact loading

LI Qing, GUO Yang, MA Wan-quan, WANG Meng-yuan, HAN Tong

(School of Mechanics & Civil Engineering, China University of Mining & Technology, Beijing 100083, China)

Abstract:The initiation and propagation of mode Ⅰ and mixed mode Ⅰ-Ⅱ cracks in Polymethylmethacrylate (PMMA) subjected to impact loading was studied by using a dynamic caustics test system. It was shown that the initiation from pure mode Ⅰ to mixed mode Ⅰ-Ⅱ needs more energy for PMMA, because the time needed for initiation increases. The time from crack initiation to crack arrest decreases, so the crack average propagation velocity increases; the fracture toughness KⅠCof PMMA is 2.04 MN/m3/2for mode Ⅰ fracture; for mixed mode Ⅰ-Ⅱ fracture, the fracture toughness KⅠCof PMMA is lower than that of mode Ⅰ fracture, but the fracture toughness KⅡCincreases; for mixed mode Ⅰ-Ⅱ fracture, the maximum propagation velocity of PMMA is about 366 m/s, then the micro-cracks toughening phenomenon appears at the crack tip, the surface energy of crack increases, and its propagation velocity decreases rapidly.

Key words:impact fracture; dynamic caustics; fracture toughness; notched semi-circular bending specimen; preexisted crack

基金项目：国家自然科学基金(51374212;51134025)

收稿日期：2015-06-10修改稿收到日期：2015-11-03

通信作者郭洋 女，博士，1989年生

中图分类号:TD2

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.009

第一作者 李清 男，博士，教授，1969年生

E-mail：kuangdaguoyang@sina.cn