双层超弹性铰链展开冲击分析与优化

杨　慧， 郭宏伟， 王　岩， 刘荣强， 陶建国

(哈尔滨工业大学 机电学院 机器人技术与系统国家实验室，哈尔滨　150080)

双层超弹性铰链展开冲击分析与优化

杨慧， 郭宏伟， 王岩， 刘荣强， 陶建国

(哈尔滨工业大学 机电学院 机器人技术与系统国家实验室，哈尔滨150080)

摘要：超弹性铰链依靠自身大挠度弹性折叠存储的弹性势能实现弹性展开，集驱动、旋转和锁定于一体。研究了双层超弹性铰链展开冲击性能，提出了降低双层超弹性铰链展开冲击优化方法。为了确保有限元模型的准确性，搭建实验平台对双层超弹性铰链进行动力学展开性能测试，基于实验结果对有限元模型进行修正。采用正交法试验设计建立展开冲击特性代理模型。以展开冲击角度和锁定时间最小为目标函数，采用改进的非支配遗传算法对双层超弹性铰链进行参数化优化设计，得到最优结构尺寸。对最优结构尺寸进行有限元展开分析，误差不大于5.008%，表明代理模型准确性。最优非等厚度与等厚度双层超弹性铰链对比，发现前者冲击角度和锁定时间分别降低52.154%和29.104%，优化后结构的冲击得到明显改善。通过参数研究发现，展开冲击对外侧带簧厚度较为敏感，锁定时间随带簧厚度增加表现出先减少后增大的趋势。

关键词：冲击；超弹性铰链；动力学分析；优化；星载天线

航天器受发射能力和体积的约束，如太阳能阵列、星载天线和固体反射器等受运载器有效载荷和承载能力的限制。超弹性铰链是一种薄壁圆柱壳体结构，类似于带弹簧(简称“带簧”)，依靠自身大挠度弹性变形实现折叠和弹性展开，集驱动、旋转和锁定于一体，不含移动部件、不存在摩擦，并具有轻质特点，能够解决航天器发射体积有效性问题。并且超弹性铰链能够有效降低星载可展开机构复杂度和发射成本，在航天领域具有极大的应用前景。近年来出现了一些自锁定带簧超弹性铰链形式[1]替代传统铰链，并成功应用于波音回弹反射器[2]和火星快速航天器[3]。

在航天器达到预定姿态时，通过释放约束使超弹性铰链驱动可展开机构展开。Seffen等[4]分别基于能量法和冲量-动量方程建立细长超弹性铰链可移动点铰链展开动力学模型，但未对展开之后超弹性铰链的冲击进行分析。Soykasap[5]对三缝圆管超弹性铰链的展开动力学性能进行分析，将展开过程分为展开、锁定过程和锁定三个阶段。如果动能过大超弹性铰链将发生屈曲并继续旋转，产生的振荡会对其它结构产生不利影响。Yao等[6]采用有限元方法对复合材料双缝圆管超弹性铰链展开过程中阻尼因素的影响进行了研究。Mallikarachchi等[7]通过实验研究了双缝圆管超弹性铰链展开过程的冲击，并对由两个纵向缝超弹性铰链构成1 m长轻质自展开圆杆进行展开动力学分析，通过实验验证杆轻质杆绕一个小型航天器两次折叠和展开过程中不会出现损坏。

本文研究的双层超弹性铰链由弹性金属合金构成，刚度较大，在展开末端时壳体突然翻转可能对可展开机构产生过冲，会对其他结构的稳定性产生影响。为了降低双层超弹性铰链展开末端冲击，研究了双层超弹性铰链动力学展开冲击性能，基于代理模型法提出了一种快速有效的降低双层超弹性铰链展开冲击的优化方法。搭建动力学展开实验平台对双层超弹性铰链进行展开性能测试，基于实验结果对有限元模型进行修正。由于双层超弹性铰链折叠和展开具有高度非线性，采用两因子五水平全因子正交法进行试验设计，借助于ABAQUS/Explicit软件进行数值仿真建立25组实验样本点，利用四次多项式建立表征双层超弹性铰链展开冲击特性的响应面数学模型。以展开冲击角度和锁定时间最小为目标函数，采用改进的非支配遗传算法对双层超弹性铰链进行参数化优化设计，得到最优结构尺寸。基于实验设计的样本点进行参数化研究，分析位于折叠外侧的两层带簧厚度对双层超弹性铰链展开冲击的影响。

1超弹性铰链大挠度折展特性

1.1静力学弯曲特性

超弹性铰链是一类沿纵向开缝薄壁圆柱壳体结构，依靠自身大挠度弹性变形存储弹性势能实现弹性展开，折叠和展开过冲中力矩具有高度非线性，如图1所示。定义带簧弯曲方向和横截面曲率方向相反时为背向弯曲，相同时为对向弯曲。图 1中实心箭头表示对向和背向弯曲折叠力矩路径，空心箭头表示相应的展开路径。带簧超弹性铰链对向折展时力矩路径相同，但是背向折展时的力矩路径不同，展开时的峰值力矩远小于折叠时的峰值力矩。

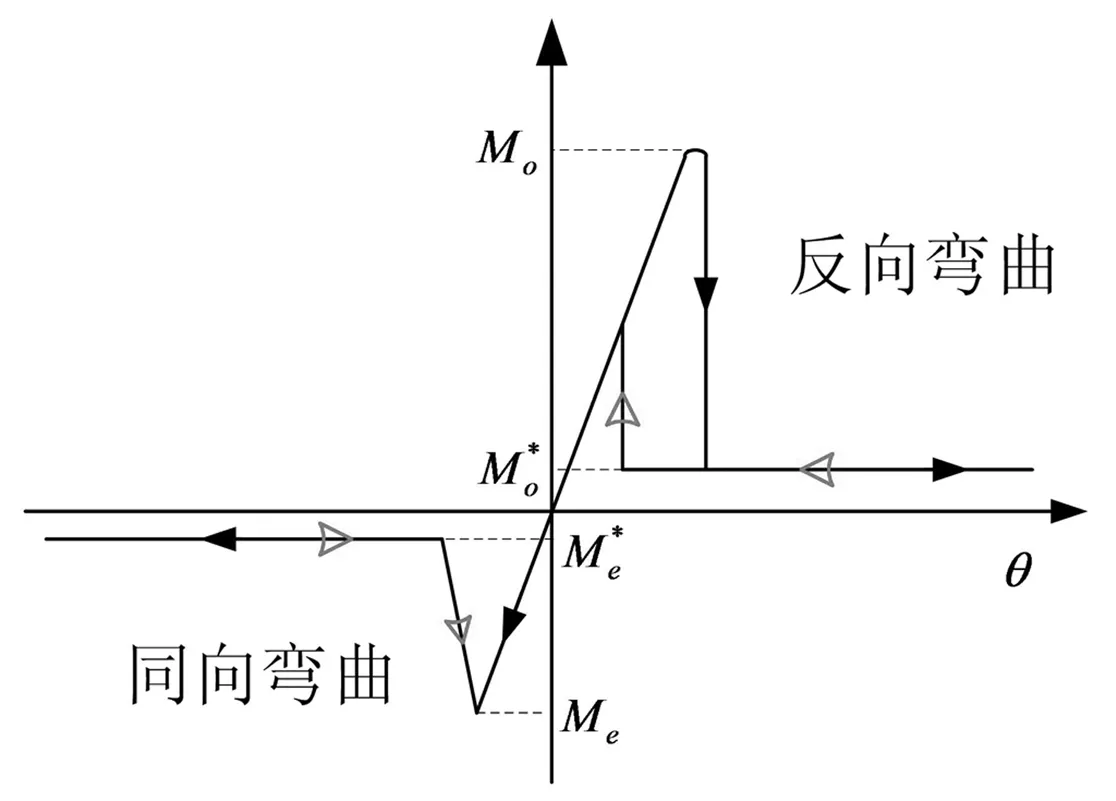
图1　带簧超弹性铰链背向和对向弯曲力矩曲线Fig.1 Moment curves for opposite and equal bend of tape-spring

1.2动力学展开特性

不同超弹性铰链在对向和背向折叠过程中力矩因结构屈曲出现峰值，随着折叠角度增加力矩趋于稳定，超弹性铰链动力学展开过程恢复曲线如图 2所示。展开时，角度随着时间增加而降低，该过程中力矩保持稳定。在展开接近平衡位置附近发生突然翻转，展开力矩出现峰值能够对整个机构具有锁定作用，超弹性铰链尝试锁定，在t0时刻实现锁定。但是当展开峰值力矩过大时，展开过程中会出现一定量冲击角θ，会对可展开机构中的其它部件产生影响。

图2　超弹性铰链展开恢复曲线Fig.2 Deployment angle-time for double-layer tape-spring hinge

双层超弹性铰链由弯曲面相对的双层带簧叠加而成，一端固定，另一端固连长度为l1的刚性杆构成折展机构，如图3所示，按照图示方向折叠时内侧、外侧两层带簧将分别发生背向、对向弯曲，展开时内侧、外侧两层带簧分别发生对向、背向弯曲。双层超弹性铰链折叠时带簧弯曲变形存储弹性势能，展开时弹性势能转换为刚性杆和铰链的动能，在展开接近直线位置时若动能大于外侧带簧产生突然翻转所需要的能量，则外侧带簧将会发生背向弯曲。若能量不变，则带簧变形量随厚度增加而降低。图3中内侧两层带簧厚度均为w0，外侧两层带簧厚度分别为w1和w2。

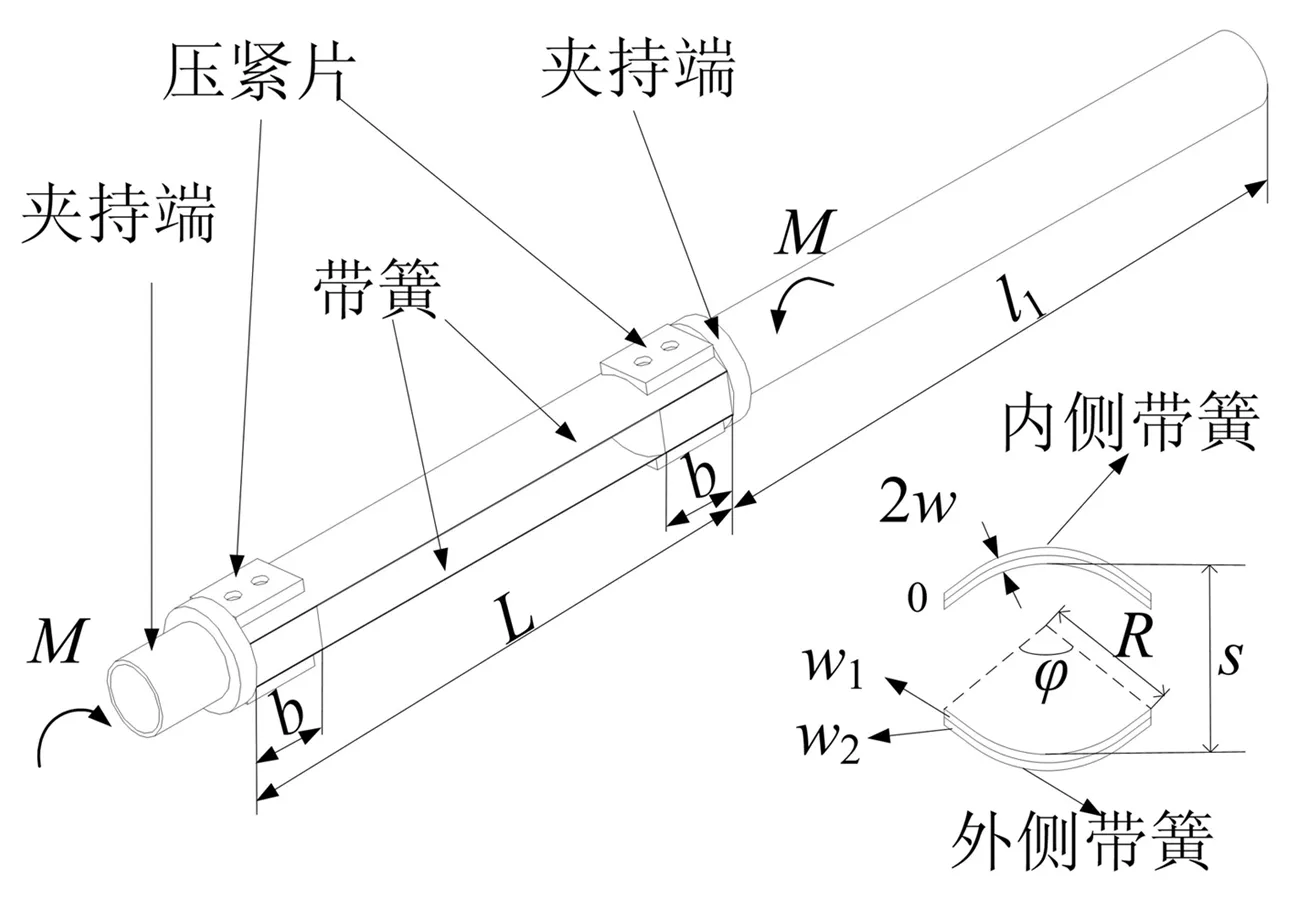
图3　含超弹性铰链的刚性杆几何示意图Fig.3 Geometry for the double-layer tape-spring hinge

在之前的文献[8-9]已经对影响冲击性能的其它因素进行了优化，如带簧横截面半径、中心角、分离距离等因素。根据Seffen对超弹性铰链折展时能量的分析，并考虑材料阻尼对能量耗散和固连刚性杆惯性力影响，通过改变外侧带簧厚度w1和w2研究双层超弹性铰链展开冲击特性。

2展开实验研究

图4为双层超弹性铰链展开实验装置示意图。测试的超弹性铰链横截面半径为17.8 mm，中心角为76°，横截面间距为16 mm，厚度均为0.12 mm。在精密光学平台上双层超弹性铰链一端固定，另一端连接着外径为22 mm和厚度为2.5 mm不锈钢刚性圆杆，在刚性圆杆中央连接一个球形滚轮，用于补偿重力对整个机构展开冲击的影响。

图4　展开实验装置示意图Fig.4 Dynamic deploying experimental setup

美国VRI公司生产的Phantom V12.1高速相机固定在双层超弹性铰链折叠区域正上方，用以记录展开过程中双层超弹性铰链变形位置和角度。双层超弹性铰链初始折叠角度为150°，高速相机采集速率设定为600 帧/秒。图5为双层超弹性铰链动力学展开过程中的位置图。

图5　双层超弹性铰链初始折叠150°时展开过程图Fig.5 Photos taken during deployment of double-layer tape-spring hinge folded 150 deg

3双层超弹性铰链动力学展开数值仿真

为了对超弹性铰链进行展开冲击分析，必须先把其折叠再进行展开动力学分析，而超弹性铰链折叠和展开过程是高度非线性的过程，分析耗时较长。为此，先采用仿真方法建立实验样本点，利用多项式响应面法建立双层超弹性铰链展开冲击特性的代理模型，再采用改进的非支配遗传算法进行多目标优化分析。

3.1双层超弹性铰链折展有限元模型

由于薄壁圆柱壳体类带簧结构大挠度弯曲是高度非线性过程，采用隐式求解器求解，将会遇到不收敛、数值稳定和奇异性等问题，而显示求解器可以避免这类问题的出现。所以，在ABAQUS中采用4节点缩减积分单元(S4R)建立有限元模型，如图 6所示，利用显示求解器(Explicit)进行求解。

图6　双层超弹性铰链有限元模型及边界条件Fig.6 Finte element model and boundaries for the DLTS hinge

为了简化模型，在双层超弹性铰链两端分别建立参考点，按照转动惯量相等的原则把夹持端质量等效到参考点上，通过施加运动耦合约束把参考点与周围区域连接，模拟夹持端进行加载。参考点2(RP-2)释放沿z轴移动的自由度和饶y轴旋转自由度，绕y轴旋转角度为166°。在超弹性铰链固定端通过shell to solid链接一个尺寸为30 mm×30 mm×12 mm固体，在靠近超弹性铰链通过网格划分出3层固体单元(C3D8)，在另一端布置一层无限单元(CIN3D8)，以此模拟实验中固定端中阻尼耗散对动力学展开能量的耗散作用。在分析中添加自接触(self-contact)以模拟折展过程中带簧之间的接触[10]，同时，为了提高计算效率，摩擦因数设置为零。

在ABAQUS中使用结构阻尼假设的动力学分析包括稳态响应分析和随机响应分析，瞬态动力学分析不能直接使用结构阻尼。而且，系统结构阻尼特性与结构内摩擦机理相关，在双层超弹性铰链有限元模型中带簧之间设置为无摩擦接触，整个模型中未考虑摩擦。铰链展开动力学冲击分析属于瞬态动力学分析，所以在冲击分析中与结构阻尼相关量均设为零，不会对结论产生影响。

3.2材料特性

双层超弹性铰链带簧材料为Ni36CrTiAl，是奥氏体高弹性合金，具有较高的强度和弹性模量、良好的耐腐蚀性。通过拉伸试验[8]测量出材料Ni36CrTiAl性能参数，见表1。

表1　超弹性铰链Ni36CrTiAl材料参数

3.3仿真模型验证

双层超弹性铰链准静态折展有限元模型在之前研究中已通过实验验证了准确性[8]。为了保证双层超弹性铰链展开时动能从零状态开始，在准静态折叠步之后增加能量耗散步，在展开步中的分析时间具有真实意义。仿真模型尺寸与实验测试件保持一致。图7为修正的有限元模型仿真值与实验值对比曲线。仿真与实验时超弹性铰链首次到达平衡位置的时间分别是0.275 s、0.278 s，过冲角度分别是82.21°、77.96°，完全锁定时间分别是0.752 s、 0.735 s，与实验值的相对误差分别为1.08%、-5.45%、-2.26%，表明修正后模型的准确性。

图7　仿真与实验恢复曲线对比Fig.7 Compared between simulation and experiment for rotation-time curves

4双层超弹性铰链展开冲击特性代理模型

响应面法(RSM)是统计方法和数学方法的结合，通过实验设计选取设计变量进行有限次试验得到样本点，然后对样本点进行数据拟合。通过响应面法建立代理模型，并对代理模型进行优化具有高效性，并且便于实现，在众多优化问题中得到应用[11-12]。

该研究中双层超弹性铰链展开冲击特性参数为最大应力Sf、冲击角θ和锁定时间t0，这些特性参数可以用如下的基函数表示：

(1)

(2)

式中,β0、βij、βiij、βiiij、βiijj分别为相应阶次基函数系数，i,j(j=1, 2, …,n)是第i,j个独立变量。

利用最小二乘法可以计算四次多项式函数的系数，

bf=(ΦTΦ)-1ΦTy

(3)

式中,bf是四次多项式函数的系数bf= (β1,β2, …,βN)，N是基函数φi序号。矩阵Φ由如下M个样本点构成，

(4)

式中,φN(x)M是第M个样本点的第N个基函数。

在以下分析中利用之前对双层超弹性铰链结构优化[8]的结果，双层超弹性铰链基本几何尺寸为：带簧横截面半径R=17.046 mm，横截面中心角φ=84.698 °，带簧分离距离s=19.844 mm，纵向长度L=126 mm，内侧两层带簧厚度固定为w0=0.12 mm。与双层超弹性铰链固连刚性杆的长度、外径和厚度分别为l1=165 mm、D=22 mm和t=2.5 mm，材料为铝合金，弹性模量E=70 GPa，泊松比σ=0.33，密度ρ=2.7×103kg/m3。

为了建立双层超弹性铰链展开冲击性能参数的代理模型，需要在设计空间中有足够的样本点。基于二因素五水平正交实验设计法对样本点进行设计，如表2所示。利用25组样本点将式(4)代入到式(3)可以计算出多项式函数系数，建立双层超弹性铰链展开冲击特性最大应力Sf、冲击角度θ和锁定时间t0关于外侧的内、外两层带簧厚度w1和w2的代理模型如下

(5)

表2　25组设计样本点的有限元结果

θ=-50 806.9+(1.46×106w2+

(6)

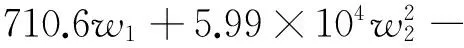
(7)

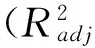
(8)

(9)

(10)

(11)

(12)

表3　设计样本点代理模型的精度评价

分析发现相关系数和复相关系数均大于0.98，相对误差不大于7.5%，表明代理模型具有足够的精度。

5超弹性铰链优化设计

双层超弹性铰链展开末端存在的冲击和锁定时间的长度会对其他结构产生影响，而折叠时应力集中现象会影响其使用性能和次数。超弹性铰链的带簧背向弯曲时折展过程力矩路径不同，与折展屈曲和突然翻转对应的弹性势能不同，带簧的厚度变化也改变屈曲和突然翻转的弹性势能。所以，选取双层超弹性铰链展开冲击角θ和锁定时间t0为目标函数，折叠最大应力Sf为约束变量，外层的内、外层带簧厚度w1、w2为自变量，建立如下优化模型：

(13)

目标函数fo，是各个目标分量fk及相应的权重因子wk与比例因子sk的和：

(14)

式中，k(k=1, 2, …,q)为目标函数序号，q(q=2)是目标函数分量的总数。如果对不同数量级的目标函数分量均选用相同的权重因子和比例因子，那么数量级较小对目标函数的影响会被削弱。所以，最大应力Sf、冲击角θ和锁定时间t0的比例因子分别选取为s1=0.5、s2=40.0、s3=0.25，权重因子分别为w1=w2=w3=1.0。在iSIGHT中采用改进的非支配遗传算法[13]对式(13)中模型进行多目标优化设计，设置种群代数为100，每代种群数120。图 8为双层超弹性铰链展开冲击优化的Pareto。

图8　Pareto最优解Fig.8 Pareto optimal results

由图8可知冲击角θ和锁定时间t0呈现负相关特性，冲击角θ增大时锁定时间t0变短。最优解为w1=0.138 mm、w2=0.129 mm，并计算该最优结构的有限元解与代理模型解、优化模型约束条件进行对比见表4。最优结构与代理模型的相对误差不大于5.008%，表明所选取的最优结构满足优化模型约束条件，且验证了该最优解的可用性和代理模型的准确性。

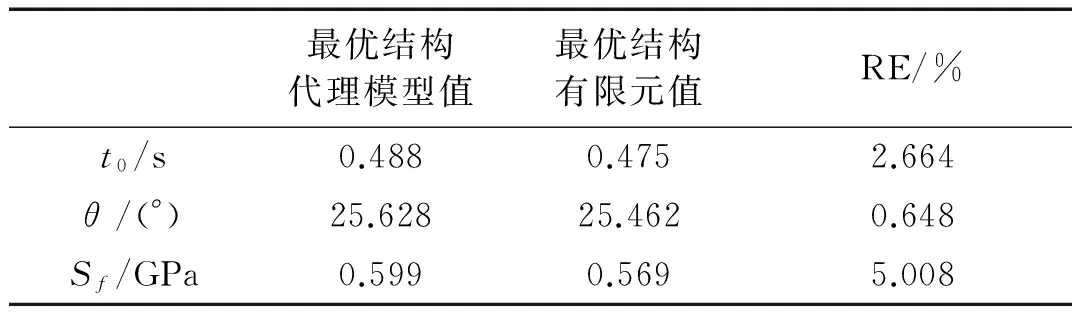
表4　最优解的代理模型和有限元模型结果对比

表4中列出最优解与等厚度双层超弹性铰链(表2中第13号样本点)有限元仿真得到的展开性能参数见表 5，等厚度结构和最优非等厚结构的展开角度-时间曲线进行对比如图9所示。

由表5和图9对比可知，最优非等厚结构使得双层超弹性铰链展开冲击角度降低52.154%，锁定时间缩短了29.104%，明显提高了双层超弹性铰链结构的展开性能。

表5　优化结构和初始等厚度结构展开性能参数对比

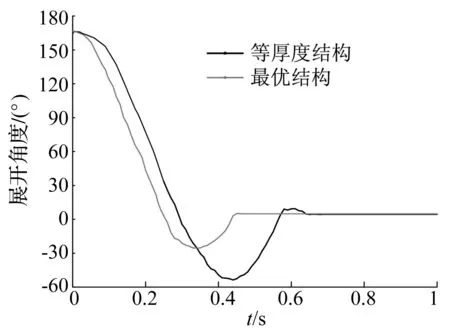
图9　优化结构和初始等厚度结构展开角度-时间对比Fig.9 Compared deployment angle-time curves between original and optimal configurations

6参数研究

根据表 2研究内层、外层带簧厚度w1、w2对双层超弹性铰链折叠最大应力Sf、展开冲击角θ和锁定时间t0的影响。进行参数研究的双层超弹性铰链基本几何尺寸为：带簧横截面半径R=17.046 mm，横截面中心角=84.698°，带簧分离距离s=19.844 mm，纵向长度L=126 mm，铰链折叠时发生背向弯曲的内侧带簧厚度均固定为w0=0.12 mm，刚性杆长度和外径分别为l1=165 mm和D=20 mm。超弹性铰链外侧两层带簧的厚度w1和w2变化范围均是从0.10 mm～0.14 mm。

图10和图 11分别为内层和外层带簧厚度w1、w2对超弹性铰链折叠最大应力Sf的影响曲线。可以看出，随着w1和w2的增加，Sf增加范围分别为6.333%～12.906%和12.044%～18.969%。

图10　外侧内层带簧厚度对最大应力的影响Fig.10 Effect of inner layer thickness on the maximum stress

图11　外侧外层带簧厚度对最大应力的影响Fig.11 Effect of outer layer thickness on the maximum stress

图12和图13分别为w1、w2对超弹性铰链展开冲击角θ的影响曲线。从图中可以看出，θ随着w1和w2的增加而降低的范围分别为47.211%～66.925%和50.154%～68.770=%。

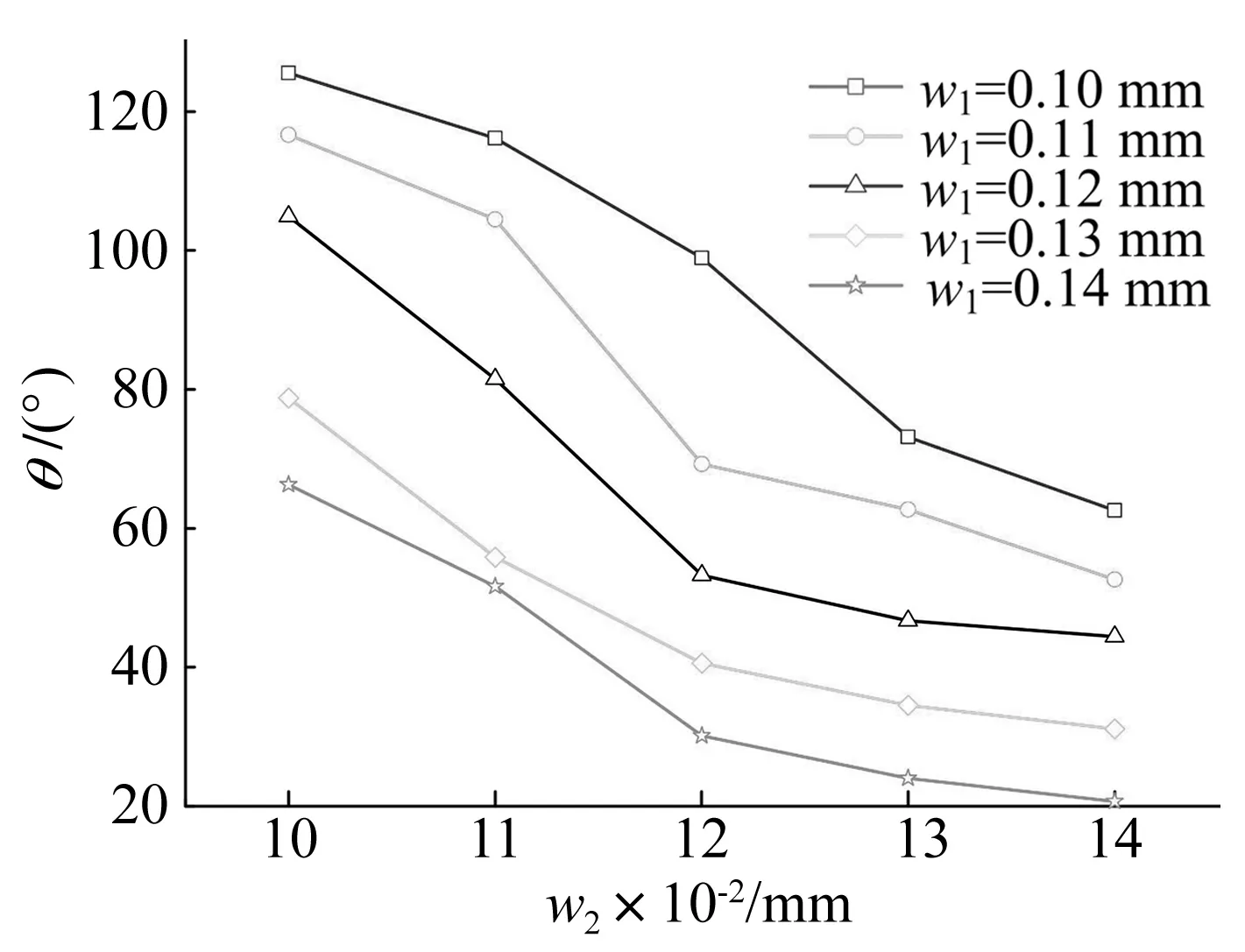
图12　外侧内层带簧厚度对冲击角度的影响Fig.12 Effect of inner layer thickness on the shock angle

图13　外侧外层带簧厚度对冲击角度的影响Fig.13 Effect of inner layer thickness on the shock angle

图14和图15分别为w1、w2对超弹性铰链展开锁定时间t0的影响曲线。从图中可以看出，t0随着w1的增加先降低后增加，t0先降低的范围为26.866%～35.484%，之后t0增加的范围为3.571%～7.843%；t0随着w2的增加先降低后增加，t0先降低的范围为17.460%～27.957%，t0后增加的范围为3.175%～5.769%。

图14　外层内层带簧厚度对锁定时间的影响Fig.14 Effect of outer layer thickness on the locked time

图15　外侧外层带簧厚度对锁定时间的影响Fig.15 Effect of outer layer thickness on the locked time

通过对双层超弹性铰链展开冲击特性进行参数研究发现，外侧两层带簧片厚度w1、w2对其折叠最大应力Sf、展开冲击角θ和锁定时间t0的影响都很显著：随着厚度w1、w2增加，Sf增大，θ降低，而t0则是先降低后增大。主要是由于折叠时内侧产生背向弯曲的带簧厚度不变，相当于折叠存贮的弹性势能不变，而外侧带簧厚度越大在展开发生突然翻转时产生相同变形需要的能量越大，所以冲击角度随着外侧带簧厚度增大而降低。但是外侧带簧厚度过大时产生突然翻转产生相同变形量存储过多的弹性势能，会导致双层超弹性铰链二次冲击角度增大，进而使其锁定时间增加。

7结论

基于ABAQUS/Explicit有限元软件，以降低双层超弹性铰链展开冲击角度和缩短锁定时间为目标，以外侧两层带簧厚度为设计变量进行优化设计，并对展开冲击性能进行参数研究，得到如下结论：

(1) 搭建实验平台对双层超弹性铰链进行动力学展开性能测试，基于实验结果对有限元模型进行了修正，保证了仿真分析的准确性。

(2) 基于有限元仿真结果，利用四次多项式响应面法建立双层超弹性铰链展开冲击性能代理模型，误差不大于7.543%，表明代理模型能够精确表征双层超弹性铰链外侧带簧厚度和展开冲击性能之间的关系。

(3) 以双层超弹性铰链展开冲击角度最小和锁定时间最短为目标函数，以外侧两层带簧厚度为设计变量进行展开冲击性能优化，得到了最优非等厚双层超弹性铰链结构参数，与等厚度双层超弹性铰链相比最优结构展开冲击角度减小了52.154%、锁定时间缩短了29.104%。

(4) 基于正交试验设计对双层超弹性铰链展开冲击特性进行参数研究，发现外侧两层带簧片厚度增加时，最大应力增大、展开冲击角θ降低，而锁定时间t0则是先降低后增大。

参 考 文 献

[1] Lane S A,Murphey T W,Zatman M. Overview of the innovative space-based radar antenna technology program[J]. Journal of Spacecraft and Rockets,2011,48(1):135-145.

[2] Anon. Hughes graphite antennas installed on Mast-2 craft[N]. Space News,Nov. 1994.

[3] Adams D S,Mobrem M. Lenticular jointed antenna deployment anomaly and resolution onboard the Mars Express Spacecraft[J]. Journal of Spacecraft and Rockets,2009,46(2):403-410.

[4] Seffen K A,Pellegrino S. Deployment dynamics of tape springs[J]. Proceedings of the Royal Society of London,Series A:Mathematical and Physical Sciences,1999,455(1983):1003-1048.

[5] Soykasap O. Deployment analysis of a self-deployable composite boom[J]. Composite Structures,2009,89:374-381.

[6] Yao X F,Ma Y J,Yin Y J,et al. Design theory and dynaimic mechanical characterization of the deployable composite tube hinge[J]. Science China:Physics,Mechanics and Astronomy,2011,54(4):633-639.

[7] Mallikarachchi H M Y C,Pellegrino S. Deployment dynamics of ultrathin composite booms with tape-spring hinges[J]. Journal of Spacecraft and Rockets,2014,51(2):604-613.

[8] Yang H,Liu R Q,Wang Y,et al. Experiment and multiobjective optimization design of tape-spring hinges[J]. Structural and Multidisciplinary Optimization,2015,51(6):1373-1384.

[9] Yang H,Deng Z Q,Liu R Q,et al. Optimizing the quasi-static folding and deploying of thin-walled tube flexure hinges with double slots[J]. Chinese Journal of Mechanical Engineering,2014,27(2):279-286.

[10] Mallikarachchi H M Y C,Pellegrino S. Quasi-static folding and deployment of ultrathin composite tape-spring hinges[J]. Journal of Spacecraft and Rockets,2011,48(1):187-198.

[11] Hou S J,Liu T Y,Dong D,et al. Factor screening and multivariable crashworthiness optimization for vehicle side impact by factorial design[J]. Structural and Multidisciplinary Optimization,2014,49:147-167.

[12] Li M,Deng Z Q,Guo H W,et al. Crashworthiness analysis on alternative square honeycomb structure under axial loading[J]. Chinese Journal of Mechanical Engineering,2013,26(4):784-792.

[13] Deb K,Pratap A,Agarwal S,et al. A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.

Dynamic analysis and optimization for double-layer tape-spring hinges unfolding

YANG Hui, GUO Hong-wei, WANG Yan, LIU Rong-qiang, TAO Jian-guo

(State Key Laboratory of Robotics and System, School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150080, China)

Abstract:Flexible tape-spring hinges can be folded elastically and can self-unfold by releasing stored strain energy with fewer component parts and slight weights. The unfolding dynamic behaviors of double-layer tape-spring (DLTS) hinges were studied and optimized to reduce unfolding shock. A platform for unfolding test of DLTS hinges was built and tests were performed to verify the correctness of the FE numerical model for double-layer tape-spring hinges. The unfolding shock angle and the locked time were taken as objectives, the thicknesses of outer layer tape-spring and inner layer one in outer bending direction of a DLTS hinge were taken as design variables. The modified non-dominated sorting genetic algorithm was employed to conduct the optimal design of DLTS hinges. The finite element models for the non-equal thickness optimal design based on numerical methods were established and validated. The optimization results had relative errors no more than 5.008%. Comparing unfolding behaviors of the non-equal thickness optimal design and those of the equal thickness one for DLTS hinges, it was shown that the unfolding shock angle and locked time for the former reduce 52.154% and 29.104%, respectively; after optimization, the shock of the structure is reduced obviously. The parameter study showed that the unfolding shock angle is more sensitive to the outer layer thickness of tape-spring, and the locked time decreases firstly and then increases with increase in the thickness of tape-spring.

Key words:unfolding shock; double-layer tape-spring hinge; dynamic analysis; optimization; spaceborne antenna

基金项目：国家高校111计划(B07018)；机器人技术与系统国家实验室自主课题(SKLRS201401A02)；中央高校基础研究基金(HIT.NSRIF. 2015050)

收稿日期：2015-01-27修改稿收到日期：2015-05-22

通信作者刘荣强 男，博士，教授，1965年生

中图分类号:V214.3+6

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.09.004

第一作者 杨慧 女，博士生，1986年6月生