物理系统中随机效应:混沌和随机共振
颜士敏+曹振兴

【摘 要】针对现代统计物理中两种非线性动力学行为,即混沌和随机共振,本文利用数值解法进行了模拟和解释。混沌是确定性系统中内禀随机性的一种体现,深化了人们对必然和偶然的认识,而随机共振是随机系统的内在有序性体现,改变了人们对于噪声的观念,证实了噪声对于系统序的建立具有建设性作用。这些结果对于学生通过物理计算更好地理解物理系统特性具有参考意义。
【关键词】混沌;随机共振;确定性系统;随机系统
【Abstract】Aiming to comprehend the nonlinear behaviors in modern physics, this paper utilizes the numerical method to illustrate the chaos effect and the stochastic resonance phenomenon. Chaos demonstrates the internal randomness of deterministic systems, which develops our view on occasionality and inevitability. While, stochastic resonance is the cooperative effect in the random systems, and the benefits of noise in certain nonlinear systems are adequately appreciated. These results are interesting for students to understand certain physical systems clearly via the physical calculations.
【Key words】Chaos; Stochastic resonance; Deterministic system; Random system
在混沌动力系统学建立之前,物理学家认为微分方程的确定性解可以描述自然现象,只要收集到初始数据,那么系统未来状态是完全可以预测的[1-2]。基于统计原理的量子力学首先打破了上述确定论观念,而混沌概念和涨落唯象理论的提出,使得人们意识到确定性系统也可以出现随机性结果[1-3]。经过近50年的发展,物理系统中内禀随机性和非平衡态随机效应已经成为现代统计物理理论的前沿研究问题[1-3]。 本文利用计算机模拟物理系统中混沌和随机共振两类随机效应,前者是物理系统内禀随机性引起的,其本质是物理系统对于初始条件的敏感性,而后者是微观涨落运动对于物理系统宏观变量演化的一种作用机制。我们通过微分方程的数值解法形象地解释了上述两种随机效应,达到学生通过物理计算更好地理解物理系统动力学性质的目的。
1 物理系统内禀随机性:混沌
20世纪50年代,美国麻省理工大学气象学家洛伦兹研究大气流体流动模型,从而解释物理参数变化对天气预报结果的影响。由于时代的限制,当时的单行打印机打印速度非常慢,每10秒钟才能打印一行。为了加快计算,洛伦兹只打印了部分数据,虽然计算机计算到小数点后六位,而洛伦兹打印结果只精确到三位数,他认为舍去的数字并不会影响系统解的精度,将经过舍位之后的计算机计算结果作为初始值中途输入计算机继续计算。按照确定论观点,这样得到的计算结果应该和计算机原来运行结果应该是一致的。然而,洛伦兹发现新一轮的计算机计算结果很快从初始值处发生扩散。经过深入研究,洛伦兹认为问题的根源在于系统对于初始条件的敏感依赖性,即使初始值的微小变化,经过系统之后,系统解轨迹出现巨大差别,这一现象非常好地解释了天气预报的复杂性[1-3]:初始条件的任何误差被系统迅速放大,以至于具有实际价值的可预测性大大降低。这类系统的内禀随机性被称为混沌现象[1-3],它比纯粹的可预测性更加符合我们的日常经验,比如中长期的天气预报准确率是非常低的,因为天气初始条件微小变化使得几周之后天气情况在本质上是无法预测的[1-3]。
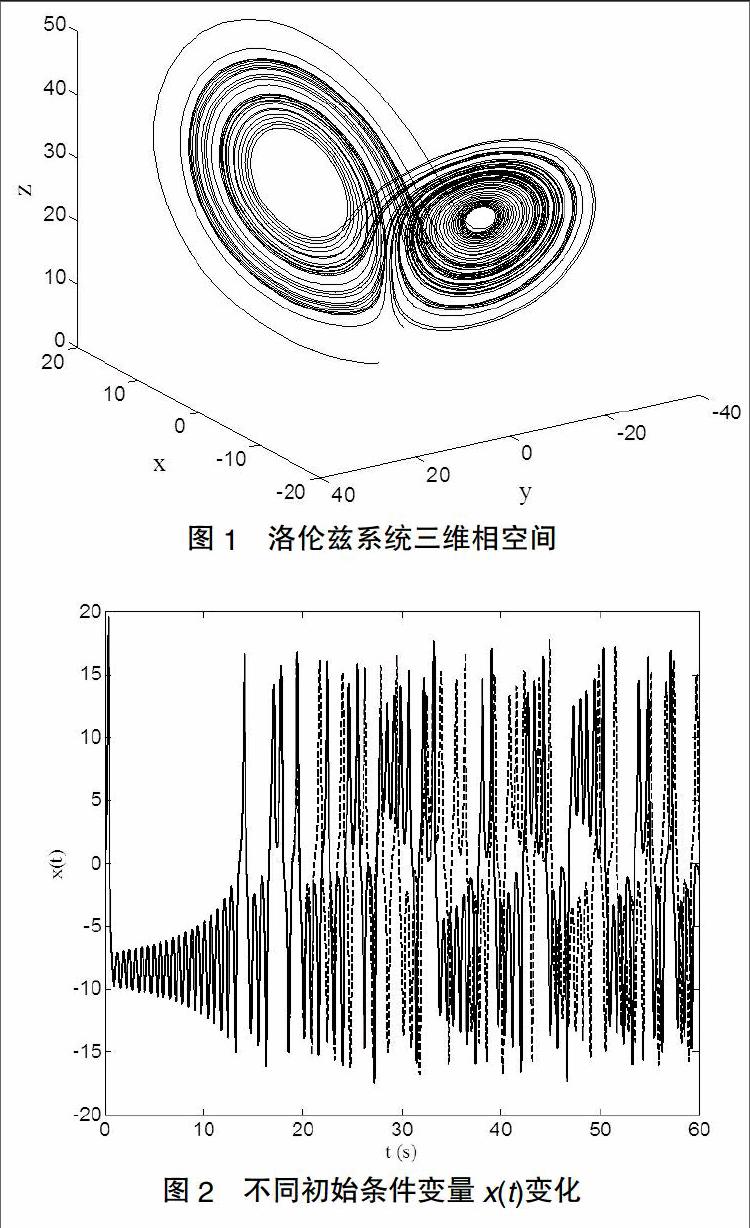
变量x(t)和y(t)与大气温度的竖直和水平变化相关,而变量z(t)与大气对流有关,σ是普兰特数,γ是规范化瑞利数,而常数b和研究区域的几何形状相关[1-3]。该确定性系统只有线性项和二次项,没有外部随机性输入,然而此系统有着复杂的类随机动力学行为。比如取参数σ=10,γ=28,b=8/3,其轨迹完全由上述参数和初始条件(x0,y0,z0)确定,但是其特性很难预测。方程(1)的数值解法采用4阶龙格-库塔法,如图1所示,初始条件为(1.01,1.0,1.0),洛伦兹系统三维相图表明其轨迹在三维相空间中是有界的,但是无周期性且不相交,混乱地来往于两个吸引子之间。这是因为整体上系统能量是耗散的,其轨迹趋向一个零体积集合,而两个吸引子是不稳定的,导致其轨迹的不断褶叠、翻转和延伸,因此出现了总体的混沌现象。这类系统的内禀随机性表现在初始值的敏感性:即使初始值的微小变化经过系统放大之后,随着时间的变化二者的轨迹出现完全不相干的性质。比如将初始条件(1.01,1.0,1.0)改为(1.011,1.0,1.0),如图2所示,在两种初始条件下变量x(t)随时间演化,尽管其误差仅有1‰,但是二者轨迹在21秒处发生改变,实线和虚线分别代表上述两类不同初始条件下的状态变量演化,随着时间继续增加,x(t)状态发生很大改变且没有相关性,其他变量y(t)与z(t)也类似,这也是混沌系统长时间行为不可预测的本质。
2 随机系统的内在有序性:随机共振
随机共振概念最早是由邦济[4-5]在研究太阳对于地球的随机作用力是如何引起冰川期和暖期的周期性变化时提出的。地球的冰川期大约105年,这个周期和地球由于星系间的引力引起的轨道偏心率一致,但是偏心率不足以使得地球气候发生如此大的变化。邦济发现由于地球每年气候涨落(如太阳的辐射)而引起的气候变化和偏心率能够达到了一种“共振”,从而使得地球的冰川期和暖期发生周期性变化,此现象称为随机共振现象。随机共振现象第一次证实了随机涨落对于宏观变量(如地球气候)影响能够起到决定性作用[4-5]。
经典随机共振模型为质量是m粒子在双稳态势阱内运动过程,其随机微分动力学方程满足[4-5]:
当阻尼系数λ>>m,称为过阻尼系统,不失一般性地设λ=1,式(2)可简化为一阶随机微分方程:
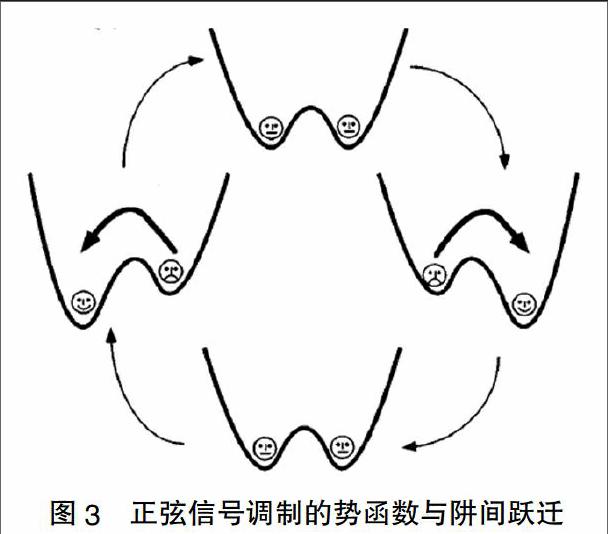
这里信号为s(t),白噪声ξ(t)的强度为D,数值解法采用Euler-Maruyama随机微分解法[4-5]。双稳态对称势函数V(x)=-x2/2+x4/4,具有两个稳态xm=±1和能量势垒ΔV=1/4,当信号s(t)存在时,此势函数成为被s(t)调制为V(x,t)=-x2/2+x4/4-s(t)x。设弱信号s(t)=Acos(Ωt)的幅值A<和频率Ω<<1,势函数V(x,t)的变化如图3所示,对应幅值从零变化为+A,然后又从零变化为-A的过程。在没有噪声的帮助下,此信号不能够使得粒子越过势垒达到另外一个稳态,也就是说粒子是不能进行阱间跃迁的。然而,随着噪声ξ(t)的加入,粒子能够从相对浅的势阱进入相对深的势阱里去,当噪声强度达到一个最优值时(如图4中噪声强度为D=0.09),此时系统响应如信噪比、响应幅值等达到最大值,我们可以看出此时系统输出x(t)能够从统计意义上反映了信号幅值正负的周期变化。故借鉴力学中“共振”一词,称这种现象为随机共振。随机共振现象表明,在非线性系统中,外部噪声环境有时不是系统性能的阻碍,反而是一种积极的促进,能够使得系统特性和输入微弱信号达到协同,成为建设系统序的重要因素,这也是非线性系统内在随机性向有序性转化的有力例证。
3 总结
上述两种随机效应给现代物理带来了巨大冲击:一是,混沌打破了物理学以往可预言的确定论观点,它让人们理解了某些物理系统长时间预测是无意义的,系统内部的随机性深化了人们对必然和偶然的认识,更全面地理解自然界的统一性;二是,随机共振打破了噪声是有害的观念,在某些非线性系统中噪声能出人意料地产生积极影响,对于系统的演化反而起到决定性作用,对于系统序的建立是有益的,使得人们更加重视微观尺度的运动对于宏观量演化的影响,而不能简单地依据尺度和强度大小而忽略它。简言之,混沌表现了确定性系统的内禀随机性,而随机共振表现了随机系统的内在有序性,本文通过这两类物理现象计算,使得我们能够达到更好地理解物理系统的两类随机效应。
【参考文献】
[1]R.C. Robinson. An Introduction to Dynamical Systems[M]. New Jersey: Pearson Education, Inc, 2004:207-244.
[2]胡岗.随机力与非线性系统[M].上海:上海科技教育出版社,1994:219-254.
[3]刘式达,梁福明,刘式适,辛国君.自然科学中的混沌和分形[M].北京:北京大学出版社,2003:1-70.
[4]R. Benzi, A. Sutera, and A. Vulpiani. The mechanism of stochastic resonance[J]. Journal of Physics A: Mathematical and General, 1981: L453-L457(14).
[5]L. Gammaitoni, P. Hanggi, P. Jung, F. Marchesoni. Stochastic resonance[J]. Reviews of Modern Physics, 1998:233-287(70).
[责任编辑:汤静]

