深刻体验 深入思考 深化认知——“圆的认识”教学思考与实践

◇李培芳

深刻体验 深入思考 深化认知
——“圆的认识”教学思考与实践

◇李培芳

课前思考

“圆的认识”是北师大版教材六年级上册的内容。圆对小学生来说是认识图形的一次飞跃，看似简单，其实并不容易。人类对圆的认识也经历了漫长的历程：约在六千年前，美索不达米亚人做出了世界上第一个轮子——圆形的木盘。在四千多年前，人们将圆形的木盘固定在木架下，这就成了最初的车子。会做圆，但不一定就懂得圆的特征。一直到两千多年前我国的墨子 （约公元前468—公元前376年）才给圆下了一个定义：圆，一中同长也。这个定义比希腊数学家欧几里得（约公元前330—公元前275年）给圆下的定义要早一百多年。

探寻圆的特征为什么会这么难？难在哪？

在很多课堂里，教师组织学生通过折一折、量一量、画一画等活动探索圆的特征，学生一般不费吹灰之力就能概括出圆的特征，非但不难，从学生的学习状态中甚至可以看出他们并不认同这是一个有挑战性的问题。我曾找来几个二年级的孩子，让他们观察折后的圆，他们也能发现折痕（半径或直径）都相等。

其实，难的不是发现半径都相等，而是从一个什么标记也没有的圆上发现半径、圆心的存在！

能不能让学生也经历这个认知过程？即便想不出来，经历也是有意义的，一旦学生从探而不明、思而不得的强烈体验中找到圆的本质特征，或许会更折服于数学家独特的数学思考。这种经历会让学生对圆的特征的认识更深刻，并从学习中感受到一种可贵的思维方式。

所谓可贵的思维方式，指的是人类对圆的特征的概括的思维方式。圆的特征的概括与直线图形特征的概括完全不同。直线图形的特征大都从图形的各组成要素（如正方形的边、角）去概括。圆的特征显然无法从其组成要素（即一条封闭曲线）去概括，这就需要另辟蹊径。圆的特征概括的是圆上的点的共同属性，这就需要人们的认识在以下两个方面实现超越：一是对线的认识的超越，要将线看成是点的集合；二是图形特征认识的超越，将对图形特征观察的视角锁定在组成图形的点的共同属性上。

这些认识对学生来说或许超出其认知的可能，然而，即使探索不出，经历这样的思考过程仍然是有意义的。探而不明而后欣赏前人的探索成果对学生来说也是很好的学习方式。伴随着这样的学习过程还可能激发学生“见贤思齐”的心向。

此外，圆的特征有很多，诸如 “圆有无数条半径、直径，半径、直径都相等”“直径是半径的2倍”“圆有无数条对称轴，直径所在的直线是圆的对称轴”“圆心确定圆的位置，半径决定圆的大小”等。这些特征大都是并列出现，然而对于六年级的学生，能否将圆的特征“结构化”，如将“一中同长”作为核心特征，其他特征作为核心特征的推论，运用推理（且尽可能运用演绎推理）思考圆的其他特征，这有点公理化思想的意味。这样“递进式”认识圆的特征的学习对学生更有挑战性，也是更富有意义的。

对于“同圆”与“等圆”，笔者十分赞同华应龙老师的处理，华老师以在表达“人的两只脚是一样长的”时无需说明是“同一个人”予以类比更是妙不可言！不同的圆其半径一定相等吗？这对于六年级的学生是无需思考的问题。

还有，对于画圆的教学，不要以为这是学生完全可以自己通过练习形成的技能，在课上不必要花费太多时间。在课后设计诸如 “用圆设计一幅美丽的图案”就可以让学生在快乐的创造中形成画圆的技能。实践证明，大部分学生在买到圆规后就已经“急不可耐”地“画圆”了！

课堂实践

一、经验唤醒，外化认知

师：同学们，今天我们要认识圆，想一想，大概在什么时候你就认识圆这个图形了？

生：一年级。

生：幼儿园。

师：是啊，大家很早就认识圆了，请看老师手中的这个图形（出示椭圆），这是一个圆吗？

生：不是，这是椭圆。

（大家都点头赞同）

师：再看这个图形（如图1），是圆吗？

图1

生：（齐）是。

师：同学们，你们被骗了，这不是圆！（学生一脸惊讶）老师这里有一把尺子，谁能用数据说明“这不是圆”？

（一位同学上台分别量出上图的长轴与短轴，并分别报出数据是22cm与23cm）

师：有什么想说的吗？

生：看上去像圆的图形未必是圆。

生：要测量才能判断。

师：是啊，学数学不能只凭观察就作判断。

教学意图：“熟悉未必熟知”（罗杰斯），对于圆，学生更多的是感性的认识，本课的目的恰恰在于引导他们从感性走向理性，从量的角度思考与刻画圆，这个“似圆非圆”的陷阱，有张力更有冲击力，学生的学习一瞬间“从眼睛走向大脑”，从观察走向思考。

二、比较想象，重建认知

师：（课件出示图2）现在，我将一个特别标准的圆放在一堆图形里，你能将这个圆找出来吗？

图2

生：第一个图形是圆。

师：圆与其他图形最大的不同是什么？

生：圆是弯的。

生：圆没有角。

生：圆有无数条对称轴。

师：刚才有的同学说“圆是弯的”，没错，圆是曲线图形！不过，当圆对着其他图形说“我是弯的”，你想，谁该有意见了？（生：椭圆）椭圆会怎么说？

生：我也是弯的啊！

生：当圆说“我没有角”，椭圆会说“我也没有角”。

师：我们貌似找出了圆的特征，不过，分析、比较后发现，这些并不是圆最大的特征。再想想！

（沉默！长时间的沉默……）

师：同学们，这个问题想不出来是不奇怪的。人们早在四千多年前就能做出圆形的轮子，但是会做圆，不一定就懂得圆的特征。一直到两千多年前我国古代的思想家墨子才说出了圆的特征，这中间经历了两千多年啊！所以，同学们继续想，老师愿意等。

（沉默！长时间的沉默……）

生：（小声地）是不是圆边上到圆中心的距离是一样的？

师：请你再大声地说一遍！

生：圆边上到圆中心的距离是一样的。

师：这句话来自两千多年前啊！你愿意上讲台来边比边说吗？

（学生上台比画，课件同步动态出示图3）

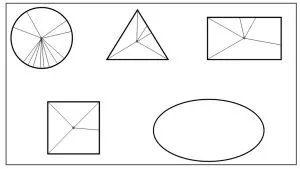
图3

师：墨子概括了圆的这个特征：“圆，一中同长也！”谁来说说对这句话的理解？

生：就是说圆有一个中心，从圆上的点到中心点的线段都一样长。

师：是啊！这是圆最独特的特点，人们还将圆的这个中心点称为“圆心”，用字母O表示，这条相同长度的线段称为“半径”，用字母r表示。接下来，请大家在老师给你们准备的圆上，画出一些半径来，量一量，看这些半径是不是都相等。

（学生活动后，讨论得出：圆有无数条半径，所有的半径都相等）

教学意图：选择如此“纠结与困难”的教学是基于后测，笔者在六年级的两个班（已学过圆的周长与面积的计算）做了后测，100人参加，在回答“圆最大的特征是什么”时，只有3人回答“所有的半径都相等”，大部分学生的回答是“圆是曲线图形”“圆没有角”等。可见，学生在学习“圆的认识”时，对圆的特征没有深刻的数学体验。之所以没有深刻的体验，一方面是圆的特征被割裂开来认识了，先是认识圆的各部分名称，再分别探索半径与直径的特征，很多学生认为“所有的半径都相等”是半径的特征；另一方面是学生对圆的特征的认识太“流畅”了，没有困难，没有疑惑，太“流畅”的学习往往是无痕的。

三、尝试推理，丰富认识

师：圆内还有一条很重要的线段，叫作直径。（认识“直径”略）从“圆有无数条半径，所有的半径都相等”出发，可以推导出什么结论？

生：圆有无数条直径，所有的直径都相等。

师：（出示图4）这几条线段，你认为哪一条最长？

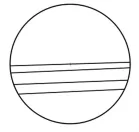
图4

生：最上面的线段最长。

生：直径最长。

师：为什么？

生：因为直径在最中间，所以直径最长。

师：为什么在最中间的就是最长的。

生：因为往下就越来越短了。

师：凭什么确定往下就越来越短了？

（生沉默）

师：哈哈，是不是要说用眼睛看出来的啊？一上课我们就上眼睛的当了。其实重要的东西往往是眼睛看不到的，要用脑子想！请看屏幕，有没有什么启发？（出示图5）

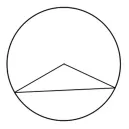
图5

生：我知道了，三角形两边之和大于第三边。（讨论略）

师：真好！继续观察！（出示图6）

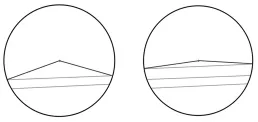
图6

生：这些线段的两端与圆心相连就组成一个三角形，三角形两边之和大于第三边，它们的长度就比两条半径相加的和要短，而直径的长度相当于两条半径，所以直径最长。

师：这样，我们又得出一条重要的结论——“圆内最长的线段是直径”。

教学意图：小学数学“图形的认识”因受限于学生逻辑思维能力发展水平，大多停留在观察与操作层面，缺乏深入的数学思考。笔者认为，到了六年级，学生尝试通过演绎推理深入探索图形的特征不仅是有可能的，而且是有价值的。

四、运用知识，内化认知

师：（出示图7）海平面下有一处暗礁要实施爆破，你能画出危险的区域吗？请大家拿出学习单，画出危险的区域。

图7

（学生操作，教师巡视）

师：说说你们是怎么画的。

生：危险的区域是一个圆，圆心在点B，半径是3cm。

师：如果你画得准确的话，你的圆一定会刚好经过点 A，因为线段 AB的长度刚好是3cm。检查一下自己画得对不对。

师：这里的两条信息，哪一条最重要？

生：两条信息都重要，如果没有“信息1”就不知道这个圆要画多大；如果没有“信息2”就不知道这个圆的圆心在哪里，也就没法画了。

师：看来，要确定一个圆，我们既要知道它的——圆心（生答），还要知道它的——半径（生答）。圆心确定了圆的位置，半径确定圆的——大小（生答）。

（出示第二个问题：一艘船离点A6.5km，这艘船处在危险区域内吗？大部分学生说“不在危险区域内”，小部分学生在思考）

师：这艘船到底在哪里能确定吗？（生：不能确定）同桌合作，把这艘船可能处的位置都画出来，这样就能确定它是不是处在危险区域了。

生：不可能都画出来的。船可能在上面，也可能在下面、左面、右面，没办法都画出来。

师：试试吧，不要直接就放弃啊！

（学生操作，一会儿部分学生大喊：是一个更大的圆。大部分学生完成后交流发现，船可能处的位置是在一个以点A为圆心，6.5cm为半径的圆上，不处在危险区域内。如图8。过程略）

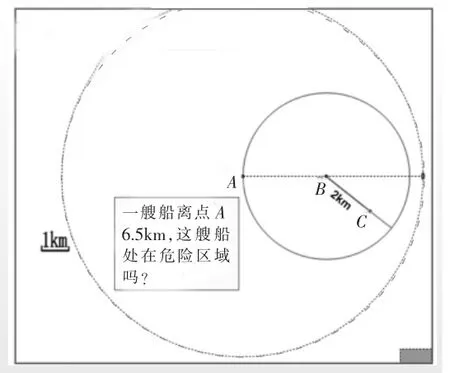
图8

教学意图：高水平的认知表现为学习者可以随时提取相应的知识解决问题。本环节通过富有挑战性的问题，促使学生提取出对圆的相关认知解决问题，这其中包括“圆的特征”“半径与直径的关系”“画圆”“圆内最长的线段是直径”等。不难看出经由这样的学习，学生对圆的认识是丰富且深刻的。同时也促进了学生对圆的认识更加融会贯通，走向融合化与结构化，从而进一步促进认知的深化。

（作者单位：福建厦门市华昌小学）