让“算理”和“算法”无缝对接——“两位数减两位数（退位）”案例与评析

◇执教/王闽 评析/南欲晓

让“算理”和“算法”无缝对接
——“两位数减两位数（退位）”案例与评析

◇执教/王闽 评析/南欲晓

一、课前思考

（一）教材解读。

两位数减两位数的退位减法是人教版教材二年级上册第19页例2、例3的内容。教材编排中提出两个问题。问题1：个位不够减，如何退位？教材意图是让学生通过操作来理解算理，掌握算法。但是两位数减两位数的笔算作为一种模型，如何引领学生经历模型的产生、形成、应用和发展的过程呢？如何恰当地处理好“学具操作—几何直观”和“算理直观—算法抽象”之间的关系？问题2：从十位减起方便吗？教材设置了这个问题，但没有对应的环节和素材来帮助教师实施教学，达成目标。因此教学时更多的教师把从个位减起作为一种规定让学生记住，很难也很少去探究形成的原因。

（二）学生调研。

我们对一所农村学校二年级的38个学生进行了学前调查和访谈。调查内容是：“计算65-37=□，并回答：当个位不够减时怎么办？”调查结果如表1所示。

表1

从计算的结果来看，34.2%的学生的计算结果是正确的。近84.2%的学生已经有退位的意识,知道“请十位帮忙”。从数据看，学生有退位的“意识”。由对个别学生的访谈可发现：学生能用小棒操作表示退位的过程，但无法用竖式表达退位的过程。看来在学生原有的知识经验中，退位减法的算理和算法似乎处于“平行线状态”，动手操作和运算是互相分离的，并不能自主地在算理和算法之间自然地建立起一一对应的联系。对于运算顺序，学生并没有觉得“从个位算起比较方便”，他们认为这只是一种人为的规定，学生给出的回答是:“老师，前面教加法竖式的时候就跟我说了计算时要从个位算起。”

二、教学过程

（一）创设情境，引出问题。

1.11月份最受欢迎的三部儿童电影，你更喜欢哪一部？（课件出示图1）

图1

2.获取信息，提出问题，列出算式。

3.根据学生的回答，教师板书算式：38-34，56-34，56-38。

（二）复习旧知，做好铺垫。

1.口算38-34，并说说口算过程。

2.笔算56-34。

（1）学生独立列竖式计算，说计算过程。

（2）小结：不管怎么算，都要做到数位对齐了再相减。

【评析】用学生喜欢的情境引入新课，回忆不退位减法的核心是相同数位上的数直接相减，这是减法的基本算理。

（三）动手操作，感悟算理。

1.过渡：谁会算56－38呢？

2.尝试计算，了解学生。

学生独立计算后，教师请三个学生上台板演。学生可能出现的结果如图2所示。

图2

3.操作感知，动作表征。

（1）操作任务：同样是56－38，怎么会出现3种不同的结果呢？我们请小棒来帮忙找出正确的答案。（出示小棒图和操作要求）

①静静地想想，该怎么从这里拿走38根小棒呢？

②同桌合作边摆边说，并与同桌商量好怎么说给全班同学听。

（2）操作反馈：请两个学生上台演示摆的过程，其他同学仔细观察，看看他们摆的过程有什么相同和不同的地方（两种不同的摆法：先拿掉3捆，再拿8根；先拿掉8根，再拿3捆）。

4.课件演示，语言表征。

（出示课件）分步演示学生的两种不同摆法（如图3），分别对每一步进行语言表征并归纳总结。

图3

（1）6－8不够减，怎么办？

学生想到“退”：当发现个位6减8不够减，也就是在拿8根小棒的时候，这儿只有6根，不够拿，所以去拿了1捆，也就是从十位上退了“1”。

（2）从十位上退1后，怎么变可以拿走8根？

生：把1捆拆开以后变成10根，再与原来的6根合在一起变成了16根，捆数从原来的5捆变成了4捆。也就是个位变成16个“一”,十位变成4个“十”。

（3）个位上现在是多少根，够减吗？

生：从16根里拿走8根，从4捆里拿走3捆，也就是个位上16个“一”减去8个“一”，十位上4个“十”减去3个“十”，这样够减了。

（4）分步演示第一种摆法，即先拿掉3捆，再拿8根。拿8根的过程同上。

（5）引导学生发现两种拿法都很棒，再比较在拿的过程中有什么相同的地方与不同的地方。

反馈：相同点是，拿8根小棒的时候都用了“退”和“变”的方法；不同点是，拿的顺序不一样（先拿“捆”与先拿“根”）。

【评析】退位减法思维过程的第一步是将“退位减法”转化成不退位减法，这是学习新知的要点。借助小棒操作，让学生的思维过程尽可能实现“可视化”，并在教师的引导下，体会转化的步骤可以分解成“发现不够—去拿1捆—拆成10根—跟原来的根数合并”这样的四步，完成了从“不够减”到“够减”的转化，也就是让新知变成了旧知。因此，实现转化是算法的立足点，更是实现退位减法的核心。

（四）对比发现，形成算法。

1.形成竖式，抽象算法。

师：你能结合两种不同拿法的过程，用竖式计算的方式表示出来吗？

（课件演示操作过程，教师辅助形成两种不同的竖式计算，如图4所示）

图4

小结：两种不同的拿法变成了两个不同的竖式计算，它们最大的不同是什么？你更喜欢哪一种？为什么？以后遇到这样的题目，你会从哪一位算起？

【评析】从操作层面看，用“摆小棒”解决退位减法，无论是从个位拿起还是从十位拿起，都是一样方便的。但是竖式是计算过程和结果的表达，把操作的过程抽象成竖式，并用它来理解竖式过程中每一步的含义，这是操作的目的。所以本环节设计跟学生一起经历记录操作的过程，使学生体会竖式的形成过程。在整个过程中，学生自然而然发现“列竖式计算时，从个位算起比较方便”。不用过多的语言强调，对比书写的过程就能显而易见。

2.解读竖式，对应算理。

同桌交流，相互提问：你是不是真的看懂了这个竖式？为什么退“1”？退“1”后个位怎么变？变成（）－8=（）？

3.分析错例，规范书写。

（1）分析错例1，认识退位点。

这个小朋友怎么算成28了呢？哪儿出问题了？有没有更简便的方法可以让大家记住从十位退下了1？

课件出示退位点：退位点表示什么意思呢？（表示十位少了1，个位多了10）

（2）分析错例2，个位6-8不够减，能倒着减吗？个位不够减，应该怎么办呢？

（3）规范书写，看来大家都会算了，让我们一起合作在黑板上完整地算一遍，好吗？你们指挥，我来写！（教师板演竖式计算过程）

（五）多元表征，理解算理。

1.小棒、竖式、计数器多元表征。

师：（课件出示算式50-26）你们会用小棒演示计算过程吗？用计数器呢？用竖式呢？

2.对比多元表征，感悟“退一作十”。

出示课件（如图5），比较三者表征，感悟“退一作十”。

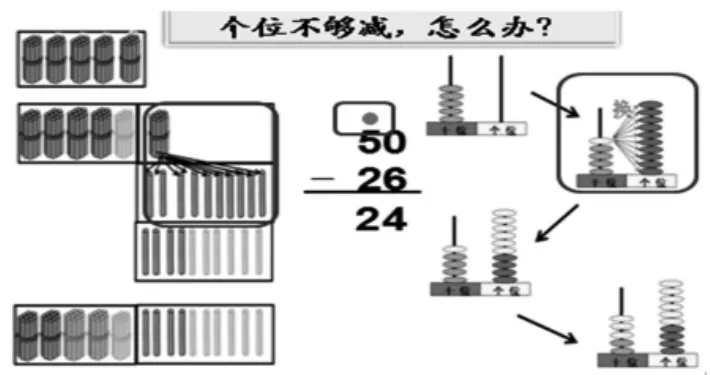
图5

小结：摆小棒时我们从5捆中退来1捆打散，用计数器时我们把十位上的1颗珠子换成个位上的10颗珠子，在竖式上我们用退位点表示十位少了1，个位多了10，在数学上把这种方法叫作“退一作十”，退的是十位上的“1”，作的是个位上的“10”。

【评析】小棒、计数器、竖式是退位减法的不同表达形式，抽象的程度也是不同的。抓“退位”这个核心，从多角度为抽象的“退位点”寻求丰富的表象支撑，实现从具象到符号的抽象。

（六）巩固练习，课堂小结。

第一关：把意义相同的用线连起来（如图6）。

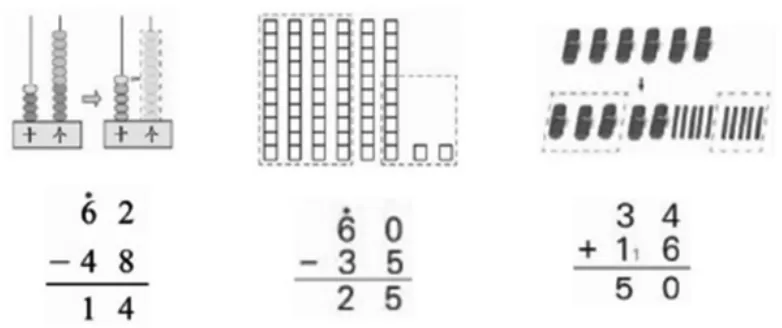
图6

第二关：猜一猜，方框后面都藏着几呀（如图7）？你是怎么猜的？

图7

图8

得数小于50可以填什么数？只要符合什么条件就可以了？得数不小于50可以填什么数？只要符合什么条件就可以了？

三、全课点评

在笔算教学中，我们会注重算法从学生中来，注重让学生亲历算法的思考过程，注重学生的动手操作。但由于笔算是“直观的算理，抽象的算法”，若不能沟通学具操作、口算与竖式表示的笔算之间的联系，尤其是将直观的学具操作转化为头脑中的表象，学生就难以真正掌握算法，理解算理。基于这样的思考，这节课的设计紧紧抓住了两个“借助”，在算法和算理之间形成了“无缝对接”的和谐统一。

（一）借助直观操作和多元表征，促进对算理的“真理解”。

学生的已有经验中更多的是“操作是操作，竖式是竖式”，这两者是脱节的，学生借助“学具操作”无法自主实现用“几何直观”解决数学问题的跨越。看来对于学生而言，理解算理，构建算法注定是一个艰难跋涉的过程，而不是简单的模仿。

这节课在笔算模型形成的过程中，始终借助摆小棒操作支撑每一步形成的过程，“为什么要借1捆？”“借来后干什么？”“借后发生了怎样的变化？”这三个问题的思考过程就是退位减法算法形成的过程，在这样的基础上将操作和竖式计算的每一步进行思维层面的一一对应，不但让学生理解了算理，还自然地形成了算法。

整节课通过“摆、拨、说、想、算”这样的多种语言表征形式，为学生在算法和算理之间搭起了一座桥梁，尊重学生，因势利导，从而促进了对算理的“真正理解”，促进笔算模型的产生、形成。

（二）借助操作流程的符号化，促进对“从个位算起”的“真知道”。

整节课借助小棒把抽象的算理直观化，在操作时发现不管是“从个位拿起”还是“从十位拿起”都一样方便。为什么竖式计算要从个位开始减起呢？教学不能仅仅是简单地告之学生，这节课通过把两种不同的拿小棒的过程用竖式表示出来，让学生体会到十位需要擦掉再改写比较麻烦，让学生感悟到在退位减法的竖式计算过程中从个位减起比较方便，做到了教学上的“润物细无声”。

在教学退位点时，在操作的基础上教师的及时追问促使学生深入思考。如：“退位点表示什么？在小棒图的哪里？在计数器的哪里？”归纳后继续追问：“退的是哪里的一？作的是哪里的十？”让学生理解“退一作十”的真正含义，也顺利地达成了从操作表征到符号表征的转化，让学生真正理解了“退位点”所包含的意义。

借助直观结构化材料学习计算并理解算理，最终应达到算法的熟练运用，这是一个长期的行为，而不仅仅只是第一课时中的“一次性”行为，这就要求我们在以后的计算教学中，处理好“算理直观和算法抽象”之间的过渡。

（本文作者系朱乐平数学名师工作站“一课研究”组成员，工作单位：浙江永嘉县桥头镇第二小学，浙江永嘉县教师发展中心）