实践出真知运用育素养——“不可思议的结果”教学案例及评析

◇设计、评析/汪学军 执教/张茜

实践出真知运用育素养
——“不可思议的结果”教学案例及评析

◇设计、评析/汪学军 执教/张茜

一提出问题

师：上课前，老师给大家发了一张报纸。假设一张纸的面积足够大。它的厚度是0.1毫米，如果将这张纸对折30次，将有多厚呢？

评析：本节课的主要目标是制订解决问题的方案，所以开门见山呈现问题，而不是基于情境让学生“发现提出问题”。

二理解问题

师：有多厚呢？谁来猜一猜？

生：它的厚度将会是3厘米。

生：6厘米。

生：我认为是4厘米。

师：也可以用手比画一下。

生:我觉得是5厘米。

生:原来是0.1毫米的话，乘以60，就是6毫米。（其他学生小声发出异议，停顿了一会儿）应该是6厘米。

评析：“猜一猜”活动引发了学生的运算结果与实际生活经验的冲突，激发了学生研究的需要，也使折30次到底是怎样的运算凸现出来。

三确定方案

师：同学们的答案都不一样，哪个答案是正确的，你打算怎样验证？

（学生没有反应）

师：你打算第一步做什么？第二步做什么？

（还是没有学生举手，教师直接点了一个学生）

生1:先拿一张纸，对折几次，发现其中的规律，就知道对折30次的厚度是多少了。

（其他学生疑惑地看着生1）

师：你还能发现其中的规律？

（教师本来希望学生说测量的，显然没有想到学生会这么回答）

师：哦，请坐！还有没有不同的想法？

生2：用0.1乘2，再乘2，一直乘30次就行了。

（生2说完后，此种方法并没有引起其他学生的注意和共鸣）

师：还有不同的想法吗？

生3：对折30次，然后再来测量。

（师板书：1.对折30次。2.测量）

评析：在最合理、最好的方案没有得到同学的理解和认可时，教师从学生认可但行不通的方案入手，顺应了学生认知的起点，曲折迂回的教学策略有利于学生积累数学活动经验。

师：拿出我们的报纸，折一折，量一量。

（生开始对折，折了七八次，就发现对折不了）

师：既然对折不了30次，我们也就无法测量。也就是说我们这个解决问题的步骤实现不了。那么该怎么修改呢？

生1:先对折10次，然后再测量，最后乘3。

师：为什么乘3呢？

生1：因为我们对折不了30次，我们是对折0次，30除以10等于3，所以要乘以3。

生2:我觉得应该对折5次。因为我刚刚折的时候，最多只能折7次，折不了10次，所以我选择对折5次。

生1:我同意生2的意见。

师：对折5次后，你打算怎么做？

生2:再用尺子测量，测量的厚度乘6，就是对折30次的厚度。

师：为什么要乘6？

生2：因为折30次的厚度是折5次的6倍，所以要乘6。

生3：老师，我想对折3次，再乘10。

师：刚才三名同学都说要将30这个次数减少。看来我们第一步就是对折较少的次数，那么对折几次呢？

生：3次、5次、6次都可以。

师：接着呢？

生：测量。

生：乘以倍数。

师：无论是对折3次、5次，还是6次，都要找与30次之间的关系。

（生回答，教师相机板书后，接着教师指着新拟定的解决问题步骤说：这就是我们修改后的解决问题的步骤，你们同意吗）

（师板书：1.对折较少的次数。2.测量。3.找与0次的关系。4.计算）

评析：什么样的解决问题的方案是有价值的？面对一个问题，能够顺利地拟订出解决问题的步骤固然是可喜的。如果从积累解决问题的数学活动经验来讲，让学生经历方案“失败——反思——修改”的过程更有价值。

四实施方案

师：老师还有一个问题想问问大家，我们如何研究对折5次和对折30次之间的厚度的关系？是直接量，还是用张数来分析？

生1：用张数分析。

生2：用量来分析。

生3：用张数来分析，测量有误差，再说也对折不了30次。

师：你打算如何记录对折后的张数？

生1：先写对折1次，再写多少张；接着写对折2次，再写多少张……就这样一直记录下去。

师：其实你是打算用表格记录，对吗？

师：像这样用表格记录的方法，有利于发现规律。

（出示表1和活动要求）

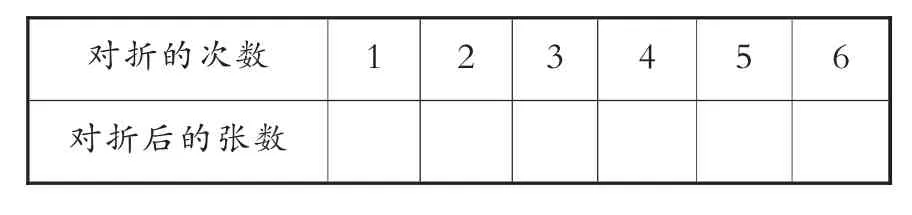
表1

活动要求：1.请同学们将每次对折后的张数填到表格中。2.观察表格，每次对折后的张数有什么规律吗？

（学生拿出教师提供的记录单，一边折，一边观察和记录。等学生活动完了，教师请学生汇报）

生1:对折1次的张数是2，对折2次的张数是4……对折6次的张数是64。

（生说完，教师用幻灯片出示下面的表格，如表2，接着问生1：最后一个64你是折出来的吗）

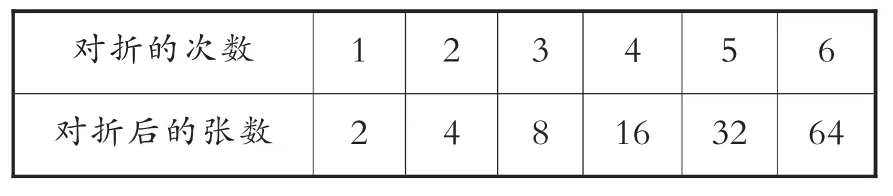
表2

生1:不是，是算出来的。

师：你怎么算的？

生1:第一次是2，第二次是4，第三次是8。2 乘2等于4，4乘2等于8，后面是8乘2等于16，16乘2等于32。每次乘2就等于下一次的张数。所以，对折6次的张数就是32乘2得64。

师：同学们，你们认为呢？

生2：张数是依次乘2，也就是前一次的张数乘2就是后一次的张数。

（师板书：前一次的张数×2=后一次的张数）

师：下面不再折纸，你能不能找到对折30次后的张数？

[师出示对折7～30次的表格（仿表，略）后，说：请继续写下去]

（生拿出计算器开始计算，并填在表格中）

师：对折30次后，一共是多少张呢？

（生数了数数，才回答道：十亿七千三百七十四万一千八百二十四张）

师：看到这个结果，你觉得——

生：太不可思议了！

（教师板书课题：不可思议的结果）

师：一张纸才0.1毫米厚，1073741824张纸到底有多厚呢？赶快在你的答题卡中写出来。

[等学生换算完后，教师展示一个学生的答题卡：1073741824×0.1=107374182.4（毫米）= 107374.1824（米）]

评析：不少老师反映综合与实践活动难以落实有以下两个原因：一是学习材料难准备；二是知识难度大，活动过程繁杂。本节课，首先学习材料只需要废报纸、计算器、作业纸，很好准备。其次，问题的主干文字少，简单明了。知识点只需小数的乘法、单位换算和估算，都不难。再次，这节课的过程清晰简单，没有在发现和提出问题、分析和解决问题各环节同时设置高难度的问题，而是选择一个侧重点。最后，整个探究的过程，让学生经历了模型的建立过程和运用模型解决问题的过程，发展了学生的核心素养。

五活动结论

师：107374.1824米到底有多厚呢？你们知道吗？

（生摇摇头）

师：世界上最高的山峰是珠穆朗玛峰，它的高度是8844.43米。估一估，对折30次的纸的厚度大约是几个珠穆朗玛峰的高度？

生1：大约是11个珠穆朗玛峰的高度，因为10万里面大约有10个，7374差不多又是1个，所以至少有11个珠穆朗玛峰那么高！

生2:大约是12个，把107374.1824米看作108000米，把8844.43米看作9000米，108000÷ 9000=12。所以对折30次的纸的厚度大约是12个珠穆朗玛峰那么高！

师：同学们，无论是11个，还是12个，想想我们原来估计的3厘米、5厘米、6厘米，这样的结果——

生：太不可思议了。

评析：将数量与一个具体形象的事物进行比较，使数学结论在学生脑海里变得具体形象，在估计的过程中发展了学生的数感。

六反思评价

师：光知道不可思议可不行，我们一起来回忆一下，在我们研究过程中遇到了什么困难？我们怎么解决的？

生：对折不了30次，我们就对折较少的次数，再来找规律。

师：将对折30次变成对折6次，再来找规律，这种研究方法在数学里叫化繁为简。同学们再看看，解决问题的步骤中，哪一步是找规律呢？

生：找与对折30次的关系就是找规律。

师：我们是怎样找规律的？

生：列一个表格，记录下来，再观察，就发现了。

师：很好！这就是列表的策略。大家再想一想，第二步测量用了吗？（学生都认为没有）我们用什么代替呢？

生：数张数。

师：所以我们解决问题的步骤还是四步。同学们，将来我们在解决问题的时候，经常会遇到一些意想不到的困难，我们要学会合理地调整解决问题的步骤和方法。

评析：对研究过程进行回忆反思起到了这样几个作用。一是通过回忆解决问题方案在实践操作中的落实过程，进一步反思方案的合理性，为今后的研究性学习积累有益的经验。二是回忆解决问题过程中策略的使用，为今后的合理应用策略积累经验。三是提炼活动中的数学思想方法，能为运用数学思想方法指导研究性学习打下基础。

（作者单位：湖北武汉市光谷九峰第一小学，武汉市光谷第九小学）