用幂级数研究常数项级数

◎聂 涛

(南京科技职业学院，江苏 南京 210048)

用幂级数研究常数项级数

◎聂 涛

(南京科技职业学院，江苏 南京 210048)

幂级数是最简单也是最重要的函数项级数，它在表示函数、研究函数性质及进行数值计算等方面都具有重要作用，同时它在研究常数项级数的性质方面也有重要的贡献.本文通过举例阐述了如何用幂级数判断常数项级数的敛散性并进一步求和.

幂级数；常数项级数；敛散性；和函数

一、用幂级数判断数项级数的敛散性

判断数项级数敛散性的方法有很多.有的数项级数可以用定义法，即通过求解部分和数列{Sn}的极限来判断；有的可以运用数项级数的性质来判断.对于正项级数，又有很多不同的判断方法，例如比较判别法、比值判别法、积分判别法、对数判别法、高斯判别法等等.还有交错级数的莱布尼兹判别法.

对于某些数项级数，这些方法都无法判断其敛散性，而通过幂级数展开式可以将原级数化成比较容易判断其敛散性的正项级数、交错级数或任意项级数.下面先给出莱布尼兹定理的推论.

分析 这是一个交错级数，无法用莱布尼兹定理判断其收敛性，数项级数的性质也不能用，而将通项取绝对值之后也无法用正项级数的审敛法判断，考虑到通项中函数的特点，可以用幂级数展开化简.

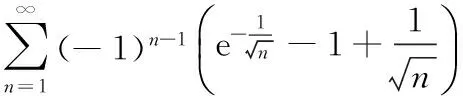
二、用幂级数求收敛的数项级数的和

一个收敛的数项级数的和就等于它的部分和数列的极限值，而对于部分和不可求或难以求解的数项级数，可以构造一个幂级数，求出它的和函数，然后求该和函数在某一点处的函数值.