广义不变凸函数多目标规划的对偶性

◎雷 鸣 李文钰 姜元政

(北华大学数学与统计学院，吉林 吉林 132013)

广义不变凸函数多目标规划的对偶性

◎雷 鸣 李文钰 姜元政

(北华大学数学与统计学院，吉林 吉林 132013)

本文讨论了不变广义凸函数多目标规划的对偶理论,弱对偶,直接对偶和逆对偶定理.将文[1]，[2]的结果给予推广.

不变广义凸函数；多目标规划；对偶理论

【项目】吉林省教育厅“十二五”科学技术研究项目：吉教科合字[2015]第133号.

一、引 言

多目标规划的对偶理论在多目标规划理论中占有重要的地位,它对多目标最优化问题中的求解以及最优性条件的揭示中都起到重要的作用.因此,好多学者都在不断地进行深入的研究.

本文讨论了如下形式的多目标规划(VP)和其对偶规划(VD)的对偶理论.

其中x∈En,f(x),g(x)和h(x)分别为p维、m维和s维的向量函数.≪uΤg(x)+vΤh(x)≫表示每个分量都是uΤg(y)+vΤh(y)的p维向量函数u∈Ep,v∈Es,λ∈Ep称(VD)为(VP)的Lagrange对偶问题.

文献[1]和文献[2]分别讨论了伪凸和拟凸多目标规划的对偶理论.本文就不变凸函数的一般情况给出了它的对偶理论.从而推广了文[1]，[2]的结果.

二、定义与引理

记P={x|x∈En,g(x)≤0,h(x)=0,x≥0},称P为多目标规划(VP)的可行域.

D={w|w=(y,u,v),u≥0,λΤf(y)+uΤg(y)+vΤh(y)=0}为(VD)的可行域.

定义2 称F(x)是集合X⊂En上的次线性泛函,如果F(x)满足：

(1)正齐次性：对∀α≥0及x∈X,有F(αx)=αF(x)成立；

(2)次可加性：对∀x,y∈X,有F(x+y)≤F(x)+F(y)成立.

我们构造如下的单目标规划：

三、(VP)与(VD)的对偶理论

对于广义F-凸函数而言,原问题(VP)的对偶问题(VD)具有如下形式,仍将其记为(VD).其可行域仍记为D,即

定理1 (弱对偶定理)若存在次线性泛函F(x),使f(x),g(x),±h(x)的每个分量函数都是P上的关于F(x)的F-凸函数.则对任意的x∈P,w=(y,u,v)∈D及λ∈Λ+,都有λTf(x)≥λG(y,u,v)成立.

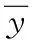
不难证明,在定理1,2,3中将F-凸函数分别换成F-拟凸和F-伪凸函数时,则各定理仍然成立.即(VP)与(VD)之间关于有效解仍是对偶的.在此不予重述.

[1]林锉云.多目标非线性规划的对偶理论[J].高等学校计算数学学报，1981,3(1):18-26.

[2]林锉云.多目标广义凸规划对偶理论[J].江西大学学报，1988，3(3)：3-13.

[3]MAHanson.OnSufficiencyoftheKuhn-Tuckercomditious.J.Math.Anal[J].1981，80(2)：545-550.