基于同伴教育设计学生“好学”的导学案的几点思考

唐婷颖　孙雅琴

摘 要：我国的新课程改革倡导把学生当成课程建设的主体，并以学生为中心建立自主、合作、探究的学习模式。因为人们通常愿意听取年龄相仿、知识背景、兴趣爱好相近的同伴、朋友的意见和建议，青少年尤其如此。利用青少年的趋众倾向，对青少年进行教育的方式，它符合青少年的心理，所以我校提出并实施了“自主学习，同伴教育”的课堂教学模式。而保障“自主学习，同伴教育”的效果的关键因素之一就是设计好学生“好学”的导学案，帮助学生完成自学。

关键词：同伴教育；导学案；设计

中图分类号：G633.6 文献标识码：A 文章编号：1992-7711（2016）12-067-2

我校提出并实施了“自主学习，同伴教育”的课堂教学模式，首先对有影响力和号召力的学生（同伴教育者即每个组的行政组长、学科组长）进行有目的的培训，然后再由他们组织同伴教育也就是小组合作学习，教师的引导穿插在学生的同伴教育过程之中，通过充分发挥学生的主体作用而实现课堂教学的高质量，而保障“自主学习，同伴教育”的效果的关键元素之一就是设计好学生“好（hǎo）学”的导学案，帮助学生完成自学。下面结合《函数（第一课时）》一课导学案的设计，谈一下笔者的几点思考。

一、正确认识导学案，是设计“好学”导学案的基础

导学案和传统的教案是有区别的。它既是隐含教师主导作用的文本——“导案”，又是一个满足学生认知目标的文本——“学案”，也是一个培养学生学习能力的文本——“练案”，还是一个师生、生生情感交流、对话的有机载体，一个蕴含新教育理念的创新文体。因此在导学案的设计上就显得尤其重要，老师也一定要对导学案有一个正确的认识，足够的重视。

笔者认为对导学案的理解是这样的：“导”就是指导，导学案就像旅游时候的导游图，它带领学生从入口进入，随着我们的指导的标志牌，经过自己的努力和同学的帮助，可以自己找到最后的出口，完成课程的学习。“学”就是指导学案是为了方便学生学习而设计的，因为我们在制定导学案的时候，会将复杂的问题进行化解，大的问题化成小的问题，更有利于让学生一步步来解决。“案”就是一种方案，就是学生学习的一个方案。总的来说，导学案就是教师编制的用于引导学生自主学习、自主探究的学习方案。

二、明确学习目标，是设计“好学”导学案的前提

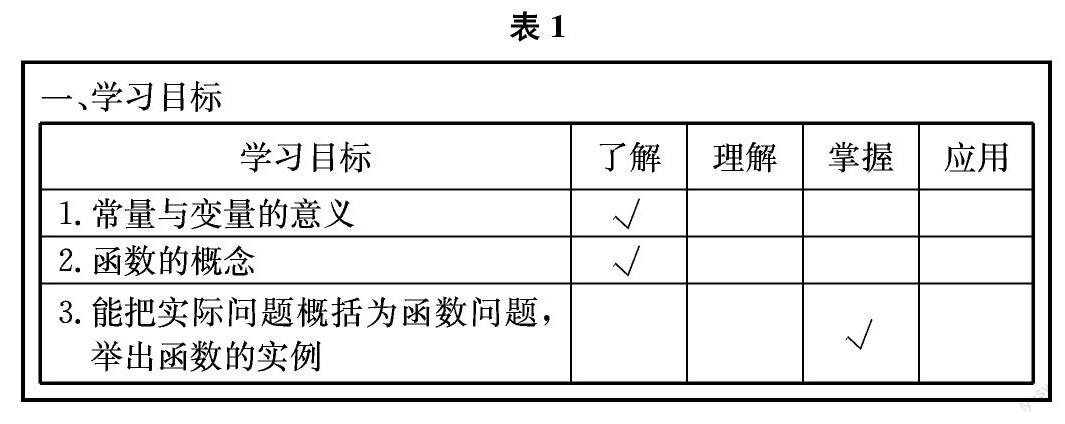
为了配合“自主学习，同伴教育”的课堂教学模式，我们的数学导学案分成“学习目标”、“问题导学”、“典例训练”、“拓展提升”、“达标测试”五个部分。明确“学习目标”，即要让学生了解本节课要学会什么，是设计“好学”导学案的前提。下表1是《6.1 函数（第一课时）》的学习目标，通过浏览这个表格，学生可以知道，本节课要学的是常量、变量、函数三个概念、同时能把实际问题概括为函数问题，很明显这就为学生明确了学习的方向。

三、合理设计“问题导学”，是设计“好学”导学案的核心

同伴教育（小組合作学习）的导学案是集“导”、“学”、“练”、“测”、“评”等功能于一体，是学生学习的路线图、指南针、导航仪，让学生学得舒服，让学生通过学习“好（hǎo）学”的导学案到“好（hào）学”数学。个人认为学案设计的核心应在“问题导学”部分上，设计上一般应根据学生认知规律，将知识点进行拆分、组合，设计成不同层次的问题，给学生一个自读、学习的思想导引，在遵循学案自学过程中，指导学生怎样思考、怎样操作，从而做出培养学生能力的具体设计，并在学习过程中潜移默化地培养学生的能力。因此，学案的问题导学部分的编写应注意关注学生水平，顾及不同层次学生；创设开放性问题，留下创新空间；链接生活和社会热点，培养学习能力。

1.问题设计层次化。

导学案的设计要遵循学生的学习规律，按照学生的学习全过程设计，层层递进的设计问题，将学生的重心前移，在课前自主学习时，在导学案的引导下，很“好学”，同伴教育的基础上实现教与学的最佳结合。如下表2中是《函数（第一课时）》的问题导学的问题一，通过两个常见的行程问题和费用问题，感悟归纳出常量与变量的概念。

《函数（第一课时）》的问题导学的问题二，就是在问题一的基础上，开始探究两个变量之间的关系，如下表3。第1、2、3题通过实际问题，引导学生通过自学，感受函数概念的一些要素，（1）在一个变化过程中，（2）有两个变量，（3）当一个变量变化时，另一个变量也随之发生变化，（3）当一个变量确定时，另一个变量也随之确定。特别是第3题在第1、2题的基础上，让学生模仿第2题中第（3）问的说法，描述本问题，层层深入的让学生感受刚刚所说的函数概念的3个要素。

为了突破函数概念中的一个难点，就是一个唯一性。即对于每一个x的值，y都有唯一的值与它对应。设计了下表4中的数字游戏，让学生体验每输入一个x的值，y都有唯一的值输出。在课堂教学时，教师可以设计一个课件，每输一个x，都对应得出一个y，和学生算的进行比对。进而，让学生归纳出，这是在一个变化过程中，有两个变量x和y，y随着x的变化而变化，对于每一个x的值，y都有唯一的值与它对应。函数的概念水到渠成，所有要素都可以由学生通过导学案的问题导学，感悟得出。

2.问题设计探究化。

学生通过探究性问题的学习和研究，要达到构建知识，掌握解决问题的方法，以及经历探究过程获得层次的情感体验和能力发展，因此一些封闭性的问题可以开放性的设计。比如表4中的数字游戏，设计成“请选择你喜欢的一个数作为x的值代入计算y”。这样一个开放性问题，一来学生感兴趣，二来在小组讨论时，更能让学生体验到，对于不同x的值，y都是有唯一的值与它对应的。为函数概念的得出，做了充分的铺垫。

3.问题设计情境化。

对于数学这个科目来说，因为学习的知识很多是比较抽象的，抽象的数学源于生活，来自具体，生活中处处有数学，学习数学就是为了解释和解决生活中的问题。因此，数学教学应开拓问题情境的时间和空间，我们的同伴教育已经将自主学习带到课外，带入一个新的起点。

《函数（第一课时）》中的“问题导学”的所有问题，都设计了生活化的情境。因为这种问题情境比较贴近学生的生活经验，经过思维碰撞之后，大多学生能探索出常量、变量及函数的概念。学生亲身经历了将实际问题抽象成数学模型并进行解释与应用的过程，自然而然地完成了函数概念的建构，也加深了对函数概念的理解，避免了死记硬背。而开放的问题情境，更是发展了求异思维、创造意识和解决问题的能力。因此很多内容学生不好理解，所以如果把问题的设计情境化，更有利于帮助学生去理解。

总之，让学生“好学”的导学案，“问题导学”部分必须精心设计，让学生在完成导学案的这部分内容时，顺利地完成新知识的建构。当然，导学案的其他部分的设计也是很重要的，例题必须精选，拓展提升必须找准拓展点，达标测试必须是和本课目标对接等。

[参考文献]

[1]李玉琪著.中学数学教学与实践研究.高等教育出版社，2012（07）.

[2]张奠宙，何文忠编.交流与合作.南宁：广西教育出版社，2009（01）.