集装箱港口连续泊位与岸桥的动态配置

梁承姬，夏 桑，鲁 渤

(1.上海海事大学 科学研究院物流研究中心，上海 201306；2. 中国科学院大学 管理学院，北京 100190)

集装箱港口连续泊位与岸桥的动态配置

梁承姬1，夏 桑1，鲁 渤2

(1.上海海事大学 科学研究院物流研究中心，上海 201306；2. 中国科学院大学 管理学院，北京 100190)

为缓解集装箱港口的泊位和岸桥资源比较紧张的现实情况，提高港口的运营效率，针对港口中泊位和岸桥的联合分配问题，在基于泊位和岸桥数量随时间动态变化的条件下，综合考虑泊位的连续性和船舶的泊位偏好性，建立了一个以船舶剩余作业量、船舶偏离偏好泊位的距离和岸桥移动次数之和最小为目标的混合整数线性规划模型，在保证船舶能在最迟离港时间前离港的前提下，让船舶尽快离港。通过CPLEX求解出此模型的最优解和算例分析，证实了文中的混合整数模型在解决实际港口中泊位和岸桥联合分配问题上的有效性。

交通运输工程；连续泊位；偏好泊位；岸桥动态分配；剩余作业量；混合整数线性规划模型

0 引 言

集装箱港口作为远洋运输、内河船舶运输以及内陆运输的关键枢纽，对于全球货物运输至关重要。2013年全球海运贸易量的增速整体好于世界贸易量的增速，同比增长4.81%，其中全球集装箱的海运量就达到1.60亿TEU，同比增长4.77%。随着经济的逐步复苏，集装箱港口的装卸需求量将会越来越大，但是集装箱港口的泊位本身受到自然空间与资源的限制，且岸桥是港口最为昂贵的作业设备之一，所以泊位和岸桥现已成为制约集装箱港口作业效率的主要瓶颈。集装箱港口迫切需要提高码头的泊位和岸桥的使用效率以减少船舶在港时间，使得港口的整体运营效率得到提高，才能更好地满足客户需求，提升港口的整体服务水平和竞争力。

泊位分配问题(berth allocation problem, BAP)和岸桥分配问题(quay crane assignment problem, QCAP)一直是集装箱港口优化生产运营的基础问题和热点问题，吸引了大量的学者研究。

根据对这两个问题的求解方法，现有研究可以分成两大类：第一类独立分配方法，即将这两个问题独立分开求解。K．H．KIM等[1]提出了基于一种惩罚策略的以费用最小为目标的泊位动态分配模型，并利用模拟退火算法进行了求解；R．TAVAKKOLI-MOGHADDAMA等[2]针对静态的岸桥分配与调度问题建立了混合整数规划模型，并设计了遗传算法求解；LU Zhiqiang等[3]研究了基于连续贝位的岸桥调度问题，将贝位划分为连续和不连续的集合，考虑岸桥冲突和阻塞，并利用启发式算法求解得到岸桥任务分配和序列。

BAP中的船舶作业时间直接与分配给船舶的岸桥数量有关，反之QCAP中已知的靠离泊时间是BAP的结果，所以这两个问题是相互影响相互决定的。考虑到BAP和QCAP之间的关系，学者开始关注第二类集成分配方法。Y．M．PARK等[4]考虑到各种现实的约束条件建立了整数规划模型，并将问题的求解分为两个阶段，第一阶段运用次梯度优化方法获得靠泊位置和时间以及配置的岸桥数，第二阶段运用动态规划方法求解岸桥的具体调度；靳志宏等[5]在泊位计划已知的前提下，考虑了避免岸桥交叉作业、作业任务的顺序要求等约束条件下的岸桥动态调度问题，构建了非线性数学规划模型，并用遗传算法进行求解；M．FRANK等[6]利用岸桥的效率表示船舶的处理时间，对泊位和岸桥的联合分配问题进行研究；LIANG Chengji等[7]建立了一个使得船舶的作业时间。等待时间和延迟时间最小的优化模型，并采用基于岸桥移动策略的混合遗传算法进行求解；高超锋等[8]也考虑了船舶的提早靠泊、推迟靠泊、延迟离港和偏离最佳泊位而引起的惩罚成本，并以总在港惩罚成本最小为优化目标建立了数学模型，并考虑岸桥并行作业效率约束，但其没有考虑岸桥的动态变化；林庆福等[9]先建立泊位岸桥集成分派混合整数规划模型得到初始分配调度方案，然后利用分层调整策略对方案执行过程中的干扰事件进行处理；韩俊等[10]研究了泊位与岸桥的协调调度问题，并利用免疫遗传算法对联合调度模型进行求解，但是其考虑的是离散泊位，而且没有考虑岸桥数量的动态变化；靳志宏等[11]研究了泊位分配计划和动态岸桥调度，将岸桥分为固定岸桥和移动岸桥这两个子集，建立了动态调度模型，并设计了遗传算法来求解该问题；CHANG Daofang等[12]建立了一个船舶的实际靠泊位置和偏好泊位的总偏离最小，延迟停泊惩罚成本和晚离港惩罚成本之和最小以及岸桥的总能量消耗量最小的多目标模型，并提出一种混合平行遗传算法进行求解；杨春霞等[13]建立了以最小化船舶在港时间和码头生产成本为目标的优化模型，并采用多目标遗传算法来求解，应用Pareto分级方法进行适应度值评价得到最终实施方案。

目前对于综合考虑泊位的连续性、偏好性和岸桥动态的联合调度的研究较少。笔者对到港的船舶进行泊位和岸桥的联合动态分配的问题进行了研究。不仅考虑了连续泊位和船舶的偏好靠泊位置，而且给船舶分配的岸桥数量是随着时间动态变化，充分利用有限的岸桥资源完成船舶任务，同时为减少岸桥的能源消耗；笔者还考虑了尽量减少岸桥的移动次数，使船舶尽量以一个较为理想的状态离港。此外，笔者对泊位和岸桥进行联合分配的方法充分考虑了BAP和QCAP之间相互影响相互制约的关系，避免了作业的一些冲突，更符合码头生产组织的实际情况。

1 问题描述

在船舶实际到港之前，港口就需要根据船期表(即包括船舶的名称、预计到港时间和装卸量等信息的表格)确定计划周期内船舶的靠泊时间和位置，还有分配给船舶的岸桥数量。将连续岸线划分为1 m的连续小单位，从左到右递增，并且将一个工作日划分为24个时间段，每个时间段为1 h。

船舶实际在港口靠泊时，基于安全考虑会在船的前后都预留船长10%的距离，实际占用岸线长度包括船长和预留10%船长的泊位安全距离，如图1。

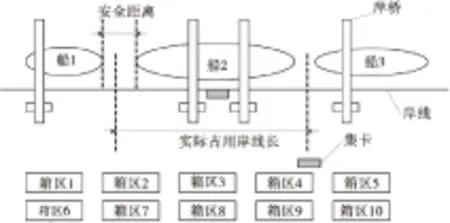
图1 集装箱港口岸边作业示意Fig.1 The operation of container terminal in quayside

由于港口对堆场箱区进行了分类，所以基于使集卡在堆场至岸边的运送距离最短的原则，每条船舶都会有一个偏好的靠泊位置，这在确定泊位计划时需要考虑进去；如果船舶实际靠泊的位置偏离了偏好泊位，则使得船舶上每个集装箱的运输路径都增加，这就会增加集装箱的运输成本。岸桥可以沿着轨道在岸边移动，也就使得在港口实际运营中分配给船舶的岸桥数量可以根据任务的完成情况和紧急程度而调整变化。岸桥卸载完船上的集装箱或者装完需要装船的集装箱后，船舶即可离港，而后面进来的船就可以停靠在空的泊位，所以泊位和船上的岸桥数量都是动态变化的。

笔者考虑到连续泊位，而且分配给船舶的岸桥数量可以随着时间动态变化，建立了以船舶剩余作业量、靠泊位置离偏好位置距离近和岸桥移动次数最小为目标的混合整数规划模型。以便确定船舶的泊位计划和每个时间段给船舶分配的岸桥数量更加贴近港口的实际生产情况。船舶的剩余作业量是船舶还未完成的任务量，船舶在进港时间段的初始剩余作业量是船舶总任务量。由于每条船舶有最大作业路，若船舶从进港时间段开始，港口就给船分配最大作业路数量的岸桥作业，即分配最大可能数量的岸桥给船舶，那么船舶会产生一个最早离港时间。若船舶能按照最早离港时间离港，则称这条船舶的作业达到了一个理想状态。但是，实际的港口中由于有限的泊位和岸桥资源，大多数的船舶都不能达到这种理想状态。若有一条最大作业路为4，任务量为700 TEU的船舶在第1时间段进港，每台岸桥作业速度为50 TEU/时间段，那么700/(50×4)得出其到第4个时间段就能完成所有任务，该船舶最早能在第4个时间段完成作业，这是船舶作业的理想状态。实际上若给船前3个时间段都分配4台岸桥，第4个时间段分配2台岸桥完成剩余作业量，则船舶也能在第4个时间段就完成任务，作业也能达到这种理想状态。若从第3时间段开始只给船舶分配2台岸桥，那么船舶就无法在第4个时间段完成作业，即图2中的非理想状态。还有一种情况是若第1时间段由于岸桥资源紧张给船舶只分配2台岸桥，第2，3，4时间段分配4台，船舶也能在第4时间段完成作业，但是这样为了让船舶作业达到理想状态而先减少再增加岸桥数量就增加了岸桥的移动。所以以最小剩余作业量为目标同时，还要考虑到岸桥增加的移动所带来的成本。

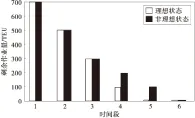
图2 剩余作业量的比较Fig.2 Comparison of remaining workload

2 混合整数线性规划模型

为解决港口泊位和岸桥的联合分配问题，笔者建立了一个混合整数线性规划模型进行求解。首先模型是基于如下假设：

1) 每台岸桥的装卸速度相同，即不同的岸桥作业同一个任务所需的作业时间相同，且岸桥在一个时间段中的作业不能中断；

2) 岸桥的移动时间以及岸桥之间的安全距离忽略不计，不考虑岸桥的移动范围；

3) 船舶进港和靠离泊的准备时间均忽略不计；

4) 每艘船都有最大作业路，即可同时作业的岸桥数的最大值。由于船只的长度有限，分配给每艘船作业的岸桥数量也有限制；

5) 每艘船都有并且只有一个最合适的停泊位置，即船舶的偏好位置。最合适位置是距离要装卸集装箱的存储箱区最近的岸线位置，同时可能也要考虑到这个位置的吃水深度和海浪的强度和方向。

2.1 参 数

T表示时间集合；t表示时间；I表示船舶集合；i表示船舶；Q为可用的岸桥总数；L为总岸线长度，即可用靠泊的位置总长；BLi为船舶i的偏好靠泊位置；Di为船舶i的最大作业路；li为船舶i靠泊时占用岸线的长度；Ni为船舶i上需要作业的总TEU数量；ATi为船舶i到港时间段；V为岸桥作业速度，TEU/台·时间段；MTi为船舶i最小服务时间，MTi=Ni/(Di·V)；ETi为船舶i最早离港时间，ETi=ATi+MTi；LTi为船舶i最晚离港时间；ω为增加移动岸桥的惩罚系数；α为船舶作业延迟的惩罚系数；β为偏离偏好泊位的惩罚系数。

2.2 决策变量

Xit表示若船舶i在t时间段有岸桥在作业，则其值为1，否则为0；nit表示t时间段分配给船舶i的岸桥数量；Cit表示相比于(t-1)时间段，t时间段分配给船舶i的岸桥数量的变化；Rit表示船舶i在t时间段初剩余的工作量；ALi表示船舶i的实际靠泊位置；DLi表示船舶i实际靠泊位置和偏好靠泊位置的偏差；yij表示若船舶i在船舶j左侧靠泊，则其值为1，否则为0。

2.3 目标函数和约束条件

minZ=

(1)

(2)

ALi+li≤L,∀i∈I

(3)

(4)

Xit+Xjt≤1+yij+yji,∀i,j∈I，且i≠j，∀t∈T

(5)

(6)

Ri,ATi=Ni,∀i∈I

(7)

(8)

Rit≥Ri,t-1-ni,t-1·V,∀i∈I,∀t=ATi+

1,…,LTi

(9)

Rit≤nit·V,∀i∈I,t=LTi

(10)

nit≤Di,∀i∈I,∀t=ATi,…,LTi

(11)

(12)

Cit≥nit-ni,t-1,∀i∈I,∀t=ATi+1,…,LTi

(13)

nit-Xit·M≤0,∀i∈I,∀t∈T

(14)

nit+(1-Xit)·M≥1,∀i∈I,∀t∈T

(15)

nit-Rit·M≤0,∀i∈I,∀t∈T

(16)

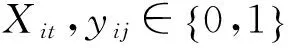
(17)

目标函数式(1)包括最小化3个部分：

第1个部分是最小化从船的最早离港时间前一个时间段至最迟离港时间的作业剩余量。在岸桥资源紧缺时，最小化剩余作业量能让船尽量接近船舶的理想状态，使得船舶尽快离港。在实际的港口中由于泊位和岸桥资源紧张等原因无法满足让每条船都按照最早离港时间离港，在作业上有一定的延迟，所以在前面加入了惩罚系数α。

第2部分是使船尽量靠泊在船的偏好靠泊位置。若船没有在偏好位置靠泊，则会使每个集装箱的运输路径增长，增加港口的运输成本，所以加入了惩罚系数β。

第3个部分是最小化岸桥的移动量。在实际港口中，岸桥移动量增加相应也会增加港口的时间成本，所以加入了惩罚系数ω。

式(2)～式(17)是约束条件。式(2)是定义决策变量DLi；式(3)保证船在靠泊时不会超过港口的岸线总长；式(4)是定义决策变量yij，若yij=1，则船舶i是停靠在船舶j的左侧；式(5)避免两条船在同一时间靠泊在同一位置的冲突；式(6)定义决策变量Xit和Rit之间的关系，保证船一旦开始作业，则要连续作业下去直到所有作业完成；式(7)定义每艘船的初始作业量；式(8)保证船在到港时间之前船的剩余作业量等于0；式(9)定义决策变量nit和Rit之间的关系，表示作业剩余量在经过一个时间段作业后的变化，并且保证作业剩余量不会减少到0以下；式(10)保证船能够在最迟离港时间之前离港；式(11)保证在每个时间段分配给船的岸桥数不超过船的最大作业路数；式(12)保证每个时间段分配给船的岸桥总数不超过可用的岸桥数量；式(13)定义决策变量Cit；式(14)和式(15)定义决策变量nit和Xit之间的关系；式(16)定义决策变量nit和Rit的关系；式(17)定义决策变量Xit，yij为0～1整数变量。

3 试验算例

为了验证上述模型的有效性，笔者采用上海市某国际集装箱港口的实际数据进行研究，并采用CPLEX优化软件进行求解。

3.1 输入数据

由于笔者不考虑驳船，所以根据该港口的数据，除去驳船作业区域占用岸线长度，该港口的实际可用岸线长度是1 300m，岸桥为15台，岸桥的作业速度取平均作业速度50TEU/h，移动岸桥的惩罚系数ω=150，船舶i作业延迟的惩罚系数α=10，偏离船舶i的偏好靠泊位置的惩罚系数β=0.000 4。

笔者考虑了该港口2014年某日的到港船舶，根据港口实际在船的前后都预留船长10%的安全距离的原则，实际占用岸线的长度是120%船长，可以计算得到船舶实际在港口占用的岸线长度；根据船舶的作业量、最大作业路和岸桥作业速度，可以通过公式MTi=Ni/(Di·V)求出最小服务时间，也可求出船的最早离港时间，其具体数据如表1。

表1 舶处理数据

3.2 结果分析

基于3.1小节数据计算的结果整理后如图3。在图3中，横坐标为岸线，即泊位资源，纵坐标为时间段。图3中不同深浅的矩阵表示不同的船，矩阵的宽度表示船占用的岸线长度；矩阵的长度表示船作业占用的时间段；矩阵中的数字表示每个时间段分配给船的岸桥数量，这个岸桥数量是随着时间段而变化的。矩阵左上角标有船号，各船的实际靠泊位置如表2。从图3中可以看到，进港的船舶基本能保证船舶在最迟离港时间之前离港。

由于船6在第3时间段进港而使得岸桥资源变得紧张，所以分配给船7的岸桥数量减少。从第6时间段开始，船4和船5这种更大的船进港后使得岸桥资源相对变得更加紧缺，所以刚开始给船3和船4分配的岸桥数量相对较少，随着船1作业即将完成逐渐减少了岸桥以便于船4和船5能有更多的岸桥可以使用。到第10个时间段船3进港靠泊后，此时岸桥资源依然紧张，给船3分配的岸桥只有4台。到第11时间段，船2的作业也即将完成，逐渐减少了岸桥。岸桥的这种动态更能充分利用港口有限的岸桥资源，提高港口的运营效率，更加符合港口的实际作业情况。同时可以看到在船1，2，4和5进港靠泊后，泊位资源也变得紧张，所以船3实际进港的时间延迟了2个时间段。通过比较表1的数据和实际靠泊位置，会发现有6艘船偏离了船的偏好位置，只有船1停靠在偏好泊位，船2，3，4偏离较少，船5，6，7偏离较多。作业的任务量、泊位冲突、进离港时间和船作业时间都会导致这种偏离差距的变化。比如船7由于船1泊位的占用，靠泊位置偏离了430 m，但船7的作业量相对较少，为了保证船舶7尽快离港，所以其靠泊位置偏离距离会大一些。

图3 船舶泊位和岸桥动态配置结果示意Fig.3 Dynamic allocation result of berthing location and quay crane of vessels表1 船舶靠泊位置结果Table 2 Result of vessels’ berthing location

船号1234567实际靠泊位置0964141724408408530

4 结 语

在一个24 h的计划周期内，多艘船舶先后抵达港口，根据船公司提前提供的进港时间、离港时间和船的作业量，如何安排多艘船的靠泊和根据时间段分配岸桥给船舶，是笔者解决的主要问题。

笔者建立了一个混合整数模型，在保证船舶能在最迟离港时间前离港的条件下，尽量让船舶尽快离港，同时充分考虑了船舶的偏好靠泊位置和岸桥移动增加的成本。根据上海某实际港口的数据，求出的最优解也验证了文中的混合整数模型解决港口泊位和岸桥动态配置问题的有效性。但是笔者没有考虑随机因素和其它作业机械的影响，此方面还有待进一步研究。

[1] KIM K H, MOON K C. Berth scheduling by simulated annealing[J].TransportationResearchPartB:Methodological,2003,37(6):541-560.

[2] TAVAKKOLI-MOGHADDAMA R, MAKUI A, SALAHI S, et al. An efficient algorithm for solving a new mathematical model for a quay crane scheduling problem in container ports[J].Computers&IndustrialEngineering,2009,56(1):241-248.

[3] LU Zhiqiang, HAN Xiaole, XI Lifeng, et al. A heuristic for the quay crane scheduling problem based on contiguous bay crane operations[J].Computers&OperationsResearch,2012,39(12) :2915-2928.

[4] PARK Y M, KIM K H. A scheduling method for berth and quay cranes[J].OperationResearchSpectrum,2003,25(1):1-23.

[5] 靳志宏，李娜.基于泊位计划的集装箱码头岸桥动态调度优化[J].交通运输系统工程与信息，2011，11(3)：59-64. JIN Zhihong, LI Na. Optimization of quay crane dynamic scheduling based on berth schedules in container terminal[J].JournalofTransportationSystemsEngineeringandInformationTechnology,2011,11(3):59-64.

[6] FRANK M, CHRISTIAN B. Heuristics for the integration of crane productivity in the berth allocation problem[J].TransportationResearchPartE:LogisticsandTransportationReview, 2009,45(1):196-209.

[7] LIANG Chengji, HUANG Youfang, YANG Yang. A quay crane dynamic scheduling problem by hybrid evolutionary algorithm for berth allocation planning[J].Computers&IndustrialEngineering,2009,56(3):1021-1028.

[8] 高超锋，胡志华.岸桥并行作业效率约束下泊位与岸桥集成分派[J].重庆交通大学学报(自然科学版)，2014,33(3):72-78. GAO Chaofeng, HU Zhihua. Berth-crane allocation constrained by parallel operation efficiency of quay cranes[J].JournalofChongqingJiaotongUniversity(NaturalScience),2014,33(3):72-78.

[9] 林庆福，胡志华，陶莎.集装箱码头泊位-岸桥集成分派干扰管理的分层调整策略[J].重庆交通大学学报(自然科学版)，2014,33(3):134-141. LIN Qingfu, HU Zhihua, TAO Sha. Multi-level adjustment strategy for disruption management of berth-crane allocation problem at container terminals[J].JournalofChongqingJiaotongUniversity(NaturalScience),2014,33(3):134-141.

[10] 韩骏，孙晓娜，靳志宏.集装箱码头泊位与岸桥协调调度优化[J].大连海事大学学报，2008,34(2):117-121. HAN Jun, SUN Xiaona, JIN Zhihong. Coordinated optimization method for berth and quay crane allocation in container terminal[J].JournalofDalianMaritimeUniversity,2008,34(2):117-121.

[11] 靳志宏，徐奇，韩骏，等.集装箱码头泊位与岸桥联合动态调度[J].中国科技论文在线，2011，6(11)：809-814. JIN Zhihong, XU Qi, HAN Jun, et al. United dynamic scheduling of berths and quay cranes in a container terminal with consideration of actual constraints[J].SciencePaperOnline,2011,6(11):809-814.

[12] CHANG Daofang, JIANG Zuhua, YAN Wei, et al. Integratingberth allocation and quay crane assignments[J].TransportationResearchPartE:LogisticsandTransportationReview,2010,46(6):975-990.

[13] 杨春霞，王诺.基于多目标遗传算法的集装箱码头泊位-岸桥分配问题研究[J].计算机应用研究，2010，27(5)：1720-1725. YANG Chunxia, WANG Nuo. Berth-quay crane allocation in container terminal based on multi-objective genetic algorithm[J].ApplicationResearchofComputers,2010,27(5):1720-1725.

The Dynamic Allocation of Continuous Berth and Quay Cranes in Container Terminals

LIANG Chengji1, XIA Sang1, LU Bo2

(1.Logistics Research Center, Shanghai Maritime University, Shanghai 201306,P.R.China； 2. School of Management, University of Chinese Academy of Sciences, Beijing 100190,P.R.China)

In order to mitigate the reality that berths and quay cranes were in short in container terminals, improve port operation efficiency and achieve collective assignment of berths and quay crane in ports, based on the time-dependent dynamic change of berth and quay crane quantity and after considering the continuity of berth and vessel berthing preferences one mixed integer linear programming model was established for the purpose of minimizing the sum of remaining workload of vessels, the distance between preference berth and the actual berth of vessels, the quay cranes’ shifting times. By this model vessel was allowed to depart as soon as possible ensuring vessel departure by latest allowable departure time. Then according to an actual port’s data in Shanghai, CPLEX was used to solve the model and an optimal solution was achieved. Finally, the computational result confirms the feasibility of this model in solving the joint allocation of berth and quay cranes in container terminals by analyzing the numerical example.

traffic and transportation engineering; continuous berth; preference berth; dynamic allocation of quay cranes; remaining workload; mixed integer linear programming model

10.3969/j.issn.1674-0696.2016.05.30

2014-12-31；

2015-03-14

国家自然科学基金资助项目(71471110；71301101)

梁承姬(1970—)，女(朝鲜族)，吉林龙井人，教授，博士，主要从事物流系统运作计划与优化、资源配置/分派优化与模拟、港口布局优化与模拟、口岸物流流程模拟与重组、港口安全工程方面的研究。E-mail:liangcj@shmtu.edu.cn。

夏 桑(1990—)，女，湖南衡阳人，硕士研究生，主要从事港口优化方面的研究。E-mail:xs0104@163.com。

U694

A

1674-0696(2016)05-155-05