服役RC梁桥CFRP板加固后的动态可靠度分析
陈 强
(湖南城市学院 土木工程学院,湖南 益阳 413000)
服役RC梁桥CFRP板加固后的动态可靠度分析
陈 强
(湖南城市学院 土木工程学院,湖南 益阳 413000)
建立起服役(RC)钢筋混凝土梁桥在(CFRP)碳纤维板加固前后正常使用状态下荷载效应的均值和标准差模型;采用模糊当量法将服役RC梁桥在正常使用极限状态的挠度当量转换为在一定区间内的均匀分布函数;在此基础上建立了服役RC梁桥在CFRP板加固后的正常使用极限状态方程。结合某座加固实体工程,采用JC验算点法计算了该桥在正常使用极限状态下,加固完成时及加固后的动态可靠度指标,得到了加固完成时可靠度指标的提高量及加固完成后可靠度指标的变化规律。研究发现:用CFRP板加固现有梁桥后,1号梁仍不能满足正常使用要求,2号梁在加固后服役30年后仍不能满足正常使用要求,说明目前采取碳纤维板加固桥梁在正常使用能力可靠性方面仍有所欠缺。
桥梁工程;服役RC梁桥;CFRP板加固;模糊当量法;JC验算点法;动态可靠度
随着交通量的日益增加,桥梁的服役环境不断恶化,桥梁往往达不到设计使用寿命,桥梁工程师通常采用维修加固来满足服役桥梁的承载能力及正常使用要求。目前针对服役桥梁加固前后在正常使用状态下的可靠度指标具体提升幅度,以及加固后续服役期内是否满足正常使用要求的研究还比较少。因此,有必要对服役RC(钢筋混凝土)梁桥在加固前后正常使用状态下的可靠度指标进行分析与计算。
刘伟强[1]通过将正常使用极限状态下的抗力当量为正态随机变量,计算分析了钢筋混凝土桥梁在裂缝和挠度两方面的可靠度指标,得出服役桥梁正常使用极限状态下的可靠度指标分布范围。赵羽习等[2]将混凝土构件的锈胀裂缝作为分析对象,计算了正常使用极限状态基于锈胀的可靠度指标。以钢筋锈胀力作为正常使用极限状态下的荷载效应,通过将混凝土保护层出现锈胀裂缝时的钢筋锈胀力作为抗力,建立正常使用极限状态方程。利用可靠度程序,计算了相对应的可靠度指标。最后讨论了各个因素对正常使用极限状态可靠度指标的影响。
采用模糊当量法,将服役RC梁桥正常使用状态下的挠度和裂缝宽度当量转换为一定区间内的均匀分布函数,建立了正常使用状态下基于挠度的荷载效应均值和标准值模型,并建立起正常使用状态下极限状态方程。采用JC验算点法编制了相应的计算程序,并计算了一座旧桥在加固完成时和加固后的动态可靠度指标。
1 桥梁挠度当量随机化
和承载能力状态下抗力不同,正常使用极限状态下抗力具有较强的不确定性,比如结构的挠度是工程师依据规范以及经验规定的,具有模糊不确定性,而且正常使用下的失效准则是模糊的,这使得功能函数Z只反映了结构适用性程度的大小。Z<0不代表结构完全失效;Z>0也不代表结构完全处于可靠状态;Z=0也不完全是结构极限状态。因此,需将结构裂缝宽度和挠度采用模糊当量法进行分析。
结构失效模糊随机事件可用式(1)表示:
E={[Z,μE(z)]|z∈Ω}
(1)
式中:z∈Ω为结构模糊随机事件空间中的随机变量。
假设功能函数Z的概率密度函数为fZ(z),那么结构失效事件E的概率为
Pf=∫-∞+∞μE(z)fZ(z)dz
(2)
式中:μE(z)为z的递减函数,随着z值的减小,结构的失效程度随之增大。
若基本随机变量X的概率密度函数为fX(x),那结构失效事件E的概率则可表示为
Pf=∫-∞+∞μE[gX(x)]fX(x)dx
(3)
将上述概念应用到结构功能函数,假设结构抗力和荷载效应是相互独立的,则有结构的失效概率为
Pf=∫0+∞∫0+∞fR(r)fS(s)μR(r,s)drds
(4)
式中:fR(r),fS(s)分别为抗力和荷载效应的概率密度函数;μR(r,s)为模糊随机失效事件的隶属函数。
由于工程结构中通常将的结构挠度作为一个限值来表示,故可将式(4)简化为式(5):
Pf=∫0+∞fS(s)μR(s)ds
(5)
将构件的失效作为模糊随机事件,其隶属函数一般通过模糊统计试验来确定,唐铁羽等[3]建议隶属函数取做升半梯形,其分布如下
(6)
式(6)的一阶导数为:
(7)
通过式(6)和式(7)可看出:隶属函数在区间[r1,r2]上服从均匀分布的概率分布函数和概率密度函数。故在正常使用极限状态下计算结构动态可靠度指标时,可采用将结构的模糊挠度当量随机化,比如使结构挠度当量成为在区间[W1,W2]上的均匀分布函数,其均值和标准差分别为
(8)
式中:W1和W2分别为限值。
《公路钢筋混凝土及预应力混凝土桥涵设计规范》[4]规定:钢筋混凝土和预应力混凝土受弯构件的长期挠度值,在扣除结构自重产生的长期挠度后,梁桥主梁的最大挠度限值为计算跨径的1/600;梁式桥主梁的悬臂端的最大挠度限值为悬臂长度的1/300。在计算基于挠度的正常使用极限状态下的动态可靠度时,可以取计算跨径的1/400作为抗力模糊失效上限,将计算跨径的1/800作为抗力模糊失效的下限。
2 基于跨中挠度的荷载效应
钢筋混凝土受弯构件正常使用极限状态下的挠度效应计算,可以依据规范给定的刚度计算公式,然后再依据结构力学的方法计算而得。《混凝土结构设计规范》[5]规定了混凝土受弯构件短期刚度计算公式:
(9)

CFRP板的换算等效钢筋截面积公式[6]为
(10)
式中:Ecf为CFRP板的弹性模量;Es为钢筋弹性模量;η为截面内力臂系数,η=0.87;h0为截面有效高度;as为受力钢筋合力点至最近截面边缘的距离;K为实际受压有效高度和有效高度的比值,K≈0.4;Acf为CFRP板截面积。
将CFRP板截面积等效为钢筋截面积,与随时间变化的锈蚀钢筋截面积相加,并代入式(11),可求其加固后的短期刚度。混凝土受弯构件考虑荷载长期作用影响的刚度Bl可按式(11)计算。
(11)
式中:Mk为按荷载标准组合计算出来的弯矩,Mk=MG+MQ,MG为恒载,MQ为活载;Mq为按荷载准永久组合计算出来的弯矩,Mq=MG+φMQ,φ为准永久组合系数,对于汽车荷载取效应φ=0.4;θ为荷载长期作用对挠度增大的影响系数,对于钢筋混凝土受弯构件,混凝土受压区配筋率为0时,取θ,当混凝土受压区配筋率等于受拉区配筋率时,取θ=0.2,当受压区配筋率为中间值时,θ按线性插值法取值。
简支梁跨中受弯挠度荷载效应为
(12)
式中:l0为计算跨径;Bl为荷载长期作用影响刚度。
挠度荷载效应的均值和标准差模型依据误差传导公式可分别推导出如下:
(13)
3 极限状态方程及目标可靠度指标
正常使用极限状态下挠度的极限状态方程可用下式表达:
Z=[f]-f*
(14)
式中:[f]为基于挠度的限值,同样在区间[f1,f2]上服从均匀分布;f*为基于挠度的荷载效应,f*=αf,α为挠度计算模式不定性系数,f*服从对数正态分布。
确定正常使用极限状态的目标可靠度指标本质上是确定一个可以接受的正常失效概率的协议概率Pf。依据李杨海等[7]的计算可知,正常使用极限状态下的失效概率Pf应在5%~25%之间,相应的目标可靠度指标βT应在0.675~1.645之间。当确定正常使用状态下的极限状态方程以及抗力和荷载效应的分布后,就可以利用JC当量随机正态法迭代求解正常使用极限状态下的可靠度指标[8]。
4 算例分析
某桥为T型普通钢筋混凝土简支梁桥,维修加固前的服役时间为50年。桥址处环境为RH=70%,温度T=20 ℃。桥梁全长100 m, 桥宽为7.0 m(车行道)+2×0.15 m(护栏),全桥共有5跨,每跨计算跨径为16.8 m,混凝土强度为C25,保护层厚度为30 mm,受拉主筋为4φ32和2φ16的钢筋,分3排布置,该桥原设计荷载为汽-15级,近年来由于公路运输发展较快,将其承载能力由原汽-15级提升至公路-II级。现将梁底黏贴1.2 mm的CFRP板加固处理,其弹性模量为165 000 MPa,极限拉伸强度为2 800 MPa。该桥横截面及尺寸如图1。
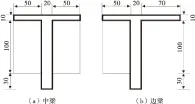

图1 横截面(单位:cm)Fig.1 Cross section
4.1 加固完成时可靠度指标的计算
基于李扬海等[7]的计算方法及计算结果,并将已知参数带入式(9),即可求得各梁短期刚度为表1。
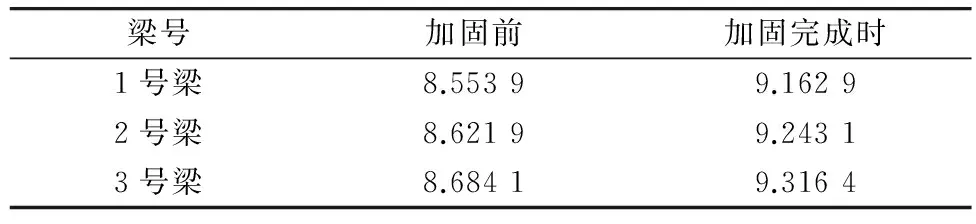
表1 各梁短期刚度值Bs
同样可求得各梁长期刚度如表2。

表2 各梁长期期刚度值Bl
(续表2)

梁号加固前加固完成时2号梁4.95475.31173号梁4.91915.2773
依据式(8),结合表2的参数,利用已知数据可求得各梁挠度的均值和标准差见表3。
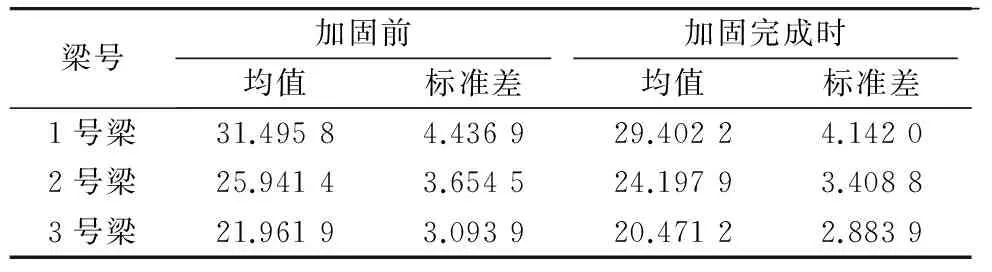
表3 各梁挠度均值和标准差
由式(13)可知, 挠度均值为28 mm,标准差为12.124 4 mm,结合正常使用极限状态方程,计算各梁正常使用极限可靠度指标如表4。

表4 各梁碳纤维加固完成时可靠度指标
由表4数据可知对于1号梁,CFRP板加固前及加固完成时都满足不了正常使用极限状态下对于可靠度指标区间在0.675~1.645的要求;2号梁在加固之前不能满足目标可靠度指标的要求,但在加固完成时能满足要求;3号梁在加固前和加固完成时都能满足目标可靠度指标的要求。表明对于1号梁还需采取增加其刚度的措施以减小其挠度。
1,2,3号梁可靠度指标提升量分别为0.224 4,0.240 9,0.302 5;3号梁其正常使用极限状态的可靠度指标提升得最多,3片梁的可靠度指标平均提高量为0.255 9。
4.2 加固后可靠度指标的计算
同样的方法可以计算出各个时间梁的可靠度指标如图2。

图2 CFRP板加固后1~3 号梁的可靠度指标Fig.2 Reliability index of the 1~3 # beams strengthened with CFRP sheets
由图2可知,CFRP加固后,在外界环境和车辆荷载作用下,各梁的正常使用可靠度指标均随时间的增加而降低。对1号梁而言,即使采用CFRP板加固,可靠度指标仍不能满足正常使用极限目标可靠度的要求,可以采取增大梁截面刚度的方法使得其可靠度指标满足正常使用极限状态目标可靠度指标的要求;2号梁采用CFRP板加固后可靠度虽然满足正常使用极限状态目标可靠度指标的要求,但是在大约在加固后服役30年(桥梁服役80年)后就不能满足目标可靠度指标的要求,也可适当的增大刚度;只有3号梁一直到桥梁服役100年都能满足正常使用极限状态目标可靠度指标的要求。
在后继可靠度指标下降趋势上,虽然加固后有15年初始钢筋锈蚀延缓期,但可靠度指标没有一个明显的缓慢下降的趋势。由图2可看出:各梁的可靠度指标相差较大,这是由于正常使用极限状态下基于挠度可靠度指标的计算只考虑了荷载效应中的汽车荷载,而没有考虑恒载效应。这种情况是由于我国《公路钢筋混凝土及预应力混凝土桥涵设计规范》规定:钢筋混凝土和预应力混凝土受弯构件的长期挠度限值是在在扣除结构自重产生的长期挠度后所规定的,从而使得正常使用极限状态下基于挠度的荷载效应也只能考虑汽车荷载,从而使得汽车荷载效应对可靠度指标的影响程度增大,进而导致各梁可靠度指标差别较大。
总体看来,采用CFRP板加固虽然在承载能力方面有其固有的优势,但在正常使用要求方面还存在不足。对于今后采用CFRP板加固还需考虑加强其刚度的措施使之既能满足承载能力要求又能满足正常使用能力要求。
5 结 论
用模糊当量法将正常使用极限状态的抗力当量作为在一定区间内的均匀分布函数,建立了服役桥梁在加固完成时正常使用极限状态荷载效应的均值和标准差模型,并发展了基于挠度的正常使用极限状态方程。通过计算分析,可以得出如下结论:
1)以一座现役T型梁桥为例,计算了其采用CFRP板加固完成时和加固后的可靠度,用CFRP板加固后,1号梁仍不能满足要求,3片梁可靠度指标平均提高0.255 9,说明目前采取碳纤维板加固桥梁在正常使用能力可靠性上面的欠缺。
2)对桥梁加固后各梁可靠度指标进行计算表明,在加固后50年服役中,只有3号梁一直能满足目标可靠度区间要求,更进一步说明,CFRP板加固桥梁在基于挠度可靠性方面的不足。
[1] 刘伟强.钢筋混凝土桥梁构件正常使用极限状态可靠度分析[J].
现代测量与实验室管理,2005(2):16-18. LIU Weiqiang. Reliability analysis for normal limited state of RC bridges member[J].AdvancedMeasurementandLaboratoryManagement,2005(2):16-18.
[2] 赵羽习,金伟良.混凝土构件正常使用极限状态的可靠度计算[J].工业建筑,2002,32(5):60-64. ZHAO Yuxi, JIN Weiliang. Reliability analysis for normal limited state of reinforcement concrete member[J].IndustrialConstruction,2002,32(5):60-64.
[3] 唐铁羽,赵国藩.钢筋混凝土构件耐久性可靠度分析[C]∥中国土木工程学会桥梁及结构工程学会结构可靠度委员会.工程结构可靠性第三届学术会议论文集.南京:河海大学,1992. TANG Tieyu, ZHAO Guofan. Reliability analysis for durability of RC members[C]∥China Civil Engineering Academy Bridge and Structure Committee Structure Reliability Commission.TheThirdAcademicConferenceProceedingsforEngineeringStructureReliability.Nanjing:Hohai University,1992.
[4] 中交公路规划设计院.公路钢筋混凝土及预应力混凝土桥涵设计规范:JTGD62—2012[S]. 北京:人民交通出版社,2012. CCCC Highway Consultants Co.,Ltd.CodeforHighwayConsultantsReinforcedConcreteandPrestressedConcreteBridgesandCulverts:JTGD62—2012[S]. Beijing: China Communications Press,2012.
[5] 中国建筑科学研究院.混凝土结构设计规范:GB50010—2010 [S]. 北京:中国建筑工业出版社,2010. China Academy of Bridge Research.CodeforDesignofConcreteStructures:GB50010—2010[S]. Beijing: China Architecture & Building Press,2012.
[6] 张皓,曹双寅.预应力碳纤维布加固钢筋混凝土梁刚度计算分析[J]. 工程抗震与加固改造,2009,31(6):19-23. ZHANG Hao,CAO Shuangyin.Calculational analysis of stiffness of strengthened RC beam prestressed with CFRP sheet[J].EarthquakeResistantEngineeringandRetrofitting,2009,31(6):19-23
[7] 李扬海,鲍卫刚,郭修武,等.公路桥梁结构可靠度与概率极限状态设计[M].北京:人民交通出版社,1997:141-142. LI Yanghai, BAO Weigang, GUO Xiuwu,et al.ReliabilityofHighwayBridgeStructureandtheProbabilityLimitStateDesign[M]. Beijing: China Communications Press,1997:141-142.
[8] 张建仁,毛杰,彭建新,等. 使用碳纤维板加固的RC梁桥服役过程的可靠度指标分析[J].长沙理工大学学报,2014,11(2):25-31. ZHANG Jianren, MAO Jie, PENG Jianxin,et al. Analysis for the reliability index of RC beam bridges strengthened with carbon fiber plate in service process [J].JournalofChangshaUniversityofScienceandTechnology,2014,11(2):25-31.
Dynamic Reliability Analysis of Serviceability State for RC Beam Bridges Strengthened with CFRP Sheet
CHEN Qiang
(Shool of Civil Engineering,Hunan City University, Yiyang 413000,Hunan,P.R.China)
The model simulating the mean and standard deviation of load effects for serviceability limit state of RC beam bridge strengthened by CFRP sheets were developed, and then the fuzzy equivalent method was used to convert deflection equivalent under serviceability limit state of bridge in service into equivalent uniform-distribution function in a certain range. On basis of this, the formulation for serviceability limit state of RC beam bridge strengthened with CFRP sheets was formulated. Combined with an actual bridge strengthened with CFRP, the JC checking point method was employed to calculate the dynamic reliability index of serviceability limit state at the completion of reinforcing works and in some time after such strengthening work done. The study findings show that after the bridge being reinforced with CFRP, #1 girder still fails to satisfy the required normal serviceability and #2 girder, and after being reinforced and serving over 30 years still fails to satisfy the required normal serviceability, both of which indicate the defect of the currently applied CFRP in respect of reliability of normal serviceability of bridge strengthened with CFRP.
bridge engineering;RC beam bridge; CFRP sheet strengthening; fuzzy equivalent method; JC checking point method; dynamic reliability index
10.3969/j.issn.1674-0696.2016.05.02
2015-09-09;
2015-10-23
湖南省科技厅科技计划项目(2012GK3066)
陈 强(1968—),男,湖南常德人,副教授,硕士,主要从事桥梁结构理论分析方面的研究。E-mail:846039016@qq.com。
U447
A
1674-0696(2016)05-005-04

