冻胀力作用下土质隧道衬砌内力影响因素敏感度分析
黄 杰,师亚龙,刘志强
(1.四川交通职业技术学院,四川 成都 611130;2.中铁西南科学研究院有限公司,四川 成都 611731)
冻胀力作用下土质隧道衬砌内力影响因素敏感度分析
黄 杰1,师亚龙2,刘志强2
(1.四川交通职业技术学院,四川 成都 611130;2.中铁西南科学研究院有限公司,四川 成都 611731)
运用有限元数值模拟,计算分析了隧道衬砌内力(弯矩、轴力、最大拉应力)对土体冻胀率、冻结圈厚度、衬砌厚度、围岩弹模的敏感度。研究表明:隧道衬砌弯矩、轴力及拉应力对围岩自由冻胀率均敏感;隧道衬砌轴力、拉应力对围岩弹模敏感,而隧道衬砌弯矩对围岩弹模的敏感度较小;隧道衬砌内力受冻结圈深度影响较为明显,而衬砌厚度对衬砌内力影响相对最弱。建议对于季节性冻土区隧道设置保温隔热层及在衬砌背后一定范围内的注浆。
隧道工程;冻胀力;土质隧道;影响因素;敏感度
我国西部地区地形、地质构造条件复杂,随着我国交通网的不断完善,一批跨越季节性冻土区域与多年冻土区域的隧道不断涌现。然而在这些区域修建构筑物,首先应解决的是结构物冻胀问题,对于隧道结构则应避免围岩冻胀或融沉,使隧道衬砌结构开裂,影响其寿命[1-2]。
笔者主要讨论冻胀力作用对隧道衬砌结构内力的影响。影响隧道冻胀力的主要因素有:围岩自由冻胀率、冻结圈深度、衬砌厚度及围岩弹模。为此笔者借助于敏感度分析讨论这4种因素对隧道衬砌内力的影响。敏感性分析作为系统分析中研究系统稳定性的重要方法,其引入到岩土工程领域并得到了广泛应用。
目前在隧道领域,运用敏感度分析的文献主要有:王辉等[3]以嘎隆拉隧道为研究背景,通过敏感性分析方法,研究围岩力学参数对变形的敏感;研究表明,拱顶沉降对弹性模量比较敏感,对其它参数的敏感性相对较小;而周边收敛则相反,泊松比、内摩擦角、黏聚力要比弹性模量更为敏感。徐颖等[4]通过现场试验与数值计算相结合的方法,对软岩的各力学参数对隧道力学特征响应的敏感性分析;结果表明隧道洞周位移受E影响最大,其次为μ,且二者敏感度远大于c,φ的敏感度。张志华等[5]和王迎超等[6]分别通过研究土体力学参数的变化对地铁隧道开挖围岩稳定性进行敏感度分析。由上述学者的研究可以看出,目前在隧道领域运用敏感度分析,更多的是对围岩力学参数的敏感度分析来判别隧道开挖后的围岩稳定性。而对于外因作用下(如冻胀力)隧道衬砌结构的稳定性分析较少。笔者针对冻胀力影响因素对衬砌结构内力影响进行敏感度分析,寻求影响衬砌结构内力的最敏感因素,以便避免或减弱该因素对衬砌结构的影响,进而指导冻土区域隧道工程的修建。由于岩石隧道的冻胀与土质隧道冻胀产生机理有较大区别,笔者只对土质隧道进行研究分析。
1 敏感度分析方法

参考章光等[7]对敏感度定义:
(1)

Sk值越大,则在基准状态下,衬砌内力Q对参数xk越敏感。通过对Sk的比较,则可以评价衬砌内力系统特性对各因素的敏感性程度。每次只变动其中1个因素,而保持其他因素不变。根据我国西部某在建铁路工程沿线地质勘察报告参数变化范围[8],每个因素选取的基准值及变化范围见表1,分别对自由冻胀率(e)、冻结圈深度(d)、衬砌厚度(h)以及围岩弹模E对冻胀力的影响进行分析。得到每一组参数影响下的衬砌内力值,按照式(1)定义的敏感度,计算各参数的敏感度。

表1 各参数基准值及变化范围
2 基于有限元法的敏感度计算分析
2.1 计算模型
笔者采用4节点四边形单元,通过温度改变来为冻结圈内围岩提供冻结时的体积膨胀,同时改变冻结围岩的物理、力学参数,本着“位移响应、刚度分配”的法则,建立围岩冻胀力计算模型。此时围岩与衬砌分别采用plane42平面实体单元与beam3梁单元进行模拟。计算采用弹塑性模型,围岩采用Drucker-Prager屈服准则,隧道衬砌结构采用弹性材料。其计算范围取为左右边界及下边界分别距隧道中心30 m,埋深取为15 m,其有限元计算模型如图1。力学边界条件均采用位移边界条件,顶面取自地面,为自由面,两侧面、底面施加法向约束。

图1 隧道有限元网格模型Fig.1 The tunnel finite element mesh model
2.2 计算工况及基本参数
影响隧道冻胀力大小的主要因素为:围岩线冻胀率、冻结圈厚度、衬砌厚度、围岩弹模等。首先利用ANSYS中的温度场模块根据材料的热胀冷缩特性,设置冻结圈围岩的温度与其他部分围岩参考温度之间存在一定的温度差,进而实现冻结圈围岩的冻胀特性,然后将温度场转换到应力场进行温度场与应力场耦合分析。笔者通过计算围岩线冻胀率分别为0.54%,1.08%,1.62%,2.16%,2.70%,衬砌厚度分别为40,50,60,70,80 cm,冻结圈厚度分别为30,40,50,60,70 cm,围岩弹性模量分别为80,160, 320, 640,1 280 MPa工况的隧道衬砌内力。对该4种因素进行分析,寻求影响冻胀力大小的最敏感的因素,并对该4种因素进行敏感度排名,以便今后对冻土区隧道设计提供理论参考。计算参数见表2。

表2 围岩及衬砌物理力学参数
2.3 隧道衬砌内力计算结果
将其它参数保持不变,分别对隧道围岩自由冻胀率e,冻结圈深度d,衬砌厚度h和围岩弹性模量E对隧道衬砌内力的影响进行分析,见图2~图4。由图2~图4可知,该4种因素与隧道衬砌内力几乎全部呈现出线性关系(除围岩弹模与隧道衬砌弯矩呈现出多项式关系)。隧道衬砌弯矩、轴力的绝对值均随e,d,h,E的增大而增大。而在隧道衬砌拉应力关系中,围岩自由冻胀率与冻结圈深度对隧道衬砌拉应力呈现正相关性,隧道衬砌拉应力分别随两者数据的增大而增大。而隧道衬砌厚度与围岩弹模对隧道衬砌拉应力则呈现出负相关性,隧道衬砌拉应力随两者数据的增大反而减小。

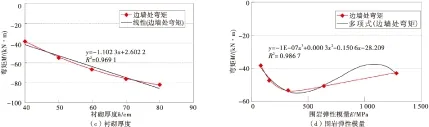
图2 各参数与隧道衬砌内力(弯矩)的变化关系Fig.2 Relationship between parameters and internal force of tunnel lining(bending moment)


图3 各参数与隧道衬砌内力(轴力)的变化关系Fig.3 Relationship between parameters and internal force of tunnel lining(axial force)


图4 各参数与隧道衬砌内力(拉应力)的变化关系Fig.4 Relationship between parameters and internal force of tunnel lining(tensile stress)
2.4 敏感度计算结果
由式(1)计算得隧道衬砌内力对围岩各参数的敏感度数值见表3。

表3 衬砌内力对各参数的敏感度
从表3可以看出,隧道衬砌内力对影响冻胀力的4个参数的敏感度是不一样的。隧道衬砌弯矩对各参数的敏感度排序为自由冻胀率、冻结圈深度、衬砌厚度、围岩弹性模量。而对于衬砌轴力对各参数的敏感度排序为:围岩弹性模量、围岩自由冻胀率、冻结圈深度、衬砌厚度。由表3可知,衬砌弯矩对围岩弹模的影响最不敏感。而其对于衬砌轴力则最为敏感。由于衬砌轴力均为负即受压,在进行拉应力计算时,围岩弹模的提高可以大幅度地降低隧道衬砌抗裂能力。对于拉应力敏感度排序为:围岩自由冻胀率、围岩弹性模量、冻结圈厚度、衬砌厚度。因此,对于冻胀力作用下的隧道衬砌内力最不利因素为围岩自由冻胀率,降低围岩自由冻胀率是减轻隧道衬砌病害最有效的方法。
在隧道施工中,对围岩进行背后注浆,减小围岩的孔隙率进而减小围岩自由冻胀率,同时围岩弹性模量亦有相应程度的提高。而隧道衬砌内力对冻结圈深度也是较为敏感,对于特别寒冷的地区可以在衬砌中设置保温隔热层来降低围岩冻结圈深度。总体来说,隧道衬砌内力对隧道衬砌厚度的敏感度最弱,因此对于在冻土区域修建隧道,靠增加衬砌厚度来提高其结构的抗冻、抗裂能力是不可行的。
3 结 论
1)冻胀力作用下隧道衬砌拉应力与围岩自由冻胀率、冻结圈深度呈正相关性,隧道衬砌内力受围岩自由冻胀率敏感性最强。而隧道衬砌拉应力与围岩弹模、衬砌厚度呈现负相关性,隧道衬砌拉应力对衬砌厚度的敏感性最弱。
2)自由冻胀率、围岩强度、冻结圈深度、衬砌厚度对隧道衬砌内力影响大部分呈现出线性关系,因此其敏感度可以通过其斜率的变化来分析其敏感性的强弱。综上可知,其敏感度由强到弱分别为:自由冻胀率、围岩强度、冻结圈深度、衬砌厚度。
3)通过对冻胀力作用下隧道衬砌内力敏感度分析可知,对于冻土区域修建的隧道,通过提高二次衬砌厚度来增加衬砌结构抗裂性是行不通的。
4)对于季节性冻土区修建隧道,为防其衬砌冻胀开裂,关键是减小围岩的自由冻胀率,其次提高围岩的弹性模量,最后减小冻结圈厚度。主要应采取的工程措施为:① 衬砌背后最大限度的进行注浆,注浆管布置要密且打入深度要大;② 对于冻结深度较大地区,还要在隧道不同位置设置保温隔热层,从而减小围岩冻结圈深度。
[1] 夏才初,黄继辉,韩常领,等. 寒区隧道岩体冻胀率的取值方法和冻胀敏感性分级[J]. 岩石力学与工程学报,2013,32(9):1876-1885. XIA Caichu, HUANG Jihui, HAN Changling, et al. Methods of frost-heave ratio evaluation and classification of frost-heave susceptibility of tunnel surrounding rocks in cold regions[J].ChineseJournalofRockMechanicsandEngineering, 2013,32(9):1876-1885.
[2] 冷毅飞,张喜发,张冬青. 季节冻土区公路路基细粒土冻胀敏感性研究[J]. 冰川冻土,2006,28(2):211-216. LENG Yifei, ZHANG Xifa ,ZHANG Dongqing. Study of frost heaving susceptibility of fine-grain soil of highway subgrade in seasonally frozen ground regions[J].JournalofGlaciologyandGeocryology,2006,28(2):211-216.
[3] 王辉,陈卫忠. 嘎隆拉隧道围岩力学参数对变形的敏感性分析[J].岩土工程学报,2012,34(8):1548-1553. WANG Hui, CHEN Weizhong. Sensitivity analysis of mechanical parameters to deformation of surrounding rock in Galongla tunnel[J].ChineseJournalofGeotechnicalEngineering,2012,34(8):1548-1553.
[4] 徐颖,陈建平,左昌群,等. 软岩力学参数对隧道力学特征响应的敏感性分析[J].中外公路,2013,33(1):195-198. XU Ying, CHEN Jianping, ZUO Changqun, et al. Sensitivity analysis of soft rock mechanical parameters to tunnel mechanical characteristics response[J].JournalofChina&ForeignHighway,2013,33(1):195-198.
[5] 张志华,周传波,夏志强,等. 地铁隧道土体参数敏感性分析与正交反演[J]. 中南大学学报(自然科学版),2013,44(6):2488-2493. ZHANG Zhihua, ZHOU Chuanbo, XIA Zhiqiang, et al. Sensitivity analysis and orthogonal backward analysis of soil parameters for subway tunnel[J].JournalofCentralSouthUniversity(ScienceandTechnology),2013,44(6):2488-2493.
[6] 王迎超, 尚岳全, 徐兴华. 浅埋隧道岩土体参数正交反演及衬砌工作状态评价[J]. 中南大学学报(自然科学版),2011,42(6):1764-1771. WANG Yingchao, SHANG Yuequan, XU Xinghua.Orthogonal back-analysis of geotechnical parameters and working state evaluation of lining of shallow buried tunnel[J].JournalofCentralSouthUniversity(ScienceandTechnology),2011,42(6):1764-1771.
[7] 章光,朱维申. 参数敏感性分析与试验方案优化[J].岩土力学,1993,14(1):51-58. ZHANG Guang, ZHU Weishen. Parameter sensitivity analysis and optimizing for test programs[J].RockandSoilMechanics,1993,14(1):51-58.
[8] 铁道部第三勘查设计院集团有限公司.朔州至准格尔铁路工程地质勘查报告[R].天津: 铁道部第三勘查设计院集团有限公司,2008:68-264. The Third Railway Survey and Design Institute Group Corporation.TheGeologicalSurveyReportofShuozhoutoZhungeerRailwayEngineering[R].Tianjing: The Third Railway Survey and Design Institute Group Corporation,2008:68-264.
Sensitivity Analysis of Influences on Internal Force of Soil Tunnel Lining under Frost Heave Force
HUANG Jie1,SHI Yalong2,LIU Zhiqiang2
(1. Sichuan Vocational and Technical College of Communications, Chengdu 611130, Sichuan,P.R.China; 2.CREC,Southwest Research Institute Co.,Ltd., Chengdu 611731, Sichuan,P.R.China)
The influences of tunnel lining internal forces (bending moment, axial force and maximum tensile stress) on soil frost heave ratio, frozen ring thickness, lining thickness and rock elastic modulus were simulated, calculated and analyzed by use of finite element numerical model and then the relations between them were also analyzed. The results indicate that the free frost heaving ratios of surrounding rock affected tunnel lining moment, axial force and tensile stress significantly while tunnel lining moment had small influence on ground elastic modulus and tunnel lining internal forces were notably influenced by depth of frozen ring while lining thickness had relatively weak influence on lining internal forces. It is thus suggested that thermal insulation be provided in seasonably frost soil zone and grouting injected in certain area behind the lining.
tunnel engineering;frost heaving force;soil tunnel;influence factors:sensitivity
10.3969/j.issn.1674-0696.2016.05.05
2015-10-13;
2015-11-10
中国中铁股份有限公司科技开发计划课题[(2013)-Y195-KJ014-SD]
黄 杰(1981—),男,四川泸州人,工程师,硕士,主要从事桥梁与隧道工程方面的研究。E-mail:hj8100@163.com。
U451+4
A
1674-0696(2016)05-017-05

