再谈“对一道高考试题的质疑与探究”
浙江省温州中学 (325014) 吴时月
再谈“对一道高考试题的质疑与探究”
浙江省温州中学(325014)吴时月
抽象函数的对称性、周期性是高中数学的重点内容之一,这类问题由于抽象程度高,解答过程灵活,不仅学生难以把握,老师在命题时也会经常出错.近期,笔者在查阅文献时,看到文【1】中的“对一道高考试题的质疑与探究”,深有感触,并对此类问题进行更深入的思考,作为对文【1】探究的继续,现记述如下.
一、真题再现
(2005福建理)已知f(x)是定义在R上的以3为周期的奇函数,且f(2)=0,则方程f(x)=0在区间(0,6)内解的个数的最小值是().
A.2B.3C.4D.5
命题组提供的流行错解:f(2)=f(5)=0,f(0)=f(3)=0,f(2)=f(-1)=-f(1)=-f(4)=0,所以f(1)=f(4)=0.所以答案选D.
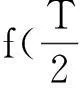
(2005福建文)已知f(x)是定义在R上的以3为周期的偶函数,且f(2)=0,则方程f(x)=0在区间(0,6)内解的个数的最小值是().
A.5B.4C.3D.2
命题组提供的基本解法:f(2)=f(5)=0,f(2)=f(-2)=f(1)=f(4)=0,此解法则是正确无疑,相比于理科题,条件仅由奇函数变成偶函数,结果则是大相径庭.
二、错题剖析
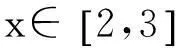
此题是在讲授抽象函数的内容时经常遇到的一道错题,下面先提供学生的两种解法:

解法一、二的图像延拓如图1:
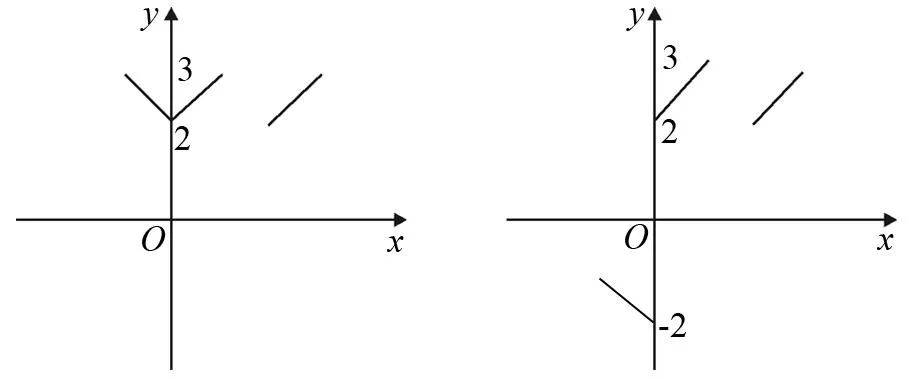
图1
两种解法的答案为什么不一致呢?很多学生都找不出错误的地方.究其原因,是因为f(x)是偶函数的条件多余,从而导致自相矛盾的表达式;或者把条件f(x+1)+f(x)=1改为f(x+2)=f(x),则函数的表达式就唯一确定了,深究原因,是因为条件f(x+1)+f(x)=1在给出周期性的同时,还可以利用此条件得到相应区间的表达式,造成自相矛盾的结果. (或者说:f(x+1)+f(x)=1只是f(x+2)=f(x)的充分不必要条件,而不是充要条件)
以下的例题也是很多复习参考书中经常出现的错题:


A.是增函数,且f(x)<0
B.是增函数,且f(x)>0
C.是减函数,且f(x)<0
D.是减函数,且f(x)>0
只要稍加修改,以上错题便可成为典型的例题:



A.是增函数,且f(x)<0
B.是增函数,且f(x)>0
C.是减函数,且f(x)<0
D.是减函数,且f(x)>0

A.是增函数,且f(x)<0
B.是增函数,且f(x)>0
C.是减函数,且f(x)<0
D.是减函数,且f(x)>0
以典型例题3″为例,下面提供两种常用的解法:

解法一、二的图像延拓如图2:

图2
三、典例探究
典型例题5定义在R上的奇函数f(x)满足f(3+x)=f(3-x),若当x∈(0,3)时,f(x)=2x,则当x∈(-6,-3)时,f(x)=() .
A. 2x+6B. -2x+6C.2x-6D.-2x-6
典型解法一:由f(x+6)=f(-x),f(-x)=-f(x)得f(x+6)=-f(x).当x∈(-6,-3)时,x+6∈(0,3),所以f(x+6)=2x+6=-f(x),即f(x)=-2x+6.选B.
典型解法二:当x∈(3,6)时,6-x∈(0,3),所以f(x)=f(6-x)=26-x,当x∈(-6,-3)时,-x∈(3,6),所以f(x)=-f(-x)=-2x+6.
解法一、二的图像延拓如图3所示:

典型例题5′定义在R上的奇函数f(x)满足f(3+x)=f(3-x),若当x∈(0,3)时,f(x)=2x,当x∈(-12,-9)时,求f(x)的表达式.
解:当x∈(-12,-9)时,x+12∈(0,3),所以f(x+12)=212+x=-f(x+6)=f(x),即当x∈(-12,-9)时,f(x)=212+x.
此题背后隐藏着抽象函数的另一个重要性质(如图4):既有对称中心,又有对称轴的函数,必有周期. 具体性质如下:
性质1若函数y=f(x)关于点(a,y0)和直线x=b对称,则4|b-a|是函数y=f(x)的一个周期.
性质2若函数y=f(x)关于直线x=a和x=b对称,则2|b-a|是函数y=f(x)的一个周期.
性质3若函数y=f(x)关于点(a,y0)和点(b,y0)对称,则2|b-a|是函数y=f(x)的一个周期.
四、反思总结
每一个数学问题都有它的数学本质,面对一个问题,如果只看到问题的表层,就无法深入到问题的内核,看不透问题的本质,正所谓“不识庐山真面目,只缘身在此山中” .所以,在平时的解题和探究过程中就应该通过问题的解决揭示问题的本质,使数学问题的解决变得简单而自然.
参考文献
[1] 马进才.对一道高考试题的质疑与探究[J].数学通讯,2013(9).

