一道无理函数题的解法与变式探究

江西省信丰中学　(341600)　何春良



一道无理函数题的解法与变式探究

江西省信丰中学(341600)何春良

这道题主要考查了无理函数值域的求法.在高中数学中，函数值域的求法主要有：观察法、反函数法、分离常数法、配方法、换元法、判别式法、等式法、单调性法、求导法、函数的有界性法、数形结合法等等.下面笔者先来探究这道无理函数题值域的解法：

解法2：(反函数法)由于y=x+

对于这两种求函数值域的解题思想方法，笔者在平时的解题教学中多次渗透，学生也知道求函数值域的一些基本方法，但运用起来就是达不到应用自如与触类旁通的效果．这道题对笔者引发了一些思考，联想到这一类型的无理函数题值域的求解方法.下面笔者就对这道无理函数题进行变式探究：

点评：这道题虽含根式看似很复杂，但若分析其单调性来求值域就很简单了.因此对某些求函数的值域或最值问题，可以从函数的单调性角度来考虑.

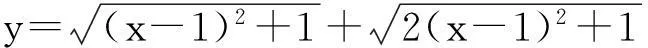
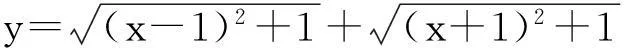
点评：此题若从函数的单调性角度来考虑，很容易得到当x∈(-∞,-1]时，函数单调递减；当x∈[1,+∞)时，函数单调递增，但是当x∈(-1,1)时不好判断.若此题从几何意义的角度来考虑就很简单了.

我们知道数学题的解法有时候不是唯一的，方法选择不当时会导致求解过程也较繁杂甚至有时候算不到答案.这就需要我们平时解完了一道题后，要及时归纳与总结方法，力求能解决这一类问题，并做到一题多解、多题一解与一题多变，达到应用自如与触类旁通的境界，为以后提高解题效率打好坚实的基础.