2015年全国初中数学联赛第5题的多方位探究*

江苏苏州市田家炳实验高级中学　(215004)　王　耀



2015年全国初中数学联赛第5题的多方位探究*

江苏苏州市田家炳实验高级中学(215004)王耀

在2015年全国初中数学联赛试卷中，有一道含二元变量的最值问题，设计精巧，内涵丰富，并且这种问题也常出现在高中各类数学考试中，笔者将以此题为例，从不同的审题角度出发去探究其解法，整理成文与读者交流.

1.问题再现

已知实数x，y满足关系式xy-x-y=1，则x2+y2的最小值为 ().

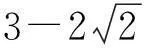
2.分析视角与解法探究

(1) 分析视角1——函数与方程思想

由题设关系式得到x+y和xy的相互联系，由此可结合韦达定理根据两根关系构造一元二次方程，进而再由方程有解去挖掘隐含条件，具体解法如下：

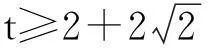
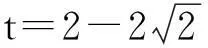
(2) 分析视角2——基本不等式法

许多求最值的问题除了转化为函数最值问题外，也可利用基本不等式法去求解，能得到如下两种解法：

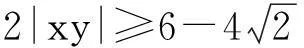
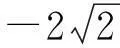
评注1:解法2利用了基本不等式和二元不等式4xy≤(x+y)2，顺利解题，这里的重要不等式本质上与解法1中判别式Δ≥0是一致的；解法3则利用了消元法和换元法，局部构造基本不等式结构解题，这种先减元再换元的分析方式是解决问题的常规思路.

(3)分析视角3——数形转化思想

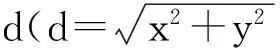
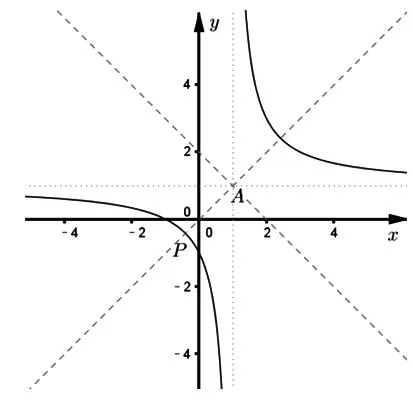
图1

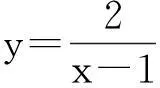
图2

其次，解法5利用导数和切线方程联立方程组解出切点和斜率，利用双曲线的对称性也能立即得到切线与直线y=x垂直，即斜率为-1.

(4)分析视角4——三角换元法

在分析x2+y2的范围问题时，也常采用三角换元法进行求解，进而将不等式问题可转化为函数与方程问题，即化为等式问题进行分析.

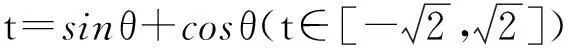
(5)分析视角5——和差换元法

在含有二次项xy的等式中，可利用和差换元法将所有的二次项全部转化为平方项，从而可将问题简单化，体现其本质.

评注3:本解法的几何本质即为通过旋转变换,将双曲线转化为关于x轴对称的等轴双曲线.亦可采用类似解法3中的数形结合法迅速解题，此处不再赘述.

(6)分析视角6——引参代换法

由于xy-x-y-1=0，故可以考虑进行引参并整体代换后得到曲线系方程，从而可进行配方法解题.

评注4:本解法采用这种待定系数法的灵感来自于高等数学中的拉格朗日乘法求极值，高等数学中采用求偏导的方法，而上述配方法也能充分体现初等数学的乐趣和魅力.

3结语

“让学生体会到思维过程”——一直是笔者在数学解题教学中遵循的基本原则. 因此，在前文中，笔者尝试从不同的审视角度对一道联赛题进行一题多思，从多角度、多方位地去探讨问题的实质，并体会数学思想和解题的方法，文中给出的方法既有常规的通法，也有一些转化技巧的分析；研究这些不同的分析转化思维，能更好地梳理和构建知识框架，更为重要的是能从这些不同的思维发展过程中，培养思维的创造性，树立全方位、多角度审视问题的观念，从而培养良好的数学思维品质.

*本文是江苏省教育科学“十二五”规划2015年度立项课题《高中数学研究性学习的实践与认识》(编号：B-b/2015/02/119)的研究成果之一.