一道数学高考题的多解和推广

山东省聊城大学数学科学学院(252000)　夏迎雪　于兴江



一道数学高考题的多解和推广

山东省聊城大学数学科学学院(252000)夏迎雪*于兴江

2015年浙江高考理科卷第19题为解析几何题，主要考察直线与圆锥曲线综合，并结合面积最大值问题进行综合考察.在解题过程中，考生要熟练掌握直线与圆锥曲线的基本计算方法.对韦达定理的使用、交点存在性的判断、不等式解法等知识点的要求较高.笔者给出此题的多种解法，并利用几何画板对三角形面积最大值问题进行探究，从而推广出一般性的结论.

图1

(1)求实数m的取值范围；

(2)求ΔAOB面积的最大值.

1.第(1)问的两种解法

2．第(2)问的三种解法

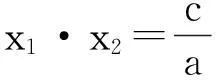
解法2：由正弦定理变形可得

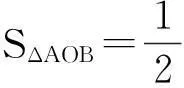
解法3:不妨设AB所在直线与x轴交于点N，第一问中已经求出交点N的横坐标xN=b=

3．探究推广

在历年高考数学中，圆锥曲线问题是必考题型，求两个交点和原点O所构成的三角形的面积问题更是高考中的热点题型.笔者现给出如下结论：

下面分情况讨论：

图① 图② 图③

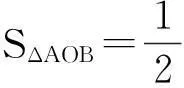
情况1若0<|m|

图④ 图⑤ 图⑥

参考文献

[1]柳俊婷，于兴江.关于最大值的两个定理[J].聊城大学学报(理科版)，2015,2.

[2]孙玉英，于兴江.探究引申剖析启示——一道高考题的赏析[J].中学数学研究(江西)，2013,10.