抑制风力机疲劳载荷的直接比例谐振独立变桨控制策略

李 辉 ，杨 超 ，2，胡姚刚 ，李 洋 ，梁媛媛 ，欧阳海黎

（1.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044；2.国网冀北电力有限公司秦皇岛供电公司，河北 秦皇岛 066004；3.重庆科凯前卫风电设备有限责任公司，重庆 401121；4.中船重工（重庆）海装风电设备有限公司，重庆 401122）

0 引言

随着风电机组单机容量的持续增长，风力机尺寸不断增大，机组变得柔性大、阻尼小，承受的动态载荷显著增加，这对机组长期安全运行带来巨大风险［1-3］。研究风电机组的载荷主动控制技术，对未来大型机组寿命的提高及发电成本的降低具有重要意义。

独立变桨控制策略能够大幅降低作为机组载荷源头的叶片载荷，同时又不会引起其他部件载荷的增加，因此受到了越来越多的关注。受重力、风切等因素影响，风力机系统具有周期时变的特点，针对该问题，文献［4-5］提出了基于科尔曼坐标变换的独立变桨控制策略，该策略通过科尔曼变换方法将叶根弯矩一倍叶轮转频（1p）周期载荷转化为静态轮毂倾覆和偏航力矩载荷，然后利用比例积分（PI）控制器减小该静态载荷及叶片1p周期载荷。但是该控制策略忽略了风力机的高次谐波载荷，而其也是引起风力机结构损伤的主要因素。为减小高次谐波载荷，文献［6-7］进一步研究了基于改进科尔曼坐标变换的独立变桨控制策略。从控制的角度来看，科尔曼坐标变换虽然能够将周期时变的风力机系统变换为时不变系统，但是给倾覆和偏航变量带来了较为严重的耦合［8］，因此，利用经典单输入单输出（SISO）理论设计的控制器参数难以保证系统的控制性能。后续研究相续提出了一些基于多变量控制理论的独立变桨控制策略，例如，反馈前馈［9］、线性二次型调节器（LQR）［10］、线性二次高斯（LQG）［11］、H∞［8，12］等独立变桨控制策略。虽然这些多变量控制方法提高了科尔曼坐标变换后耦合系统的控制性能，但上述控制策略仍以坐标变换为基础，系统结构较为复杂；另外，上述控制策略在设计控制器参数时，不仅要将风力机和变桨驱动系统的模型进行科尔曼坐标变换，且需考虑科尔曼变换本身的动态特性［12］，导致控制器参数设计的难度也大幅增加。文献［13］借鉴电机系统的谐波控制方法，在Clark坐标变换的基础上，提出了利用比例谐振（PR）控制器抑制谐波载荷的独立变桨控制策略，该控制策略虽结构相对简单，但Clark坐标变换显著增加了系统的参数时变特性，而文献并未对控制策略在系统参数时变下的性能进行详细分析；另外，随着叶片长度和柔性的不断增加，叶片的动态特性变得不可忽略，加之变桨驱动系统引起的延迟，将导致桨距角参考给定值和叶片输出载荷之间产生较大的相位偏移，考虑到该问题，文献所提独立变桨控制策略的载荷抑制效果可能会大打折扣。因此，从减小传统独立变桨控制策略参数耦合影响出发，并考虑风力机的周期时变特性，进一步研究有效的独立变桨控制策略，并分析其性能十分必要。

基于此，为更有效地减小风力机的谐波载荷，本文提出了一种新颖的无需坐标变换的直接PR独立变桨控制策略，并试图从频域角度分析控制策略在参数时变情况下的稳定性。该控制策略以单个叶片的叶根弯矩为被控变量，从而避免了传统独立变桨控制策略中坐标变换给控制系统带来的结构复杂、参数耦合及随之而来的控制器参数设计困难等问题；同时，PR控制器在谐振点的增益非常高、在其他频率处的增益迅速衰减的特点，也使控制系统对风力机参数周期时变具有一定的鲁棒性。文章首先分析叶片根部弯矩载荷对轮毂载荷的影响规律及其抑制机理；然后，给出所提直接PR独立变桨控制策略，详细阐述基于周期时变叶片系统的平均线性化模型设计相位补偿器和控制器参数的方法，并对所提控制策略的稳定性进行频域分析；最后，通过建立风电机组载荷及控制联合模型进一步仿真验证所提独立变桨控制策略的有效性。

1 考虑谐波影响的风力机结构载荷分析

风速的塔影效应和风切效应导致风力机叶根拍打弯矩产生周期性变化，其是风力机周期载荷的源头。叶根拍打弯矩变化周期与叶片在风轮扫略面内所处位置角有关，可表示为 Mi（φi）（i=1，2，3）的形式，其中φi表示第i个叶片在叶轮扫略面内的方位角。假设 φ1=φ=ωrt，其中 ωr为叶轮转速，则 φ2=φ+2π/3，φ3=φ+4π/3。

周期性叶根拍打弯矩可分解为直流分量、基频分量和高次谐波分量，如下式所示：

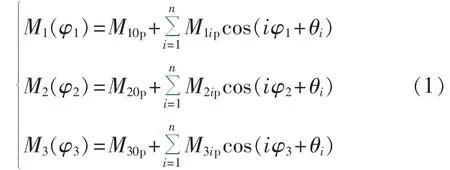
其中，M10p、M20p、M30p分别为叶片 1、2、3 的叶根拍打弯矩直流分量；M1ip、M2ip、M3ip分别为叶片 1、2、3 叶根拍打弯矩 i（i=1，2，…，n）倍叶轮转频（ip）分量的幅值；θi为叶根拍打弯矩ip分量的初始相角。对于叶轮平衡的风力机，各叶片叶根拍打弯矩的各次谐波分量的幅值分别相等，假设M10p=M20p=M30p=M0p，M1ip=M2ip=M3ip=Mip。

对于上风向风力机，忽略传动轴的仰角影响，根据叶片旋转坐标系和轮毂固定坐标系之间关系，可得叶根拍打弯矩与轮毂倾覆和偏航力矩的关系为［14］：

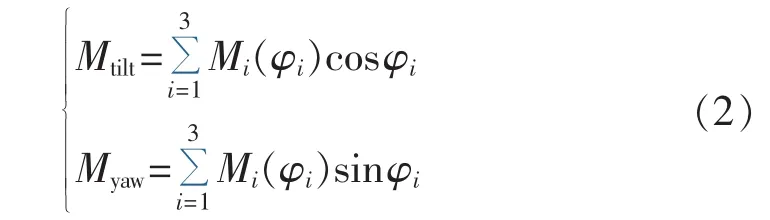
其中，Mtilt和Myaw分别为轮毂倾覆和偏航力矩。

叶根拍打弯矩以 0p、1p、2p、3p和 4p载荷分量为主。将式（1）的叶根拍打弯矩的主要谐波载荷分量分别代入式（2），可得出各次谐波载荷分量对倾覆和偏航力矩的影响。

a.叶根拍打弯矩0p载荷分量的影响：

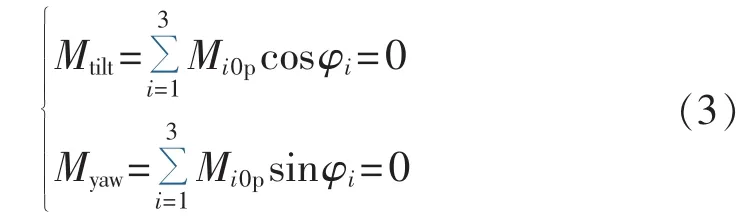
b.叶根拍打弯矩的1p载荷分量的影响：

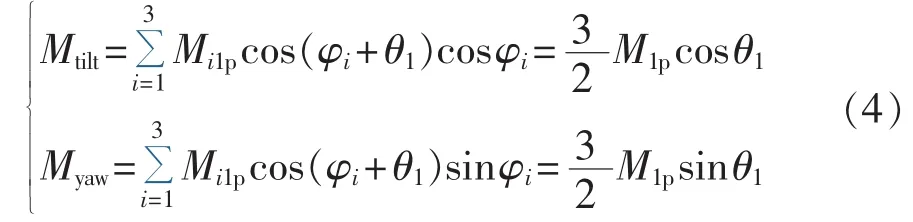
c.叶根拍打弯矩2p载荷分量的影响：

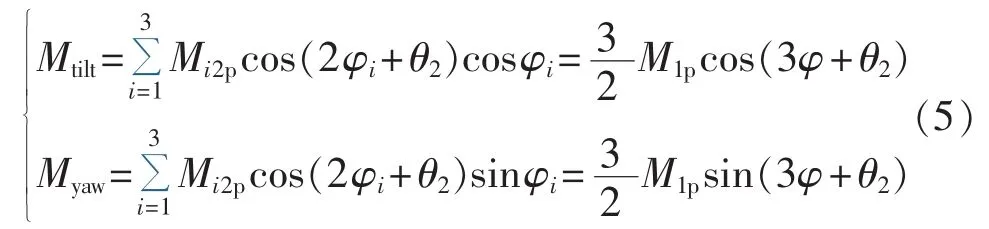
d.叶根拍打弯矩3p载荷分量的影响：

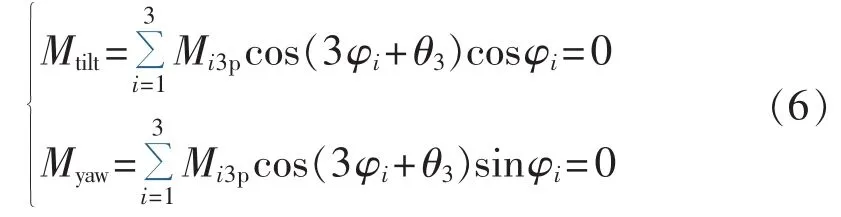
e.叶根拍打弯矩4p载荷分量的影响：

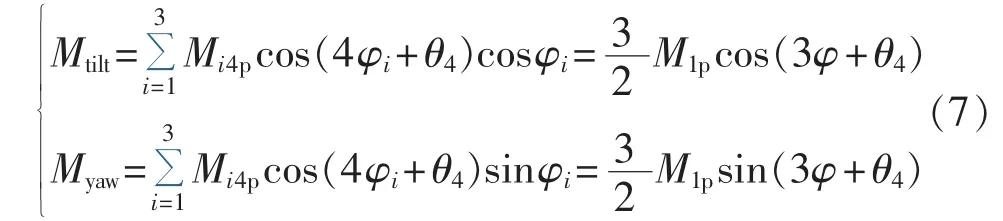
由式（3）—（7）可知，叶根拍打弯矩1p载荷分量会产生倾覆和偏航力矩的直流载荷分量，叶根拍打弯矩2p和4p载荷分量会产生倾覆和偏航力矩的3p载荷分量，而叶根拍打弯矩0p和3p载荷分量则对倾覆和偏航力矩无影响。从载荷控制的角度来看，为减小倾覆和偏航力矩的0p和3p载荷分量，需通过相应控制算法来抑制叶根拍打弯矩的1p、2p和4p载荷分量。

2 直接独立变桨控制策略

为抑制叶根拍打弯矩的1p、2p和4p载荷分量，本文基于高谐波PR控制器，提出了图1所示的直接PR独立变桨控制策略。该控制策略以单个叶片的叶根弯矩为控制变量，通过高谐波PR控制器独立调节每个叶片的桨距角，实现分别减小各叶片叶根弯矩的基波和高次谐波载荷分量的目标。

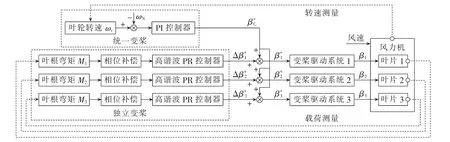
图1 所提直接独立变桨控制策略原理框图Fig.1 Schematic diagram of proposed direct IPC strategy

图中，各叶片的叶根拍打弯矩 Mi（i=1，2，3）可通过传感器装置测量的方法获取。受叶片和变桨驱动系统动态的影响，桨距角给定值与叶根拍打弯矩之间存在较大的相位滞后，为取得更好的控制性能，叶根拍打弯矩测量值Mi进入高谐波PR控制器之前，利用超前补偿器进行相位补偿。超前补偿器的传递函数见式（8），其中α＞1为分度系数，T为时间常数。

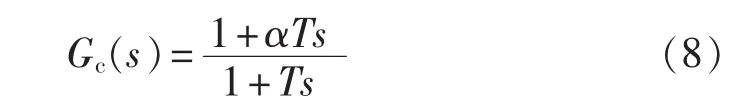
经过相角补偿后的Mi信号作为高谐波PR控制器的反馈输入信号（其给定值分别为0），可产生抑制各叶片载荷的独立变桨偏差角给定信号将其与统一变桨控制策略的输出距角给定信号相加，便可得到每个叶片的最终桨距角给定为抑制Mi的1p、2p和4p载荷分量，高谐波PR控制器采用了图2所示的结构。图中，谐振器R-1p、R-2p和R-4p分别用于消除Mi的1p、2p和4p载荷分量。所采用高谐波PR控制器在s域的传递函数如下：

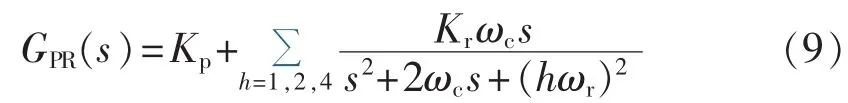
其中，Kp为比例增益系数；Kr为谐振增益系数；ωc为截止频率；hωr（h=1，2，4）为谐振频率。

桨距角最终给定值经过变桨驱动系统便可输出作用于叶片的实际桨距角βi。变桨驱动系统可用式（10）的简单一阶传递函数表示，其中Tp为变桨驱动系统的等效惯性时间常数。

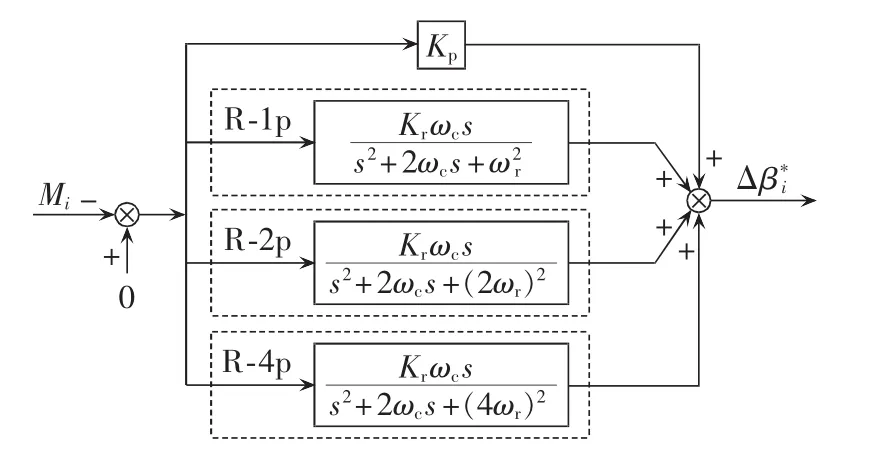
图2 高谐波PR控制器结构框图Fig.2 Schematic diagram of high-order harmonic PR controller

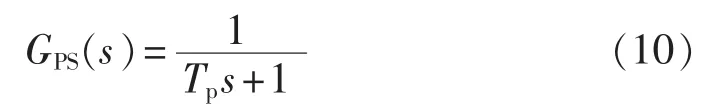
风力机叶片 i（i=1，2，3）的线性模型可用式（11）的桨距角βi至叶根拍打弯矩Mi的传递函数表示［6］：

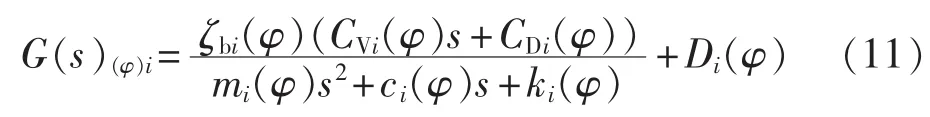
其中，mi（φ）、ci（φ）和 ki（φ）分别为叶片的质量系数、阻尼系数和刚度系数；ζbi（φ）为空气动力对桨距角的输入系数；CVi（φ）和 CDi（φ）分别为叶片拍打波动的位移和速度输出系数；Di（φ）为叶根拍打弯矩对桨距角的输出系数。受重力、风切效应等影响，式（11）的叶片模型参数具有周期时变的特点，模型在不同的叶轮位置角φ处具有不同的参数。

3 控制器参数设计及系统性能分析

控制器参数设计对控制系统运行性能具有重要影响，本节从独立变桨控制系统模型出发，分析了相位补偿器和高谐波PR控制器的参数设计方法，并对控制器的性能进行频率分析。

叶片模型 G（s）（φ）1具有参数时变的特点，在不同叶轮位置角处的叶片线性化模型Bode图如图3所示（G（s）（φ）2、G（s）（φ）3与 G（s）（φ）1频域变化规律相似）。由该图可见，在不同叶轮位置角处，系统的幅值增益和相位增益均有较大差别。

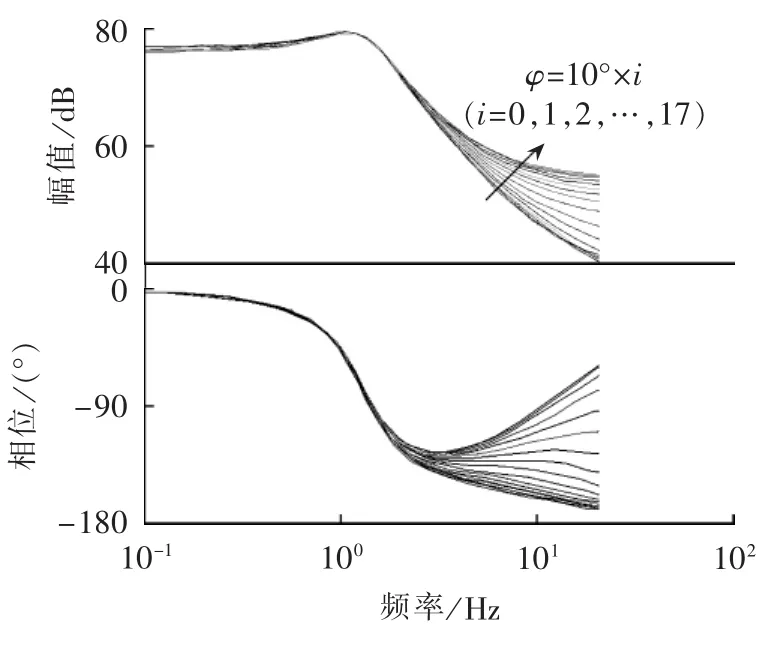
图3 不同叶轮位置角处的叶片线性化模型Bode图Fig.3 Bode diagram of linear blade model for different rotor azimuths

为使控制系统更具鲁棒性，本文将首先对式（11）的叶片线性周期时变模型进行平均化处理，然后在平均化模型的基础上进行控制器参数设计。叶片平均化模型可表示为：

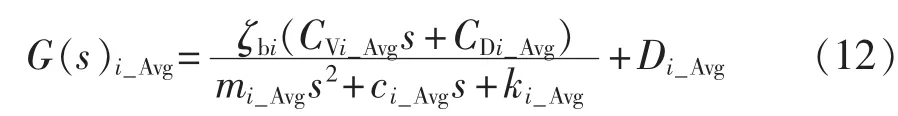
其中，Xi_Avg表示各叶片模型的平均化参数，假设在整个风轮扫略面内共有N个位置角处的线性化模型，则平均化模型的参数为所有模型对应参数的平均值，例如等。

由式（12）所示的叶片平均化模型和式（6）所示的变桨驱动模型容易求出1p、2p和4p频率点处至Mi的相角偏移，然后根据式（13）即可求出式（4）所示相位补偿器的各参数值，式（13）中ωm为补偿点的角频率，φm为对应角频率下的相角偏移量。

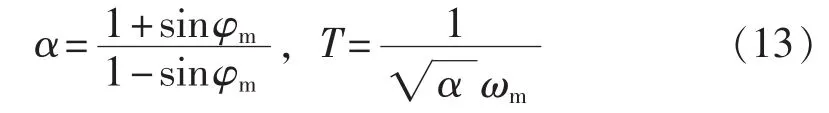
相位补偿前后的平均化系统Bode图如图4所示，可见，经过相位超前补偿，系统在 1p（0.34 Hz）、2p（2×0.34 Hz）和 4p（4×0.34 Hz）频率点处的相移大幅减小。

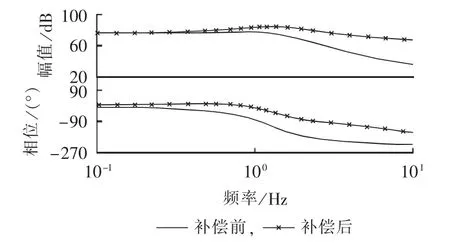
图4 叶片平均化模型和变桨驱动系统模型的Bode图Fig.4 Bode diagram of averaged blade model and pitch drive system model

基于相位补偿后的平均化系统Bode图，利用经典SISO控制理论便可设计出独立变桨高谐波PR控制器参数［15］。PR 控制器包含 Kp、Kr和 ωc3 个参数，各参数的整定方法简单描述如下：首先，PR控制器中参数ωc主要影响系统的带宽，考虑到高风速时，风电机组的转速一般在额定转速ωN的1%左右变化，为了增加控制系统对转速波动的鲁棒性，设计ωc=0.01×ωN；为有效减小系统的载荷稳态跟踪误差，本文在1p谐振频率处的增益根据经验设定为60 dB，则由高谐波PR控制器的传递函数式易于求出Kr的值；控制器参数Kp主要影响系统的稳定裕度和抗扰能力。图5给出了不同Kp值下系统的开环Bode图，由图可见，随着Kp的增加，谐振频率之外系统的幅值增益不断增加，系统的抗扰能力不断减小，然而系统的稳定裕度却经历了先增大后减小的过程，所以Kp的取值应综合考虑系统的稳定性和抗扰能力。

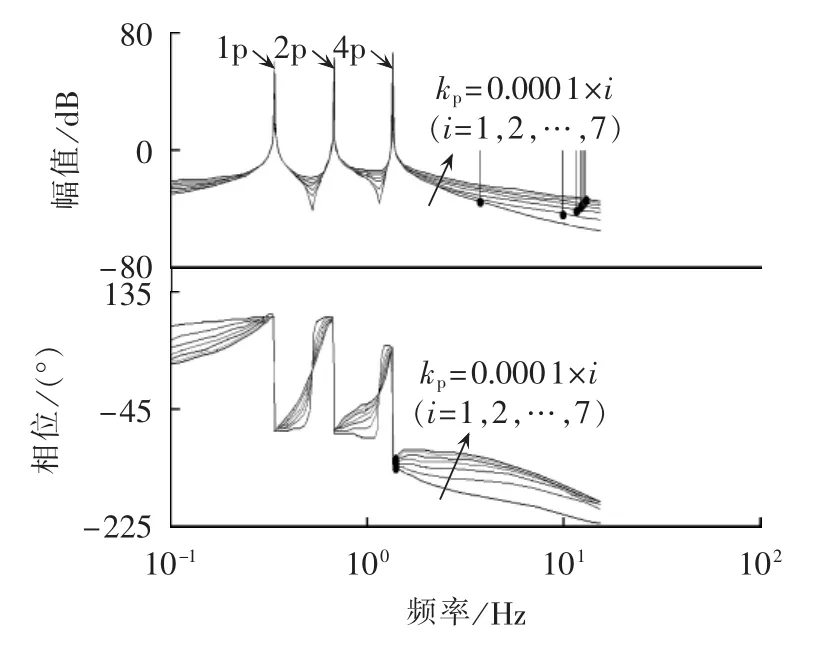
图5 不同Kp下控制系统的开环Bode图Fig.5 Open-loop Bode diagram of control system for different values of Kp

为分析上述基于叶片平均化模型所设计控制器的稳定性、载荷跟踪控制能力，图6和图7分别给出了叶片1的独立变桨控制回路在时变叶片参数下的开环和闭环Bode图（叶片2、3的控制回路与叶片1的控制回路相同）。

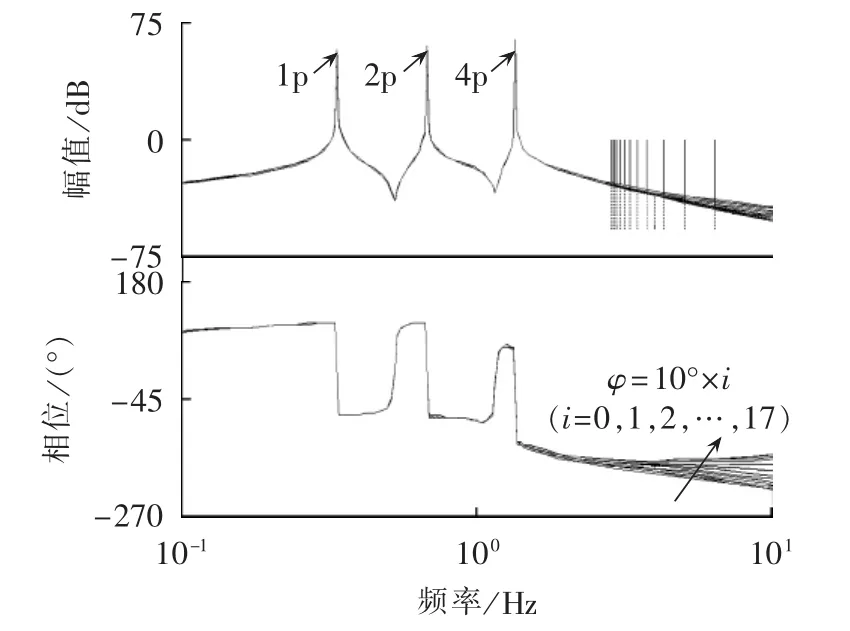
图6 叶片模型参数时变下的控制系统开环Bode图Fig.6 Open-loop Bode diagram of control system for blade model with time-varying parameters

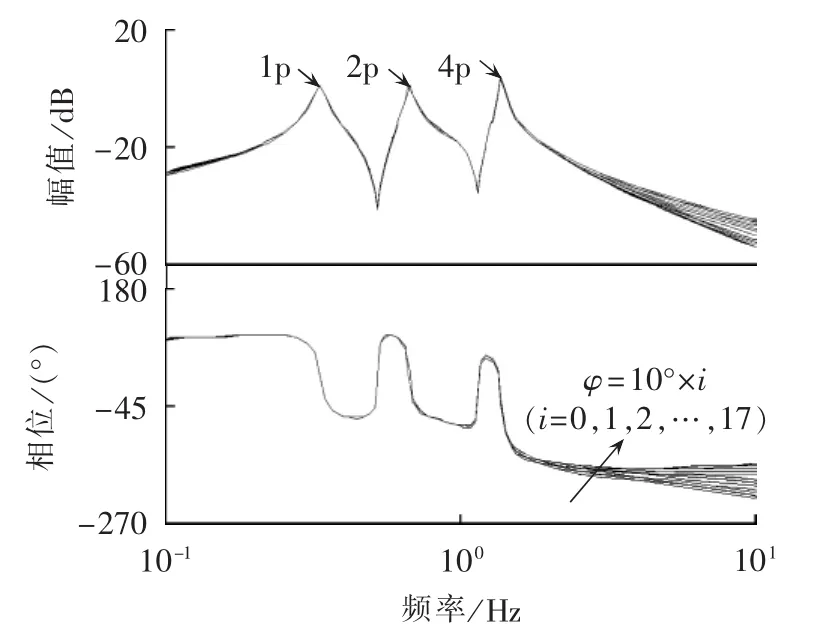
图7 叶片模型参数时变下的控制系统闭环Bode图Fig.7 Close-loop Bode diagram of control system for blade model with time-varying parameters

由图6所示的系统开环Bode图可见，在不同的叶片模型参数下，基于叶片平均化模型设计的控制器参数都能够保证系统具有满意的稳定裕度（相角裕度≈42°，幅值裕度＞20 dB），表明采用叶片的平均线性化模型设计的控制器参数能保证系统具有较好稳定性，控制策略对叶片参数时变具有较好的鲁棒性。

由图7所示的系统闭环Bode图可见，在不同的叶片模型参数下，1p、2p和4p频率点的幅值增益都能保证在0 dB附近，且各频率点处的相移很小，表明闭环控制系统具有较好的载荷跟踪控制能力。

4 仿真验证

为验证所提独立变桨控制策略的有效性，以NREL WP-1.5 MW［16］风电机组为研究对象进行仿真分析。

整个仿真由 NREL 开发的 TurbSim［17］、FAST［16］软件与MATLAB/Simulink组成的风电机组载荷及控制联合仿真系统完成，如图8所示。其中，TurbSim用于标准湍流风速建模，FAST用于风电机组空气动力、结构载荷及简单发电机的建模，而Simulink则用于变桨驱动系统和变桨控制系统建模。利用该联合仿真系统仿真比较了采用所提独立变桨控制策略及采用常规统一变桨控制策略的风力机载荷。

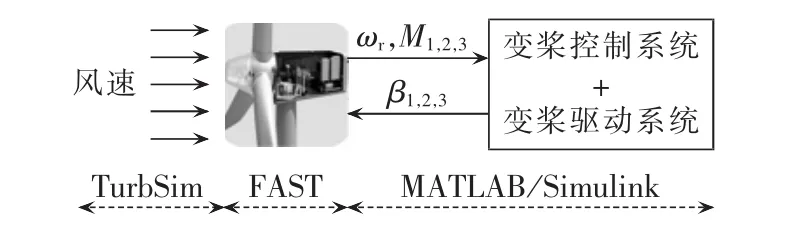
图8 TurbSim-FAST-MATLAB/Simulink风电机组载荷及控制联合仿真系统示意图Fig.8 Schematic diagram of TurbSim-FASTMATLAB/Simulink-based combined load-control simulation model for WTGS

根据第3节的方法，设计出的独立变桨高谐波PR控制器参数为：比例系数Kp=1.1×10-4，增益系数Kr=0.25，截止频率 ωc=0.021 rad/s。

仿真所用IEC61400-1-Ed3［18］标准湍流风速如图9所示，其平均值16 m/s，湍流强度10%，风切系数0.2。

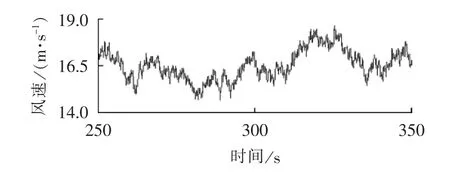
图9 IEC标准湍流风速Fig.9 Wind speed of IEC turbulence

4.1 机组载荷特性分析与比较

图10（a）、（b）分别给出了统一变桨和所提独立变桨控制策略下的叶根拍打弯矩及其功率密度谱。图中，CPC、IPC分别表示常规统一变桨控制策略和所提独立变桨控制策略。由图10（a）可见，采用所提独立变桨控制策略后，叶根拍打弯矩的波动幅度大幅减小；由图10（b）进一步可见，所提独立变桨控制策略几乎能够将叶根拍打弯矩的1p、2p和4p载荷分量消除。

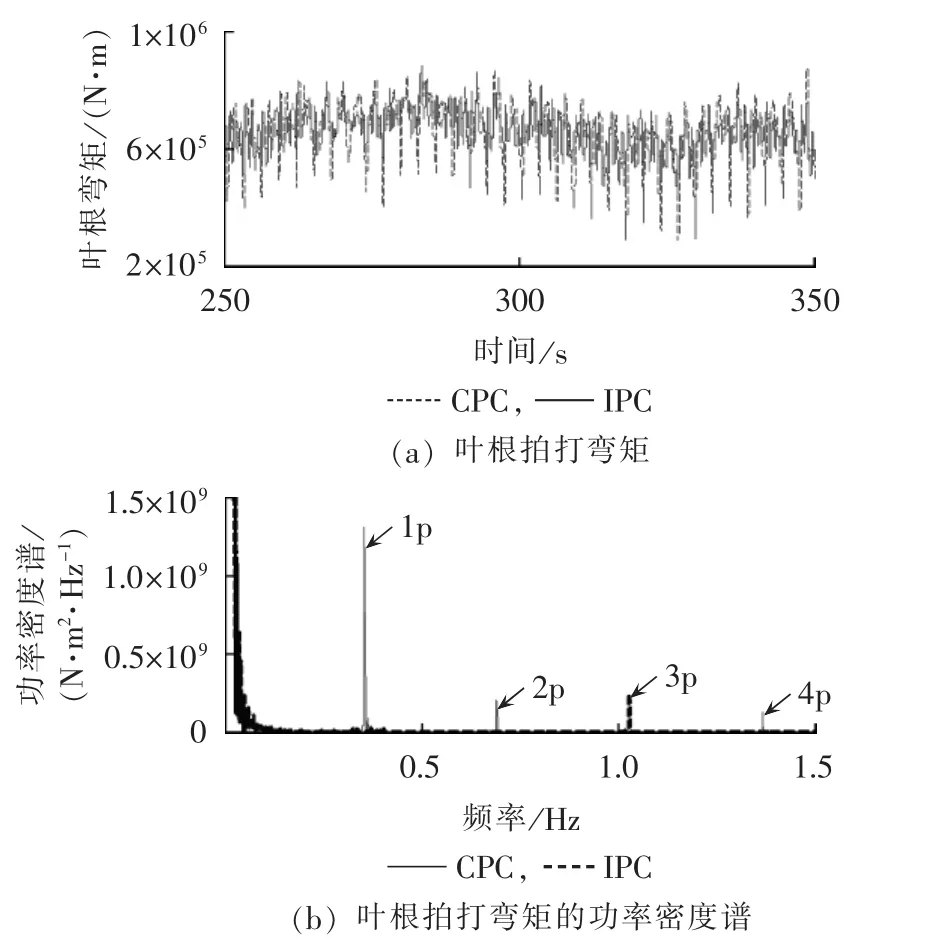
图10 叶根拍打弯矩及其功率密度谱比较Fig.10 Comparison of blade bending moment and corresponding power spectral density

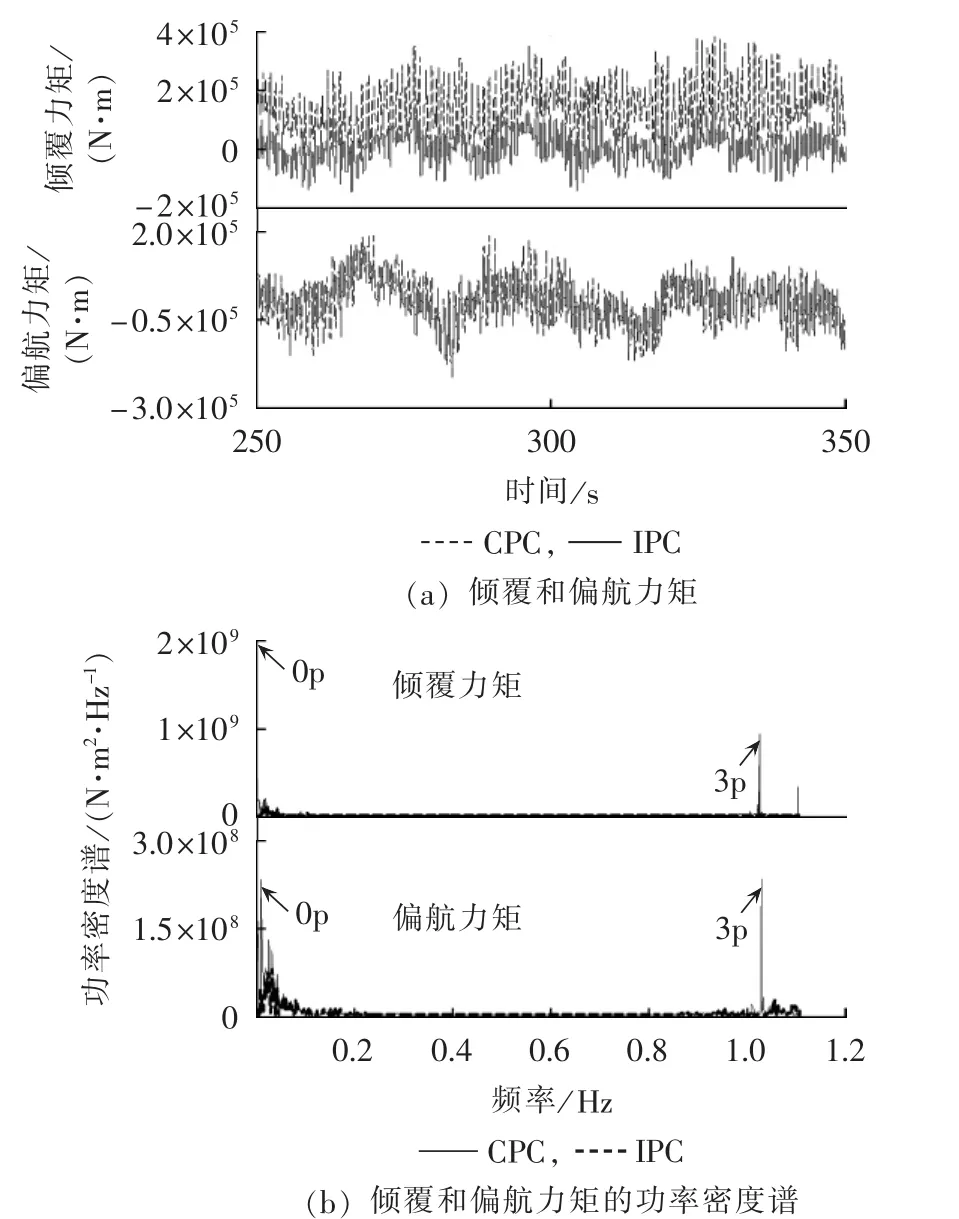
图11 倾覆和偏航力矩及其功率密度谱比较Fig.11 Comparison of tilt and yaw moments and corresponding power spectral densities

图11（a）、（b）分别给出了 2 种变桨控制策略下的倾覆和偏航力矩及其功率密度谱。由图11（a）可见，采用所提独立变桨控制策略后，倾覆和偏航力矩的平均值减小为0 N·m左右，且其波动幅度也大为减小。由图11（b）进一步可知，所提独立变桨控制策略几乎能够将倾覆和偏航力矩的直流载荷分量和3p周期载荷分量完全消除。

为了进一步验证本文提出独立变桨控制策略的载荷抑制效果，本文利用NREL开发的Mlife软件［19］计算比较了2种变桨控制策略下叶根拍打弯矩、倾覆和偏航力矩的1 Hz等值损伤载荷，如图12所示。1 Hz等值损伤载荷，即在对材料疲劳损伤程度相等的条件下，利用周期为1 s且幅值恒定的正弦载荷来等值代替幅值和周期不相等的一组载荷谱［19］。由图可以看出，相比统一变桨控制策略，所提独立变桨控制策略能够将叶根拍打弯矩、倾覆和偏航力矩的疲劳损伤分别减小大约35%、37%和25%。

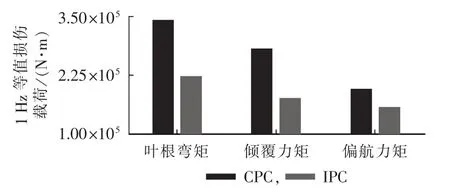
图12 1 Hz等值载荷比较Fig.12 Comparison of 1 Hz equivalent load

4.2 机组运行特性分析与比较

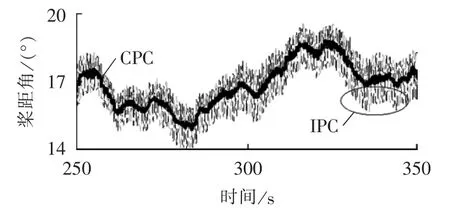
图13 桨距角比较Fig.13 Comparison of pitch angle

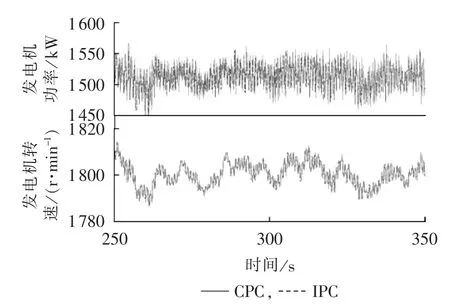
图14 发电机功率、转速比较Fig.14 Comparison of generator power and generator speed

为了进一步分析所提独立变桨控制策略对机组运行特性的影响，图13和图14分别比较了统一变桨和所提独立变桨控制策略下的桨距角、发电机输出功率及转速运行特性。从图13可以看出，采用所提独立变桨控制策略后，3个叶片的桨距角周期性独立动作。从图14可以看出，桨距角的周期性独立动作并未引起发电机输出有功功率及转速的额外波动。

5 结论

本文从减小独立变桨控制系统变量耦合和提高系统鲁棒性角度出发，以单个叶片的叶根弯矩为被控量，提出了一种减小风力机谐波载荷的直接PR独立变桨控制策略。通过建立周期时变叶片系统的平均线性化模型，设计了系统相位补偿器和控制器参数，且对所提控制策略在系统参数时变情况下的稳定性进行了频域分析，并通过建立风电机组载荷及控制联合仿真模型，在IEC标准湍流风速下进一步仿真验证了所提独立变桨控制策略的载荷抑制效果。理论分析和仿真得出如下结论：

a.叶根弯矩谐波载荷分量会对轮毂载荷产生影响，特别是叶根弯矩1p载荷分量会产生倾覆和偏航力矩的直流载荷分量，叶根拍打弯矩2p和4p载荷分量会产生倾覆和偏航力矩的3p载荷分量；

b.通过建立周期时变叶片系统的平均线性化模型，并对所提控制策略的稳定性进行频域分析，结果表明，所提控制策略能很好地跟踪抑制叶根拍打弯矩的1p、2p和4p载荷分量，且具有良好的稳定性和鲁棒性；

c.通过建立 TurbSim-FAST-MATLAB/Simulink风电机组载荷及控制联合仿真模型，仿真比较常规统一变桨控制策略和所提独立变桨控制策略下机组的载荷特性，结果表明，所提直接独立变桨控制策略能够将叶片的1p、2p和4p及轮毂的0p和3p周期载荷分量基本消除，能够将叶片和轮毂的疲劳损伤大幅减小，且所提独立变桨控制策略虽然使得桨距角运行更为频繁，但桨距角的周期性独立调节并未引起机组输出有功功率和转速的额外波动。

［1］龚文明，胡书举，许洪华.一种适用于大型风电场实时仿真的双馈风力发电机响应模型［J］. 电力自动化设备，2014，34（4）：114-119.GONG Wenming，HU Shuju，XU Honghua.Response model of DFIG for real-time simulation of large-scale wind farms［J］.Electric Power Automation Equipment，2014，34（4）：114-119.

［2］肖帅，杨耕，耿华.抑制载荷的大型风电机组滑模变桨距控制［J］.电工技术学报，2013，28（7）：145-150.XIAO Shuai，YANG Geng，GENG Hua.Sliding-mode pitch control strategy for large wind turbines to reduce loads［J］.Transactions of China Electrotechnical Society，2013，28（7）：145-150.

［3］BARAHONA B，CUTULULIS N A，HANSEN A D，et al.Unbalanced voltage faults：the impact on structural loads of doubly fed asynchronous generator wind turbines［J］.Wind Energy，2014，17（8）：1123-1135.

［4］BOSSANYI E A.Individual blade pitch control for load reduction［J］.Wind Energy，2003，6（2）：119-128.

［5］应有，许国东.基于载荷优化的风电机组变桨距控制技术研究［J］.机械工程学报，2011，47（16）：106-111.YING You，XU Guodong.Developmentofpitch controlfor reduction on wind turbines［J］.Journal of Mechanical Engineering，2011，47（16）：106-111.

［6］van ENGELEN T.Design model and load reduction assessment for multi-rotational mode individual pitch control（higher harmonics control）［C］∥European Wind Energy Conference.Athens，Greece：2006，ECN：27.2-2.3.

［7］BOSSANYI E A，FLEMING P A，WRIGHT A D.Validation of individual pitch control by field tests on two-and three-bladed wind turbines［J］.IEEE Transactions on Control Systems Technology，2013，21（4）：1067-1078.

［8］GEYLER M，CASELITZ P.Robust multivariable pitch control design for load reduction on large wind turbines［J］.Journal of Solar Energy Engineering，2008，130（3）：1-10.

［9］KAUSIHAN S.Individual pitch control for large scale wind turbines［D］.Delft，Holland：TU Delft，2007.

［10］STOL K A，MOLL H G，BIR G，et al.A comparison of multiblade coordinate transformation and direct periodic techniques for wind turbine control design［C］∥Proceedings of the 47th AIAA/ASME.Orlando，USA：AIAA，2009：1-12.

［11］SELVAM K，KANEV S，van WINGERDEN J W，et al.Feedbackfeedforward individual pitch control for wind turbine load reduction ［J］.International Journal of Robust and Nonlinear Control，2009，19（1）：72-91.

［12］LU Q，BOWYER R，JONES B L.Analysis and design of Coleman transform-based individualpitch controllersforwind-turbine load reduction［J］.Wind Energy，2014，17（9）：1301-1467.

［13］ZHANG Y，CHEN Z，CHENG M.Proportional resonant individual pitch control for mitigation of wind turbines loads ［J］.IET Renewable Power Generation，2013，7（3）：191-200.

［14］PAN T，MA Z.Wind turbine individual pitch control for load reduction based on fuzzy controller design［J］.Proceedings of the Institution of Mechanical Engineers，Part I：Journal of Systems and Control Engineering，2013，227（3）：320-328.

［15］CHA H，VU T K，KIM J E.Design and control of proportionalresonant controller based photovoltaic power conditioning system［C］∥Proceedings of the IEEE Energy Conversion Congress and Exposition.San Jose，CA，USA：IEEE，2009：2198-2205.

［16］JONKMAN J M，Jr BUHL M L.FAST user’s guide［R］.Golden，CO，USA：National Renewable Energy Laboratory，2005.

［17］JONKMAN B J.TurbSim user’s guide：version 1.50［R］.Golden，CO，USA：National Renewable Energy Laboratory，2009.

［18］IEC.Wind turbines，part 1：design require-ments：IEC61400-1-2005［S］.Geneva，Switzerland：International Electrotechnical Commission，2005.

［19］HAYMAN G J.MLife theory manual for version 1.00 ［R］.Golden，CO，USA：National Renewable Energy Laboratory，2012.