基于MAS和CA的多微电网孤岛模式下无功电压的控制

鲁 斌，刘雪艳

（华北电力大学 计算机系，河北 保定 071003）

0 引言

在近几年世界范围内接连几次发生大面积停电事故和自然灾害以后，大电网的脆弱性充分地暴露出来，大电网成本高，运行难度大，难以满足用户越来越高的安全性和可靠性要求［1］。

随着能源瓶颈现象日益凸显，微电网作为新型能源在中国发展，而对于多微电网的无功电压控制的研究具有极大的紧迫性［2］。微电网的无功和有功电压出力的稳定，将直接影响多微电网的母线电压和频率，进而使系统稳定。然而，随着微电网技术的不断推广应用，如何妥善管理微电网内部分布式电源和储能的运行，实现微电网经济、技术、环境效益的最大化成为重要的研究课题［3］。

由于微电网内能源结构、分布式电源类型和控制方式的多样性，微电网的能量管理和优化运行具有较高的复杂性［4-5］。同时，考虑微电网本身的多目标属性，传统的以大型发电机为主的单目标调度优化方法难以适应复杂的微电网环境［6］。集中控制和分散控制相结合的方式将取代原有的统一调度方式，成为微电网控制的最佳手段之一。但目前在多微电网控制方面的研究还有待深入。

文献［7］提出了将多代理系统MAS（Multi Agent System）应用于孤岛模式下电力系统的无功电压的控制中，但现有研究还未涉及不同运行状态下多个微电网之间的协调控制，这对于多微电网的正常运行和本地负荷的可靠供电至关重要。文献［8］对微电网接入主动配电网后的网架结构、规划设计、控制方案、运行模式、综合效益等问题进行了阐述，分析了应用微电网技术为主动配电网带来的优势，但没有阐述微电网应用于主动配电网的具体措施。文献［9］验证其所提暂态电压稳定协同控制策略能有效增强微电网的电压稳定性，但是文章所提方法是否具有广泛适用性仍有待考究。文献［10］提出了多微电网分层孤岛设计模式，但没有对子微电网之间的具体协调控制策略进行描述。

现阶段元胞自动机CA（Cellular Automata）模型多应用于研究交通、农村土地格局优化、金融以及工业生产等，在电力系统方面的应用尚在起步阶段，而在微电网中的应用则更少，CA因其自身的灵活性应用于微电网中将具有一定的优势。文献［11］运用多智能体和CA相结合来模拟城市用地扩张的方法，将影响和决定用地类型转变的主体作为Agent引进CA模型中，Agent在CA确定的城市发展概率的基础上，决定元胞下一时刻的城市发展概率。文献［12］提出了一种将Fisher判别方法和CA理论结合后应用于微电网格局计算的方法，用来制定微电网元胞空间的总体演化规律。文献［13］根据CA的基本理论及其在城市动态演化模拟中的应用，提出了新的电力负荷空间分布预测方法。文献［14］提出一种基于Fisher判别和离散选择模型相结合自动获取地理CA转换规则的方法，但没有涉及元胞之间的具体作用。文献［15］提出了一种基于MAS和CA的“自下而上”的微电网分布式协调控制模型以及微电网自趋优控制策略，但没有涉及CA和MAS模型在多微电网中的应用。文献［16］提出了基于虚拟功率的下垂控制法，通过把实际有功功率和无功功率转换成虚拟功率，对传统下垂控制法进行修正。但文献［17］指出了其缺陷并提出了基于虚拟频率-电压的下垂控制法，然而这种方法要求并联逆变器具有相同的转换角，实现难度大。

本文考虑了微电网孤岛模式下的无功电压控制，创新性地提出了孤岛模式下基于MAS和CA的多微电网无功电压控制策略，构建了基于MAS和CA的微电网分布式协调控制模型，并在此基础上进行了仿真，验证了该方法可以有效地调节微源的有功和无功出力情况以及系统的母线电压和频率，维持系统的稳定运行。

1 多微电网系统无功电压控制

1.1 微电网孤岛运行无功电压特点

孤岛运行时，由于缺少外部大电网的电压和频率的支撑，微电网的频率控制具有一定的挑战性。此时，微电网的负荷全部由分布式电源提供［1］。这就需要微电网自身保持其内部电能的供求平衡，还需要保证电压和频率的相对稳定，但是微电网自身的调节能力不一定满足负荷的要求。若负荷波动较大，则微电网很难实现对电压的调节，甚至会出现电压崩溃的情况；若微电网的调节能力能够满足负荷变化的要求，但负荷变化特别是无功负荷的变化也可能会引起电压较大的波动。所以在孤岛运行模式下，要综合考虑负荷变化以及微电网自身的调节能力［2］。当多微电网中的某子微电网处于孤岛模式，并难以实现本身电能的供需平衡时，其与其他的子微电网之间是否存在交互、如何维持母线电压以及输出频率的稳定，这在目前是十分有必要研究的。

为了解决这一问题，本文构建了基于MAS和CA的多微电网分布式分层协调控制模型，来跟踪孤岛模式下多微电网的无功电压输出、各子微电网的无功电压输出情况以及在某个子微电网出现故障时其他子微电网之间对于协调多微电网总体稳定的处理情况。

1.2 微电网无功电压的数学模型

对于任意一个多微电网的子网，子网内每个节点处的无功功率平衡方程为［7，18］：

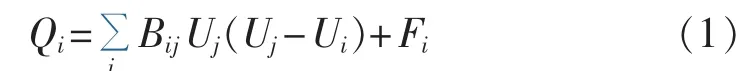
其中，Bij为节点i和j之间的互导纳；Ui和Uj分别为节点i和j的电压；Fi为相邻微电网注入节点i的无功电压潮流，本文中不考虑多微电网子网之间的彼此影响，令Fi=0。

使用向量形式表示所有负载和发电机向量在该地区的利益，得到：

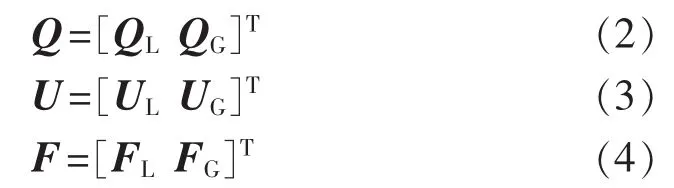
则方程（1）可以写成：

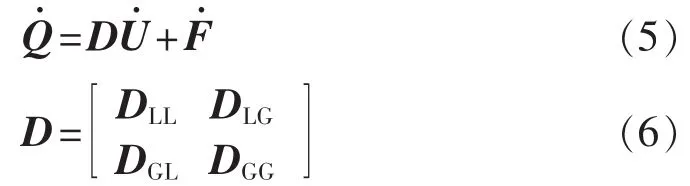
其中，D为灵敏度矩阵，即潮流方程雅可比矩阵中与电压、无功功率相关的部分，DGG为微电源馈线之间的互导纳，DGL和DLG分别为微电源馈线和负荷馈线之间的互导纳，DLL为负荷馈线之间的互导纳。因此线性化系统模型可用如下灵敏度方程表示为（假定F=0）［14］：

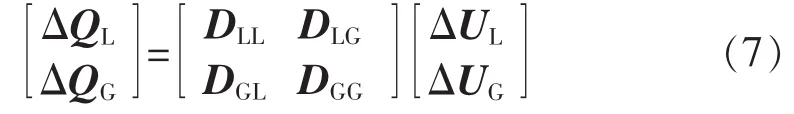
其中，ΔUL为负荷电压变化值；ΔUG为微电源电压变化值；ΔQL为负荷无功功率变化值；ΔQG为微电源无功功率变化值。

若令则式（7）可简化为：

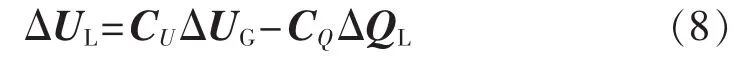
其中，CUΔUG为对负荷节点电压的影响；CQΔQL为无功扰动引起的负荷节点电压变化值。式（8）也是对负荷Agent计算电压偏差值的表达式。

2 基于MAS和CA的双层多微电网分布式协调控制模型

2.1 MAS说明与构建

多个结构和性能较为简单的Agent组成一个结构较为松散的MAS［19］。在MAS中每个需要完成的任务对于一个Agent而言是透明的，每个Agent只拥有部分功能权限和信息资源，如果各个Agent之间无法进行通信联系来协调，将无法解决实际问题，这就是群体共同解决问题的流程，如果只是单个Agent来负责，无法解决如此繁复的任务。目前来看，MAS的解决方案正被广泛应用于各个领域。随着MAS应用领域的扩展，MAS的智能化水平越来越高，解决实际复杂问题的能力越来越强。

微电网为典型的分布式系统，MAS可以提高其分布式电源之间、分布式电源与负荷之间以及微电网之间的协调控制。

MAS模型中的每一个Agent都可以代表一个实体或一种决策过程，并且Agent具有自治、通信、可协调等特点。MAS中的Agent之间相互影响，它们一方面根据运行情况自主完成特定的调压任务，另一方面可通过通信系统与同级Agent之间分享信息，接收上级Agent下达的调压任务并反馈执行情况，实现系统的整体协调，达到维持微电网电压水平的目的［12］。 本文中主要运用 4种Agent：电网 Agent（PCC Agent）、微电网 Agent（microgrid Agent）、当地控制 Agent（LC Agent）、微源 Agent。

电网Agent的主要功能是提供大电网与微电网的接口，通过该接口可以实现微电网与大电网的并网运行状态和微电网孤岛运行状态的切换；同时大电网可以通过电网Agent向微电网下达命令。

微电网Agent的主要功能是对当地控制Agent的监控与管理。一方面，微电网Agent获取来自各当地控制Agent的信息，对各区域进行监控和管理；另一方面，微电网Agent负责组织和管理当地控制Agent，接收大电网的命令。

当地控制Agent的主要功能是对当地的微源Agent和负荷单元进行管理。一方面，当地控制Agent对微源Agent和负荷单元进行管理，执行控制策略；另一方面，它负责接收微电网Agent发来的命令及向其发送反馈信息。

微源Agent的主要功能是对当地的微源进行管理，存储微源（光伏电池组、风力发电机、微型燃气轮机等）的相关信息（额定功率、分布式能源种类、可增发负荷等），并监测微源的功率输出情况和运行状态，转换微源的控制方式等；与其他微源Agent进行通信；接收上级当地控制Agent的命令。

微电网中，各Agent之间的交互情况如图1所示。

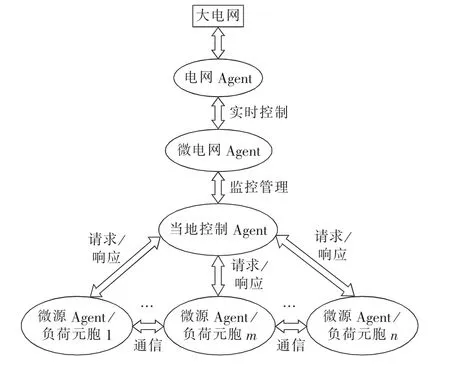
图1 各Agent之间的交互情况Fig.1 Interaction among Agents

2.2 CA简介

CA是一种通过简单的局部运算模拟空间上离散、时间上离散的复杂性现象的模型［7］。元胞以某种离散状态分布于规则网格中的任意地方，并且以相同的规则进行状态更新，它们通过简单的相互作用来形成一个动态的系统。CA包括元胞及状态、元胞空间、邻居以及转换规则，其模型如图2所示［12］。

元胞是CA的基本元素，通常情况下元胞以0、1这2种状态存放元胞状态集，元胞空间是元胞所处的空间网格的集合。CA中的邻居作用于当前元胞状态，使之在直接相邻元胞范围发生状态转变。二维的CA邻居有Moore型、冯诺依曼型以及扩展Moore型，其中Moore型比较常见。本文CA模型中的邻居采用 Moore 型，其定义为［12］：

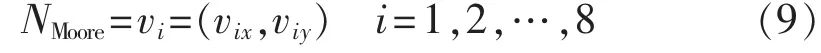
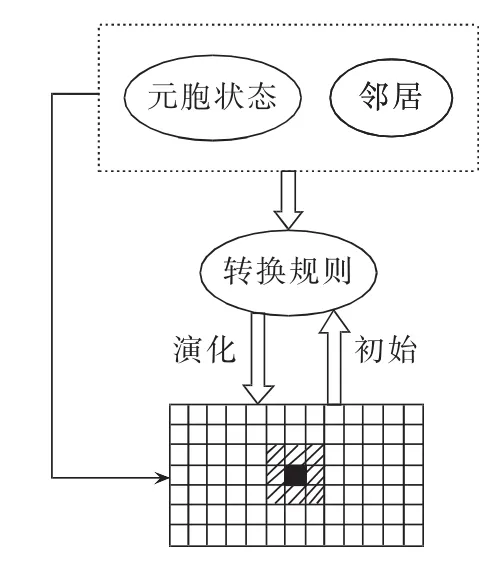
图2 CA模型Fig.2 Model of CA

其中，代表二维元胞空间；vi为邻居元胞；（v0x，v0y）为中心元胞的坐标；（vix，viy）为邻居元胞的坐标。

而CA的演化规则指元胞根据自己当前的状态及其邻居的状态来确定下一时刻状态的函数。该函数考虑了这个元胞所有状态和这些状态的变换规律，构造成一种简单、离散的局部变换模型。由此可定义 CA 模型如下［12］：

其中，f为CA演化规则；t为时间；为t时刻元胞i的状态；为元胞邻居状态组合；为t+1时刻元胞i的状态。

2.3 基于MAS和CA的双层协调控制模型

本文中构建了一种基于MAS和CA的双层架构模型结构，然后用它来建立“由下而上”的多微电网分布式协调控制模型。

上层模型通过微电网中的Agent之间的交互信息来实现微电网分布式协调控制功能；下层模型基于CA建模，用来监测并描述微电网中微源和负荷的参数变化情况以及孤岛模式下各子微电网之间的协作状况。下层模型不断地为上层模型提供制定优化控制策略所需要的基础数据，并根据上层模型提供的控制策略改变自己的行为；上层模型根据下层模型提供的数据通过交互操作来制定优化控制策略，并指导下层模型的行为［15，20］。该双层模型中 MAS 部分由图2中涉及的4种Agent之间的交互组成，因此本文所构建的基于MAS和CA模型的多微电网分布式协调运行双层框图如图 3所示［14］。

3 基于MAS和CA的多微电网无功电压控制

常见的分布式电源有2类：微型燃气轮机、燃料电池是一类功率可调的机组，并网运行时采用P/Q控制，而在各子微电网孤网运行时，为调节系统的安全稳定性，采用U/f控制；风电、光伏发电是间歇性的，受风和光等因素的影响较大，采用P/Q控制。

在2.1节中提到微电网可以通过电网Agent实现与大电网的互连和断开状态的切换，这样只要通过监测PCC处的电力参数即可确定微电网在下一时刻的连接状态，从而确定微电网是否处于孤网状态。可以通过观测微电网的孤岛电压限值实现，微电网孤岛电压限值如表1所示［15］。

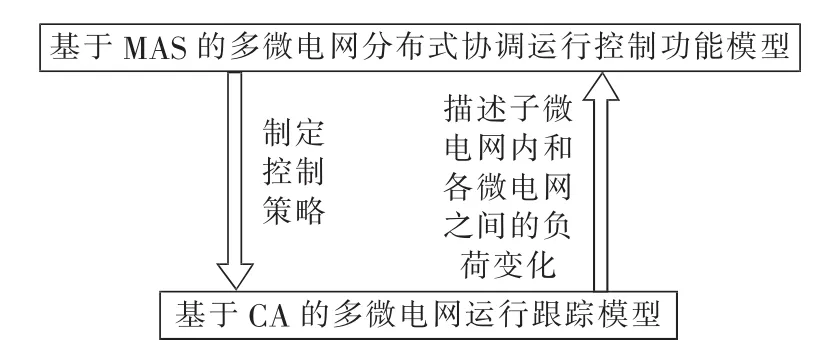
图3 基于MAS和CA模型的双层架构框图Fig.3 Block diagram of dual-layer model based on MAS and CA

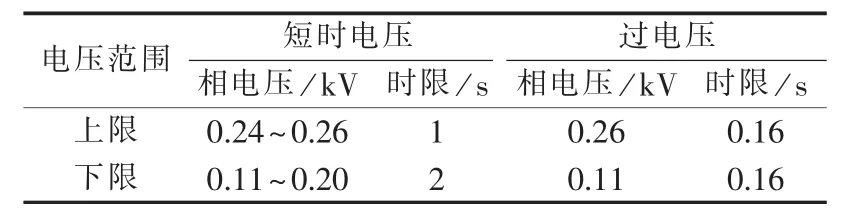
表1 孤岛电压限值Table 1 Voltage limits of isolated microgrid

本文结合3.2.1节中所讲述的CA的特性，将微源和负荷抽象成微电网中的元胞，它们的集合构成了一个元胞空间；用元胞规则来模拟各元件的运行情况；给每个元胞赋一定的初值，这样就可以建立起用CA来模拟微源和负荷运行的子微电网以及子微电网之间的运行跟踪模型。

根据元胞的频率变化值Δf和电压变化值Δu是否超过频率和电压控制范围来判断当前元胞的状态。元胞超过范围就会出现故障，此时元胞状态值置为“1”；若在控制范围内，则已经处于正常运行状态或元胞可以经过微调恢复正常状态，此时元胞状态值置为“0”。我国采用的额定频率为50 Hz，正常运行时应当保持在（50±0.2）Hz的范围之内；用户供电电压的允许偏移量对于10 kV及以下电压等级为±7%，微电网由380 V～10 kV供电电压组成，本文模型假设按380 V供电，因而电压允许偏差应不超过20～25 V［21］。

孤岛模式下，微源元胞输出功率与负载吸收功率的能量守恒方程为［17-18］：

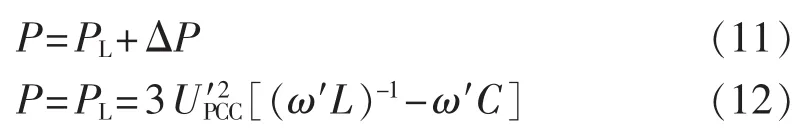
其中，ω′=ω+Δω 为孤岛模式下公共连接点（PCC）处的角频率；ω 为 PCC 处的角频率；U′PCC=UPCC+ΔUPCC为孤岛模式下PCC处的相电压，UPCC为PCC处的相电压；P为微源输出的有功功率和无功功率；PL为负荷吸收的有功功率和无功功率；ΔP为多余的有功功率和无功功率。

当多微电网处于正常运行状态下，电网Agent、微电网Agent和微源Agent/负荷元胞都处于监测状态，电网Agent监测大电网PCC处的相电压，微电网Agent监测大电网的母线电压、各负荷节点电压变化情况，而微源Agent监测本地的频率和线路电压变化值。根据负荷节点电压是否越限可以判断微电网是否进入紧急情况。控制策略步骤如下［15］。

（1）当电网Agent监测到大电网PCC处的相电压超出孤岛电压限值时，电网Agent将大电网的断路器断开，此时多微电网进入孤岛状态。

（2）微源Agent/负荷元胞周期性地监测本地电压频率和变化值，并将该值实时传送给当地控制Agent。

（3）当地控制Agent判断负荷元胞发送来的频率和电压变化值是否在故障范围内，若不在故障范围内，则当地控制Agent继续实时接收来自负荷元胞的反馈信息；若在故障范围内，则判断通过调节电压控制器是否可以消除电压越限，如果可以，则命令电压控制器来调节负荷电压值，否则当地控制Agent向微电网Agent发出调压请求。

（4）微电网Agent收到调压请求后命令相应的微源Agent/负荷元胞调节电压值来消除越界。

（5）微源Agent/负荷元胞判断通过自身调节是否可以消除越界，若可以，则自行调节电压值，否则立即向微电网Agent发出协助调压请求。

（6）微电网Agent收到请求后，选择需要协助调压的微源Agent/负荷元胞，若能发现这种Agent，则继续步骤（7），否则跳至步骤（9）。

（7）微源Agent/负荷元胞收到微电网Agent发出的调压命令后，要判断协助调压是否会对自身电压值造成干扰，若不会，则进行协助调压，否则拒绝执行调压。协助调压的微源Agent/负荷元胞在完成任务后要向微电网Agent反馈信息。

（8）微电网Agent收到反馈信息后，判断电压越界是否消除，若消除，则将该信息发送给请求协助调压的微源Agent/负荷元胞，跳至步骤（10），否则继续步骤（9）。

（9）微电网Agent根据负荷元胞相对于微电网的重要程度来选择需要切除的负荷，并命令相应的当地控制Agent断开连接；当地控制Agent收到断开连接的命令后，将断路器的连接状态置为“0”（“0”代表断开状态，“1”代表连接状态），并向微电网Agent反馈信息，跳至步骤（8）。

（10）微源Agent/负荷元胞收到电压越限消除的消息后，再次检测电压的状态，若电压恢复正常，则向协助调压的微源Agent/负荷元胞发出确认信息，否则跳至步骤（5）。

（11）此时大电网的故障消除，3 s后，微电网Agent向被切掉负荷的当地控制Agent发送重新接入微电网的命令，其将断路器的连接状态置为“1”，重新接入微电网。

（12）大电网故障消除后，会向电网Agent发送故障已消除的信息。电网Agent会将各孤岛模式下的子微电网重新接入大电网，恢复并网状态。系统此时可能需要重新加以调节，跳至步骤（1）。

当微电网的某子微电网发生故障时，会自行切断断路器，以保证大电网母线及其他子微电网的安全运行。而此时大电网中的其他子微电网会承担调节母线电压及频率的任务。若母线电压无法稳定，则必须切除不必要的负荷来维持电压的稳定。

4 系统建模与仿真

4.1 系统仿真模型

本文研究的多微电网由3个可孤岛运行的子微电网构成。当孤岛运行时，每个子微电网相当于一个单独的供电系统，而孤岛模式下子微电网是存在相互影响的。该仿真模型中包含着2.1节中所述的4 种类型的 Agent（电网 Agent、微电网 Agent、当地控制Agent以及微源Agent）。其中子微电网A包括微型燃气轮机（MT）和光伏电池组（PV）；子微电网B包括燃料电池（FC）和风力发电机组（WD）；子微电网C包括光伏电池组和风力发电机组。用PSCAD构建仿真模型如图4所示（本仿真模型中暂不考虑导线电阻及其在传输过程中的损耗）。其中，DMS代表配电网调度系统；MV代表控制电压；LV代表低电压；MC表示人工控制；LC表示负荷中心。

根据分布式电源的参数范围，本文模型中各微源元胞的参数如表 2 所示［1，22］。

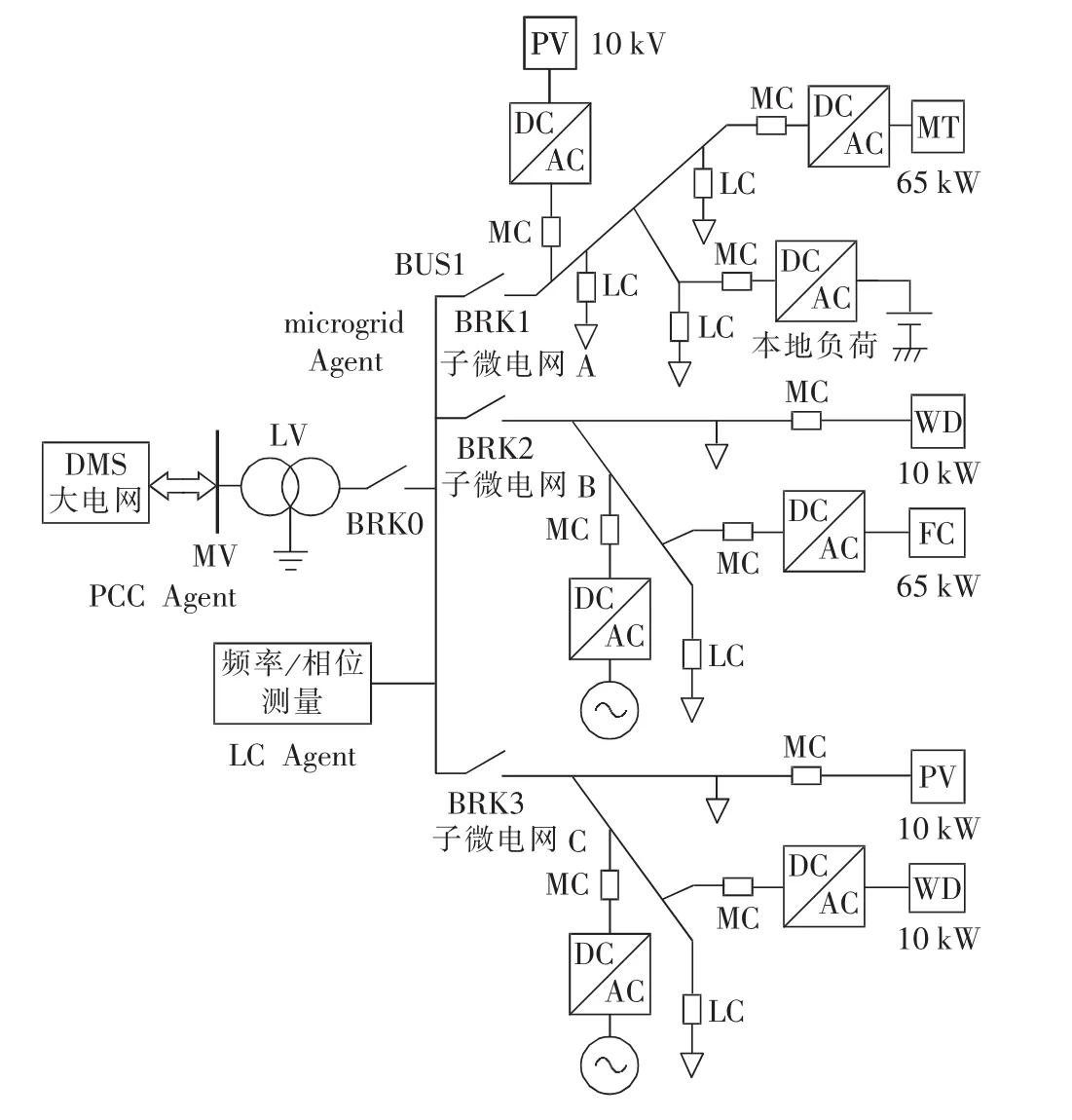
图4 多微电网仿真模型简图Fig.4 Sketch of multi-microgrid simulation model

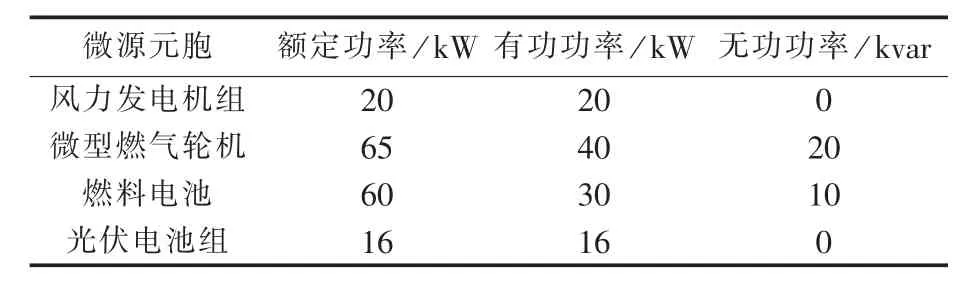
表2 微电源参数表Table 2 Parameters of micro-sources

4.2 算例仿真分析

根据2.2节中所述的微电网无功电压数学模型，结合CA监测的电压和频率的变化值，判断系统是否可以正常运行，进行孤岛模式下多微电网的无功电压控制仿真实验。本文主要考虑光照、风速以及某个子微电网故障对多微电网及子微电网之间的影响。仿真时开关BRK0断开，各子微电网进入了孤岛模式。假定仿真时间为10 s。

4.2.1 光照强度改变对各微电网的影响

开始时光照强度是600 W/m2，第3 s时增大至800 W/m2，第 6 s时光照强度恢复到 600 W /m2，仿真结果如图 5— 7 所示。其中，QMT、QFC、QWD、QPV分别为微型燃气轮机、燃料电池、风力发电机组、光伏电池组输出的无功功率；Ubus为母线电压有效值（标幺值）；fs为系统频率。

由图5可知，光伏电池在光照强度为600 W/m2时，微型燃气轮机输出的无功功率上升为20 kvar，燃料电池输出的无功功率上升为10 kvar，风力发电机无功功率维持在0 kvar，光伏电池无功功率为0 kvar；第3 s时，光照强度由 600 W/m2增加至 800 W/m2，光伏电池无功出力稳定在0 kvar，微型燃气轮机和燃料电池无功出力维持不变；第6 s时，光照强度回到600 W/m2，微型燃气轮机和燃料电池的无功功率仍维持不变。

由图5—7可知，在光照强度发生变化时，子微电网A在微型燃气轮机的调节下，其母线电压基本维持不变；子微电网B在燃料电池的调节下，其母线电压基本维持不变；子微电网C中的光伏电池和风力发电机的无功功率输出为0；系统频率在光照强度发生变化时有微小波动，但是频率改变值维持在（50±0.02）Hz内，能够满足微电网运行要求。

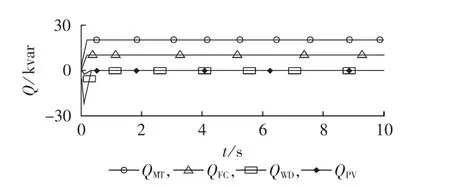
图5 光照强度改变时各微源元胞输出无功功率Fig.5 Output reactive powers of micro-source cellular when light intensity changes

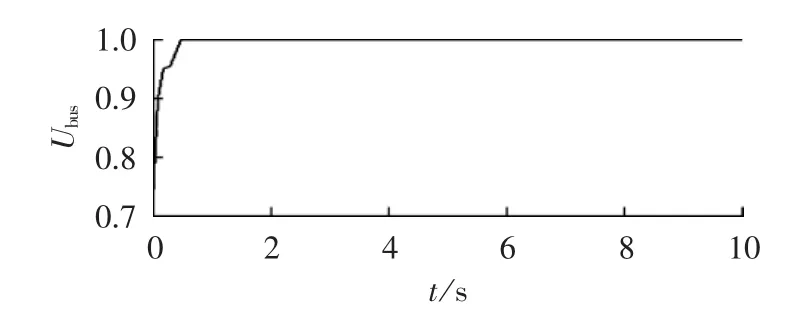
图6 光照强度改变时母线电压有效值Fig.6 Effective value of bus voltage when light intensity changes

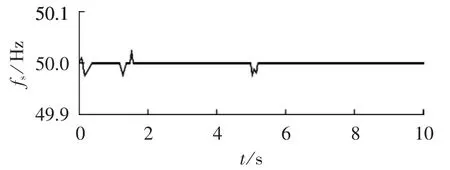
图7 光照强度改变时系统频率Fig.7 System frequency when light intensity changes

由上述结论可知，无功功率和母线电压在光照强度发生变化时基本不变，系统频率在允许的范围内有较小的波动，各微源对无功电压的控制取得了较好的效果。因此，子微电网A中的微型燃气轮机不仅对自身电压起调节作用，还对子微电网B和C起到了良好的调节作用，使得多微电网整体功率相对平稳。

4.2.2 风速变化对各子微电网的影响

实验采用随机风速，光照强度保持在800 W/m2，仿真时间为10 s，仿真结果如图8—10所示。

由图8—10可知，风速增大时风力发电机的无功输出增多，风速减小时风力发电机的无功输出减少，且其无功输出在0 kvar上下波动；微型燃气轮机输出的无功功率在23 kvar上下波动；燃料电池输出的无功功率在15 kvar左右波动；光伏电池无功输出恒为0 kvar。多微电网母线电压在1.0 p.u.左右波动，系统频率在50 Hz左右小范围波动，满足系统最低要求。

由以上分析可知，孤网模式下，随风速的变化，为了维持多微电网系统无功出力的平衡，子微电网A中微型燃气轮机对调节子微电网B和子微电网C起到了良好的作用，多微电网中的各微源无功电压在允许的范围内波动，使母线电压和系统频率相对平衡。

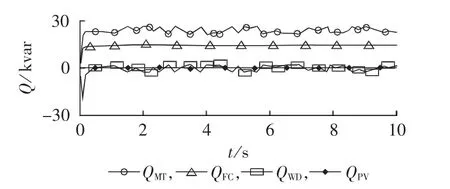
图8 风速变化时各微源元胞输出无功功率Fig.8 Output reactive powers of micro-source cellular when wind speed changes

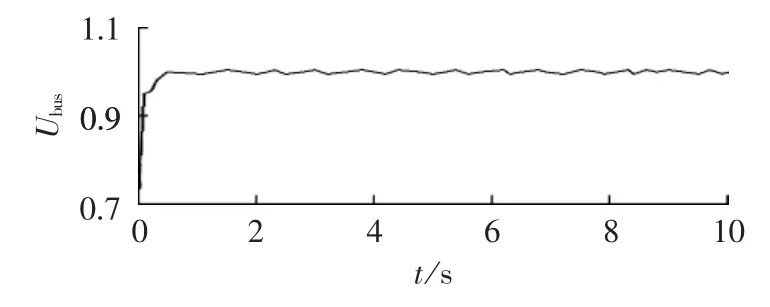
图9 风速变化时母线电压有效值Fig.9 Effective value of bus voltage when wind speed changes

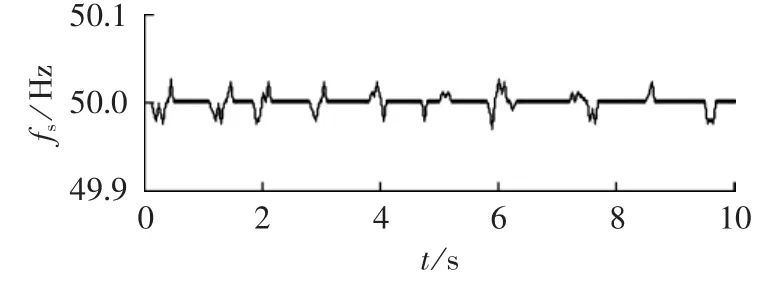
图10 风速变化时系统频率Fig.10 System frequency when wind speed changes

4.2.3 燃气轮机和光伏电池组（子微电网A）故障对多微电网的影响

开始时，各子微电网在孤网模式下各自平稳运行，在第5 s时将子微电网A与母线连接的开关BRK1断开，来模拟燃气轮机和光伏电池组故障，仿真时间10 s，仿真结果如图11—13所示。

由图11可知，在0～5 s内，微型燃气轮机和风力发电机波动较大，且其无功输出分别在20 kvar和0 kvar上下波动；燃料电池和光伏电池组无功输出平稳，燃料电池输出的无功功率在15 kvar左右波动，光伏电池无功输出恒为0 kvar。多微电网母线电压在（1±0.005）p.u.左右波动，系统频率在（50±0.02）Hz左右小范围波动，满足系统最低要求。

在第5 s时，将子微电网A与大电网母线相连的开关BRK1断开，从图11可知微型燃气轮机和光伏电池组的无功输出功率恒不变，燃料电池和风力发电机组的无功输出功率分别一直在15 kvar和0 kvar小范围波动。而从图12、13可知母线电压和系统频率也恒不变。

由以上分析可知，在子微电网A中的微型燃气轮机和光伏电池组发生故障时，子微电网B中的燃料电池起到了良好的调节作用，使母线电压和系统频率十分平稳。

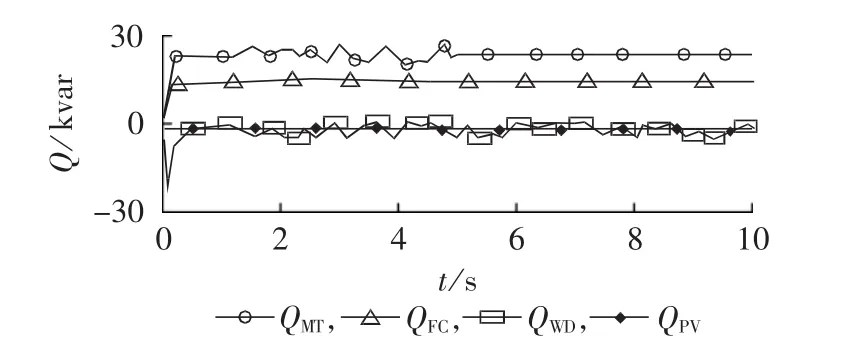
图11 燃气轮机和光伏电池组故障时各微源元胞输出无功功率Fig.11 Output reactive powers of micro-source cellular when gas turbine and photovoltaic cells fail

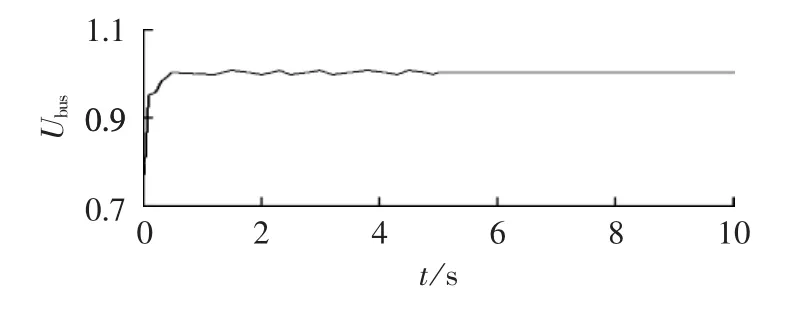
图12 燃气轮机和光伏电池组故障时母线电压有效值Fig.12 Effective value of bus voltage when gas turbine and photovoltaic cells fail

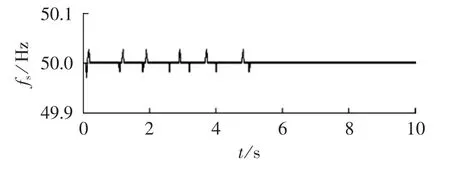
图13 燃气轮机和光伏电池组故障时系统频率Fig.13 System frequency when gas turbine and photovoltaic cells fail

4.2.4 燃料电池和风力发电机（子微电网B）故障对多微电网的影响

开始时，各子微电网在孤网模式下各自平稳运行，在第5 s时将子微电网B与母线连接的开关BRK2断开，来模拟燃料电池和风力发电机故障，仿真时间为10 s，仿真结果如图14—16所示。

由图14可知，在0～5 s，微型燃气轮机和风力发电机波动较大，且其无功输出分别在20 kvar和0 kvar上下波动。燃料电池和光伏电池组无功输出平稳，燃料电池输出的无功功率在15 kvar左右波动，光伏电池无功输出恒为0kvar。多微电网母线电压在（1±0.005）p.u.左右波动，系统频率在（50±0.02）Hz左右小范围波动，满足系统最低要求。

在第5 s时，将子微电网B与大电网母线相连的开关BRK2断开，从图14可知燃料电池和风力发电机组的无功输出功率恒不变，微型燃气轮机和光伏电池组的无功输出功率分别一直在20 kvar和0 kvar左右波动。而从图15、16可知母线电压和系统频率也恒不变。

由以上分析可知，在微型燃气轮机和光伏电池组发生故障时，微型燃气轮机起到了良好的调节作用，各子微电网之间相互协调交互的效果明显，使母线电压和系统频率十分平稳。

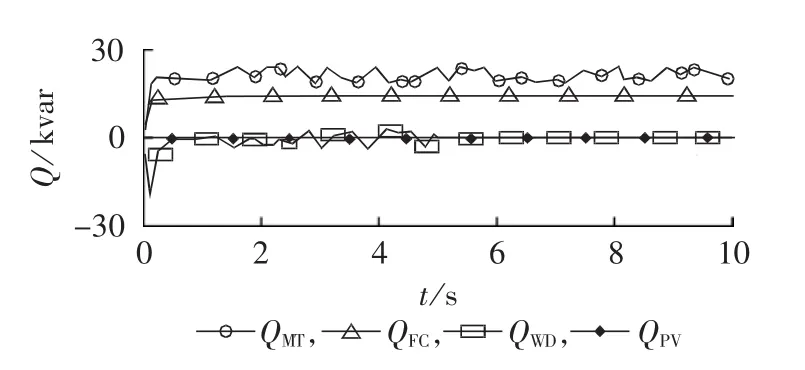
图14 燃料电池和风力发电机故障时各微源元胞输出无功功率Fig.14 Output reactive powers of micro-source cellular when fuel cells and wind turbine fail

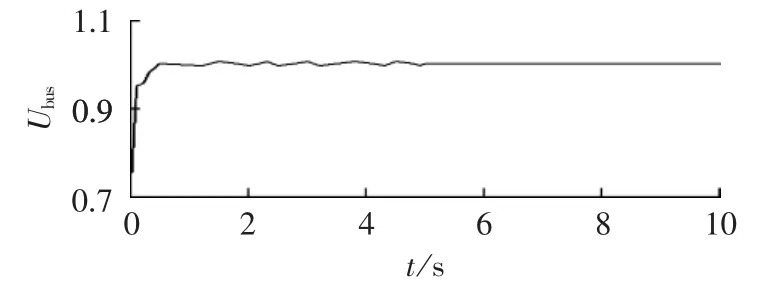
图15 燃料电池和风力发电机故障时母线电压有效值Fig.15 Effective value of bus voltage when fuel cells and wind turbine fail

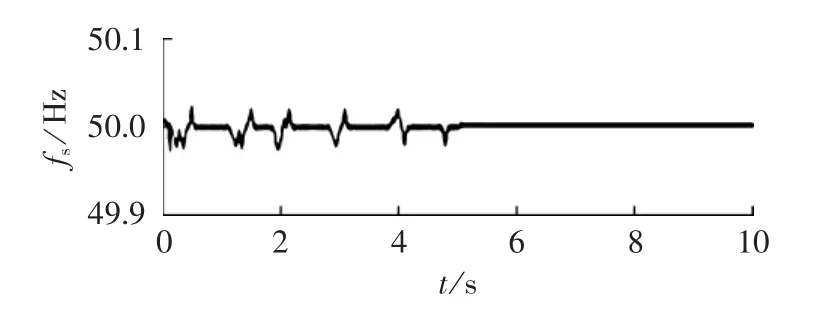
图16 燃料电池和风力发电机组故障时系统频率Fig.16 System frequency when fuel cells and wind turbine fail

4.3 和其他无功电压控制方法的比较

通过上面的实验以及分析可以得知，在孤岛模式下使用MAS与CA的双层多微电网无功电压控制模型可以很好地调节和控制微电网的母线电压及微电源的无功输出功率。上文提到，MAS和下垂控制法是目前电压控制领域中比较常用的电力电子技术方法，而基于MAS和CA的无功电压控制方法较之于其他微电网无功电压控制的优势主要体现在以下几个方面。

a.下垂控制法没有考虑到系统电压的恢复问题，因此当微电网遭受严重干扰时，系统的电压质量可能无法保证；单一的MAS控制虽然可以在一定程度上对微源元胞进行调压，但它不能检测各个子微电网微源元胞的运行状态，不能及时地做出响应；而本文提出的基于MAS和CA的电压控制法不仅可以对微源元胞进行实时监控，还可以向MAS反映元胞的状态，使其快速地给出解决方法，并且通过实现电压控制策略可以达到恢复系统电压的目的，即使在微电网遭受严重扰动时，仍然能够保证整个微电网电压的质量。

b.下垂控制法仅针对各分布式电源间的控制，MAS以及CA方法适用于微电网模型中的任何元器件，元件可灵活地加入微电网中，并对其进行实时监测。

c.下垂控制法没有考虑微源之间、负荷之间以及微源与负荷之间、微电网主控单元与微源和负荷之间的协调问题，调节电压相对主观；而MAS技术考虑到了这一点，提供了通信机制，可以令各元器件之间协调调压；而本文加入的CA可以和MAS进行实时通信，使多微电网的无功电压控制方法更加有效，这在本文实验中已有所体现。文献［23］将下垂控制法在微电网模型上进行了仿真，从仿真结果来看，虽然该方法也能够达到调整无功输出、稳定系统电压的目的，但相比本文提出的方法，下垂控制法在时间上不具有优势；文献［7］将MAS方法应用于孤岛模式下电力系统的无功电压的控制中，从该文实验结果可以看出，微电网从扰动恢复稳态的时间较本文提出的MAS和CA控制方法的电压控制在时间上（见图5）有所逊色。三者的微电网无功电压控制时间比较如表3所示。其中，t1为微电网从启动到状态稳定的时间；t2为系统从并网模式切换到孤岛模式后恢复到稳定状态的时间。

表3 各种方法在时间上的比较Table 3 Comparison of time consumption among different control methods

5 结论

本文建立了基于MAS和CA的双层多微电网孤岛模式下无功电压控制模型。该模型包括上下两层结构，上层模型通过系统中的各Agent之间的交互信息来实现微电网分布式协调控制功能；下层模型基于CA建模，用来描述微电网中微源和负荷的参数变化情况，为系统中Agent的决策提供所需信息。通过该模型提出了MAS和CA相结合的多微电网无功电压的分布式协调控制策略，最后通过仿真实验证明了该策略对孤岛模式下的多微电网的无功电压输出、系统频率和母线电压具有良好的控制效果。基于MAS和CA的多微电网无功电压控制具有较高的灵活性和智能性，在微电网的控制方面中取得了一定的进步。

本文对多微电网孤岛模式下的无功电压控制构建了分布式控制模型，提出了分布式控制策略，但是并未考虑多微电网的有功功率变化以及多微电网在并网模式下的母线电压以及系统频率的控制，这些问题需进一步研究。

［1］张建华，黄伟.微电网运行控制与保护技术［M］.北京：中国电力出版社，2010：7.

［2］季阳，艾芊，解大.分布式发电技术与智能电网技术的协同发展趋势［J］.电网技术，2010，34（12）：15-23.JI Yang，AI Qian，XIE Da.Research on co-developmental trend ofdistributed generation and smartgrid［J］.PowerSystem Technology，2010，34（12）：15-23.

［3］BASU A K.Microgrids：energy management by strategic deployment of DERs-a comprehensive survey［J］.Renewable and Sustainable Energy Reviews，2011，15（9）：4348-4356.

［4］王成山，王守相.分布式发电供能系统若干问题研究［J］.电力系统自动化，2008，32（20）：1-4，31.WANG Chengshan，WANG Shouxiang.Study on some key problems related to distributed generation systems［J］.Automation of Electric Power Systems，2008，32（20）：1-4，31.

［5］IRAVANI R，HATZIARGYRIOU N，DIMEAS A，et al.Micro-grids management［J］.IEEE Power and Energy Magazine，2008，6（3）：54-65.

［6］REN Hongbo，ZHOU Weisheng，NAKAGAMIK，etal.Multiobjective optimization for the operation ofdistributed energy systems considering economic and environmentalaspects［J］.Applied Energy，2010，87（12）：3642-3651.

［7］鲁斌，衣楠.孤岛模式下微电网自趋优分布式无功电压控制策略［J］.电力系统自动化，2014，38（9）：218-225.LU Bin，YI Nan.A self-approximate-optimal distributed reactive power and voltage control strategy for microgrid in island mode［J］.Automation of Electric Power Systems，2014，38（9）：218-225.

［8］李鹏，窦鹏冲，李雨薇，等.微电网技术在主动配电网中的应用［J］. 电力自动化设备，2015，35（4）：8-16.LI Peng，DOU Pengchong，LI Yuwei，et al.Application of microgrid technology in active distribution network［J］.Electric Power Automation Equipment，2015，35（4）：8-16.

［9］赵卓立，杨革，蔡泽祥，等.含风电孤立中压微电网暂态电压稳定协同控制策略［J］. 电力自动化设备，2015，35（10）：1-9.ZHAO Zhuoli，YANG Ge，CAI Zexiang，et al.Cooperative control of transient voltage stability for islanded medium-voltage microgrid with wind power［J］.Electric PowerAutomation Equipment，2015，35（10）：1-9.

［10］丁磊.多微网配电系统的分层孤岛运行及保护控制［D］.济南：山东大学，2007.DING Lei.Multi-tiered island operation and protection of micro grid distribution system control［D］.Ji’nan：Shandong University，2007.

［11］杨青生，黎夏.多智能体与元胞自动机结合及城市用地扩张模型［J］. 地理科学，2007，27（4）：542-548.YANG Qingsheng，LI Xia.Integration of multi-agent systems with cellular automata for simulating urban land expansion［J］.Geographical Sciences，2007，27（4）：542-548.

［12］王砚帛，谭永东，文菓，等.基于Fisher判别和元胞自动机模型的微电网格局计算方法［J］.电网技术，2012，36（11）：12-17.WANG Yanbo，TAN Yongdong，WEN Guo，et al.An approach to calculate micro-grid’s configuration based on Fisher discriminant and cellular automata model［J］.Power System Technology，2012，36（11）：12-17.

［13］杨丽徒，王金凤，陈根永，等.基于元胞自动机理论的电力负荷空间分布预测［J］. 中国电机工程学报，2007，27（4）：15-20.YANG Lixi，WANG Jinfeng，CHEN Genyong，et al.Load spatial distribution forecasting model on cellular automata theory［J］.Proceedings of the CSEE，2007，27（4）：15-20.

［14］刘小平，黎夏.Fisher判别及自动获取元胞自动机的转换规则［J］.测绘学报，2007，36（1）：112-117.LIU Xiaoping，LI Xia.Fisher discriminant and automatically getting transition rule ofCA［J］.JournalofSurveying and Mapping，2007，36（1）：112-117.

［15］衣楠.微网分布式协调控制系统设计及仿真实现［D］.保定：华北电力大学，2014.YI Nan.Design and simulation of microgrid distributed coordination control system［D］.Baoding：North China Electric Power University，2014.

［16］GUERRERO JM，VICUNA L G，MATASJ，etal.Output impedance design ofparallel-connected UPS inverterswith wireless load-sharing control［J］.IEEE Transactions on Industrial Electronics，2005，52（40）：1126-1135.

［17］LI Yan，LI Yunwei.Decoupled power control for an inverter based low voltage microgrid in autonomous operation［C］∥IEEE 6th International Power Electronics and Motion Control Conference.Wuhan，China：IEEE，2009：2490-2496.

［18］吴雄，王秀丽，刘世民，等.微电网能量管理系统研究综述［J］.电力自动化设备，2014，34（10）：7-14.WU Xiong，WANG Xiuli，LIU Shimin，et al.Summary of microgrid energy management system［J］.Electric Power Automation Equipment，2014，34（10）：7-14.

［19］范玉顺，曹军威.多代理系统理论、方法与应用［M］.北京：清华大学出版社，2002：1-4.

［20］刘春阳，王秀丽，刘世民，等.计及蓄电池使用寿命的微电网经济调度模型［J］. 电力自动化设备，2015，35（10）：29-36.LIU Chunyang，WANG Xiuli，LIU Shimin，etal.Themicroeconomic dispatch model and battery life meter［J］.Electric Power Automation Equipment，2015，35（10）：29-36.

［21］MARIJA D I，LIU Xiaojun，GILBERT L.Improved secondary and new tertiary voltage control［J］.IEEE Transactions on Power Systems，1995，10（4）：1851-1862.

［22］余涛，周斌.基于强化学习的互联电网CPS自校正控制［J］.电力系统保护与控制，2009，37（10）：33-38.YU Tao，ZHOU Bin.Reinforcement learning based CPS selftuning control methodology for interconnected power systems［J］.Power System Protection and Control，2009，37（10）：33-38.

［23］刘静，陶晓峰.基于下垂特性的分布式发电系统的设计［J］.电子测量与仪器学报，2011，25（7）：635-641.LIU Jing，TAO Xiaofeng.Design of distributed generation system based on droop characteristric［J］.Journal of Electronic Measurement and Instrument，2011，25（7）：635-641.