应用于交流微电网谐振抑制的有源阻尼器及控制
曾 正,徐盛友,冉 立,陈民铀
(重庆大学 输配电装备及系统安全与新技术国家重点实验室,重庆 400044)
0 引言
微电网作为传统大电网的重要补充,在可再生能源接入、海岛等边远地区供电、提高供电可靠性等方面具有重要的意义,近来得到了广泛的理论研究和工程示范[1-3]。微电网内的可再生能源大多需要通过并网逆变器接入电网[4-5],单台并网逆变器的运行和控制得到了深入的研究[6-7],尤其是单台并网逆变器因LCL滤波器引发的谐振问题也得到了很好的解决[8-9]。但是,由于微电网内往往含有大量的并网逆变器、线路和各种复杂负荷,近年来,在众多的微电网示范工程中相继出现了严重的谐波谐振现象,以及由此引发的逆变器无故障跳闸事故[10-11],给微电网的安全稳定运行带来了不小的挑战。
针对微电网谐波谐振的机理及其应对,已有部分研究成果。文献[12-15]从并网逆变器的开环模型出发,建立了包含并网逆变器、负荷和线路阻抗的微电网电路模型,从电路的角度分析了微电网中谐波谐振的机理。文献[16-17]考虑了并网逆变器的控制策略对其运行特性的影响,从闭环模型的角度分析了含有多台并网逆变器的微电网中谐波谐振的机理,并提出了一种虚拟阻抗的控制策略来抑制谐振的发生。文献[18-20]提出重塑并网逆变器的输出阻抗,向微电网提供更多的串联或并联虚拟电阻,可有效地抑制微电网中的谐波谐振。但是,这些方法大多要求重新升级并网逆变器的控制程序,在并网逆变器中引入虚拟电阻,这在实际应用中往往存在一定的局限性。首先,微电网中的并网逆变器大多是不同类型、不同容量和不同厂家的产品,在并网逆变器控制程序的通用性、程序的升级改造方面还有待进一步的研究[21];其次,这些并网逆变器在被重新塑造输出阻抗后,相互间的协调控制也有待进一步的研究;再次,虚拟阻抗控制会影响到并网逆变器的输出特性,尤其是可能改变并网逆变器的输出电流波形,影响并网电流的电能质量;最后,让并网逆变器参与微电网谐波谐振的抑制,会改变逆变器的工作模式,并可能影响到并网逆变器的正常使用寿命[22]。因此,利用微电网中的并网逆变器治理其中的谐波谐振还有待进一步的深入研究。相反,为了应对多变流器系统中的谐波谐振,文献[23]提出了有源阻尼器AD(Active Damper)的概念,在含有多台PWM整流器的系统中,通过额外引入的电力电子装置来抑制可能出现的谐波谐振。但是,该有源阻尼器需要检测系统的谐振频率,仅针对特定次的谐波谐振进行治理,而微电网中的谐波谐振往往较复杂且是时变的,难以存在固定的谐振频率。
本文提出一种有源阻尼器控制策略来有效地治理微电网中的谐波谐振,通过有源阻尼器向微电网谐波网络注入虚拟的电阻和电导,提高微电网对谐波谐振的抑制能力。在建立有源阻尼器数学模型和控制策略的基础上,结合一个微电网算例,利用PSCAD/EMTDC的仿真结果验证了所提有源阻尼器及其控制策略的正确性和有效性,为微电网谐波谐振的抑制提供了一条新的有效途径。
1 有源阻尼器的模型与控制
图1给出了一个含有源阻尼器、2台逆变器型分布式发电机DG(Distributed Generator)和 2组局部负荷的典型微电网结构。其中,有源阻尼器是一种小容量的电力电子装置,类似于传统的有源滤波器,它可以向微电网注入特定谐振频率的谐波电流,消除微电网中的谐波谐振。但是,它又不同于有源滤波器:一方面,由于有源阻尼器只需要针对微电网高次谐波谐振频率处的电压和电流分量加以治理,因此所需的容量较有源滤波器会小很多,这是它和传统并联型有源滤波器或阻性有源滤波器[24-25]之间的本质区别;另一方面,它仅需检查其并网点处的电压和电气下游电流,并进行控制,不需要像传统有源滤波器那样采样其并联点处的负荷电流信息。总之,相比于传统有源滤波器,在微电网中只需安装一个容量不大的有源阻尼器即可有效治理微电网中宽频段范围内的谐波谐振。
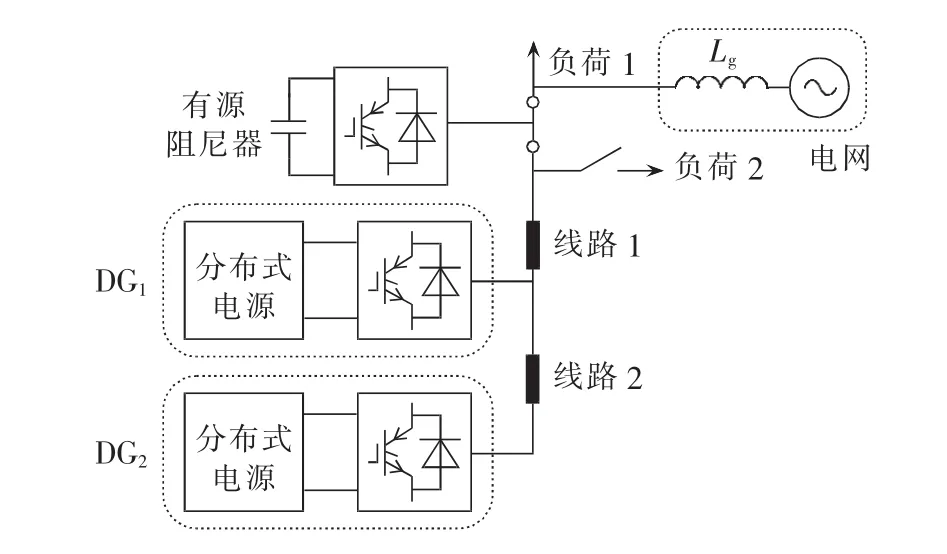
图1 一个包含有源阻尼器的微电网Fig.1 A microgrid with AD
下面给出有源阻尼器的电路结构和控制策略,如图2所示。有源阻尼器和DG均采用三相两电平电路和LCL滤波器结构,其中L1和L2分别为逆变器侧和网侧滤波电感,Rd为阻尼电阻,C为滤波电容,Kpwm=Udc/2为逆变器的等效放大系数。控制器中,采用恒功率Park变换:

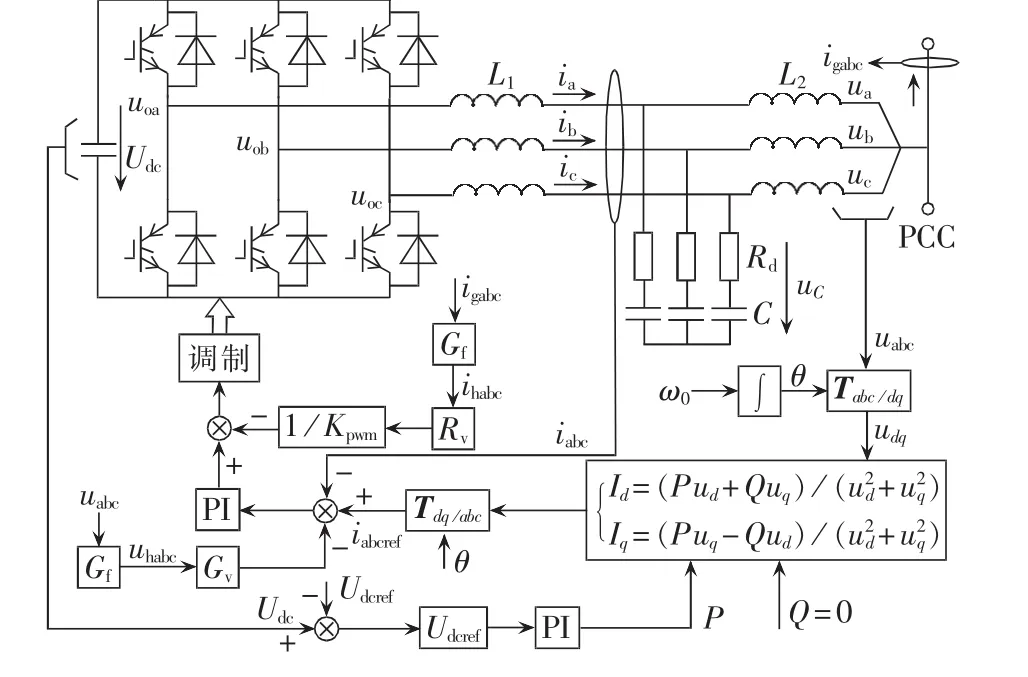
图2 有源阻尼器的控制策略Fig.2 Control scheme of AD
其逆变换满足这里采用无锁相环的电网同步技术[26],相位θ由电网额定角频率 ω0=2πf0积分产生,即有功指令 P 用于维持直流母线电压为恒定的Udcref,通过对直流母线电压的反馈控制得到;无功指令Q设置为0。在得到dq轴下的电网电压分量udq后,进而获得电流指令Idq[26],经反Park变换后可得输出功率部分的指令电流在abc坐标系下的结果iabcref,再经电流跟踪控制器和调制策略得到逆变器所需的开关脉冲。
如图2所示,为了使有源阻尼器获得虚拟电阻输出的能力,以抑制微电网中可能出现的谐波谐振,有源阻尼器检测机端公共耦合点(PCC)处的电流igabc,经过陷波器Gf(s)滤除基波电流后得到谐波电流ihabc,再引入虚拟电阻Rv后,加入PI控制器的输出,考虑到逆变电路的放大作用,这里需要乘以系数1/Kpwm。其中,陷波器的数学模型为:

其中,k影响陷波器的响应速度和带宽,通常,参数k 优化地选为 1.414[18,27]。类似地,电网电压 uabc经过陷波器滤除基波分量后引入虚拟电导Gv,然后加入有源阻尼器的输出电流指令中。
图3给出了包含有源阻尼器时微电网的等效电路模型,其中Z1和Z2分别为DG1和DG2的输出阻抗,ZL为负荷的等效阻抗,i1和i2分别为其输出并网电流相量,u1、u3、uh分别为电网电压基波、3 次谐波和h次谐波相量。为了分析谐波特性,由电路的叠加原理,可去除基波分量的电路网络。此外,假设虚拟的电阻和电导远大于线路和逆变器的输出阻抗,图3(a)中电路网络可以简化为如图 3(b)所示的谐波域中的微电网等效电路模型,其中∑i1h和∑i2h分别为DG1和DG2的并网谐波电流之和。那么,逆变器的输出谐波电流和电网谐波电压对于PCC处的并网电流的传递函数可以表示为:
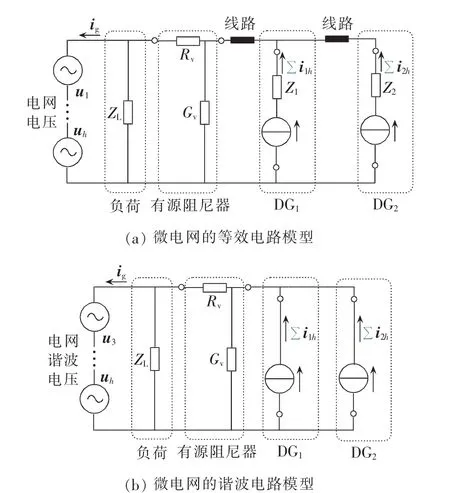
图3 含有源阻尼器微电网的谐波网络模型Fig.3 Harmonic network model of microgrid with AD
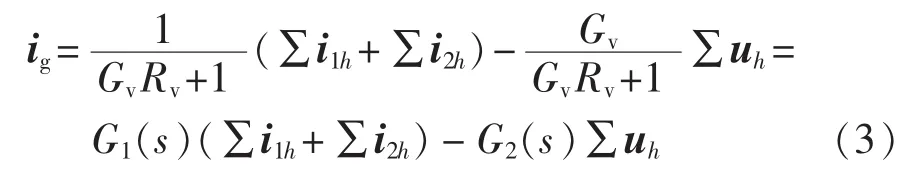
其中,G1为微电网网络中DG输出谐波电流对PCC处谐波电流的增益,而G2则反映了电网谐波电压对PCC处谐波电流的增益。图4给出了不同虚拟电阻和虚拟电导对G1和G2增益的影响。
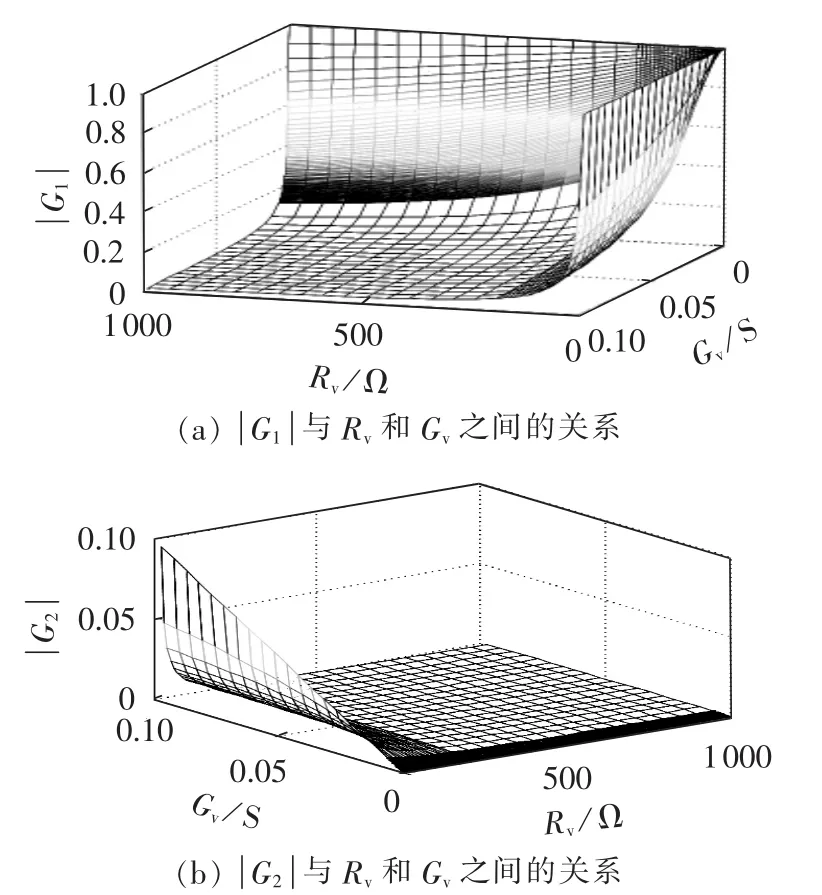
图4 AD虚拟电阻和电导对谐波电流和电压的衰减性能Fig.4 Performance of AD introducing virtual resistance and conductance to damp harmonic voltage and current
由式(3)可知,Rv和 Gv之间存在耦合,DG 的谐波电流到PCC处并网电流之间的传递函数G1的增益由Rv和Gv的乘积决定,其关系如图5所示。RvGv越大,虚拟电阻和电导对谐波电流的衰减能力越强。相反,若RvGv=0,即在没有虚拟电阻或虚拟电导时,并网逆变器输出电流所激发的谐波谐振电流可以无衰减地注入电网。这是因为,一方面,当Rv=0时,图3(b)所示谐波电压对于电流源短路,Gv的阻尼效果被短接,谐波电流可以自由地注入电网;另一方面,当Gv=0时,图3(b)所示虚拟电导支路开路,逆变器输出的谐波电流也可以自由地注入电网。
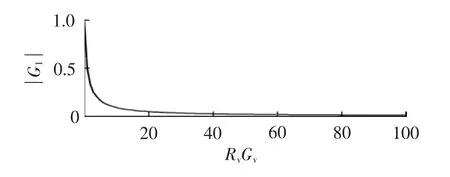
图5 逆变器电流的放大系数Fig.5 Gain of inverter current
2 仿真结果与分析
为了验证前述有源阻尼器在微电网谐波谐振抑制中的正确性和有效性,在PSCAD/EMTDC中建立了如图1所示的微电网系统模型。有源阻尼器参数:LCL滤波器 L1=1mH、L2=0.5mH、C=20μF、Rd=4Ω;直流母线电压Udcref=700V;直流电压PI环Kp=0.8、Ti=0.01 s;交流电流 PI环 Kp=0.6、Ti=0.01 s;开关频率fs=10kHz。电网参数:电感Lg=3mH;线电压有效值380V;额定频率f0=50Hz。线路参数:线路1和2的长度分别为0.1km、0.2km;单位长度的线路电阻r0=0.642Ω /km、感抗 x0=0.083Ω /km。DG 参数:LCL滤波器 L1=1mH、L2=0.6mH、C=20μF、Rd=4 Ω;直流母线电压Udcref=700 V;开关频率fs=10 kHz。负荷参数:负荷1电阻25Ω;负荷2电阻40Ω。
DG的控制系统框图如图6所示,其中PLL为锁相环,P和Q分别为有功和无功功率指令,DG1和DG2的功率指令分别为 6kW /0var、8kW /0var。仿真过程中,0.1s时切除40 Ω的电阻负荷2,降低负荷阻抗对系统谐振的阻尼。为了便于比较有源阻尼器的控制效果,0.2s前有源阻尼器仅对直流母线充电,将电压稳定在给定值Udcref,此时Rv=0Ω、Gv=0S;0.2 s开始投入虚拟电阻和电导控制,此时Rv=475Ω、Gv=0.04S。
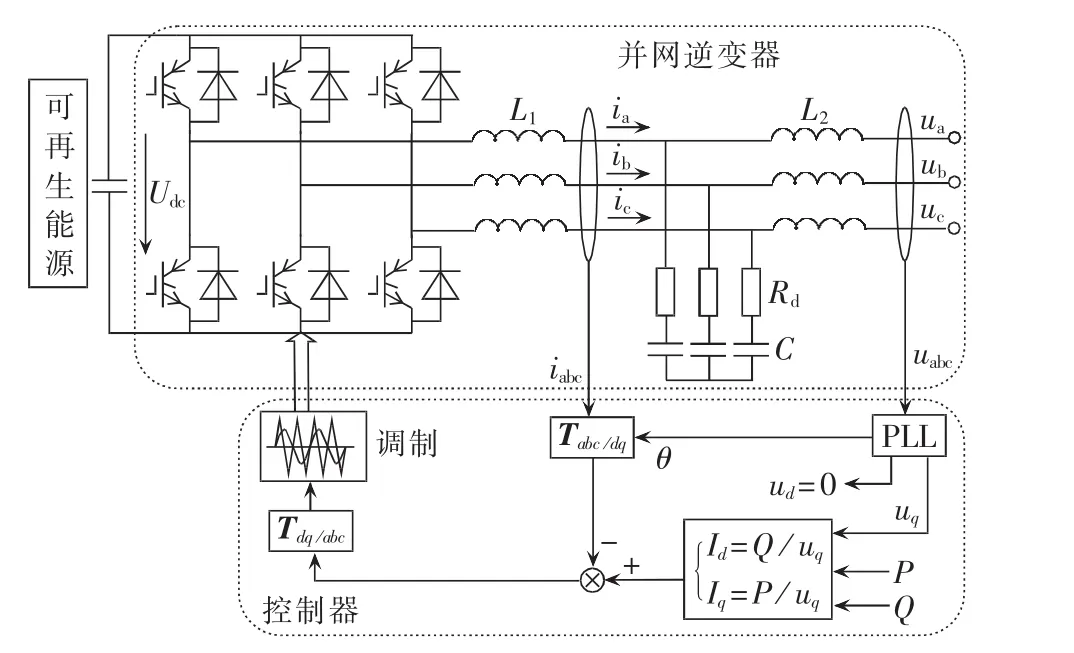
图6 DG的控制框图Fig.6 Block diagram of DG control
图7给出DG1和DG2的输出电流波形及其THD分布。可以发现,当负荷切除后(0.1~0.2s),网络内负荷降低,并联电阻变大,降低了对谐波电流的抑制能力。在0.1 s切除负荷这一扰动激发了网络内的谐波谐振,DG1和DG2的输出电流波形中产生了大量的谐波,其THD远远超出了IEEE或我国的相关标准的要求。有源阻尼器在0.2 s投入谐振阻尼控制后,微电网内的谐波谐振得到了有效抑制,2台DG的输出电流波形更接近正弦,THD大幅降低。
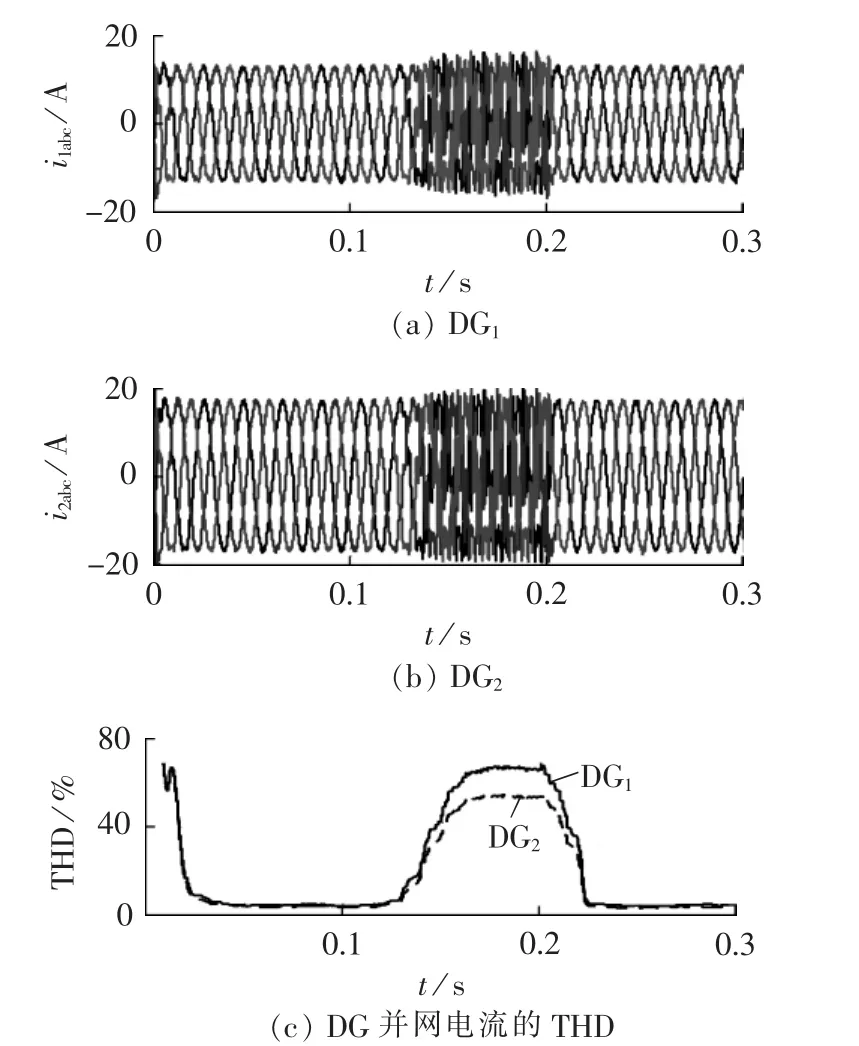
图7 DG1和DG2的输出电流Fig.7 Output current of DG1and DG2
图8给出了PCC处电网电压的波形及其THD。从中可以发现,在有源阻尼器不投入谐振抑制功能时,微电网内多变流器间形成了谐波谐振,同时,谐波电流在网络阻抗上产生谐波电压,使得PCC处的电压也出现了严重的畸变。

图8 PCC处电压及其谐波Fig.8 Voltage at PCC and its THD
图9给出了微电网注入配电网的电流的瞬时波形,正如前面分析的那样,在有源阻尼器谐振阻尼功能激活前,网络内的谐振使得微电网的入网电流畸变增大,同时并网功率也相应地出现了谐振。谐振抑制功能激活后,能有效改善入网电流的电能质量,降低了微电网对配电网的冲击和不利影响。
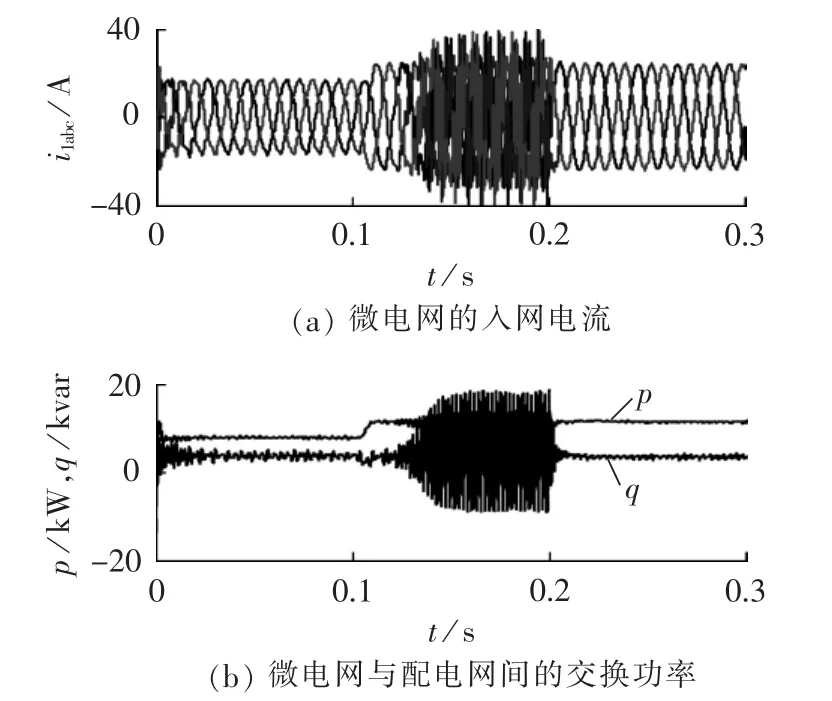
图9 PCC并网电流及其功率Fig.9 Grid-connecting current and power at PCC
图10给出了有源阻尼器的启动过程,即直流母线电压的充电过程。可见,在有源阻尼器开机后,有源阻尼器类似于PWM整流器运行,向直流母线充电,使得直流母线电压稳定在700V。当其参与微电网谐波谐振抑制时,除了小的动态过程外,直流母线电压能较好地稳定在预期的700V。
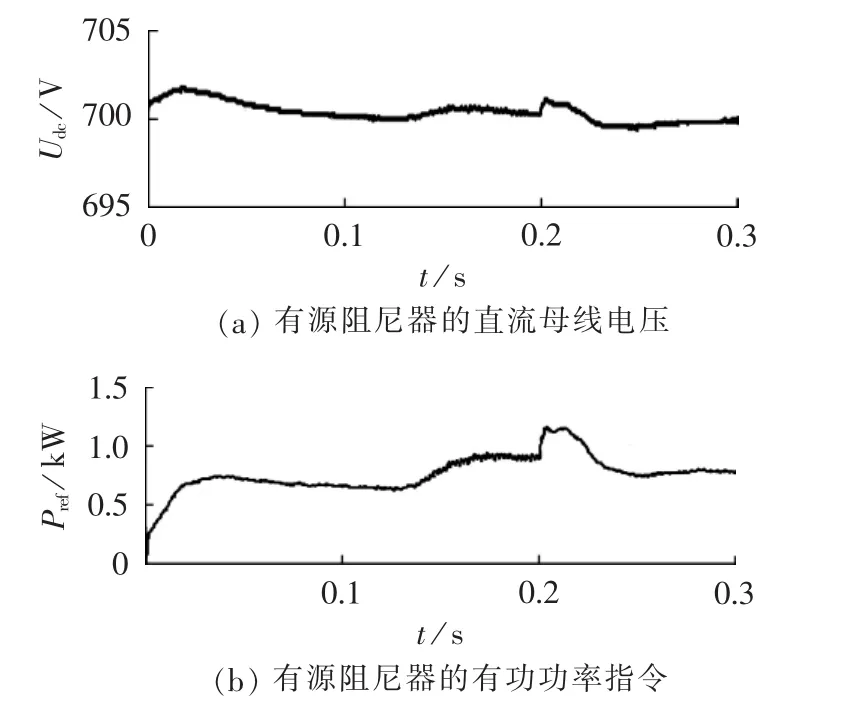
图10 有源阻尼器的直流母线电压和功率Fig.10 DC-link voltage and active power of AD
图11给出了有源阻尼器所检测到的a相并网点电压和有源阻尼器输出电流的谐波分量。可见,所提的陷波器能很好地从有源阻尼器并网点电压和电流中检测出其谐波电压和谐波电流,以便用于虚拟电阻和电导控制。
图12给出了有源阻尼器的输出电流,在开机时,由于给直流母线电压充电,使得其并网电流中主要为工频基波电流分量,直流母线电压稳定到额定值之后,有源阻尼器的并网电流基本上没有了基波有功分量,其基波分量主要由滤波电容支路的无功电流引起。相反,有源阻尼器的输出电流主要为谐波分量,这些谐波电流分量主要是为了抑制网络内的谐波电压和谐波电流而产生的补偿分量。在0.1~0.2 s之间,微电网内所激发出的谐波谐振使得PCC电压畸变,并影响到了有源阻尼器指令电流的计算和跟踪,使得有源阻尼器的输出电流波形也出现了严重的畸变。
综上,可以发现,所提出的有源阻尼器及其控制策略,可以在不改变并网逆变器及其控制策略的基础上,通过额外安装一个小容量的变流器装置,向微电网提供必要的虚拟电阻和虚拟电导,有效地抑制微电网内可能出现的谐波谐振。
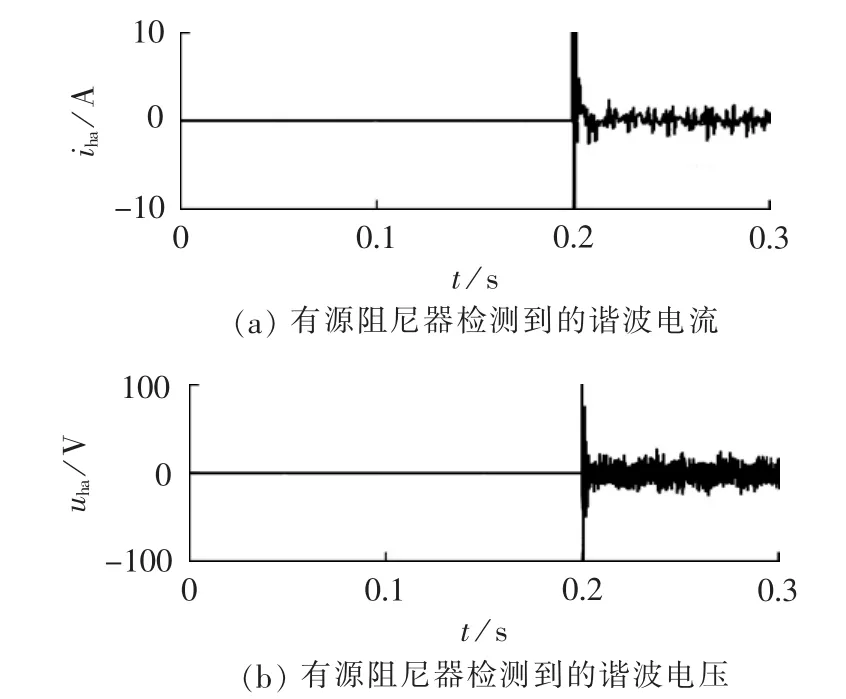
图11 有源阻尼器检测到的谐波电流和谐波电压Fig.11 Harmonic voltage and current detected by AD
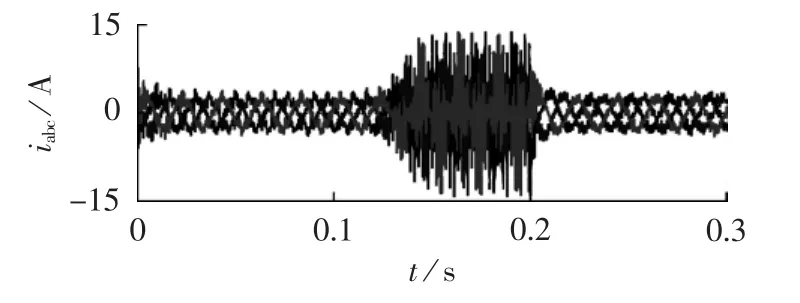
图12 有源阻尼器的输出电流Fig.12 Output current of AD
3 结论
本文针对微电网的谐波谐振进行了研究,提出了一种有源阻尼器及其控制方案,能有效地抑制微电网中的谐波谐振,并利用仿真结果进行了验证,可以得出以下结论:
a.微电网中变流器的滤波网络、负荷和线路之间通过阻抗耦合在一起,可能形成复杂的谐波网络,负荷电阻对于谐波谐振的抑制具有一定的益处,负荷越重则对谐波谐振的抑制能力越强;
b.陷波器能有效地从有源阻尼器检测并网点处的谐波电压和谐波电流,并向微电网注入给定虚拟的电阻和电导,增加微电网抑制谐波谐振的能力;
c.由于只需额外安装容量很小的有源阻尼器,无需改变并网逆变器的硬件或软件,为微电网中谐波谐振抑制提供了一条新的有效方案。
[1]王成山,李鹏.分布式发电、微网与智能配电网的发展与挑战[J].电力系统自动化,2010,34(2):10-14.WANG Chengshan,LIPeng.Developmentand challengesof distributed generation,the micro-grid and smart distribution system[J].Automation of Electric Power Systems,2010,34(2):10-14.
[2]程军照,李澍森,冯宇,等.发达国家微网政策及其对中国的借鉴意义[J]. 电力系统自动化,2010,34(1):64-68.CHENG Junzhao,LI Shusen,FENG Yu,et al.Policies on microgrid in developed countries and implications for China[J].Automation of Electric Power Systems,2010,34(1):64-68.
[3]ZENG Z,ZHAO R,YANG H,et al.Policies and demonstrations of micro-grids in China:a review[J].Renewable and Sustainable Energy Reviews,2014,29:701-718.
[4]BLAABJERG F,CHEN Z,KJAER S B.Power electronics as efficientinterface in dispersed powergeneration systems [J].IEEE Transactions on Power Electronics,2004,19(5):1184-1194.
[5]曾正,赵荣祥,汤胜清,等.可再生能源分散接入用先进并网逆变器研究综述[J]. 中国电机工程学报,2013,33(24):1-12.ZENG Zheng,ZHAO Rongxiang,TANG Shengqing,etal.An overview on advanced grid-connected inverters used for decentralized renewable energy resources[J].Proceedings of the CSEE,2013,33(24):1-12.
[6]ROCABERT J,LUNA A,BLAABJERG F,et al.Control of power converters in AC microgrids[J].IEEE Transactions on Power Electronics,2012,27(11):4734-4749.
[7]CARRASCO J M,FRANQUELO L G,BIALASIEWICZ J T,et al.Power-electronic systems for the grid integration of renewable energy sources:a survey[J].IEEE Transactionson Industrial Electronics,2006,53(4):1002-1016.
[8]谢少军,许津铭.LCL滤波并网逆变器的电流控制技术研究综述[J]. 电源学报,2012(4):1-6,18.XIE Shaojun,XU Jinming.Overview of current control strategy for grid-tied inverters with LCL filters[J].Journal of Power Supply,2012(4):1-6,18.
[9]肖华锋,许津铭,谢少军.LCL型进网滤波器的有源阻尼技术分析与比较[J]. 电力自动化设备,2013,33(5):55-59.XIAO Huafeng,XU Jinming,XIE Shaojun. Analysis and comparison of active damping technologies for LCL filter[J].Electric Power Automation Equipment,2013,33(5):55-59.
[10]ENSLIN J H R,HESKES P J M.Harmonic interaction between a large number of distributed power inverters and the distribution network[J].IEEE Transactions on Power Electronics,2004,19(6):1586-1593.
[11]周林,张密.大型光伏电站谐振现象分析[J].电力自动化设备,2014,34(6):8-14.ZHOU Lin,ZHANG Mi.Analysis of resonance phenomenon in large-scale photovoltaic power plant[J].Electric Power Automation Equipment,2014,34(6):8-14.
[12]AGORRETA J L,BORREGA M,LO X,et al.Modeling and control of N-paralleled grid-connected inverters with LCL filter coupled due to grid impedance in PV plants[J].IEEE Transactions on Power Electronics,2011,26(3):770-785.
[13]谢宁,罗安,马伏军,等.大型光伏电站与电网谐波交互影响[J].中国电机工程学报,2013,33(34):9-16.XIE Ning,LUO An,MA Fujun,etal.Harmonic interaction between large-scale photovoltaic power stations and grid[J].Proceedings of the CSEE,2013,33(34):9-16.
[14]胡伟,孙建军,马谦,等.多逆变器并网系统谐振特性分析[J].电力自动化设备,2014,34(7):93-98.HU Wei,SUN Jianjun,MA Qian,et al.Resonant characteristics of multi-inverter grid-connection system[J].Electric Power Automation Equipment,2014,34(7):93-98.
[15]许德志,汪飞,毛华龙,等.多并网逆变器与电网的谐波交互建模与分析[J]. 中国电机工程学报,2013,33(12):64-71.XU Dezhi,WANG Fei,MAO Hualong,etal.Modelingand analysis of harmonic interaction between multiple gridconnected inverters and the utility grid[J].Proceedings of the CSEE,2013,33(12):64-71.
[16]HE J,LI Y W,BOSNJAK D,et al.Investigation and active damping ofmultiple resonancesin a parallel-inverter-based microgrid[J].IEEE Transactions on Power Electronics,2013,28(1):234-246.
[17]周林,张密,居秀丽,等.电网阻抗对大型并网光伏系统稳定性影响分析[J]. 中国电机工程学报,2013,33(34):34-41.ZHOU Lin,ZHANG Mi,JU Xiuli,et al.Stability analysis of large-scale photovoltaic plants due to grid impedances[J].Proceedings of the CSEE,2013,33(34):34-41.
[18]曾正,赵荣祥,吕志鹏,等.光伏并网逆变器的阻抗重塑与谐波谐振抑制[J]. 中国电机工程学报,2014,34(27):4547-4558.ZENG Zheng,ZHAO Rongxiang,LÜ Zhipeng,et al.Impedance reshaping of grid-tied inverters to damp the series and parallel harmonic resonances of photovoltaic systems[J].Proceedings of the CSEE,2014,34(27):4547-4558.
[19]SUN J.Impedance-based stability criterion for grid-connected inverters[J].IEEE Transactions on Power Electronics,2011,26(11):3075-3078.
[20]YANG D,RUAN X,WU H.Impedance shaping of the gridconnected inverter with LCL filter to improve its adaptability to the weak grid condition[J].IEEE Transactions on Power Electronics,2014,29(11):5795-5805.
[21]曾正.多功能并网逆变器及其微电网应用[D].杭州:浙江大学,2014.ZENG Zheng. Multi-functional grid-connected inverter for microgrid application[D].Hangzhou:Zhejiang University,2014.
[22]YANG S,XIANG D,BRYANT A,et al.Condition monitoring for device reliability in power electronic converters:a review [J].IEEE Transactions on Power Electronics,2010,25 (11):2734-2752.
[23]WANG X,BLAABJERG F,LISERRE M,et al.An active damper for stabilizing power-electronics-based AC systems[J].IEEE Transactions on Power Electronics,2014,29(7):3318-3329.
[24]PRODANOVIC M,de BRABANDERE K,van den KEYBUS J,et al.Harmonic and reactive power compensation as ancillary services in inverter-based distributed generation[J].IET Generation,Transmission&Distribution,2007,1(3):432-438.
[25]孙孝峰,曾健,张芳,等.阻性有源滤波器分频控制位置的选择方案[J]. 中国电机工程学报,2011,31(28):65-70.SUN Xiaofeng,ZENG Jian,ZHANG Fang,et al.Site selection strategy of discrete frequency resistive active power filter[J].Proceedings of the CSEE,2011,31(28):65-70.
[26]曾正,杨欢,赵荣祥.多功能并网逆变器及其在微电网中的应用[J]. 电力系统自动化,2012,36(4):28-34.ZENG Zheng,YANG Huan,ZHAO Rongxiang.Multi-functional grid-connected inverterand itsapplication in microgrid[J].Automation of Electric Power Systems,2012,36(4):28-34.
[27]RODRÍGUEZP,LUNA A,CANDELA I,etal.Multiresonant frequency-locked loop for grid synchronization of power converters under distorted grid conditions[J].IEEE Transactions on Industrial Electronics,2011,58(1):127-138.

