三齿枞树型叶根轮槽型线优化设计

谈 伟，李文福

(上海汽轮机厂有限公司，上海 200240)

叶片是汽轮机的关键零件，制造工艺精细，其结构设计、振动强度及运行方式对机组的安全可靠性而言至关重要，尤其是末几级长叶片。汽轮机末几级长叶片和叶根轮槽在运行过程中受离心力和激振力的作用，在叶片表面和叶根槽变截面处易产生极大的应力，导致发生叶片断裂或叶根槽开裂的情况[1]。近年来，随着汽轮机产业的发展，小功率、高转速类汽轮机市场不断扩大，叶片所受的载荷也不断增加，这对叶根和轮槽的强度提出了更高的要求。枞树型叶根具有承载能力强、强度适应性好、拆装方便等优点[2]，在汽轮机中的应用越来越广。

随着火力发电汽轮机市场的饱和，联合循环、太阳能汽轮机等市场快速发展，相应地要求汽轮机频繁启停，这对末几级叶片的低周疲劳强度提出了更高的要求。叶片的启动停机过程是导致裂纹萌生和稳态扩展的主要因素，而直接反映叶片低周疲劳程度的就是叶根轮槽的峰值应力。叶片的低周疲劳强度随着峰值应力的降低，会呈指数增加[3]。随着计算机辅助设计手段的不断发展，在汽轮机叶片设计开发过程中采用各种有限元计算方法，日益显现出高效率、低成本的优势，有限元方法已经成为叶片设计开发流程中不可或缺的环节[4-7]。许多研究者和工程师基于此方法，提出了多种优化叶根、轮槽的方法[8-9]。这些方法均采用遗传算法来完成叶根轮缘型线的多变量优化，但尚处于理论计算的阶段。本文在此类方法基础上，结合多个工程进行可用性分析，形成了完整的叶根轮槽工程图纸。本文主要利用有限元法对三齿枞树型叶根进行优化设计，以减小叶根、轮槽处峰值应力为目标，对原有的两种叶根轮槽的关键尺寸进行了优化设计，最终获得了轮槽峰值应力更低的叶根轮槽型线。并对新叶根的可用性进行了分析，将其成功应用于工程项目。

1 叶根优化过程

本次设计主要是针对工程项目进行优化，局限较多。采用多次手动优化型线的方式，利用ABAQUS商用软件进行计算分析，获得优化型线。本文分析的枞树型叶根轮槽型线如图1所示。根据以往的工程经验可知，叶根的峰值应力位于R1处，轮槽的峰值应力位置位于R2处。首先根据几何关系和约束关系建立叶根的参数化模型，并进行计算分析。优化的目的是降低叶根和轮槽的峰值应力，并考虑工程应用的可行性，控制第3对齿颈部宽度L的最小极限，最终获得新的结构型线。

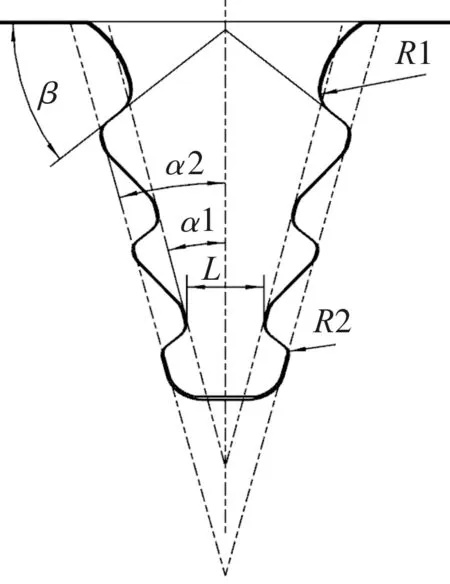
图1 叶根轮槽的截面型线图

本次优化需保证叶根、轮槽接触面与过渡圆角之间的角度，以防止出现应力集中。通过调整接触面角度β并配合R1和R2的大小变化，调整叶根的关键尺寸辐射角α1、α2来适应接触角度的变化，控制圆弧段和直线段的相切约束条件以及叶根轮槽的非接触面的间隙，经过多次计算分析，获得最终的叶根轮槽型线。优化前后的叶根轮槽型线如图2所示，关键尺寸如表1所示。

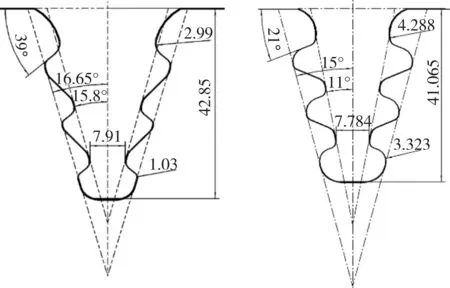
(a)优化前 (b)优化后

图2 优化前后叶根轮槽型线

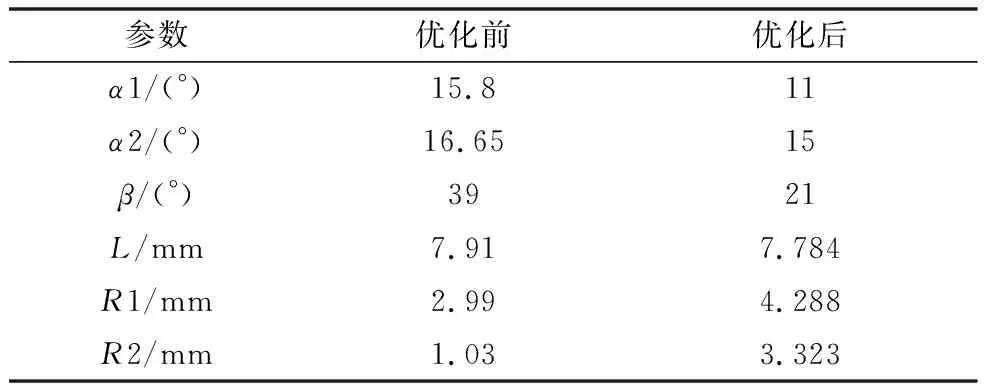
表1 叶根轮槽型线优化前后关键尺寸对比

2 优化叶根数值分析

2.1 计算模型

与此叶根相匹配的叶片叶高为500 mm，本文采用该叶片进行应力分析，叶根处的计算模型如图3所示。两个模型仅叶根不同，中间体、叶身、围带和凸台等均完全相同，轮槽的高度也相同。

(a)优化前 (b)优化后

图3 叶片叶根计算模型

2.2 网格划分及边界条件

本文采用全六面体网格和五面体网格对两种叶根进行划分，单元类型为C3D8I，如图4所示。中间体以上部分网格完全相同，为全六面体网格，单元数为23 077个，优化前叶根单元数为71 450个，轮槽单元数为76 400个，优化后叶根单元数为95 100个，轮槽单元数为90 750个。此外，对两种叶根轮槽的接触区域进行了网格加密，其网格尺度相同。叶片轮槽的材料属性如表2所示，边界条件如图5所示，采用线弹性的方法进行分析计算，模拟叶片的受力情况。

(a)优化前叶根

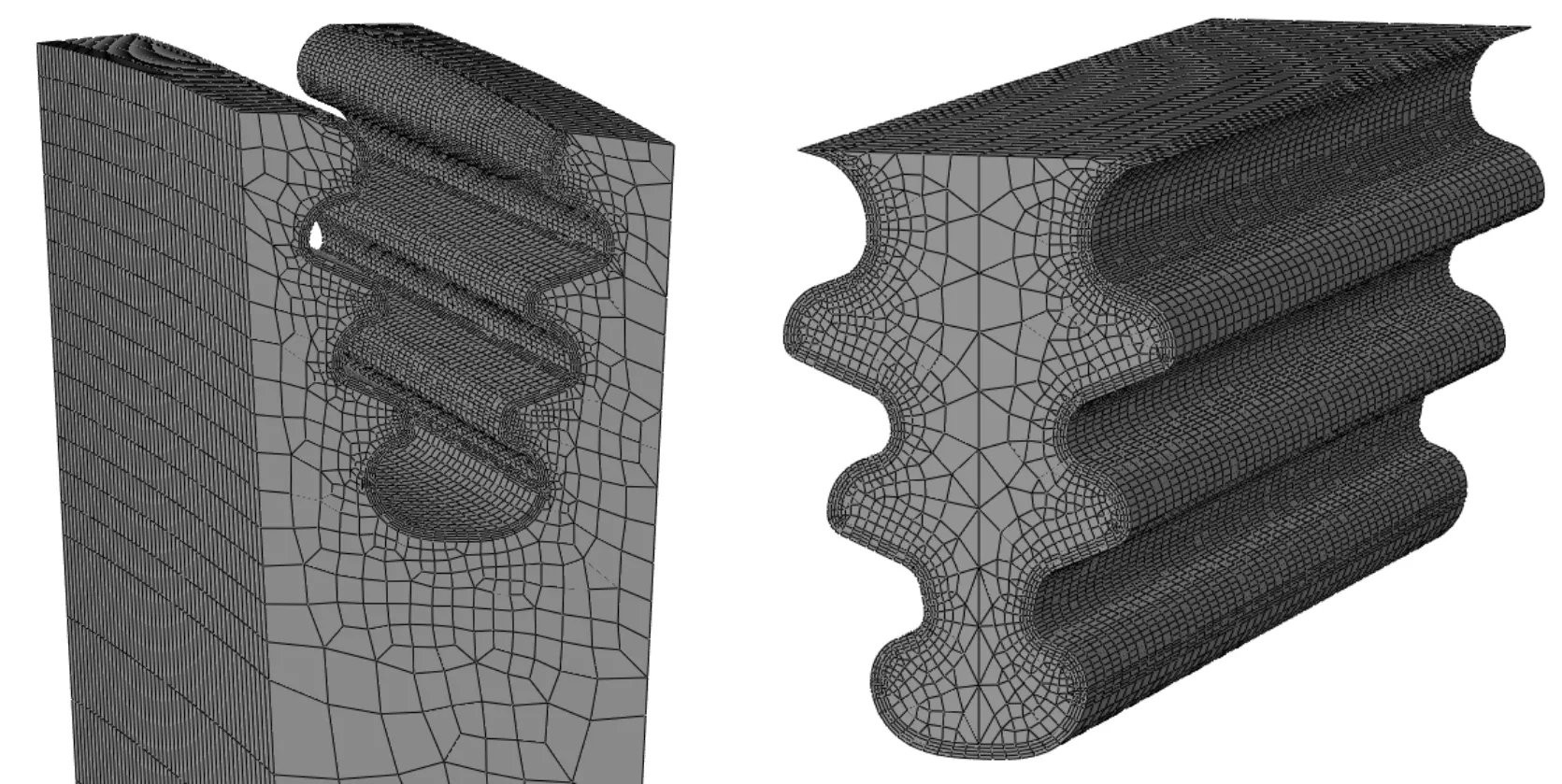
(b)优化后叶根

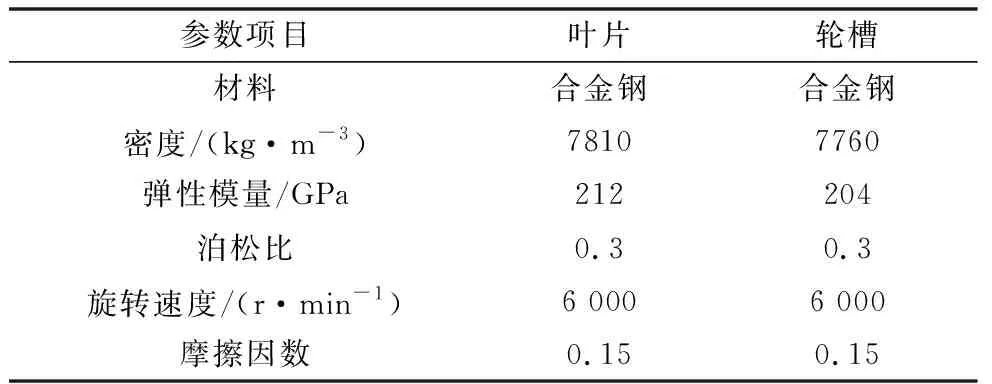
表2 叶片轮槽的材料属性

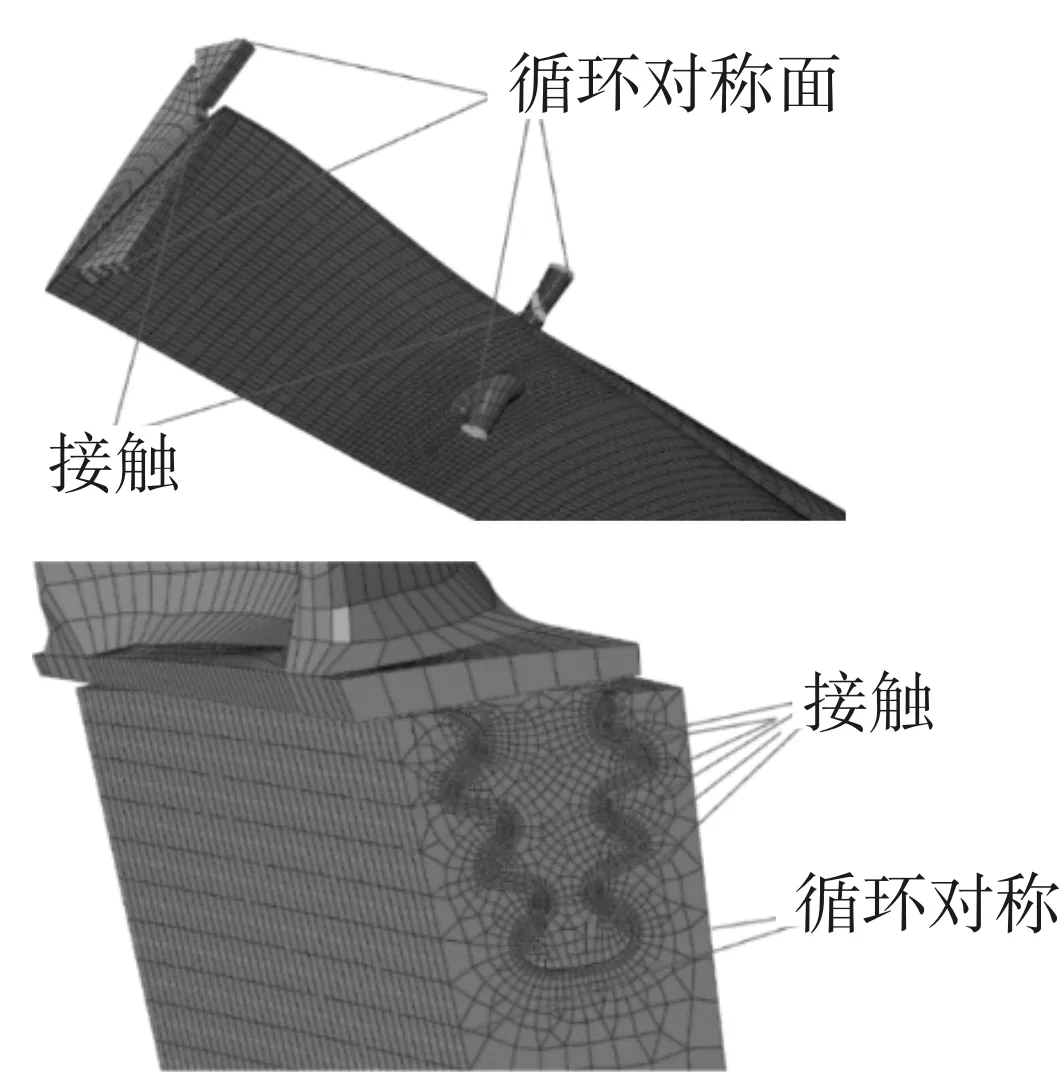
图5 边界条件示意

2.3 结果分析

本文采用三维有限元接触应力分析方法，对比了优化前后的叶根轮槽的等效应力。图6给出了两种叶根的等效应力分布情况，左侧是内弧侧，右侧是背弧侧。可以看出，两种叶根的应力分布趋势相同，同一对齿的背弧侧的应力均大于内弧侧的应力，第1对齿的应力最大，第2、3对齿的应力逐渐减小。由于叶片是弧形的，背弧侧的受力较大，故背弧侧的应力值较大，同理，内弧侧叶片进出汽边位置对应的叶根应力也较同侧其他位置的应力大。优化前叶根的峰值应力为1 190 MPa，优化后叶根的峰值应力为1 265 MPa，应力水平基本相当，优化后第1对齿应力较大区域面积变大，这是优化后第1对齿的圆角增大，圆角径向分布范围变大导致的，第2、3对齿的应力较大区域面积较优化前明显变小，总体来看，优化后叶根的应力水平与优化前相当。

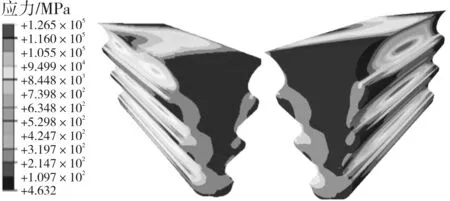
(a)优化前

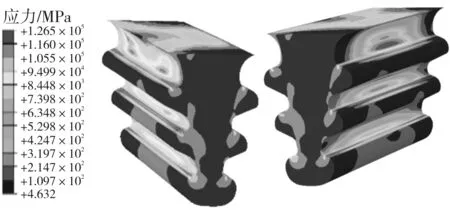
(b)优化后

图6 叶根的应力分布云图

两种叶根对应轮槽的应力分布如图7所示，左侧是内弧侧，右侧为背弧侧。可以看出，两种轮槽的应力分布趋势也基本相同，从第1对齿到第3对齿应力逐渐增加，背弧侧的应力较内弧侧稍大，这也是由叶片形状和重心的分布导致的。优化前轮槽的第3对齿的应力为1 514 MPa，优化后轮槽的应力为999.5 MPa，明显小于优化前，且优化后轮槽的3对齿应力值变化梯度优于优化前的轮槽。优化后轮槽的应力整体明显优于优化前，峰值应力下降约50%。

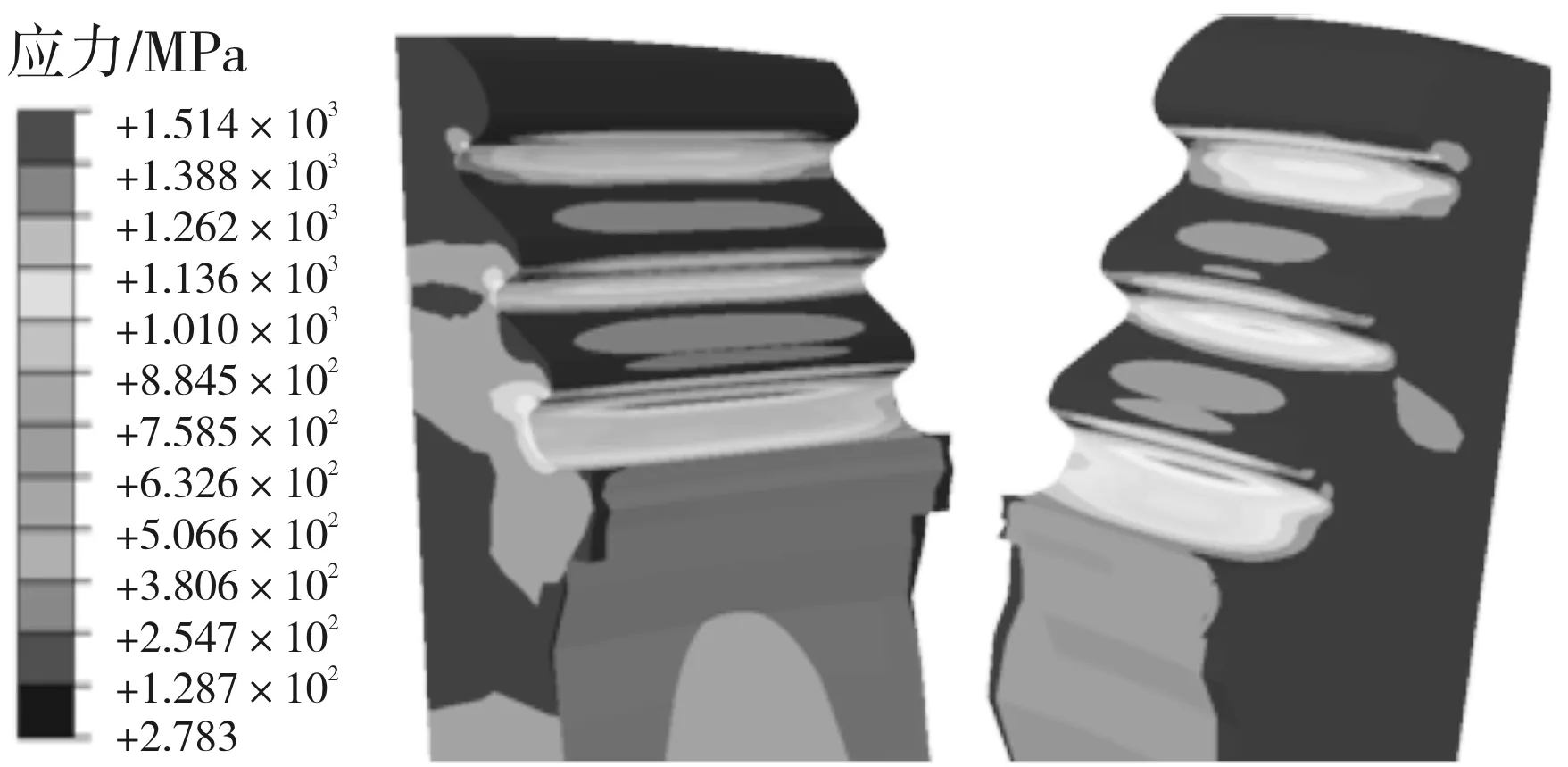
(a)优化前

(b)优化后

图7 两种轮槽的应力分布云图

从以上计算结果可知，优化后得到的叶根和轮槽的3对齿应力分布均较为合理。优化前叶根轮槽3对齿的应力变化梯度较大，不利于保证叶片运行的安全可靠性，而优化后轮槽应力较优化前下降了约50%。此外，从结果可以看出，叶根和轮槽的最大应力均处于背弧侧，可适当地改变叶身的重心，使叶根轮槽两边的应力水平趋于一致，降低叶根轮槽的峰值应力。本文优化得到的叶根应力分布合理，但需要进一步分析实际产品的可用性。

3 可用性分析

为了实现叶根轮槽的工程应用，本文采用二维有限元应力分析方法对比了叶根的应力集中因数和叶根轮槽的相对滑移量，采用三维有限元应力分析方法分析了叶根轮槽的配合间隙及其对叶片振动的影响。

3.1 应力集中分析

叶根应力集中因数是叶根颈部的最大应力和平均应力的比值，将应力集中因数的计算简化为平面应力问题进行分析，优化前后的叶根计算模型如图8所示。叶根的网格尺寸为0.1 mm，轮槽型线部分的网格尺寸为0.1 mm，其余边网格尺寸为5 mm，两个轮槽的大小相同。

(a)优化前 (b)优化后

图8 应力集中因数计算模型

在轮槽底部设定固支约束，叶根顶部加载相同的离心力，根据应力集中因数的计算公式分别对两种叶根的3对齿颈部位置进行分析。表3给出了两种叶根的3对齿的应力集中因数。从结果可知，优化后第1齿和第2齿的应力集中因数下降，第3齿略有上升，这是第3齿的颈部宽度变窄，峰值应力有所上升所致。

表3 两种叶根的应力集中因数对比

3.2 叶根轮槽相对滑移量分析

由于叶根轮槽位移存在矢量关系，不能直接对比总滑移量，为了准确地反映叶根轮槽的相对滑移量，分别对叶根和轮槽的同一静态接触点的3对齿的3个方向(U1，U2，U3)的平均滑移量进行提取，再进行矢量叠加，得到叶根轮槽的相对总滑移量，计算示意图如图9所示。

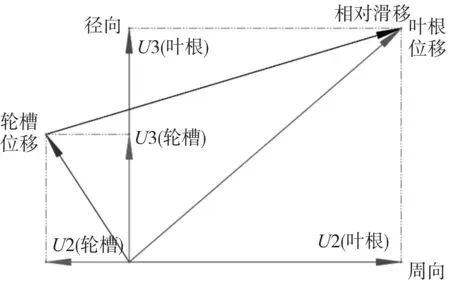
图9 叶根轮槽相对滑移量计算示意

表4给出了两种叶根的相对滑移量计算结果。从结果可看出，优化后叶根轮槽的相对滑移量明显减小，这是因为优化后叶根的接触面角度β更小，叶根相比优化前更难发生径向滑动，叶根和轮槽的有效接触面积更大，更能够保证叶片的安全运行。

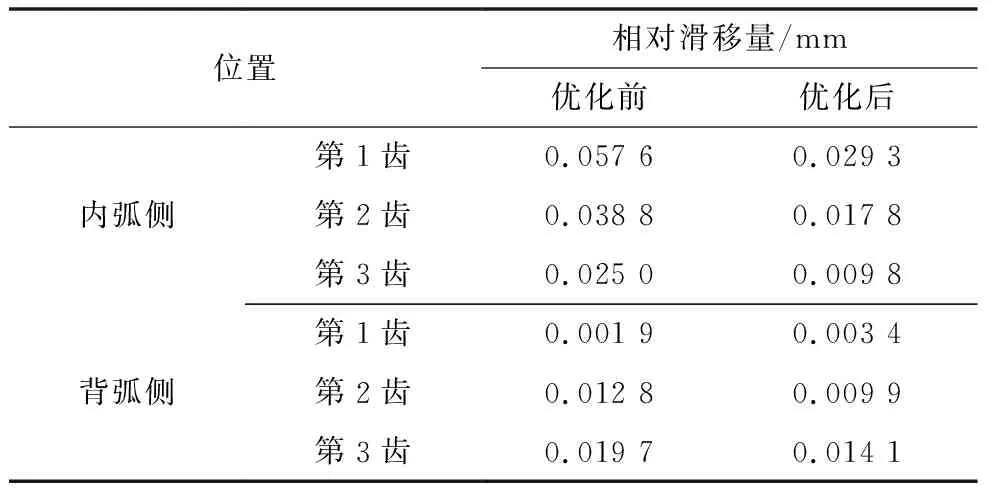
表4 叶根轮槽的相对滑移量

3.3 两种叶根对叶片频率的影响

利用有限元方法对叶片的频率进行摄取，计算模型和应力分析计算模型相同，仅在叶根、轮槽的接触面定义tie约束，计算结果如图10所示。从结果可看出，叶根优化后叶片的频率变化很小。因为叶片的频率直接影响机组运行时的叶片振动，这就说明叶根优化对叶片的振动影响很小。

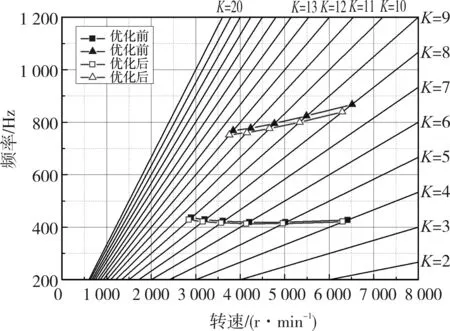
图10 叶根优化前后叶片频率

3.4 叶根轮槽配合间隙分析

各对齿的配合间隙计算过程如下：假设第1对齿存在间隙，计算第2对、第3对齿的峰值应力，然后试算第1对齿不同间隙，保证第1对齿承担主要离心力作用，即峰值应力出现在第1对齿位置；同理计算第2、3对齿的配合间隙，根据工程经验，第2、3对齿的配合公差相同。多次循环试算不同的配合间隙，并考虑目前加工制造的限制，最终确定配合间隙为：第1对齿间隙0.016 25 mm，第2、3对齿间隙0.026 25 mm。表5给出了不同配合状态下叶根和轮槽的应力峰值，根据以往的工程经验，此配合间隙能够保证机组安全运行。

最终根据以上分析，得到了型线优化和配合间隙优化后的三齿枞树型叶根的工程图纸。通过模化，叶根已形成系列，该系列叶根已用于多个实际工程项目，部分机组已投运。

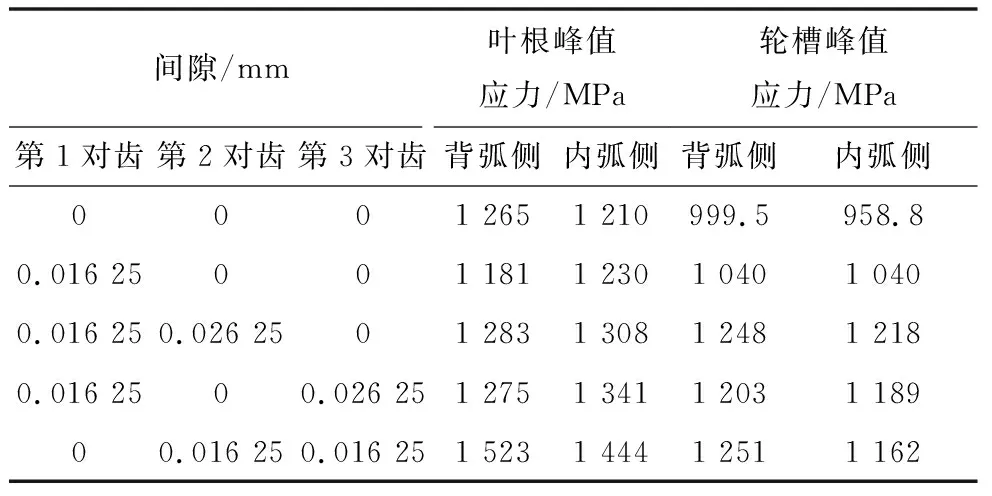
表5 不同配合间隙下叶根轮槽峰值应力

4 结 论

本文基于现有的三齿枞树型叶根，针对叶根轮槽的峰值应力进行优化，配合调整了接触面角度、叶根辐射角以及第3齿的颈部宽度，经过多次优化，最终得到优化后的叶根型线。分析结果表明：

1)优化后，叶根的应力水平基本不变，轮槽的峰值应力较优化前下降约50%，明显优于优化前叶根型线，优化目的达成；

2)优化后叶根第1、2齿的应力集中因数优于优化前，第3齿的应力集中因数略差于优化前；

3)由于接触角度变小，优化后叶根轮槽的相对滑移量较小，叶根和轮槽的有效接触面积更大，安全性更高；

4)优化方案对叶片频率的影响很小，因此可忽略对叶片振动的影响。

通过对叶根轮槽配合间隙的分析，确定了最终叶根轮槽的工程图纸。目前该优化方案已应用于多个实际工程项目。