接地式三要素型动力吸振器的Ｈ∞优化*

王孝然 申永军杨绍普

（石家庄铁道大学机械工程学院，石家庄 050043）

接地式三要素型动力吸振器的Ｈ∞优化*

王孝然 申永军†杨绍普

（石家庄铁道大学机械工程学院，石家庄 050043）

以一种接地式三要素型动力吸振器为对象，研究了基于H∞优化准则的系统参数最优解析解.首先，将串联型粘弹性模型引入到接地式的动力吸振器中，并建立了运动微分方程，得到了系统的解析解.随后，以系统的解析解为研究对象发现该系统存在着三个固定点，利用固定点理论将三个固定点调到了同一高度得到了动力吸振器的最优调谐比和最优刚度比设计公式，并依据H∞优化准则通过最小化幅频曲线的最大值得到了系统最优阻尼比设计公式.最后，通过数值解与解析解的对比说明了解析解的正确性，并证明了接地式三要素型动力吸振器有较好的吸振效果.

动力吸振器， 固定点理论，H∞优化， 参数优化

引言

振动是生产和生活中的一种常见现象.随着运动速度不断提高，机械设备的振动问题越来越受到人们的关注.尤其在农业机械领域，振动不仅容易引起农业机械的疲劳损伤，影响设备的寿命，还会降低仪器仪表的测量精度，导致继电器等电气部件和自控系统工作失灵.同时振动还不可避免地产生噪音，影响操作人员的正常工作甚至危害健康.为了抑制有害的振动，长期以来人们开展了大量的研究，提出了缓冲隔振、阻尼减振、动力吸振等多种振动控制技术.文献［1］研究了拖拉机前桥悬架参数匹配及其对振动特性的影响，能够很好地降低拖拉机的振动.文献［2］研究了悬挂农具对电液悬挂系统拖拉机振动的影响，为拖拉机主动减振控制提供了理论依据.文献［3］研究了农具质量对拖拉机悬挂农具系统振动特性的影响，为拖拉机减振系统的设计提供了重要参考.文献［4］分析了行星排式混合动力汽车传动系扭转振动，为混合动力汽车的振动及噪声性能改善提供参考.文献［5］研究了车厢壁面振动对其内部声场的影响度分析与阻尼降噪，并试用阻尼减振方法，对以正影响度为主的壁面粘贴阻尼材料，使耳旁噪声降低了2.2dB（A）.

动力吸振器又称调谐质量阻尼器，自1909年Frahm［6］发明了第一个动力吸振器以来，人们对其研究已有一百多年的历史.这种无阻尼的动力吸振器虽然当外激励频率与主系统频率相等时会取得很好的减振效果，但在附加吸振器后，主系统会出现两个新的共振频率.一旦激励频率偏离主共振频率时就有可能再次引起较大的共振幅值，所以说该模型适用频率范围非常窄.1928年，Den Hartog和Ormondroyd［7］发现在无阻尼动力吸振器中加入适当的阻尼会拓宽动力吸振器的减振频率.现在该模型通常被称为Voigt型动力吸振器而且已经被视为动力吸振器的经典模型.

除了Voigt型动力吸振器，人们也研究了许多其他形式动力吸振器.典型的如2001年Ren等人［8］提出了一种接地式动力吸振器模型，该模型中阻尼器并不是连接在主系统和子系统之间，而是直接连接子系统和结构（或者地基）.Ren等人对其参数进行了优化，与Voigt模型的对比说明了该模型具有更好的减振效果.2005年Liu［9-10］等人对该模型采用另一种方法进行了参数优化，并在2010年对主系统含阻尼的情况通过固定点存在的假设得到了近似最优参数.由于振动控制工程中大量采用粘弹性材料，而粘弹性材料不仅具有阻尼性质也具有刚度性质，日本学者Asami等［11-12］提出了三要素动力吸振器模型并对其进行了优化设计，发现在相同质量比情况下，该模型具有更好的减振效果.文献［13-14］研究了时滞对动力吸振器的影响，给出了如何利用时滞提高振动控制效果的思想.文献［15-16］研究了四种半主动动力吸振器的近似解析解，并分析了半主动动力吸振器的参数设计和时滞对半主动控制规律的影响.文献［17-18］研究了宽带动力吸振器优化设计.文献［19］研究了连续型参数吸振器的优化设计.文献［20］研究了一种含负刚度元件的新型动力吸振器的参数优化.

本文研究了一种接地式三要素型动力吸振器，应用H∞优化方法对该动力吸振器进行动力学分析和参数优化，得到了最优调频比、最优刚度比和最优阻尼比的设计公式.并通过分析比较验证了该吸振器的振动控制效果.

1 基本模型及解析解研究

如图1所示为本文研究的接地式三要素型动力吸振器模型，其中，m1代表主系统质量，m2代表动力吸振器质量，k1和k2分别代表主系统和动力吸振器的刚度，ka和c分别是串联型粘弹性模型的刚度和阻尼，F0和ω分别表示激振力振幅和频率，x1、x2、x3分别表示主系统、动力吸振器以及串联弹簧和阻尼分割点的位移.

图1 接地式三要素型动力吸振器模型Fig.1 Model of grounded three-element type dynamic vibration absorber

根据牛顿第二定律可以得到系统的动力学方程

2 最优频率比和最优刚度比

由式（6）通过简单推导，可以证明其归一化的幅频曲线都将通过三个独立于阻尼比的点，这三个点称为该动力吸振器的固定点.为了直观说明该结论，图2给出了阻尼比为0、0.276和∞时的归一化幅频曲线.从图中可以清楚地看出曲线均通过P、Q和R三点.因为固定点与阻尼比无关，为了解出固定点，只需令

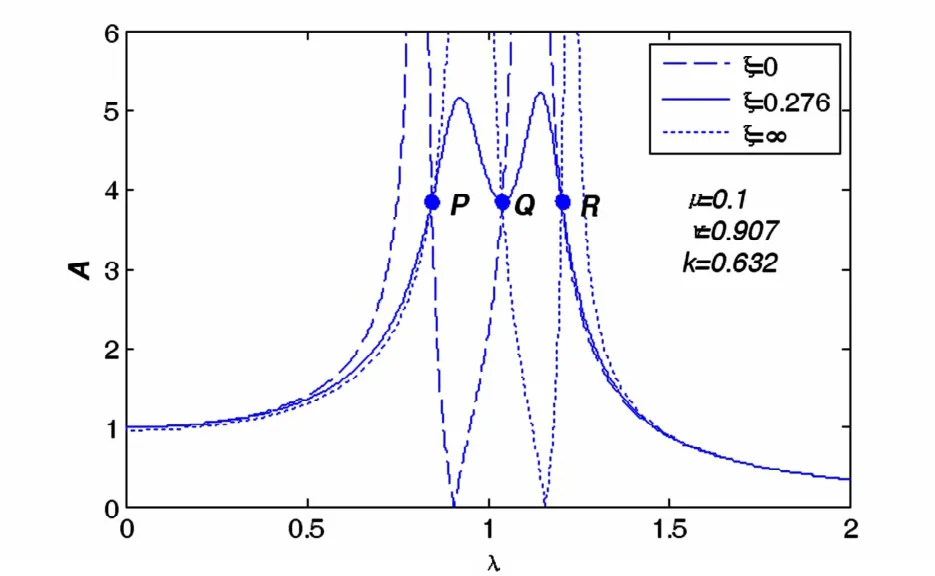
图2 不同阻尼比下幅频曲线Fig.2 The amplitude-frequency curves under different damping ratios

当把三个固定点的纵坐标调到同一高度，就可以得到最优调频比.这个调整需要两步完成.第一步把P点和R点的纵坐标调到同一高度，可以得到

把（15）式代入到（9）式可以得到

由（16）式解得

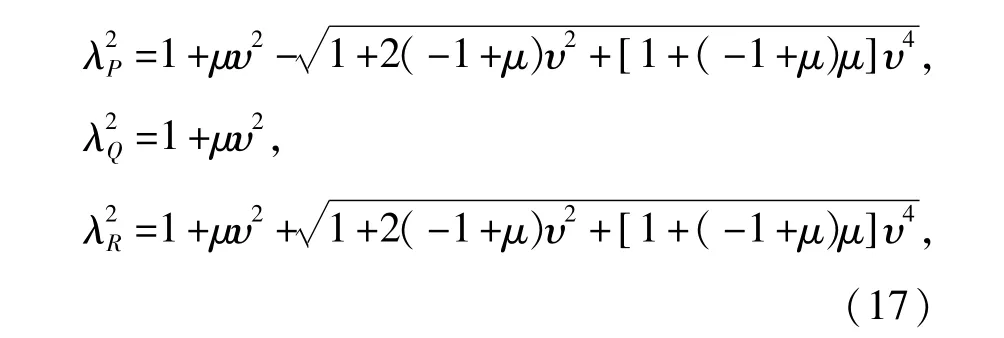
式（14）可以写成

第二步，把P或R点与Q点的纵坐标调整到同一高度，可以得到最优频率比

把（19）式代入到（15）式得到

此时，

3 最优阻尼比

当把三个固定点调整到同一高度后，如图3所示.此时改变阻尼比，可以改变共振峰的高度，最优阻尼比可以通过调整两个共振峰为同一高度时实现.

为了得到最优阻尼比，需要知道在两个共振峰处的横坐标，即λ1，2.令

由上式可以得到ξ1和ξ2的值，然后得到但是这样很难得到解析结果.

图3 不同阻尼比下的幅频曲线Fig.3 The amplitude-frequency curves under different damping ratios

由图3我们可以清晰地观察到当两个共振峰在同一高度时，Q点的附近正好是幅频曲线斜率为零的区域，Q点的横坐标已经求出，可以根据Q点的横坐标得出近似的最优阻尼比.

根据

从而得到近似最优阻尼比

图4给出了根据前述优化结果得到的幅频曲线，可以发现基本达到了优化目的.

图4 近似最优阻尼比时的幅频曲线Fig.4 The amplitude-frequency curve under approximate optimal damping ratio

4 数值验算

为了验证前文得到结果的正确性，任选激励幅值为F＝1000，选取质量比为μ＝0.1，从而根据前述结果得到其他系统参数为k＝0.632，v＝0.907，ξ＝0.2765.利用四阶龙格库塔法，选取计算时间为100倍的激励周期，可以得到给定激励频率下系统响应的数值解.略去瞬态响应，取稳态解的最大值为响应幅值可以得到归一化的幅频曲线，如图5中圆圈所示.根据式（6），图5中也同时用实线画出了系统解析解的曲线.从图中可以明显看出，与图3未优化结果相比较，通过优化使其两个共振峰处于相等高度.同时数值解与解析解的吻合，也说明了本文求解过程的正确性.

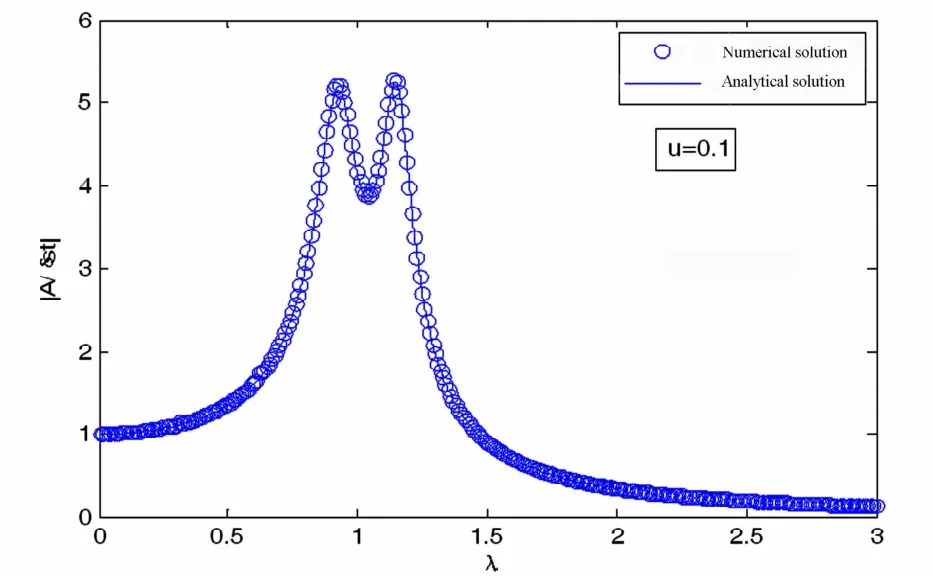
图5 数值解和解析解对比Fig.5 Numerical solution compared with analytical solution

5 结论

本文将串联型粘弹性模型引入到接地式的动力吸振器中，并以其为研究对象根据固定点理论得到了系统取得最优减振效果时的动力吸振器参数，通过数值解验证了所得结果的正确性.证明了接地式三要素型动力吸振器有较好的吸振效果.

1 伊力达尔·伊力亚斯，朱思洪，徐刚，袁加奇.拖拉机前桥悬架参数匹配及其对振动特性的影响.农业工程学报，2015，31（10）：29～36（Yilidaer Y L Y S，Zhu SH，Xu G，Yuan JQ.Front axle suspension parametersmatch and its impacton vibration characteristics of tractor.Transactions of the Chinese Society of Agricultural Engineering，2015，31（10）：29～36（in Chinese））

2 承鉴，迟瑞娟，毛恩荣.悬挂农具对电液悬挂系统拖拉机振动的影响.农业工程学报，2015，31（7）：24～32（Cheng J，Chi R J，Mao E R.Influence of hanging farm implement on vibration of tractor with electro-hydraulic hitch system.Transactionsof the Chinese Society of Agricultural Engineering，2015，31（7）：24～32（in Chinese））

3 朱思洪，徐刚，袁加奇，马佳富，伊力达尔，李科.农具质量对拖拉机悬挂农具系统振动特性的影响.农业工程学报，2014，30（24）：30～37（Zhu SH，Xu G，Yuan JQ，Ma JF，Yi Lidaer，Li K.Influence of implement′smass on vibration characteristics of tractor-implement system.Transactions of the Chinese Society of Agricultural Engineering，2014，30（24）：30～37（in Chinese））

4 于海生，张彤，马智涛，王瑞平.行星排式混合动力汽车传动系扭转振动分析.农业工程学报，2013，29（15）：57～64（Yu H S，Zhang T，Ma Z T，Wang R P.Torsional vibration analysis of planetary hybrid electric vehicle driveline.Transactions of the Chinese Society of Agricultural Engineering，2013，29（15）：57～64（in Chinese））

5 刘红光，陆森林，曾发林.车厢壁面振动对其内部声场的影响度分析与阻尼降噪.农业工程学报，2002，18（2）：62～64（Liu H G，Lu S L，Zeng F L.Influence of wall vibration on the sound in a cab and noise reduction with damping.Transactionsof the Chinese Society of Agricultural Engineering，2002，18（2）：62～64（in Chinese））

6 Frahm H.Device for damping vibrations of bodies.U.S.Patent989，958.1911

7 Ormondroyd J，Den Hartog JP.The theory of the dynamic vibration absorber.Journal of Applied Mechanics，1928，50：9～22

8 Ren M Z.A variant design of the dynamic vibration absorber.Journal of Sound and Vibration，2001，245（4）：762～770

9 Liu K，Liu J.The damped dynamic vibration absorbers：revisited and new result.Journal of Sound and Vibration，2005，284（3）：1181～1189

10 Liu K，Coppola G.Optimal design of damped dynamic vibration absorber for damped primary systems.Transactions of the Canadian Society for Mechanical Engineering，2010，34（1）：119

11 Asami T，Nishihara O.Analytical and experimental evaluation of an air damped dynamic vibration absorber：design optimizations of the three-element type model.Journal ofVibration and Acoustics，1999，121（3）：334～342

12 Asami T，Nishihara O.H2optimization of the three-element type dynamic vibration absorbers.Journal of Vibration and Acoustics，2002，124（4）：583～592

13 赵艳影，李昌爱.时滞反馈控制扭转振动系统的振动.物理学报，2011，60（10）114305（Zhao Y Y，Li CA.The delayed feedback control to suppress the vibration in a torsional vibrating system.Acta Physica Sinica，2011，60（10）114305（in Chinese））

14 Zhao Y Y，Xu J.Effects of delayed feedback control on nonlinear vibration absorber system.Journal of Sound and Vibration，2007，308：212～230

15 Shen Y J，Wang L，Yang S P，Gao G S.Nonlinear dynamical analysis and parameters optimization of four semiactive on-off dynamic vibration absorbers.Journal of Vibration and Control，2013，19（1）：143～160

16 Shen Y J，Ahmadian M.Nonlinear dynamical analysis on four semi-active dynamic vibration absorbers with time delay.Shock and Vibration，2013，20（4）：649～663

17 李俊，金咸定.动力吸振器的宽带数值优化设计.振动与冲击，2001，20（2）：16～18（Li J，Jin X D.Broadband numerical optimization design of dynamic vibration absorber.Journal of VIibration and Shock，2001，20（2）：16～18（in Chinese））

18 肖和业，盛美萍，吴伟浩.新型宽带动力吸振器优化设计.振动与冲击，2011，30（1）：98～101（Xiao H Y，Sheng M P，Wu W H.Optimization analysis of new type of broadband dynamic vibration absorber based on particle swarm optimization.Journal of VIibration and Shock，2011，30（1）：98～101（in Chinese））

19 肖和业，盛美萍，雷烨.连续参数型吸振器吸振分析及优化.振动，测试与诊断，2012，32（3）：447～451（Xiao H Y，Sheng M P，Lei Y.Analysis and optimization of continuous parameter type dynamic vibration absorber.Journal of Vibration，Measurement＆Diagnosis，2012，32（3）：447～451（in Chinese））

20 彭海波，申永军，杨绍普.一种含负刚度元件的新型动力吸振器的参数优化.力学学报，2015，47（2）：320～327（Peng H B，Shen Y J，Yang SP.Parameters optimization of a new type of dynamic vibration absorber with negative stiness.Chinese Journalof Theoretical and Applied Mechanics，2015，47（2）：320～327（in Chinese））

H∞OPTIM IZATION OF THE GROUNDED THREE-ELEMENT TYPE DYNAM IC VIBRATION ABSORBER*

Wang Xiaoran Shen Yongjun†Yang Shaopu
（Department of Mechanical Engineering，Shijiazhuang Tiedao University，Shijiazhuang050043，China）

Taking a new type of the grounded three-element type dynamic vibration absorber as the research object，the optimal analytical solution is studied based on H∞optimization principle in this paper.Firstly，a series viscoelasticmodel is introduced into the grounded dynamic vibration absorber，and the analytical solution of the system is obtained based on the established motion differential equation.Three fixed points are found in the amplitude-frequency curves of the primary system.Moreover，the design formulae for the optimal tuning ratio and the optimal stiffness ratio of the dynamic vibration absorber are developed by adjusting the three fixed points to the same height according to the fixed point theory.Then，the optimal damping ratio is obtained by minimizing the maximum value of the amplitude-frequency curves according to H∞optimization principle.In addition，the comparison between the numerical solution and the analytical solution is investigated.It verifies the correctness of the analytical solution，and illustrates that the grounded three-element type dynamic vibration absorber exhibites better performance of vibration absorption.

dynamic vibration absorber， fixed point theory， H∞optimization， Parameter optimization

10.6052／1672-6553-2015-82

2015-11-11收到第1稿，2015-11-16收到修改稿.

*国家自然科学基金（11372198）、河北省高等学校创新团队领军人才计划（LJRC018）、河北省高等学校高层次人才科学研究项目（GCC2014053）、河北省高层次人才资助项目（A201401001）

†通讯作者E-mail：shenyongjun＠126.com

Received 11 November 2015，revised 16 November 2015.

*The project supported by the National Natural Science Foundation of China（11372198），the Cultivation plan for Innovation team and leading talent in Colleges and universitiesof Hebei Province（LJRC018），the Program for advanced talent in the universitiesofHebei Province（GCC2014053），and the Program for advanced talent in Hebei Province（A201401001）

†Corresponding author E-mail：shenyongjun＠126.com