一类非线性金融系统的数值研究*

凯歌张伟

（1.北京工业大学机电学院，北京 100124）（2.内蒙古财经大学统计与数学学院，呼和浩特市 010070）

一类非线性金融系统的数值研究*

凯歌1，2张伟1†

（1.北京工业大学机电学院，北京 100124）（2.内蒙古财经大学统计与数学学院，呼和浩特市 010070）

利用数值模拟的方法研究了一类非线性金融系统的动力学行为.建立了由生产、资金、股份、劳动力四个部分构成的一类非线性金融系统的动力学模型.首先运用四维微分方程来描述由利率、投资需求、价格指数和平均利润率构成的四个状态变量随时间的变化，然后将金融系统简化为四维自治微分方程组.通过对四维自治微分方程组进行数值模拟发现了非线性金融系统的动力学特性，从数值模拟获得的三维相图反映了金融系统的非线性特性.从数值模拟结果发现，在特定的条件下非线性金融系统存在周期运动和混沌运动.除此之外，还观察到参数的改变对四维自治金融系统的非线性特性有着显著的影响.

非线性经济学， 混沌金融系统， 复杂的动力学行为， 混沌运动， 经济动力学

引言

金融系统是一个由众多要素组成的，是开放的，远离平衡态的极其复杂的非线性系统.在这个非线性系统中，随着各种参数的变化，系统的运动状态由于失稳而出现混沌状态是相当普遍的现象.

近年来，非线性经济学在当代经济学中已成为研究热点.非线性经济学领域的研究迅速发展，并成为非线性问题的研究领域中非常活跃的问题之一.非线性经济动力学理论分析有助于预测和解决经济市场中存在的一些非线性问题，对于非线性经济学领域的研究具有重要的理论和实践意义.

1980年，美国经济学家Stutzer［1］首次在Havvelmo经济增长方程中揭示了宏观经济系统的混沌现象，使人们认识到建立在传统经济学理论基础之上的经济模型的局限性，并且最早将混沌模型应用于经济学［3-4］.

最近十年，很多专家研究了非线性经济学.Stutzer［1，3］发现，在宏观经济系统的经济增长方程中存在着混沌现象.他们的研究使人们认识到了传统经济理论基础上的经济模式的局限性.此后学者们开始应用混沌理论来研究经济学.马和陈［4］研究了分岔拓扑结构及一类非线性金融系统的全局复杂性.Ishiyama和Saiki［5］研究了嵌入在混沌吸引子中的不稳定轨道和混沌经济增长周期.建立宏观经济增长周期模型，解决了嵌入在混沌吸引子中的定性和定量相关的不稳定周期解.陈［6］运用数值模拟分析复杂的动力学特性，如周期性、准周期性和金融系统的延时反馈中的混沌行为等.Jian［7］利用全局指数吸引集和Lyapunov稳定性理论的定义研究了很多金融系统的全局指数吸引集和同步问题.Zhao［8］利用Lyapunov稳定性理论和Routh-Hurwitz标准研究了三维混沌金融系统的全局渐进同步策略.Yu［9］运用数值模拟分析了混沌金融系统的平衡、稳定、混沌吸引子、Lyapunov指数及分岔.Cantore和Levine［10］研究宏观经济学中具有评估参数的重新参数化模型，得出重新参数化的方法与标准是等效的.王［11］和邱等人［12］指出非线性动力学可以研究黄金价格的波动、及其导致国际黄金价格总水平变动的主要因素，对金融危机具有预测、预警的作用.张伟等人［13-14］指出非线性动力学不仅涉及学科发展的前沿问题，还涉及了国民经济发展的国家重大工程建设关键技术问题.马等人［15］建立了一类复杂动态宏观经济系统，研究了时间延迟影响到储蓄率及动态金融稳定性.

本文建立了一类具有混沌特性的非线性金融学系统的动力学模型，运用非线性理论和方法研究了金融系统的动力学行为.通过数值方法，运用计算机软件MATLAB来研究非线性金融系统中的周期运动、拟周期运动及混沌运动.经过研究发现当改变金融系统的参数时，能得到不同的周期运动及混沌运动行为.

1 金融系统的非线性动力学方程

基于Jian［7］的研究，金融系统由四个子模块组成，分别为：生产、资金、股份及劳动力，它们由三个一阶微分方程表示.该系统描述了三个状态变量的时间变化：利率x、投资需要y及价格指数z.从经济学的角度出发，影响利率的因素不仅与投资需求和价格指数有关，而且与平均利润率也息息相关.并且平均利润率和利率之间成正比.因此对于金融系统给出如下方程［9］

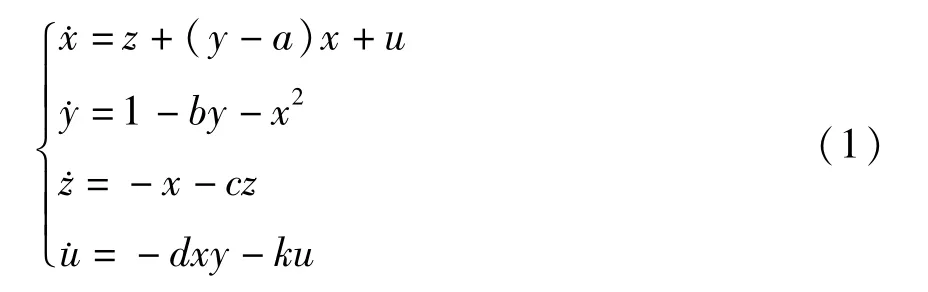
其中u表示平均利润率，a是存储量，b是投资增长率，c是供求系数，参数d和k是为正的常数.

金融系统的非线性动力学行为表现为不同的周期运动及混沌运动.周期运动、混沌运动响应可通过几种常规标准来确定，如波形、相图、功率谱、Poincare图和分岔图等.在本文中，上述判断标准将被用来说明金融系统中的周期运动与混沌运动的存在性.

2 四维超混沌金融系统的动力学分析

四维混沌映射经过初步设计后，还需要数学分析和数值模拟来分析其动力学特性，证明该映射是超混沌映射，同时说明金融系统中的周期运动与混沌运动的存在性.

2.1 吸引子的耗散性及有界性

当a＝0.1，b＝0.2，c＝1.2，d＝0.1，k＝0.15时，四维系统（1）的散度是

所以当a+b+c+k＞0时，可知该映射系统是一个耗散系统.系统的相体积元以指数率收缩，随着t→∞，系统的轨线会渐变演化到一个不变的吸引子集合中.从而说明吸引子的存在性.

即体积元V0在时刻t时收缩为体积元V0e-（a+b+c+k）t.这意味着，当t→∞时，包含系统轨线的每一个体积元以指数率-（a+b+c+k）收缩到0.因此，系统轨线最终会被限制在一个体积0的集合上，且它渐进运动固定在一个吸引子上.

2.2 映射的平衡点及其稳定性的分析

四维超混沌系统（1）的平衡点满足方程（2）

当参数a，b，c，d，k满足

超混沌系统（2）有三个平衡点：

在平衡点P0（0，1／b，0，0）的Jacobi矩阵为

用MATLAB软件很容易证明当

a＝0.1，b＝0.2，c＝1.2，d＝0.1，k＝0.15时，Jacobi矩阵J0特征值为

λ1＝9，λ2＝-0.9，λ3＝-0.1，λ4＝-0.6可知，四维金融系统中P0是一个不稳定的鞍点.

在平衡点P1的Jacobi矩阵为

同理，在平衡点P2处，Jacobi矩阵J2的特征值为

由此，可知新的混沌映射的平衡点都是不稳定的.

3 金融系统参数变化的动力学性质和数值模拟

3.1 金融系统的周期运动

图1说明了当投资增长率为b＝0.2时金融系统发生周期性运动.其他参数和初始条件的选取如下：

a＝0.1，b＝0.2，c＝1.2，d＝0.1，k＝0.15，

x0＝1，y0＝1，z0＝0.6，u0＝0.6.

图1（a）表示在空间（x，y，u）上的三维相图，图1（b）和（c）分别表示平面（x，u）上的二维相图和平面（y，u）上的二维相图，图1（d）和（e）分别表示表示平面（t，x）和平面（t，y）上的波形图.数值计算得到金融系统发生了周期运动.

图1 金融系统的周期运动：（a）-（c）相图，（d）（e）时间历程Fig.1 Periodicmotion of the financial system：（a）-（c）phase，（d）（e）time history

在图2（a）-（e）中，投资增长率b被选为b＝0.15，其他参数和初始条件都与图1相同.通过数值计算得到金融系统发生了拟周期运动.

3.2 金融系统的混沌运动

图3（a）-（e）给出了当投资增长率b减为b＝0.1时，金融系统发生混沌运动，其他参数和初始条件都与图1时的相同.与图2和图3对比发现，当投资成本参数b变小时，相图上会出现差异.

图2 金融系统的拟周期运动：（a）-（c）相图，（d）（e）时间历程Fig.2 Quasi-periodic motion of the financial system：（a）-（c）phase，（d）（e）time history

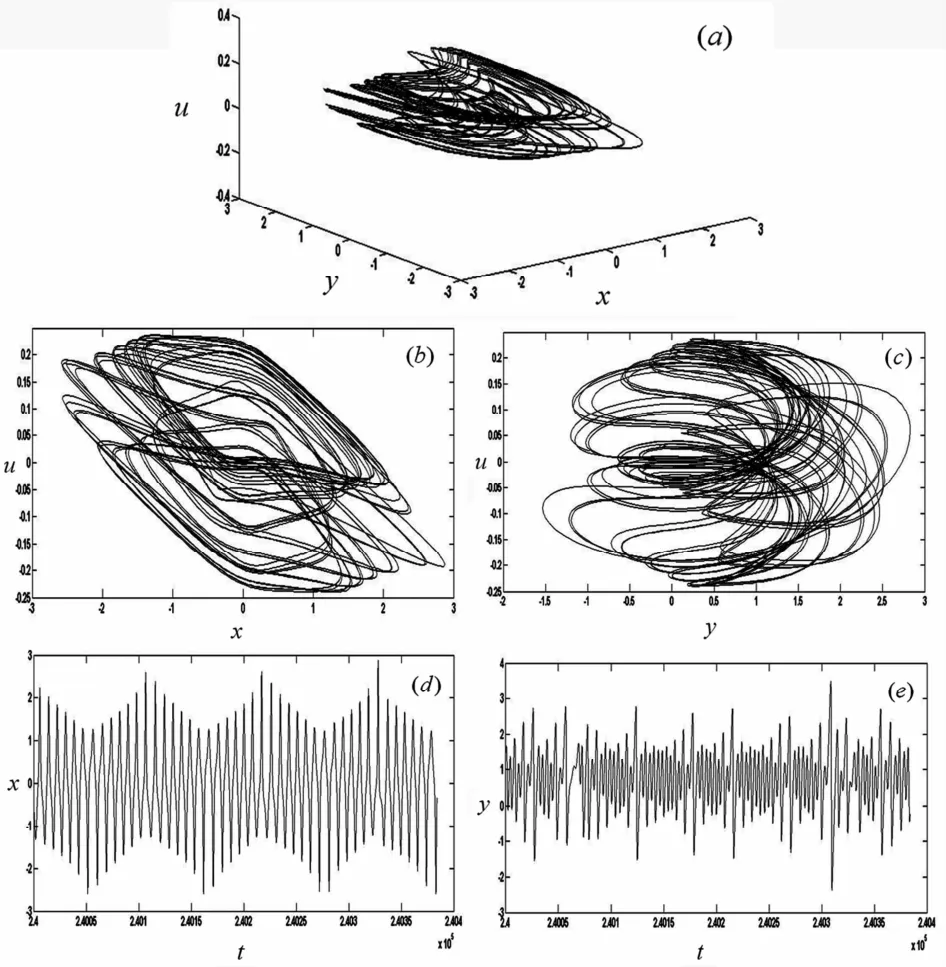
图3 金融系统的第一类混沌运动：（a）-（c）相图，（d）（e）时间历程Fig.3 The first class of chaoticmotion for the financial system：（a）-（c）phase，（d）（e）time history

图4（a）-（e）说明了当投资增长率参数减少为b＝0.05时，金融系统存在混沌运动，其他参数和初始条件与图1相同.从图3和图4的三维相图中可得知，它们的形状完全不同.

图5说明了当投资增长率参数变为b＝0.01时，金融系统存在混沌运动，其他参数和初始条件都与图1相同.从图4和图5三维相图得出，它们的形状是完全不同的.对比图3、图4和图5三维相图可得出，参数b变小时混沌运动的图形也发生变化.

图4 金融系统的第二类混沌运动：（a）-（c）相图，（d）（e）时间历程Fig.4 The second class of chaotic motionfor the financial system（a）-（c）phase，（d）（e）time history

图5 融系统的第三类混沌运动：（a）-（c）相图，（d）（e）时间历程Fig.5 The third class of chaotic motion for the financial system：（a）-（c）phase，（d）（e）time history

基于图1～5可以得知，当投资增长率参数b变化时，此金融系统的动力学行为从周期运动、拟周期运动变为混沌运动.我们推测b＝0.15和b＝0.1之间存在分岔.分岔是系统某一参数连续变化到达某一临界值时，系统的全局性态会发生突然的变化，参数产生两条或更多条的分支.利用Runge-Kutta算法和Poincare映射理论得到分岔图的数值解.在周期运动中，Poincare映射是几个独立分散的点；在混沌运动中，Poincare映射是由被限制在Poincare截面上的点组成的.本文中，我们只运用了波形、相图等几种常规标准来判别金融系统的周期运动及混沌运动的发生.

4 结论

本文利用数值方法研究了一类具有混沌特性的非线性金融学系统的动力学行为.运用计算机软件MATLAB对金融系统进行数值模拟，数值结果给出了对于金融系统的四个一阶微分方程混沌运动的存在性的判断.从数值模拟得出，当选取不同的投资增长率参数b和其他的参数时系统存在周期性运动或者混沌运动的发生，同时也发现混沌运动的相图形状是完全不同的.此外，投资增长率参数b对四维自治非线性系统的非线性动力学行为具有显著的影响.

1 Stutzer M J.Chaotic dynamics and bifurcation in a macro model.Journal of Economic Dynamicsand Control，1980，2（2）：353～376

2 Stutzer M J.The construction of revenue sharing formulae.Journal of Southern Economic，1982，6（3）：55～62

3 Stutzer M J.Nonlinear subsidies：the inefficiency of inkind transfers revisited.Public Finance Quarterly，1984，77（2）：79～95

4 Ma JH，Chen Y S.Study for the bifurcation topological structure and the global complicated character of a kind of nonlinear finance system.Applied Mathematics and Mechanics，2001，22（11）：1240～1251

5 K Ishiyama，Y Saiki.Unstable periodic orbits and chaotic economic growth.Chaos，Solutions and Fractals，2005，26（8）：33～42

6 Chen W C.Dynamics and control of a financial system with time-delayed feedbacks.Chaos，Solutions and Fractals，2008，37（5）：1198～1207

7 Jian JG，Deng X L，Wang JF.Globally exponentially attractive set and synchronization of a class of chaotic finance system.ISNN Part I：LNCS，2009，5551（3）：253～261

8 Zhao X S，Li Z B，Li S.Synchronization of a chaotic finance system.Applied Mathematics and Computation，2011，217（2）：6031～6039

9 Yu H J，CaiG L，Li Y X.Dynamic analysis and control of a new hyperchaotic finance system.Nonlinear Dynamics，2012，67（23）：2171～2182

10 Cantore C，Levine P.Getting normalization right：dealing with‘dimensional constants’in macroeconomics.Journal of Economic Dynamics＆Control，2012，36（19）：1931～1949

11 王娟.基于MRS-GARCH模型的我国黄金现货价格波动研究.财经理论研究，2015（6）：82～90（Wang J.Study on volatility of china′s gold price based on markovswitching GARCH model.Journal of Finance and Economics Theory，2015（6）：82～90（in Chinese））

12 邱济洲，额日敦塔娜.基于VAR模型的黄金价格影响因素分析.财经理论研究，2014（6）：10～18（Qiu JZ，Eridun T.Analysis of influencing factors on gold price based on VAR model.Journal of Finance and Economics Theory，2014（6）：10～18（in Chinese））

13 张伟，姚明辉等.高维非线性系统的全局分岔和混沌动力学研究.力学进展，2013，43（1）：64～90（Zhang W，Yao M H，Zhang JH，Li SB.Study of global bifurcations and chaotic dynamics for high-dimensional nonlinear systems.Advances in Mechanics，2013，43（1）：64～90（in Chinese））

14 吕书锋，张伟.复合材料悬臂外伸板的非线性动力学建模及数值研究.动力学与控制学报，2013，13（4）：288～292（Lu S F，Zhang W.Nonlinear analysis of deploying laminated composite cantilever plates.Journal of Dynamics and Control，2013，13（4）：288～292（in Chinese））

15 Ma JH，Tu H L.Analysis of the stability and Hopf bifurcation of money supply delay in complex macroeconomic models.Nonlinear Dynamics，2014，76（1）：497～508

NUMERICAL STUDY OF A CLASSOF NONLINEAR FINANCIAL SYSTEM*

Kai Ge Zhang Wei†
（Beijing University of Technology，Beijing100124，China）
（College of Statistics and Mathematics Inner Mongolia University of Finance and Economics，Hohhot010070，China）

In this paper，the dynamic characteristics of a class of nonlinear finance system are investigated by means of numerical simulation.Themodel developed in this work is composed of four sub-blocks：production，money，stock and labor force.At first，the developmentof four state variables for the interest rate，the investment demand，the price exponent，and the average profitmargin with the time are described by four dimensional differential equations.The hyper chaotic finance system is simplified as a group of four dimensional autonomous differential equations.The nonlinear dynamic characteristics of the system are then examined by the numerical simulations of four dimensional differential equations.The three-dimensional phase diagrams illustrated the nonlinear characteristics of the financial system.Moreover，the numerical results demonstrated thatunder certain condition，periodic motion and chaoticmotion exist in the nonlinear system.In addition，it is found that system parameters and initial conditions have great influence on the nonlinear dynamical behavior of four dimensional autonomous hyper chaotic systems.

nonlinear economics， chaotic financial system， complex dynamic behavior， chaoticmotion，economic dynamics

10.6052／1672-6553-2016-38

2015-11-3收到第1稿，2016-5-26收到修改稿.

*内蒙古自治区高等学校科学研究项目（NJZY134），内蒙古财经大学校级科研项目（KY1306）

†通讯作者E-mail：sandyzhang0＠yahoo.com

Received 3 November 2015，revised 26 May 2016.

*The project supported by the Inner Mongolia Autonomous Region of Institutions of Higher Learning Scientific Research Projects（NJZY134）and Inner Mongolia University of Finance and Economics University Scientific Research Projects（KY1306）

†Corresponding author E-mail：sandyzhang0＠yahoo.com