用能量法分析体外预压力对简支梁动力性能的二阶效应*

方德平钟明镜

（华侨大学土木工程学院，厦门 361021）

用能量法分析体外预压力对简支梁动力性能的二阶效应*

方德平†钟明镜

（华侨大学土木工程学院，厦门 361021）

精细地考虑了体外筋变形中的二阶项，用能量法推导了体外预应力梁的自振频率，阐明了体外预压力对梁自振频率的效应.计算结果表明：体外预压力压缩软化效应的影响系数，主要取决于转向座的数量.无转向座时，体外筋偏心距损失为最大，影响系数为1，体外预压力的效应与外轴力的效应相同.随着转向座数量的增加，偏心距损失减小，体外筋接近于无粘结筋，影响系数降低至接近于0，即接近于无粘结筋预压力的零效应.当梁转向座的数量≥2时，由于影响系数显著地小于1，可以忽略体外预压力的压缩软化效应.随着体外筋面积和偏心距的增加，梁的第1自振频率增大.不过，体外筋对其他阶自振频率的影响很小，可以忽略.

体外预应力， 简支梁， 自振频率， 能量法， 动力分析， 二阶效应

引言

众所周知，体系外的物体对梁施加的外轴力N产生了压缩软化效应，降低了梁的自振频率.普通简支梁的自振频率：

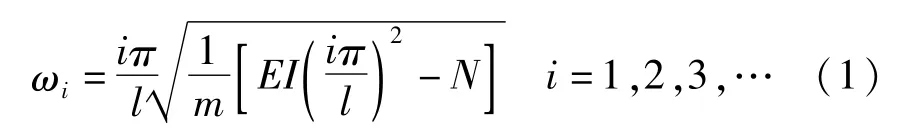
式中，EI为梁的抗弯刚度，m为梁单位长度质量，l为梁的跨度.体外预应力梁动力性能研究中一个有争议的问题是：体外筋对梁的预压力是否影响梁的自振频率？压力产生压缩软化效应，所以本文用预压力这一术语.换一句话说，预压力的压缩软化效应与外轴力的效应是否相同？

Saiidi［1］用式（1）计算预应力混凝土桥梁的自振频率，即认为预压力的效应等同于外轴力的效应.随即有3篇论文对Saiidi的论文进行了讨论.Dallasta［2］指出Saiidi的计算方法不正确，认为预压力的效应可以忽略.Deak［3］指出预压力不减少梁的自振频率，不过没有给出任何理论分析.Jain［4］认为，预应力筋，作为结构系统的一个组成部分，产生的预压力不能被处理为外轴力，预压力不产生压缩软化效应，不影响梁的自振频率.Jaiswal［5］用有限元法计算了预应力梁的第1自振频率，指出预压力对梁的第1自振频率的影响取决于预应力筋与梁的粘结与否.对于有粘结筋，预压力对梁第1自振频率无明显影响.对于无粘结筋，预压力和偏心距对梁第1自振频率有明显影响.不过，Jaiswal［5］的结论只是基于有限元的计算结果，没有进行解析分析.Kanaka［6］把预压力当作外轴力，用Rayleigh-Ritz法分析，指出预压力降低了梁的低阶自振频率.Chan［7］指出，由于压缩软化效应，随着预压力的增加，预应力梁的自振频率降低.Dallasta［8］应用梁的小位移运动学关系，分析了无粘结预应力梁，给出梁的振动微分方程，并指出随着预压力的增加，梁的自振频率降低.Kerr［9］对预应力梁的动力响应作了试验和理论分析，发现：当预应力筋布置在梁轴线上，预应力筋的预应力大小不影响梁的动力响应.不过，Kerr只采用线性理论模型计算预应力梁的动力响应，且预应力筋与梁轴线重合.Wang［10］考虑了预压力产生的附加势能，得出结论：预压力降低梁的低阶自振频率.Hamed［11］基于哈密尔顿原理，应用虚功的变分方程，严格推导出预应力梁的运动方程，该运动方程适用于各种形状的预应力筋.Hamed［11］严格证明了有粘结梁或无粘结梁中预压力的大小不影响预应力梁的自振频率.

除了体内有粘结和无粘结两种预应力体系，还有体外预应力体系.当无粘结预应力梁和体外预应力梁具有相同的预应力筋线形，与无粘结筋相比较，体外筋存在偏心距损失，体外筋的应力增量小于无粘结筋的应力增量，这导致了体外预应力梁的刚度小于无粘结预应力梁的刚度，自然地，体外预应力梁的自振频率应低于无粘结预应力梁的频率.这样看来，Hamed［11］的结论不适用于体外预应力梁.不过，文献［12-13］在体外预应力梁的动力微分方程中，把体外筋预压力对自振频率的效应等同于外轴力的效应.体外预应力梁中的偏心距损失与转向座的数量和位置相关，随着转向座数量的增加，体外筋趋向于无粘结筋.根据Hamed［11］的结论，体外筋预压力对自振频率的效应降低，并趋向于零，所以体外筋预压力的效应等同于外轴力的效应，这一观点有待进一步商榷.文献［14］用能量法分析了体外预应力梁动力特性，也指出：体外预压力能减小梁的自振频率，而体内预压力（有粘结或无粘结）对梁的自振频率没有影响.不过从文献［14］式（10）可以看出：对于简单的直线型体外筋，ψ＝（iπ）2／4l，与转向座的数量和位置无关，所以这一观点并没有得到解析解的支持.一些实验表明［15］：随着体外筋预压力的增加，梁中的微裂缝闭合，体外预应力梁的刚度和自振频率反而增加，于解析解式（1）的结论完全相反.同时，体外预压力的效应并不显著，通过实验研究体外预压力的效应不易得出一致的结论.因此，体外预压力效应的理论分析就显得尤为重要.据笔者所知，尚未有文献对这一效应进行合适的理论分析.本文精细地考虑了体外筋变形中的二阶项，引入体外预压力压缩软化效应的影响系数.这一影响系数表明：转向座数量从零增加到较多的数目，体外筋接近于无粘结筋，体外预压力的效应从外轴力的效应减少至接近于零，这符合Hamed［11］的结论，即无粘结筋的预压力不产生压缩软化效应.

1 考虑二阶效应的能量法

本文采用能量法［16］.假设1：图1体外预应力简支梁第i振型的振动方程yi＝Aisin(iπx／l)sin（ωit+φi），i＝1，2，3…，与普通简支梁的解析解相同.假设2：施加体外预应力后，梁为直线.假设3：略去梁的轴向变形，略去体外筋的质量.

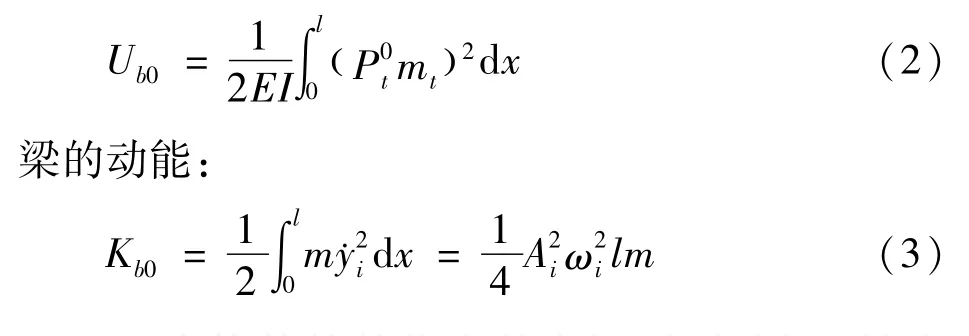
mt为体外筋单位力的弯矩图，如图2所示，为体外筋初始预拉力的弯矩，mij＝cosθiej，体外筋的角度θi和偏心距ej，如图1所示.体外筋的应变能：

EtAt，lt分别为体外筋的抗拉刚度、长度.

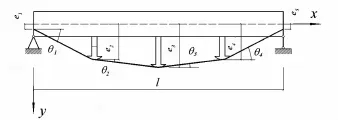
图1 体外预应力简支梁Fig.1 Externally prestressed simply supported beam

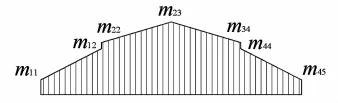
图2 体外筋单位力的弯矩图Fig.2 Bendingmoment diagram of the beam subjected to the unit force of external tendon

当yi为最大时，或时，梁的弯矩：Mb1＝梁的应变能：

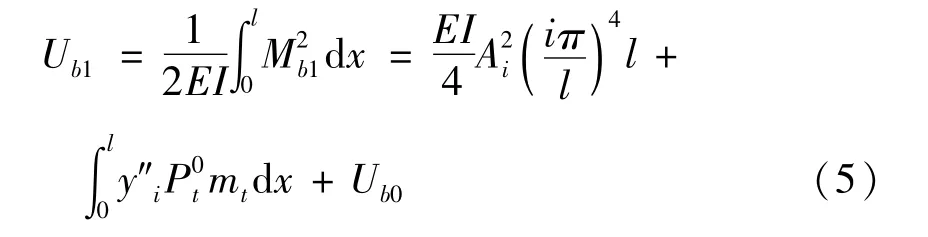
在计算体外筋的变形前，先分析图3中线段OA的变形.线段OA在x和y轴方向上的变形为δx和δy.考虑二阶微分，线段OA的变形为：

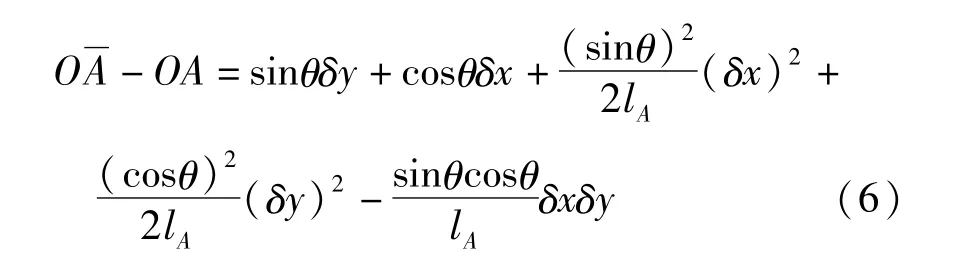
θ和lA为线段OA的夹角和长度.在分析体外筋预压力的压缩软化效应中，二阶项是必不可少的.文献［14］不考虑这个二阶项，所以本文的分析方法比文献［14］更深入、更精确.在体外筋和梁之间有n个接触点，第1和最后接触点在梁的两端，其他接触点位于转向座.体外筋的第j线段，振动前，第j和（j+1）接触点的坐标为（xj，ej）和（xj+1，ej+1）.考虑梁轴线弯曲产生的x轴的投影缩短，当i＝0时，第j和（j+1）接触点的坐标

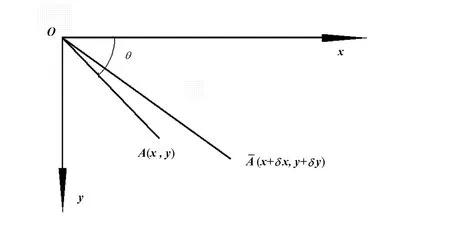
图3 线段OA的变形Fig.3 Deformation of Line OA

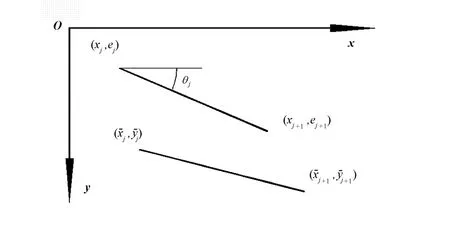
图4 体外筋线段的变形Fig.4 Deformation of external tendon segment

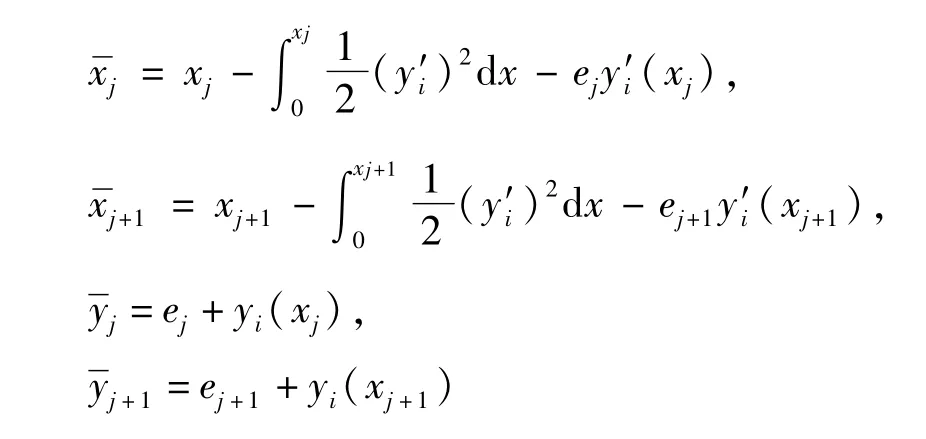
第j线段x和y轴方向上的变形δxj和δyj：

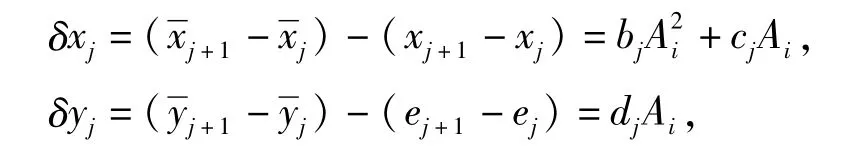
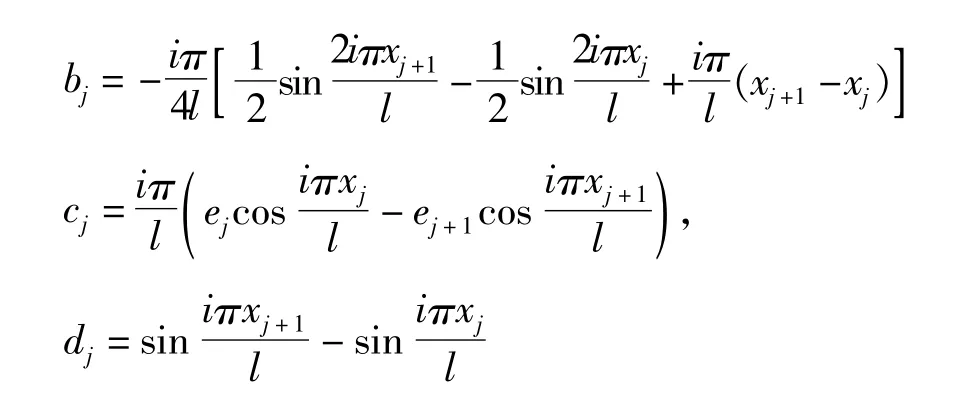
把δxj和δyj代入式（6），略去含项的高阶无穷小（振幅Ai可以是无穷小量），得出体外筋第j线段的变形：

体外预压力的影响系数Cpi＝-4lζi／（iπ）2.可以看出：体外预压力影响梁的自振频率，其影响系数Cpi取决于转向座的数量和位置.表1为Cpi与接触点数量n的关系.表1中，转向座沿梁长度等距离分布，对称的体外筋线形，梁长l＝16m，两端处的偏心距e1＝en＝0.2m.对于抛物线体外筋，转向座处的接触点均位于抛物线上（图1），抛物线在跨中的最大偏心距为1m.从表1可以看出：当只有2个接触点，即无转向座时，体外筋偏心距损失为最大，此时不分直线形或抛物线形，影响系数均为1.比较式（1）和（12）可知，体外预压力的压缩软化效应与外轴力的效应相同.随着接触点数量的增加，偏心距损失减小，影响系数降低.总体而言，随着振型阶数的增加，振型中每半波正弦曲线内的接触点数量减少，导致影响系数增大.如同在第1振型中，接触点数量减少，影响系数增大.抛物线形和直线形的影响系数相近，影响系数主要取决于接触点数量n.当n从2增加到比较大的数值时，体外筋接近于无粘结筋，影响系数从1降低至接近于0.这符合Hamed［11］的结论，即无粘结筋的预压力不产生压缩软化效应，不影响梁的自振频率.

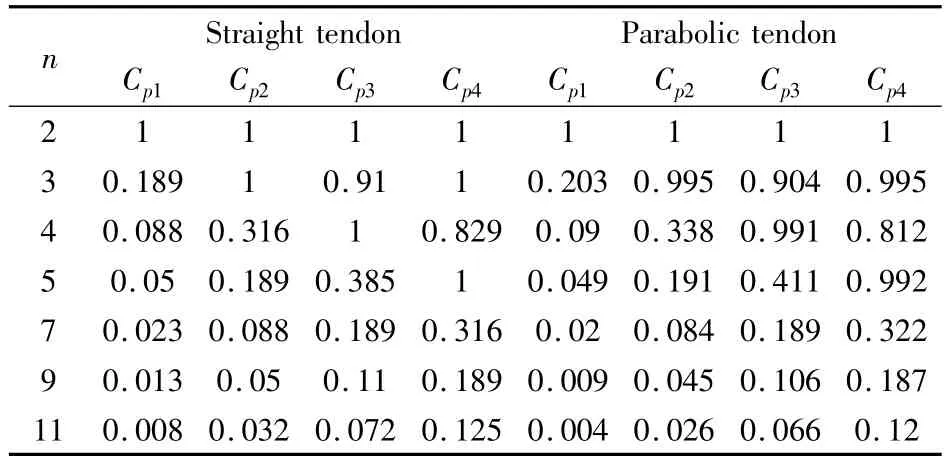
表1 影响系数Cpi与接触点数量n之间的关系Table 1 Relationship between the influence coefficientCpiand the number of contact pointsn

2 算例分析

图1体外预应力简支梁的单位长度质量m＝6t／m，梁长l＝16m，横截面为矩形，高0.8m，宽0.4m，弹性模量E＝32.5GPa，转向座沿梁长度等距离分布；体外筋弹性模量Et＝200GPa，有效预应力对称体外筋线形，e1＝0.2m.表2列出体外预应力梁的第1、2、3阶自振频率，梁1～8中有两种体外筋面积At＝1668，2502mm2，两种偏心距e2＝0.8，1.1m和两种线形，梁1，3，5，7的梯形线形（2个转向座，偏心距为e2），梁2，4，6，8的抛物线形（e2＜e3，3个转向座，见图1）.ω①为本文式（12）的计算结果，ω②为文献［14］式（10）的计算结果.表3为无预压力梁的第1、2、3阶自振频率，其中0号梁无体外筋.比较表2和表3，可以看出：

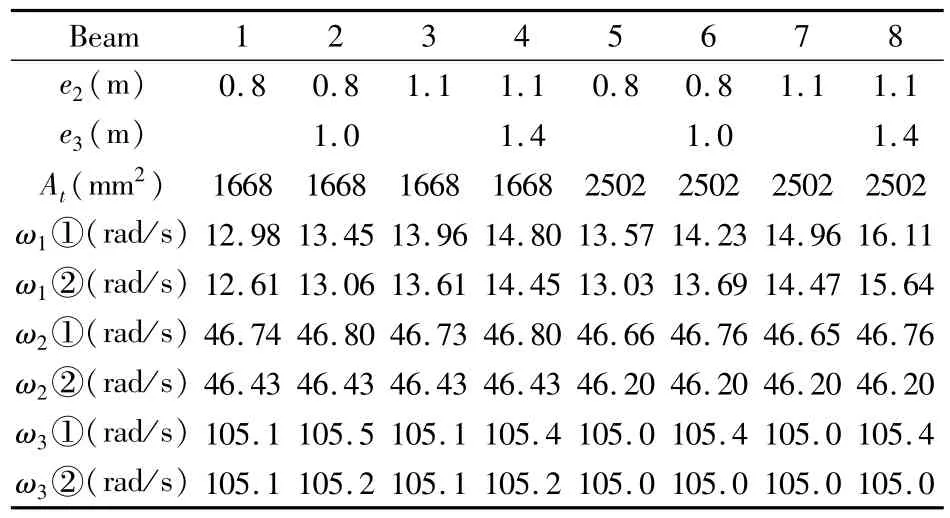
表2 体外预应力梁的第1、2、3阶自振频率Table 2 The 1st，2ndand 3rdnatural frequencies of externally prestressed beams

表3 无预压力梁的第1、2、3阶自振频率Table 3 The 1st，2ndand 3rdnatural frequenciesof beams without prestress force

3 结论

外轴力产生压缩软化效应，降低梁的自振频率.体内有粘结或无粘结筋的预压力不产生压缩软化效应［11］，不影响自振频率.本文推导了考虑二阶效应的体外预应力梁的自振频率公式，首次阐明了体外预压力对梁自振频率的效应既不同于外轴力的效应，也不同于体内有粘结或无粘结筋预压力的零效应，而是介于两者之间.研究结果表明：

1）体外预压力的压缩软化效应，即自振频率的影响系数，主要取决于转向座的数量.无转向座时，体外筋偏心距损失为最大，影响系数为1，体外预压力的效应与外轴力的效应相同.随着转向座数量的增加，偏心距损失减小，体外筋接近于无粘结筋，影响系数降低至接近于0，体外预压力几乎不产生压缩软化效应，几乎不影响梁的自振频率.这与Hamed［11］的结论相符，即有粘结或无粘结筋的预压力不影响自振频率.

2）对于实际工程中的梁，当转向座的数量≥2时，由于影响系数显著地小于1.同时预压力也不大，体外预压力对自振频率的影响很小，可以忽略.

3）体外筋显著地影响梁的ω1，体外筋的面积和偏心距的增加，体外筋对梁的刚度贡献随之增加，ω1自然也增加了.不过，体外筋对其他阶自振频率的影响很小，可以忽略.

1 Saiidi M，Douglas B，Feng S.Prestress force effect on vibration frequency of concrete bridge.ASCE Journal of Structural Engineering，1994，120（7）：2233～2241

2 Dallasta A，Dezi L.Prestress force effect on vibration frequency of concrete bridge-discussion.ASCE Journal of Structural Engineering，1996，122（4）：458～458

3 Deak G.Prestress force effect on vibration frequency of concrete bridge-discussion.ASCE Journal of Structural Engineering1996，122（4）：458～459

4 Jain SK，Goel SC.Prestress force effect on vibration frequency of concrete bridge-discussion.ASCE Journal of Structural Engineering，1996，122（4）：459～460.

5 Jaiswal O R.Effect of Prestressing on the first flexural natural frequency of beams.Structural Engineering and Mechanics，2008，28（5）：515～524

6 Kanaka K，Venkateswara G.Free vibration behavior of Prestressed beams.ASCE Journal of Structural Engineering，1986，121（7）：433～437

7 Chan TH T，Yung TH.A theoretical study of force identification using prestressed concrete bridges.Engineering Structures，2000，22（11）：1529～1537

8 Dallasta A，LeoniG.Vibration of beams prestressed by internal frictionless cables.Journal of Sound and Vibration，1999，222（1）：1～18

9 Kerr A D.On the dynamic response of a prestressed beam.Journal of Sound and Vibration，1976，49（4）：569～573

10 Wang Z C，Ren W X.Dynamic analysis of prestressed concrete box-girder bridges by using the beam segment finite element method.International Journal of Structural Stability and Dynamics，2011，11（2）：379～399

11 Hamed O，Frostig Y.Natural frequencies of bonded and unbonded prestressed beams-prestress force effects.Journal of Sound and Vibration，2006，295（1-2）：28～39

12 Miyamoto A，Tei K，Nakamura H，Bull JW.Behavior of prestressed beam strengthened with external tendons.ASCE Journal of Structural Engineering，2000，126（9）：1033～1044

13 熊学玉，王寿生.体外预应力梁振动特性的分析与研究.地震工程与工程振动，2005，25（2）：55～61（Xiong X Y，Wang SS.Analysis and research of externally prestressed beam vibration behavior.Earthquake Engineering and Engineering Vibration，2005，25（2）：55～61（in Chinese））

14 方德平，王全凤.体外预应力梁动力特性的能量法分析.振动与冲击，2012，31（1）：177～181（Fang D P，Wang Q F.Analysis of dynamic behavior of externally prestressed beam by energymethod.Journal of Vibration and Shock，2012，31（1）：177～181（in Chinese））

15 张耀庭，汪霞利，李瑞鸽.全预应力梁振动频率的理论分析与试验研究.工程力学，2007，24（8）：116～120（Zhang Y T，Wang X L，Li R G.Experimental and theoretical research on vibration Frequency of full-prestressed concrete beam.Engineering Mechanics，2007，24（8）：116～120（in Chinese））

16甘亚南，石飞停.宽翼T形梁桥动力学理论与特性分析.动力学与控制学报，2013，11（4）：350～356（Gan Y N，Shi F T.Analysis on dynamic theory and characteristic of thin-wall T-beamswith wide flanges.Journal of Dynamics and Control，2013，11（4）：350～356（in Chinese） ）

SECOND ORDER EFFECT OF EXTERNAL TENDON COMPRESSION ON DYNAM IC BEHAVIOR OF SIMPLY SUPPORTED BEAM BY ENERGY METHOD*

Fang Deping†Zhong Mingjing
（College of Civil Engineering，Huaqiao University，Xiamen361021，China）

Precisely considering the second order term in external tendon deformation，the natural frequency of externally prestressed beam is derived by energy method.It illustrates the effect of external tendon compression on beam natural frequency.The calculation results also show that the influence coefficient stating the softening effect of the external tendon compression mainly depends on the number of deviators.Without deviator，the eccentricity loss ismaximum，the influence coefficient is 1，and the effect of external tendon compression is the same as thatof the external axial force.As the number of deviators increases，the eccentricity loss decreases，the external tendon is close to the unbonded tendon，and the influence coefficient decreases to near zero，which is close to nought effectof unbonded tendon compression.For the beam with two ormore deviators，due to the influence coefficient significantly less than 1，the external tendon compression softening effect is negligible.With the increase of the eccentricity and tendon area，the first natural frequency grows up，but the effect of the external tendon on other frequencies is negligible.

external prestress， simply supported beam， natural frequency， energy method， dynamic analysis， second order effect

10.6052／1672-6553-2015-73

2015-7-2收到第1稿，2015-9-1收到修改稿.

*国家自然科学基金资助项目（51578253，51578255）

†通讯作者E-mail：fdp＠hqu.edu.cn

Received 2 July 2015，revised 1 September 2015.

*The project Supported by the National Natural Science Foundation of China（51578253，51578255）

†Corresponding author E-mail：fdp＠hqu.edu.cn