微型压电层合板结构的振动特性研究*

张霄峙 陈丽华张伟

（北京工业大学机械工程与应用电子技术学院，机械结构非线性振动与强度北京市重点实验室，北京 100124）

微型压电层合板结构的振动特性研究*

张霄峙 陈丽华†张伟

（北京工业大学机械工程与应用电子技术学院，机械结构非线性振动与强度北京市重点实验室，北京 100124）

从经典薄板理论出发，基于应变梯度理论，综合考虑尺寸效应和压电效应的影响，利用哈密顿原理建立了微型压电层合板结构的动力学模型及其边界条件.在选取符合其边界条件的模态函数后，利用Ritz法分别研究四边简支和悬臂条件下的微型压电层合板的振动特性，求解了前五阶固有频率并绘制了3D模态图.分析了微尺度带来的尺寸效应对于固有频率的影响，最后研究了外加电压对于系统固有频率的影响.

应变梯度理论， Ritz法， 微型压电层合板， 固有频率， 振型

引言

近年来，微机电系统（MEMS）领域发展迅猛，整个业界都呈现出小型化、微型化、复杂化的趋势［1-2］.这类新型设备具有一个普遍特点：其结构及其变形所涉及的长度尺寸都很小，和其材料特征长度处于一个数量级.而大量实验表明，微结构所带来的尺寸效应会使结构与材料的力学特性发生传统连续介质力学不能解释的显著变化.例如，Fleck［3］等利用微米量级的不同直径的细铜丝，进行了著名的扭转实验.当细铜丝的直径由170μm减小到12μm，无量纲化的抗扭刚度增加了3倍.Stolken和Evans［4］利用镍薄梁进行弯曲实验，观察到当梁的厚度从50μm减小到12.5μm时，无量纲化的抗弯刚度也显著增加.更能说明材料在微米尺度下具有尺度效应的是微米及亚微米压痕实验，压入深度小于50μm时，压痕硬度表现出非常强烈的尺寸效应.对于金属材料，所测的材料硬度值随着压入深度的减小可达到传统硬度值的2倍甚至3倍左右.

为了解释这种尺寸效应，从尝试引入偶应力的Cosserat兄弟开始.Toupin［5］，Yang［6］等学者均各自提出了不同的偶应力理论.1964年，Mindlin［7］提出了弹性全应变梯度理论，其理论认为连续介质中每一个物质点从微观角度可以看作一个胞元，这个胞元不仅跟随连续介质作宏观运动和变形，而且自身还有微观位移和微观变形.因此，应变能密度函数依赖于宏观介质的应变，宏观介质应变和微粒应变之间的相对应变，以及微观变形梯度.

与此同时，国内外学者利用应变梯度理论对各种微型结构进行了研究.2008年，Papargyri-Beskou和Beskos［8］运用应变梯度理论分析了弹性梯度弯曲Kinchhoff微型板结构的静态变形、稳定性和线性固有频率.2009年，Lazopoulos［9］基于Aifantis提出的基于应变梯度的应变能密度方程，和表面能量带来的附加值，建立了另一种Kinchhoff微型板结构的模型.2011年，Reddy［10］研究了微结构Euler-Bernoulli和Timoshenko功能梯度材料梁的非线性振动问题.

数值模拟中，当自由振动时，他们建立的模型相比经典理论模型有更低的固有频率.2012年，Ramezani［11］提出了基于标准弹性应变梯度理论的一阶剪切变形微型板结构模型，主要研究了结构的静态弯曲和线性固有频率，指出所谓的尺度效应对于提升微型板结构刚度的重要作用.2012年和2013年，Ramezani＆Rajabi［12-13］利用应变梯度理论研究了微型梁结构的非线性问题，并发现非线性是提升结构固有频率的主要原因.但在某些特殊的长厚比情况下，尺度效应也有明显提升固有频率的效果.

同时，微机电系统（MEMS）在与片上系统、无线通信和低功耗嵌入式技术不断交流和融合中，孕育出无线传感器网络的概念.随着信息技术的不断发展，对无线传感器的需求迅速增长，压电结构得到了越来越广泛的应用，尤其是压电俘能器领域.目前对微型压电结构的研究大多没有考虑尺寸效应的影响［14-19］.仅有的考虑尺寸效应的文献［20］也只是对梁和圆板结构进行了研究.

本文从经典薄板理论出发，基于应变梯度理论，综合考虑尺寸效应和压电效应的耦合，利用哈密顿原理建立了微型压电层合板结构的动力学模型.分别针对四边简支和悬臂两种边界条件，利用Ritz法求解了微型压电层合板的固有频率及模态函数，研究了其振动特性.

1 应变能表达式

对于微型结构，考虑尺寸效应，基于应变能梯度理论，总的应变能密度函数是应变、应力及应变梯度、高阶应力的函数.所以系统总的应变能密度函数由两部分组成：一部分为基于连续介质力学得到的宏观应变能；另一部分是基于应变梯度理论得到的微观应变能.

图1 结构示意图Fig.1 Structuremodel

微型压电层合板结构设计如图1所示.结构

由一层材质为MEMS常见材料硅的基层，另一层为压电材料层组成，层间无相对位移，每层的厚度都远小于结构的长和宽.基于经典薄板理论由此可设板内任一点的位移为：

w为该点垂直于中性面的挠度，x和y分别表示面内对应的坐标.不考虑剪切变形的影响，可得出板内任一点应变为：

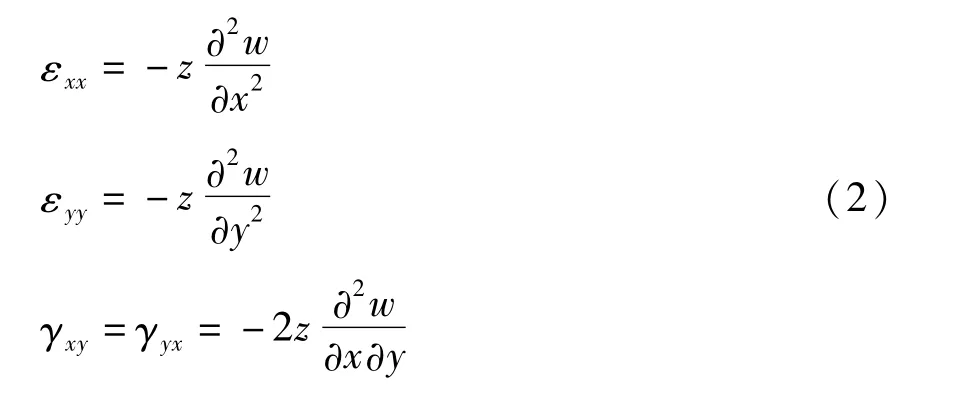
为考虑压电耦合效应的影响，分别针对基层和压电材料层，分别计算板的应力.结果可表示为：

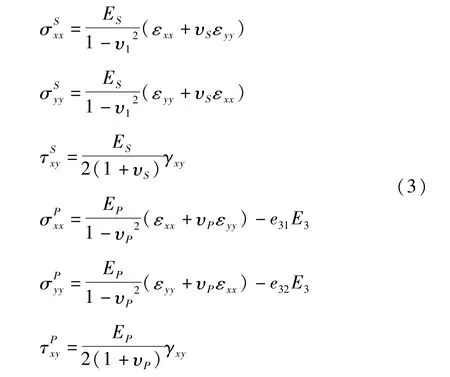
上标S代表基层，P代表压电层，Eξ及υξ分别为杨氏模量和莫松比，e31、e32为压电常数，E3为电场强度，E3＝V／hP，hP为压电层的厚度，V为电压.

基于连续介质力学理论，系统宏观变形的应变能可写为：

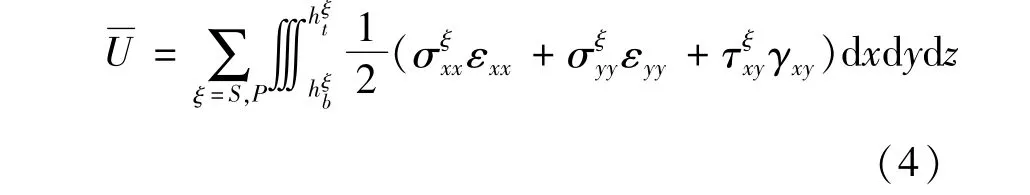
本文采用Ⅱ型应变梯度表达式：

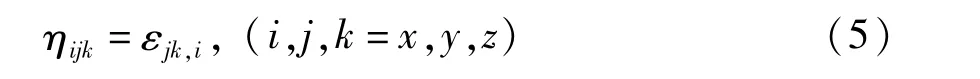
由（2）、（5）式，得ηijk各项表达式如下

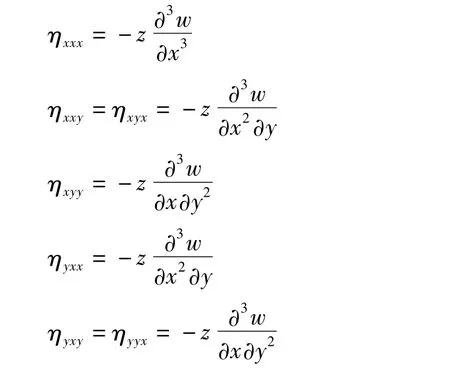
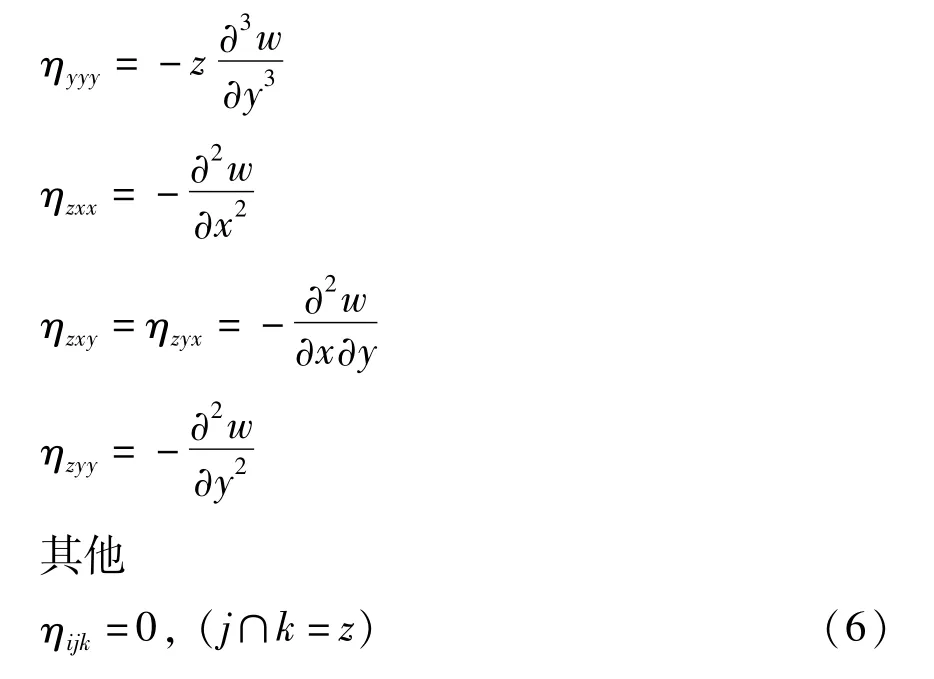
基层和压电层微观部分应变能密度表达式可写为：

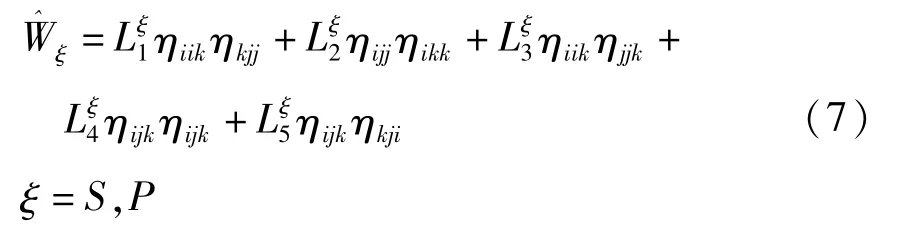
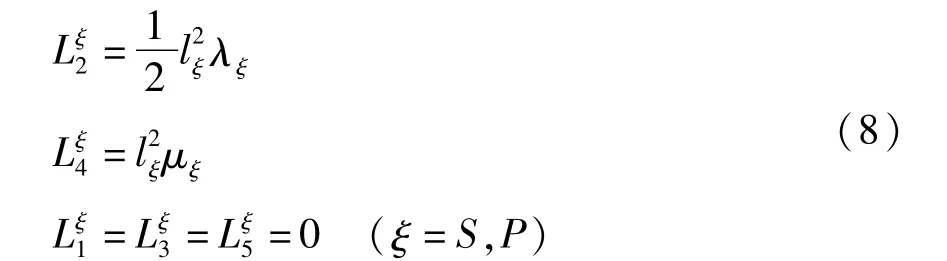
式中lξ为材料內凛长度系数，取决于具体材料，λξ和μξ为常见的拉梅常数，表达式为：

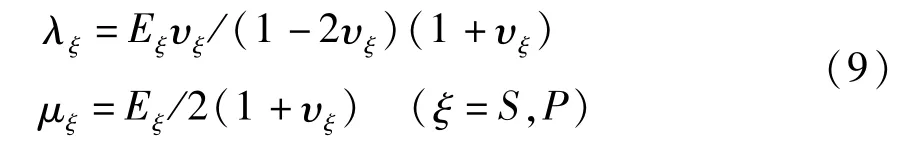
由微观变形应变能密度表达式（7），高阶应力张量χ可由下式求得：

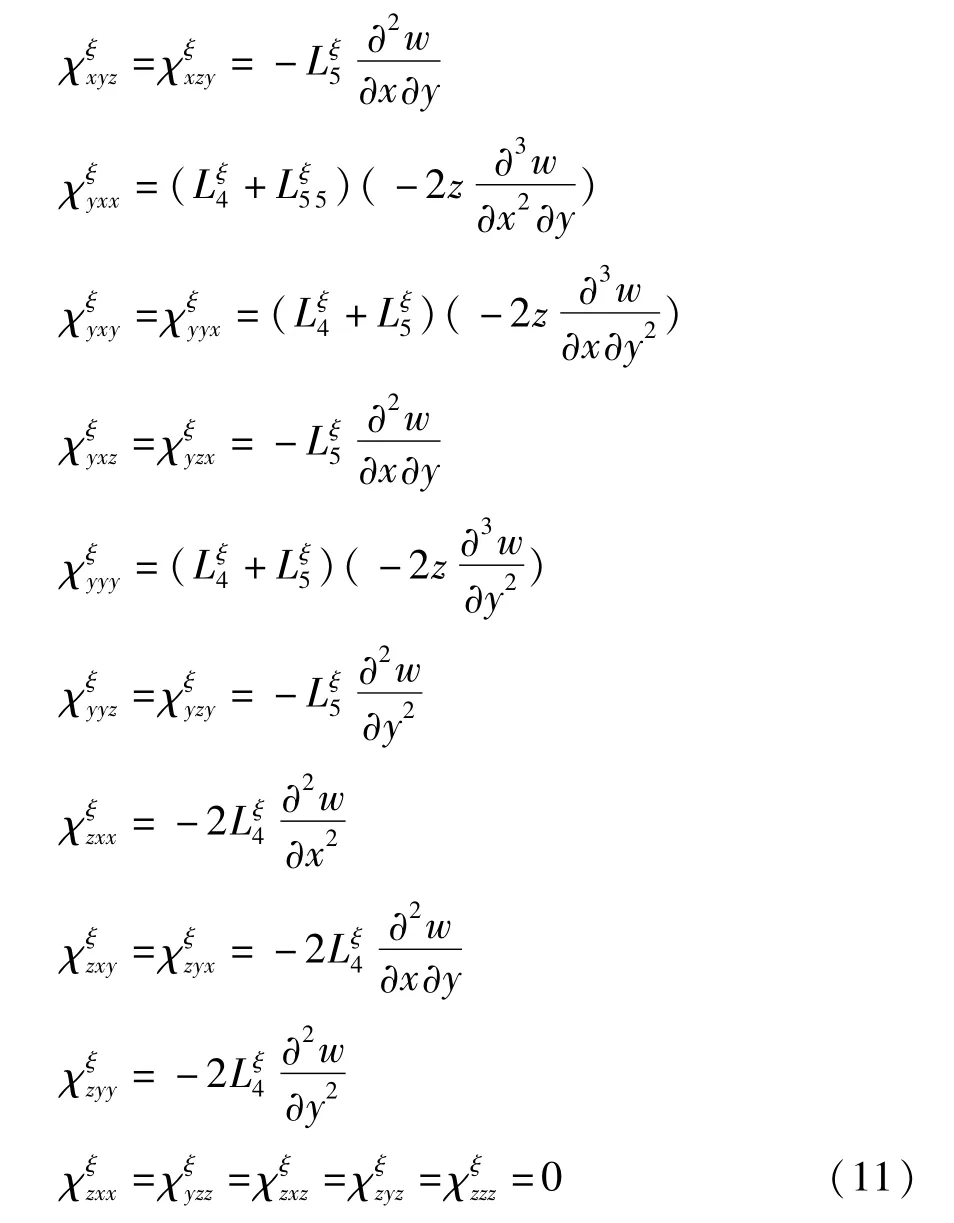
公式（10）中δij为克罗内克函数.

基于应变梯度理论，微型压电层合板结构微观变形部分的应变能为：

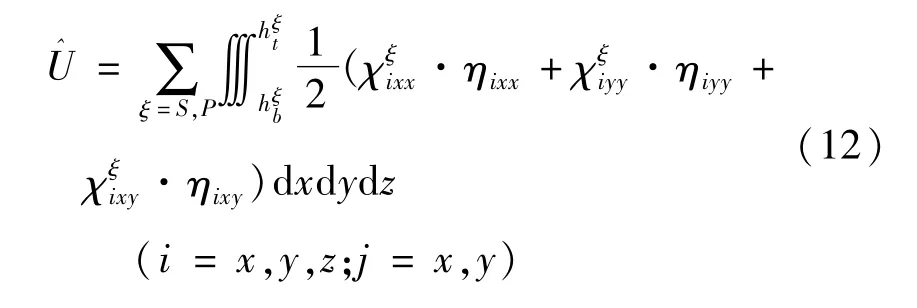
2 动力学模型

本节将利用哈密顿原理来得到系统的动力学模型及边界条件.

哈密顿原理的表达式为：

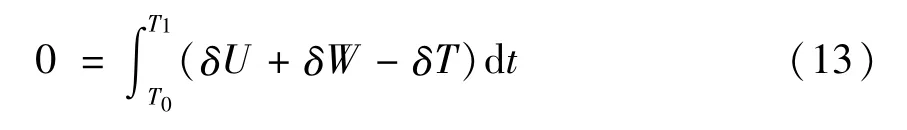
其中微型压电层合板结构的势能U由两部分构成：

系统的动能由各层的动能相加得到：

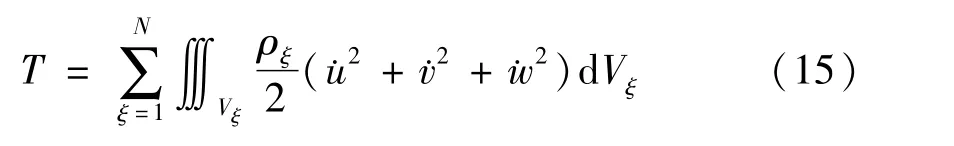
式中ρξ各层材料的密度.

本文研究自由振动的情况，无外力做功，故W＝0.

将（14）式、（15）式代入哈密顿原理（13）式并计算后得到动力学方程：

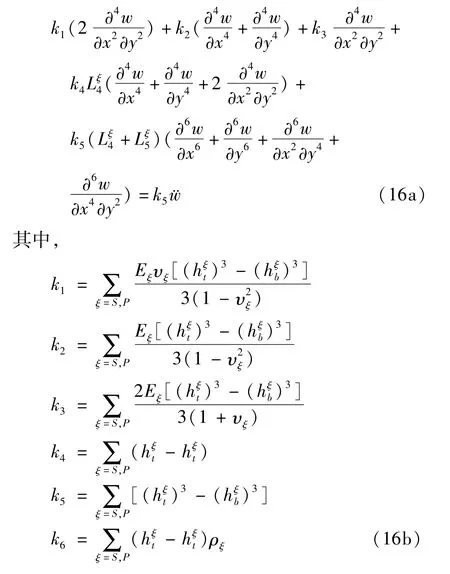
3 边界条件

在得到动力学方程的同时，微型压电层合板结构的边界条件归纳为如下几种情况.

3.1 支撑情况为四边简支时

（1）在x＝0（a边）：

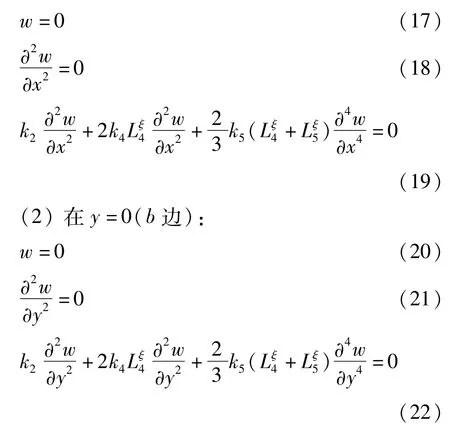
3.2 支撑情况为悬臂时

（1）在固定边x＝0：

（2）在自由边x＝a：

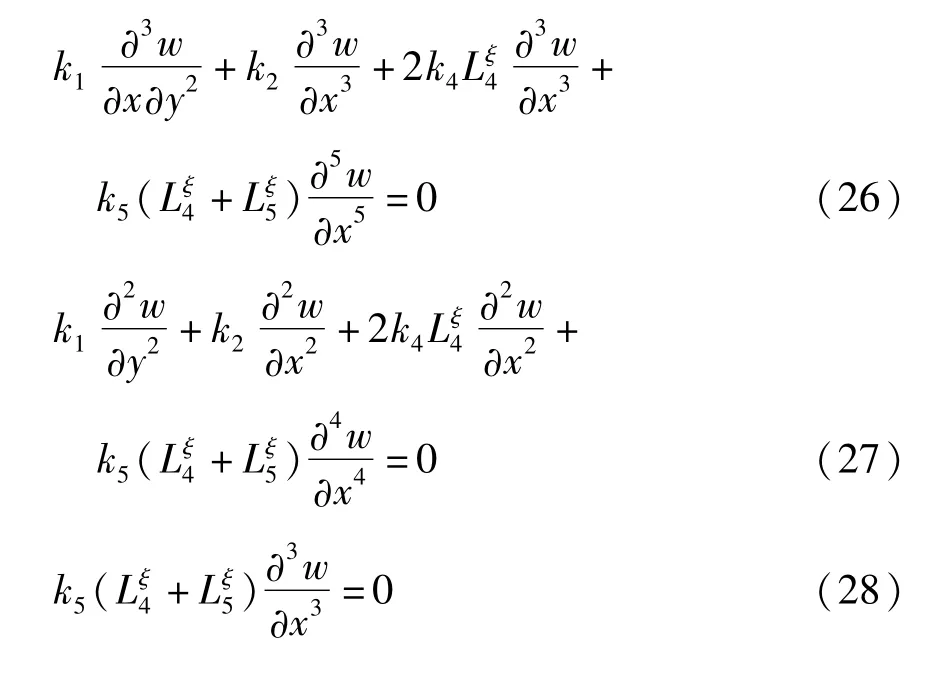
（3）自由边y＝0、y＝b：

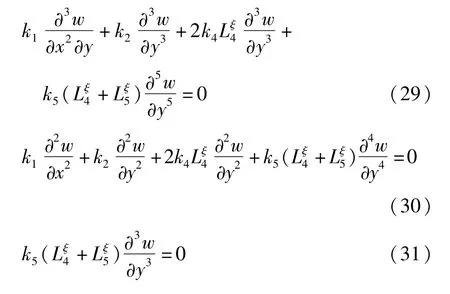
4 求解固有频率和模态函数图

本节采用Ritz法求解微型压电层合板结构的固有频率和模态.Ritz法基于能量变分原理，将泛函极值问题转化为多元函数极值问题来求解.

首先将板自由振动解的形式设为：

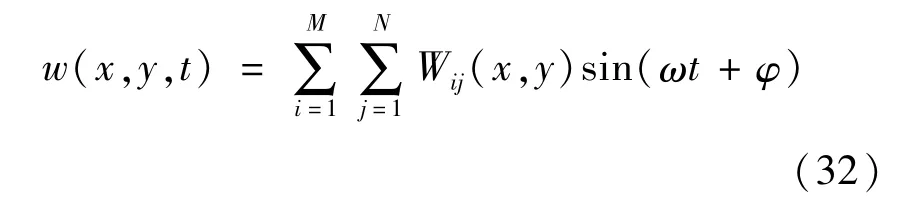
（1）对于简支边界条件，本文选取的模态函数为：

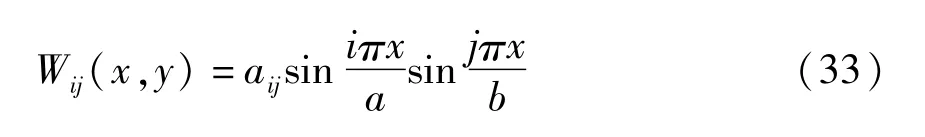
（2）对于悬臂板，选取梁函数为试函数，悬臂板模态函数的表达式为：

在自由-自由方向，试函数可以选择满足边界条件的梁函数：在固定-自由方向，相应的梁函数为：

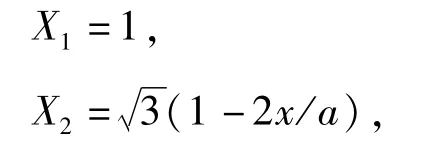
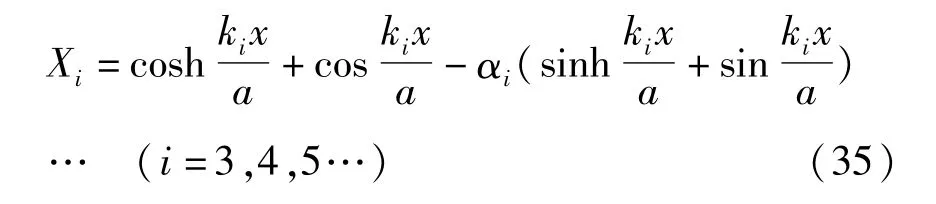
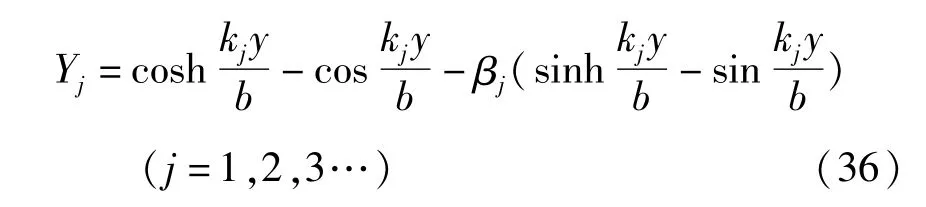
ki，kj，αi，βj的表达式见参考文献［21］.

将（32）式代入到系统势能、动能的表达式中，再代入哈密顿原理后对时间t进行积分，可得到：

其中aij为待定系数，也相当于独立的广义坐标.于是，变分式（37）式可以简化为多元函数的极值条件：Umax-Tmax对待定系数aij的偏导数为零，即

经过计算，可得关于aij的线性代数方程式.令方程组的系数行列式等于零即可得到固有频率ω.将求出的ω值代入线性方程组式（38）中求出待定系数，便得到各阶固有频率相对应的模态函数.

利用前文所述的求解固有频率和模态函数的方法，本节代入具体微型压电层合板结构的几何参数和材料参数进行计算.材料参数如表1.

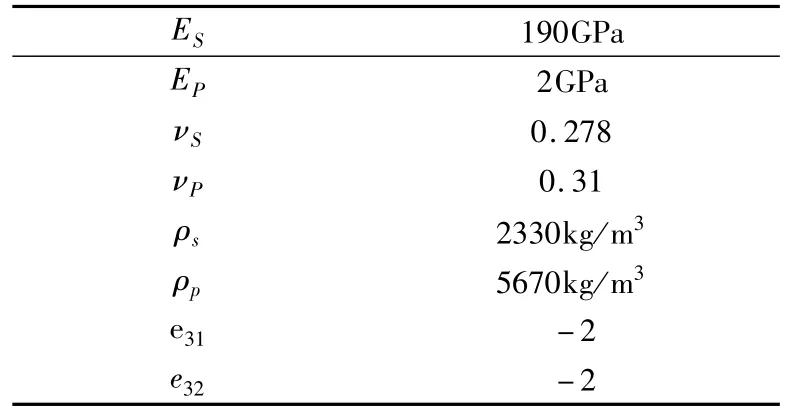
表1 材料参数Table 1 Material parameters

为了研究尺寸效应对微型结构固有频率的影响，下面分别选取几组不同的几何参数进行计算：

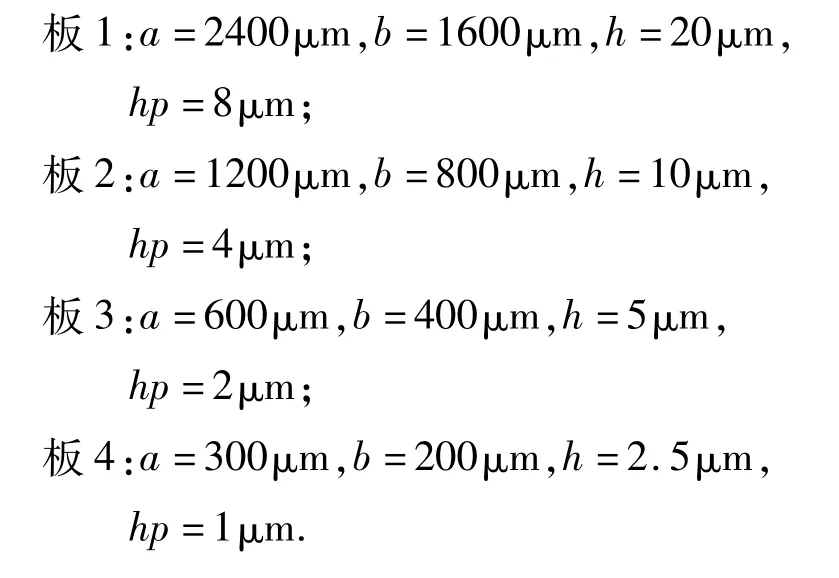
本文算例中采用的板都为3层结构，中间基层的厚度为h，上下压电层的厚度为hp.

4.1 支撑情况为四边简支时

选择材料內凛长度为1μm，电压V＝0.利用Ritz法，基于Maple软件，求得的微型压电四边简支压电层合板结构的固有频率结果如表2.

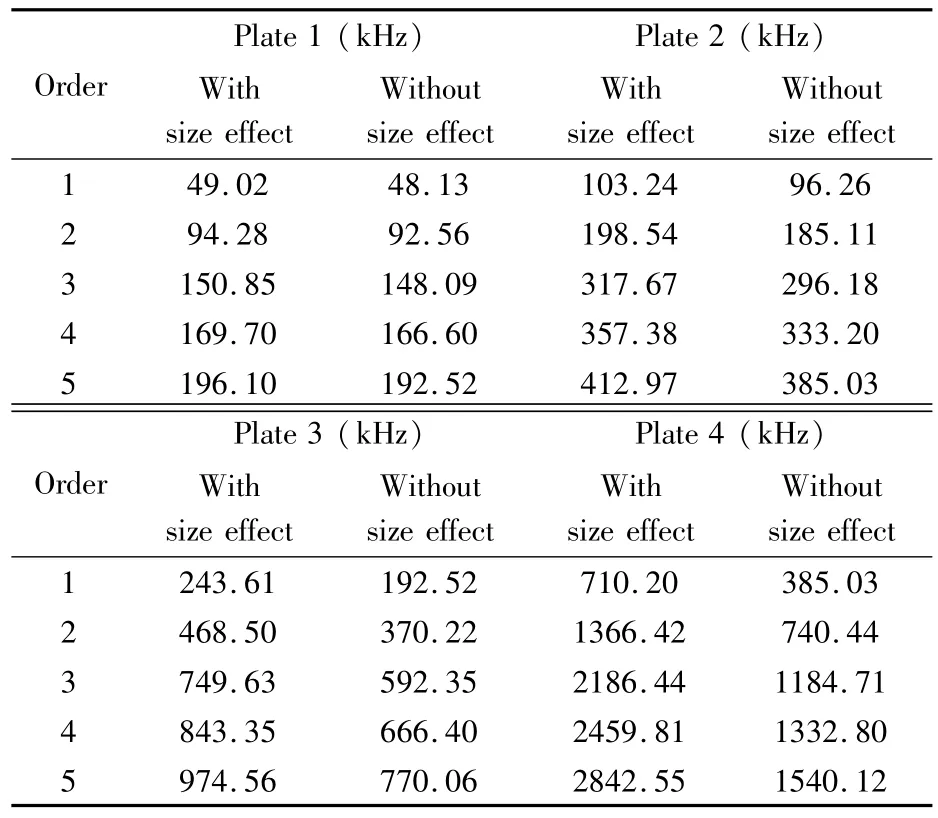
表2 固有频率计算结果Table 2 Numerical results of natural frequencies

考虑尺寸效应的影响应用梯度理论，本文得到的前五阶固有频率值较不考虑尺寸效应时的值都有所提高.图2给出了每一阶固有频率提高的百分比.

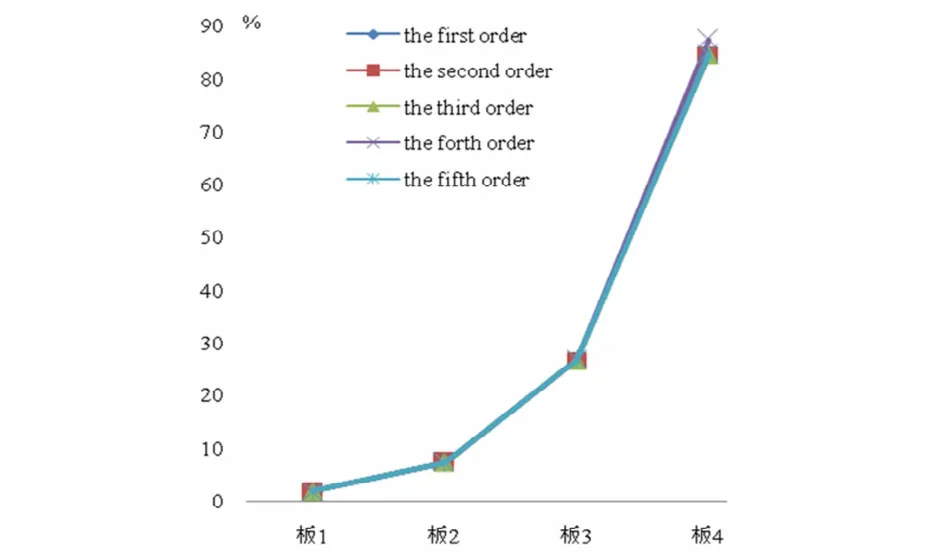
图2 考虑尺寸效应后各阶固有频率提升百分比Fig.2 Improvement percentage of natural frequencies considering the size effect

在得到各阶固有频率后，通过Maple软件计算并绘制了振型函数图，如图3所示.

通过对固有频率的计算，发现由微结构带来的尺度效应对结构刚度有提升效果.且该效果随着结构尺寸的减小愈发显著.由此表明在研究微型结构的力学特性时，不可忽略尺寸效应的影响，需要利用微观力学理论进行分析.

为研究材料內凛长度l对固有频率的影响趋势，选取板3为研究对象，考察不同材料內凛长度l和板厚度的比值下的固有频率变化情况，结果如下，单位kHz.

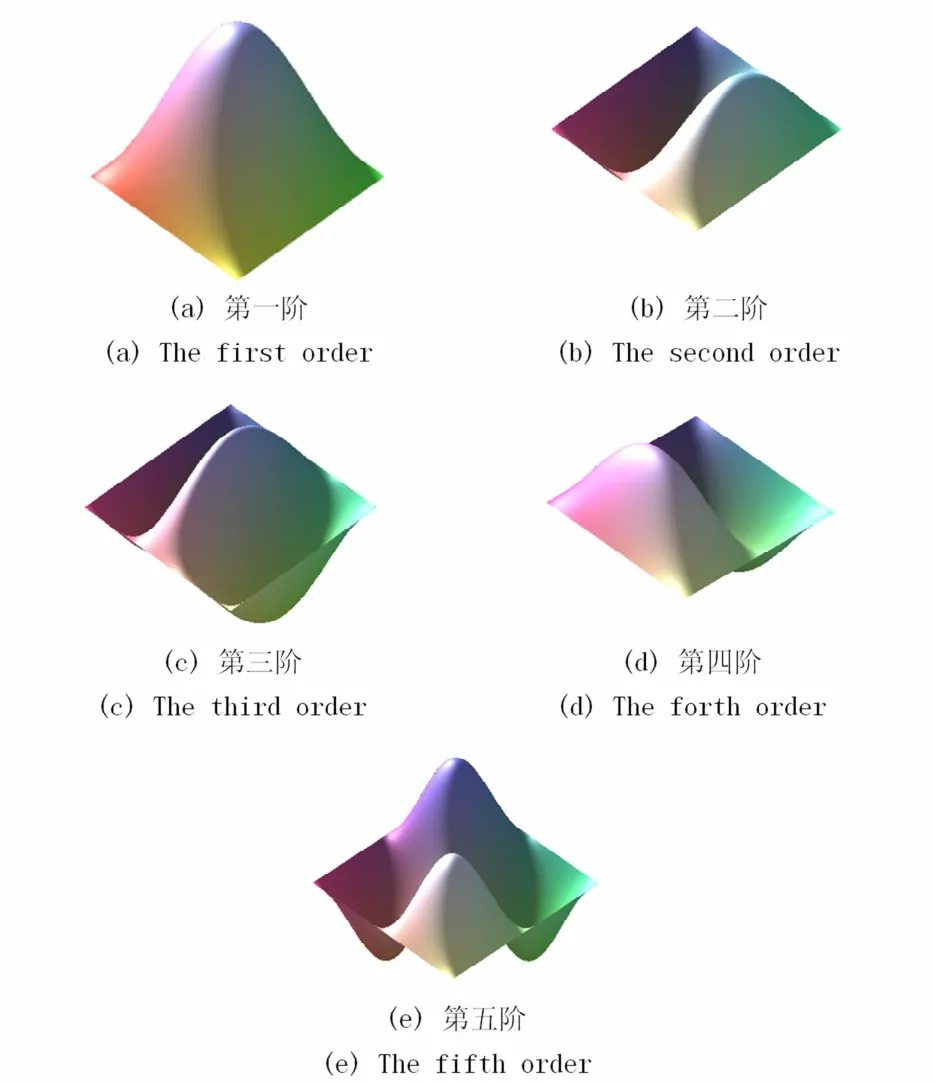
图3 前五阶函数图Fig.3 Mode shapes of the first five orders

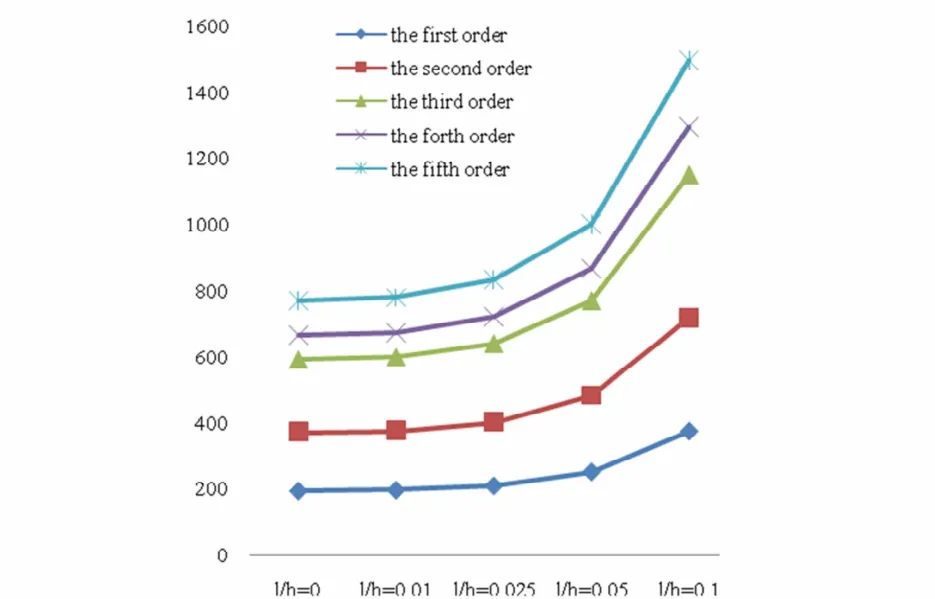
图4 各阶固有频率随l／h变化图Fig.4 Development of natural frequencies with differentl／h

通过计算发现随着材料內凛长度与板厚度的比值的增大，固有频率呈现出上升的趋势，该趋势表明尺寸效应的影响愈发明显.

4.2 支撑情况为悬臂时

选择材料內凛长度为1μm，电压V＝0，利用Ritz法，基于Maple软件，求得的微型压电悬臂压电层合板结构的固有频率结果如表3.

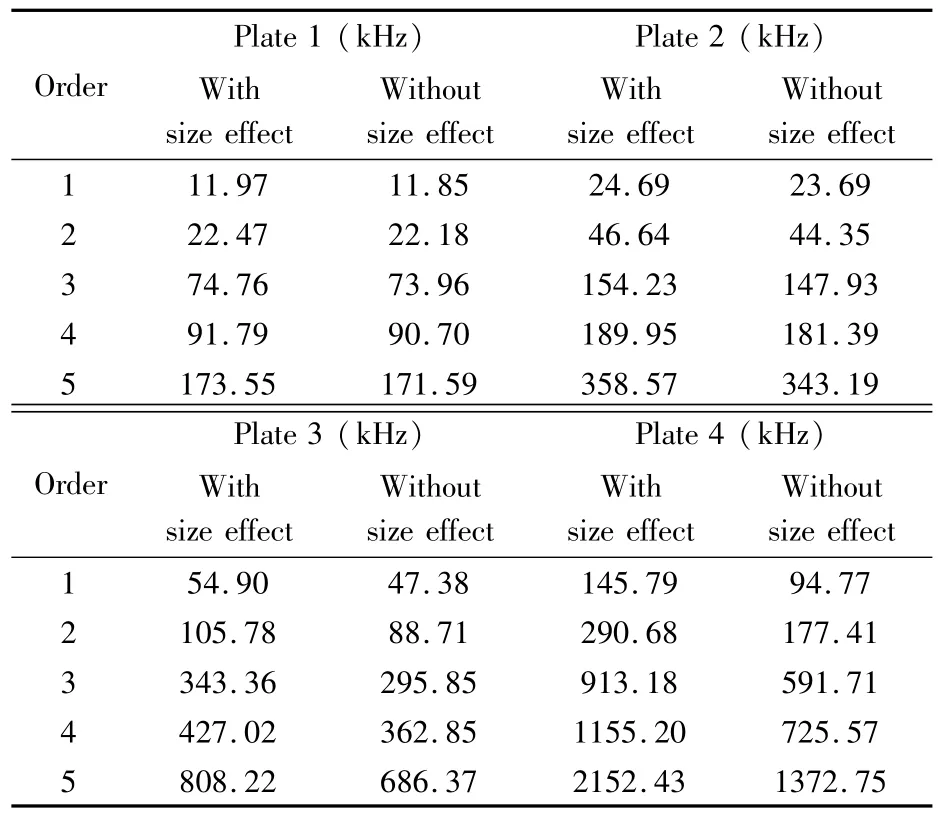
表3 固有频率计算结果Table 3 Numerical results of natural frequencies

以上结果也可用折线图的形式给出，可方便的观察各阶固有频率的变化规律.

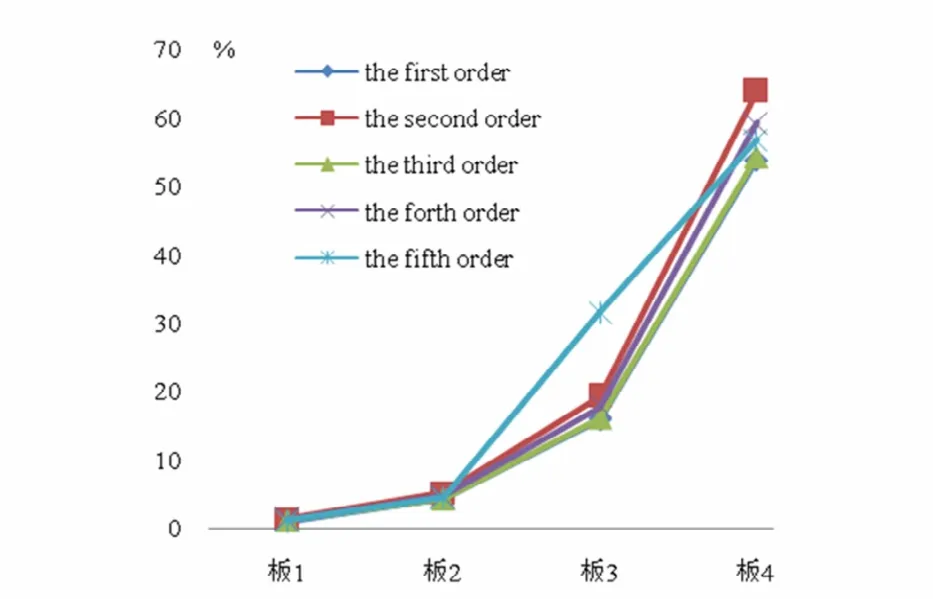
图5 考虑尺寸效应后各阶固有频率提升百分比Fig.5 Improvement percentage of natural frequencies considering the size effect

通过对比两种不同边界条件下的微型压电层合板结构的固有频率，可以发现尺寸效应对于微型压电四边简支板的固有频率提升效果要大于微型压电悬臂层合板.由于四边简支相对于悬臂是一种约束更强的边界条件，所以其本身的固有频率也更高，该结论说明当系统本身的固有频率较高时，尺寸效应对于固有频率的影响更加明显.

在得到微型压电悬臂板各阶固有频率后，通过Maple软件计算并绘制了振型函数图，如图6所示.

与微型压电四边简支板的计算结果类似，由微结构带来的尺度效应对结构刚度有提升效果，且该效果随着结构尺寸的减小愈发显著.

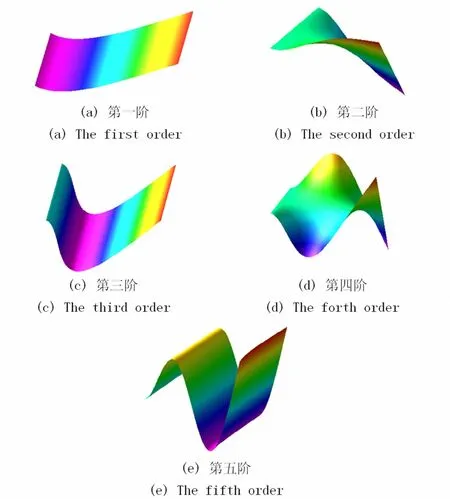
图6 前五阶模态图Fig.6 Mode shapes of the first five orders

为研究材料內凛长度l对固有频率的影响趋势，同样选取板3为研究对象，考察不同材料內凛长度l和板厚度的比值下的固有频率变化情况，结果如图7，单位kHz.

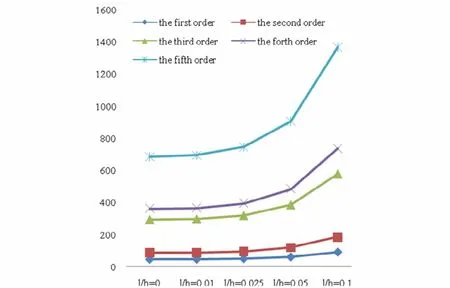
图7 各阶固有频率随l／h变化图Fig.7 Development of natural frequencies with differentl／h

通过计算发现随着材料內凛长度与板厚度的比值的增大，固有频率呈现出上升的趋势，该趋势表明尺寸效应的影响愈发明显.当材料內凛长度与板的厚度接近同一量级时，尺寸效应的影响已非常明显.

5 电压对于微型压电层合板固有频率的影响

因为压电材料也存在着逆压电效应，即在施加外电压时，压电材料本身也会产生应变.所以在外电压的影响下微型压电层合板的刚度也会发生改变.本节为考查电压对于微型压电层合板做自由振动时固有频率的影响，选取悬臂支撑条件下的板3为研究对象，考察施加不同外电压时系统的一二阶固有频率的变化的百分比.计算结果如图8.

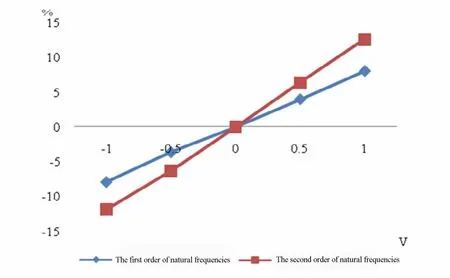
图8 固有频率随电压变化图Fig.8 Development of natural frequencies with different voltage

通过图8可看出随着外加电压由负到正的升高，固有频率呈现出上升的趋势，说明外加电压可以提升微型压电结构的刚度.且高阶固有频率的提升幅度更大.

6 对比和验证

为了验证本文所求得的动力学模型及求解的固有频率，下面选择四边简支的板3为对象，利用ANSYS软件进行了有限元模拟，ANSYS求得的前五阶固有频率如表4.

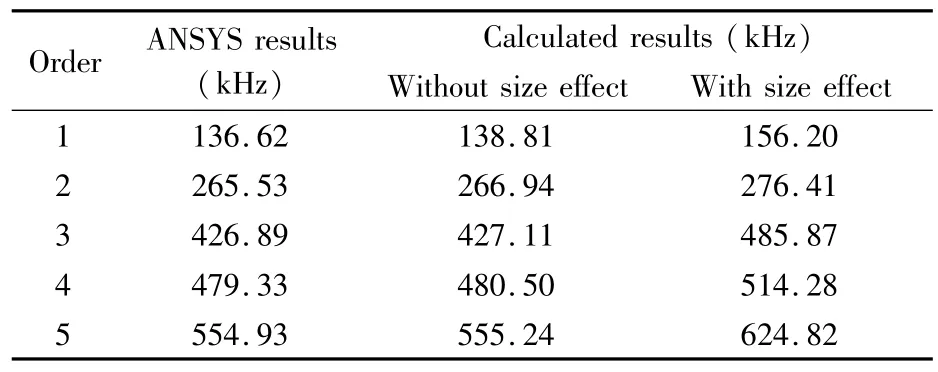
表4 固有频率验证Table 4 Verification of the natural frequencies

从表4可看出本文所求不考虑尺寸效应影响的固有频率与ANSYS所得出的结果相符.但当考虑尺寸效应的影响时两者的结果已有较大出入，说明在研究微结构的振动特性时ANSYS等有限元软件已不适合作为参考.

7 结论

针对微型压电层合板结构建立了模型，综合考虑压电效应和尺寸效应的影响，得到了动力学方程及其边界条件.并利用Ritz法分别对四边简支和悬臂支撑情况下的算例进行了振动特性分析.

通过分析发现结构尺寸在低于毫米量级之后，尺寸效应的影响开始变得显著，具体表现为结构尺寸的减小提高了系统的固有频率.随着结构尺寸的进一步减小，该趋势快速增大.而且尺寸效应对高阶固有频率的影响更加显著.与ANSYS软件有限元模拟结果的对比也表明了尺寸效应已不可忽略，传统理论也已不再适用，微结构的振动特性需要专门的微观力学理论来分析.

同时进一步研究发现材料內凛长度与板厚度的比值l／h是影响固有频率的重要参数，当该比值较小时，尺度效应的影响也较小.而当材料內凛长度与厚度两者接近同一量级时固有频率将出现非常大的提升.

通过对比两种不同边界条件下的微型压电层合板结构的固有频率，可以发现，尺寸效应对于四边简支板的固有频率提升效果要大于悬臂板.例如四边简支板的固有频率最大提升了87.3%，而悬臂板的固有频率最大提升了59.2%.由于四边简支相对于悬臂是一种约束更强的边界条件，所以其本身的固有频率也更高，该结论说明当系统本身的固有频率较高时，尺寸效应对于固有频率的影响更加明显.

最后，研究发现外加电压由负到正对于固有频率也有提升的作用，说明外加电压可以提升微型压电结构的刚度.且高阶固有频率的提升幅度更大.

1 FarisW，Nayfeh A H.Mechanical response of a capacitive microsensor under thermal load.Communications in Nonlinear Science and Numerical Simulation，2007，12（5）：776～783

2 Younis M I，Abdel-Rahman E M，Nayfeh A.A reducedorder model for electrically actuated microbeam-based MEMS.Journal of Microelectromechanical Systems，2003，12（5）：672～680

3 Fleck N A，Muller GM，Ashby M F，etal.Strain gradient plasticity：theory and experiment.Acta Metallurgicaet Materialia，1994，42（2）：475～487

4 Stölken J S，Evans A G.A microbend test method for measuring the plasticity length scale.Acta Materialia，1998，46（14）：5109～5115

5 Toupin R A.Elasticmaterialswith couple-stresses.Archive for Rational Mechanics and Analysis，1962，11（1）：385～414

6 Yang F，Chong A C M，Lam D C C，et al.Couple stress based strain gradient theory for elasticity.International Journal of Solids and Structures，2002，39（10）：2731～2743

7 Mindlin R D.Micro-structure in linear elasticity.Archive for Rational Mechanics and Analysis，1964，16（1）：51～78

8 Papargyri-Beskou S，Beskos D E.Static，stability and dynamic analysis of gradient elastic flexural Kirchhoff plates.Archive of Applied Mechanics，2008，78（8）：625～635

9 Lazopoulos K A.On bending of strain gradient elastic micro-plates.Mechanics Research Communications，2009，36（7）：777～783

10 Reddy J N.Microstructure-dependent couple stress theories of functionally graded beams.Journal of theMechanics and Physics of Solids，2011，59（11）：2382～2399

11 Ramezani S.A shear deformationmicro-platemodel based on themostgeneral form of strain gradient elasticity.International Journal of Mechanical Sciences，2012，57（1）：34～42

12 Rajabi F，Ramezani S.A nonlinear microbeam model based on strain gradient elasticity theory with surface energy.Archive of Applied Mechanics，2012，82（3）：363～376

13 Rajabi F，Ramezani S.A nonlinear microbeam model based on strain gradient elasticity theory.Acta Mechanica Solida Sinica，2013，26（1）：21～34

14 Park JC，Khym S，Park JY.Micro-fabricated lead zirconate titanate bent cantilever energy harvester withmulti-dimensional operation.Applied Physics Letters，2013，102（4）：043901

15 Defosseux M，Allain M，Defay E，et al.Highly efficient piezoelectric micro harvester for low level of acceleration fabricated with a CMOS compatible process.Sensors and Actuators A：Physical，2012，188：489～494

16 Andosca R，McDonald TG，Genova V，et al.Experimental and theoretical studies on MEMS piezoelectric vibrational energy harvesterswithmass loading.Sensors and Actuators A：Physical，2012，178：76～87

17 Ralib A A M，Nordin A N，Salleh H，etal.Fabrication of aluminium doped zinc oxide piezoelectric thin film on a silicon substrate for piezoelectric MEMS energy harvesters.Microsystem technologies，2012，18（11）：1761～1769

18 Pan C T，Liu Z H，Chen Y C，et al.Design and fabrication of flexible piezo-microgenerator by depositing ZnO thin films on PET substrates.Sensors and Actuators A：Physical，2010，159（1）：96～104

19 郭抗抗，曹树谦.压电发电悬臂梁的非线性动力学建模及响应分析.动力学与控制学报，2014（1）：18～23（Guo Kangkang，Cao Shuqian.Nonlinearmodeling and analysis of piezoelectic cantilever energy harvester.Journalof Dynamics and Control，2014（1）：18～23（in Chinese））

20 Hu Y，Wang J，Yang F，et al.The effects of first-order strain gradient in micro piezoelectric-bimorph power harvesters.Ultrasonics，Ferroelectrics，and Frequency Control，IEEE Transactions on，2011，58（4）：849～852

21 郑兆昌.机械振动.北京：机械工业出版社，1980（Zheng J C.Mechanical vibration.Beijing：China Machine Press，1980（in Chinese） ）

VIBRATION ANALYSISOFTHE M ICRO PIEZOELECTRIC LAM INATED PLATE BASED ON THE STRAIN GRADIENT THEORY*

Zhang Xiaozhi Chen Lihua†ZhangWei
（Beijing Key Laboratory of Nonlinear Vibrations and Strength of Mechanical Structures College of Mechanical Engineering，Beijing University of Technology，Beijing100124，China）

The dynamic model of the micro laminated plates is developed with its boundary conditions through Hamilton＇s principle，based on the classical thin plate theory and taken into consideration of the size effect caused by themicro scale using the strain gradient theory.After choosing the propermode functions for the boundary conditions of both simple-support and cantilever，the first five orders of natural frequencies and the corresponding 3D mode shapes are achieved by the Ritzmethod，respectively.The effect of size effect on natural frequencies is studied.Eventually，the influence of the external voltage on the natural frequency is also examined.

strain gradient theory， ritzmethod， vibration analysis， natural frequency， mode shape

10.6052／1672-6553-2015-79

2015-4-29收到第1稿，2015-6-11收到修改稿.

*国家自然科学基金资助项目（11472019）

†通讯作者E-mail：chenlihua＠bjut.edu.cn

Received 29 April 2015，revised 11 June 2015.

*The project Supported by the National Natural Science Foundation of China（11472019）

†Corresponding author E-mail：chenlihua＠bjut.edu.cn