考虑齿轮啮合激励的齿轮传动轴系扭振特性分析*

于姝雯 王东华 刘志刚 李玩幽

（哈尔滨工程大学，哈尔滨 150001）

考虑齿轮啮合激励的齿轮传动轴系扭振特性分析*

于姝雯 王东华 刘志刚 李玩幽†

（哈尔滨工程大学，哈尔滨 150001）

在传统齿轮传动轴系扭转振动计算中，将齿轮副简化为单一惯量而忽略齿轮啮合动态激励，会导致轴系扭转振动特性分析的结果不能正确描述轴系实际工作状态.本文以齿轮传动轴系为对象，考虑齿轮啮合的动态特性，建立轴系扭转振动当量模型.对齿轮啮合时变刚度和啮合激励力进行Matlab数值模拟.将Newmark逐步积分法应用于轴系扭转振动强迫振动响应的计算中，计算在齿轮啮合动态激励扭矩和外加负载扭矩的分别作用和共同作用下的轴系扭转振动响应情况，比较分析结果，说明了齿轮啮合动态特性是轴系扭转振动的重要激励源而不可忽视这一事实.

轴系扭转振动， 齿轮啮合时变刚度， 齿轮啮合动态激励， 强迫振动响应， 外部负载扭矩

引言

在船舶轴系中，齿轮增减速传动系统的应用十分广泛.根据船级社《钢制海船入级与建造规范》中的相关规定［1］，为保证轴系强度满足要求，需要计算轴系的扭转振动响应.在齿轮传动轴系的扭转振动计算时，不要求考虑齿轮副的啮合激励作用.

在柴油机等往复机械中，作用在轴系上的各气缸工作激励扭矩远大于齿轮啮合激励扭矩，此时，齿轮啮合激励扭矩对轴系扭转振动计算的影响可忽略.然而，在非往复设备的传动轴系扭转振动计算中，由于齿轮啮合激励扭矩是轴系扭转振动的重要激励源之一，将齿轮副简化为单一惯量的传统处理方式即忽略齿轮啮合动态激励，不能正确的反映轴系实际扭转振动状态.

众多研究者深入地研究了齿轮副的动力学特性，对本文齿轮副动力学数值模拟有着指导意义.Y.Cai［2］给出了齿轮啮合刚度的模拟公式，并已在实验基础上得到修正.对齿轮系统的非线性动力学微分方程线性化，并能对齿轮啮合激励进行数值模拟及基于有限元法的啮合刚度的模拟，实现对齿轮啮合接触的有限元分析［3-8］.响应分析多集中于齿轮箱体振动的有限元法分析［9-11］.齿轮啮合对称轴系会产生轴系扭转振动异向振动现象［12］.

为说明齿轮啮合对轴系扭转振动响应的影响情况，本文以齿轮传动轴系为研究对象，首先对齿轮啮合时变刚度、齿轮啮合动态激励进行Matlab数值模拟.对轴系进行集总参数简化，建立轴系扭转振动当量参数模型.依据Newmark逐步积分原理，进行系统扭转强迫振动响应计算.对在齿轮内部激励扭矩和外加负载波动扭矩，分别作用和共同作用下，轴系扭转振动响应进行计算与分析.

1 齿轮系统内部激励的数值模拟

1.1 齿轮副扭振模型

对齿轮副处进行细化建模，即齿轮副主从动轮简化成两个惯量，考虑齿轮啮合时变动态特性对轴系扭转振动的影响.齿轮副处扭转振动动力学模型［5］如图1所示.

齿轮传动系统振动微分方程为：

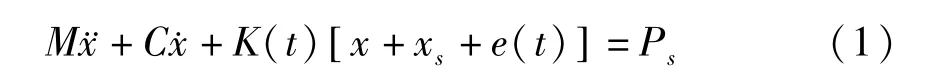
式中，M，C，K分别是质量、阻尼、刚度矩阵，其中刚度矩阵包含了齿轮结构刚度以及齿轮啮合的时变刚度.刚度的时变性使得振动微分方程的非线性.为了便于分析，将刚度的时变部分进行分离，并以激励的形式移到方程的右边，这样就使得非线性的振动微分方程线性化.改写过程为［5］：

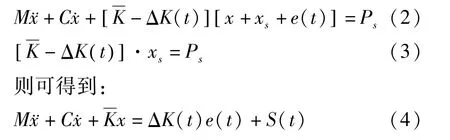
方程（4）的右边载荷部分即齿轮啮合动态激励的表达形式.

图1 齿轮副扭转振动分析模型Fig.1 The torsional vibration model of gear pair

采用的单级直齿圆柱齿轮相关参数见表1.

表1 齿轮副详细参数Table 1 Details of gear pair

1.2 齿轮啮合刚度数值模拟

依据Y.Cai公式［2］，用Matlab软件对齿轮啮合刚度进行数值模拟.数值模拟得到齿轮副单齿啮合时变刚度曲线如图2所示.

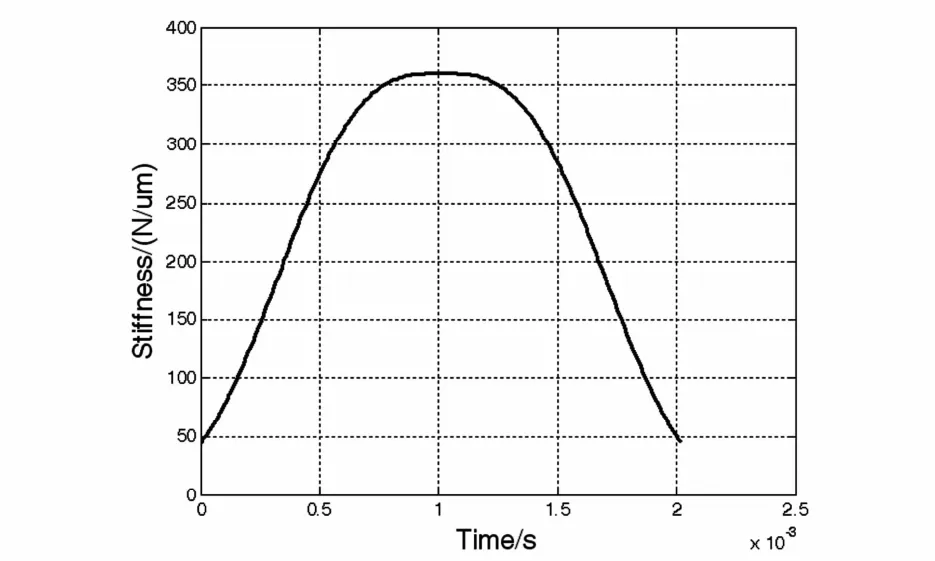
图2 单齿啮合刚度曲线Fig.2 The stiffness curve of single gear

直齿圆柱齿轮传动的重合度εα为：

经计算得齿轮啮合重合度为2.0231，齿轮副啮合周期为Tz＝εα×60／n＝0.002023s.据此对齿轮啮合刚度进行综合叠加，得到齿轮副综合啮合刚度（如图3所示）以及主动轮、从动轮扭转啮合刚度曲线如图4所示.主动齿轮扭转啮合刚度的平均值为1.86E6Nm／rad.

图3 齿轮综合啮合刚度曲线Fig.3 The stiffness curves of themesh gears

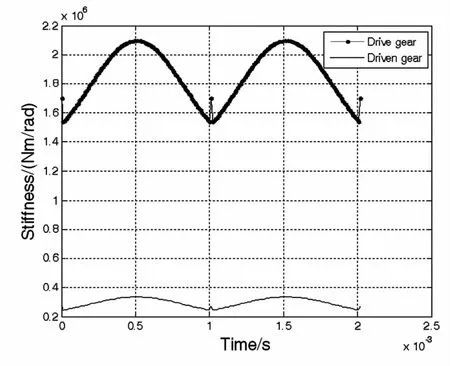
图4 齿轮扭振啮合刚度曲线Fig.4 The torisional stiffness curves of themesh gears

1.3 齿轮啮合误差激励的数值模拟

根据齿轮设计的精度等级确定齿轮的偏差，采用简谐函数表示法进行误差模拟［5］，则轮齿的齿形误差和基节误差可用正弦函数.具体表示为：

式中，Tz是齿轮的啮合周期，εα是重合度，n为输入转速，e0，er是齿轮误差幅值.对误差激励数值模拟结果如图5所示.

图5 齿轮传动误差曲线Fig.5 The error curve of themesh gears

1.4 齿轮啮合动态激励的合成

根据公式（4），将单齿啮合刚度曲线（图2）与误差曲线（图5）对应点相乘，合成为齿轮啮合内部激励［13］，如图6所示.将单齿激励进行综合，得到的齿轮综合激励曲线如图7所示.

图6 单齿激励合成曲线Fig.6 The excitation curve of the single gear

图7 齿轮综合激励曲线Fig.7 The excitation curve of themesh gears

将齿轮综合激励曲线中各时间点对应的激励值减去其中最小值，再将其转化到主动齿轮、被动齿轮径向方向的扭矩曲线，如图8、9所示.

图8 主动齿轮啮合动态激励扭矩曲线Fig.8 The torque curve of the drive gear

图9 从动齿轮啮合动态激励扭矩曲线Fig.9 The torque curve of the driven gear

2 轴系扭转振动当量模型

采用集总参数法对轴系进行当量简化，系统结构示意图如图10所示.建立轴系扭振振动分析模型，按照振动的特性不变的原则，将实际的轴系进行合理的简化.简化后的系统是由10个只有转动惯量而无弹性变形的集中质量和9个只有弹性变形而无转动惯量的一些弹性轴段组成［14］.

图10 系统结构简图Fig.10 The structure of the shaft system

按照简化原则对轴系简化的当量参数见表2.轴系当量模型见图如图11所示.

表2 轴系扭振当量参数Table 2 Torsional vibration parameters of shaft equivalentmodel

图11 轴系扭振当量模型Fig.11 The torsional equivalentmodel of the shaft system

3 轴系扭转振动自由振动计算

系统自由振动微分方程［15］为：

设方程的解的形式为：

则可以得到矩阵方程：

式中，K为扭转刚度矩阵，J为转动惯量矩阵，λ为系统矩阵特征值.并可得到系统固有频率为：

按照以上原理编制MATLAB计算程序，扭转自由振动前四阶固有频率见表3.

自由振动计算中的齿轮啮合刚度采用的是由Y.Cai公式近似计算的啮合刚度的平均值（1.86 E6Nm／rad）.考虑到啮合刚度的时变性，将齿轮啮合刚度依次取10～1E10Nm／rad，得到前三阶固有频率与齿轮啮合刚度的关系曲线.

表3 扭转振动固有频率Table 3 Natural frequency of torsional vibration

如图12所示，齿轮扭转振动啮合刚度低于1E4Nm／rad时，前三阶临界转速均有较大波动，啮合刚度大于1E5Nm／rad时，前四阶固有频率变化平稳.由图4可知，主动轮、从动轮扭转刚度范围大于1E5Nm／rad，因此，针对此系统，刚度时变性不会引起前四阶固有频率大范围的变化.

图12 扭转振动固有频率随齿轮啮合刚度变化曲线Fig.12 The torsional equivalentmodel of the shaft system

4 轴系扭转振动强迫振动响应计算

4.1 齿轮内部激励作用下的轴系扭振响应分析

将Newmark逐步积分法［16］应用于轴系扭转振动响应的分析中，计算流程如图13所示.

轴系强迫振动微分方程为：

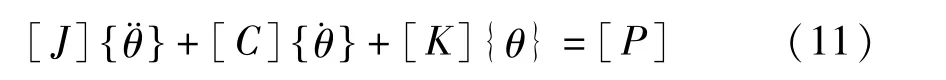
将齿轮啮合动态激励作为轴系唯一激振力，计算强迫振动响应.图14为惯量7的轴系扭转振动的角加速度响应时域曲线.将其进行傅里叶变换得到频域曲线如图15所示，图中明显的峰值频率为啮合频率（492.7Hz）及啮合频率的二倍频（985.4Hz）、四倍频（1970.8Hz）等.说明齿轮啮合动态激励引起了轴系较明显的扭转振动响应，对轴系扭转振动有一定的激振能力.

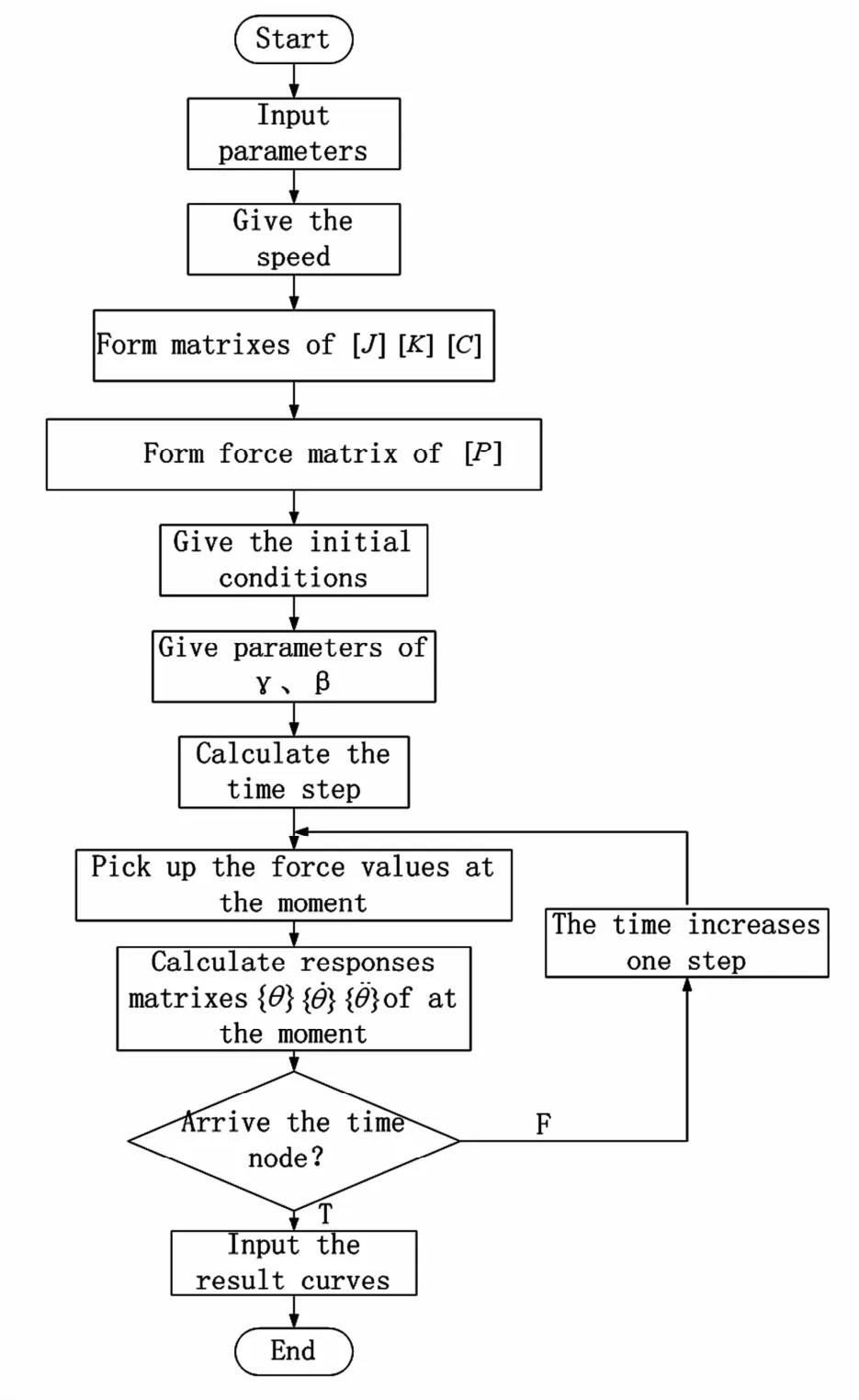
图13 Newmark法扭振计算流程图Fig.13 The flow chart of Newmark Method for torsional vibration calculation

图14 齿轮动态激励作用下惯量7角加速度响应时域曲线Fig.14 The time domain curve of the7th-inertia angular acceleration under the gearmesh torque

在齿轮啮合动态激励作用下各轴段的应力如图16所示，在轴段2（主动轮惯量与轴系的连接轴段）和轴段6（从动轮惯量与轴系的连接轴段）处应力最大.

图15 齿轮动态激励作用下惯量7角加速度响应频域曲线Fig.15 The frequency domain curve of the 7th-inertia angular acceleration under the gearmesh torque

图16 齿轮动态激励作用下轴段应力值Fig.16 The stress curve of each shaft section under the gearmesh torque

4.2 外加负载作用下轴系扭振响应计算与分析

本文研究对象的外加负载扭矩是通过发电机提供且施加在发电机惯量10上.发电机功率为8kW，齿轮箱输入转速1000r／min.负载扭矩幅值计算公式为负载扭矩以矩形波的形式施加，如图17所示，频率为1000Hz的波动负载扭矩曲线.

图17 外部负载扭矩曲线Fig.17 The torque curve of the external loading

4.2.1 不考虑齿轮啮合动态激励

不考虑齿轮啮合动态激励时，外部负载扭矩作为轴系扭转振动响应的唯一激振扭矩，计算轴系扭转振动响应，如图18、19所示，外部负载频率为1000Hz时，惯量7角加速度响应时域、频域曲线，频谱图中没有齿轮啮合激励频率及其倍频成分.轴段应力如图20所示，仍然是轴段2和轴段6处应力出现明显峰值.

图18 负载扭矩作用下惯量7角加速度响应时域曲线Fig.18 The time domain curve of the 7th-inertia angular acceleration under the external loading

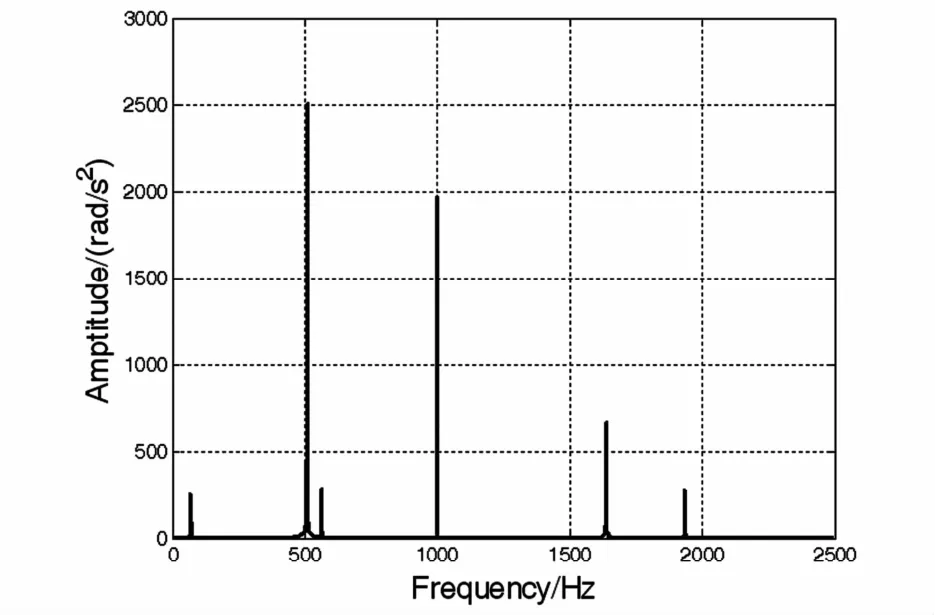
图19 负载扭矩作用下惯量7角加速度响应频域曲线Fig.19 The frequency domain curve of the 7th-inertia angular acceleration under the external loading

使负载扭矩频率在60～1000Hz范围内变化，步长取5Hz，分别计算各频率时的扭转振动响应，得到的轴段2、轴段6应力值随波动负载频率变化如图21、22所示.应力峰值频率为扭转振动固有频率（70Hz、290Hz、510Hz、565Hz），是由于负载扭矩频率与系统固有频率相等时，发生共振现象，响应剧烈.除此之外，在170Hz处还有一明显峰值，经分析，170Hz是扭振第一阶固有频率的2.5倍，齿轮副传动速比是2.5，齿轮副传动频率出按2.5谐次放大.因此实际工程中，也要十分注意这一现象.除了要避免系统固有频率外，还要注意齿轮传动比对第一阶固有频率倍频成分的放大作用.

图20 负载扭矩作用下轴段应力值Fig.20 The stress curve of each shaft section under the external loading

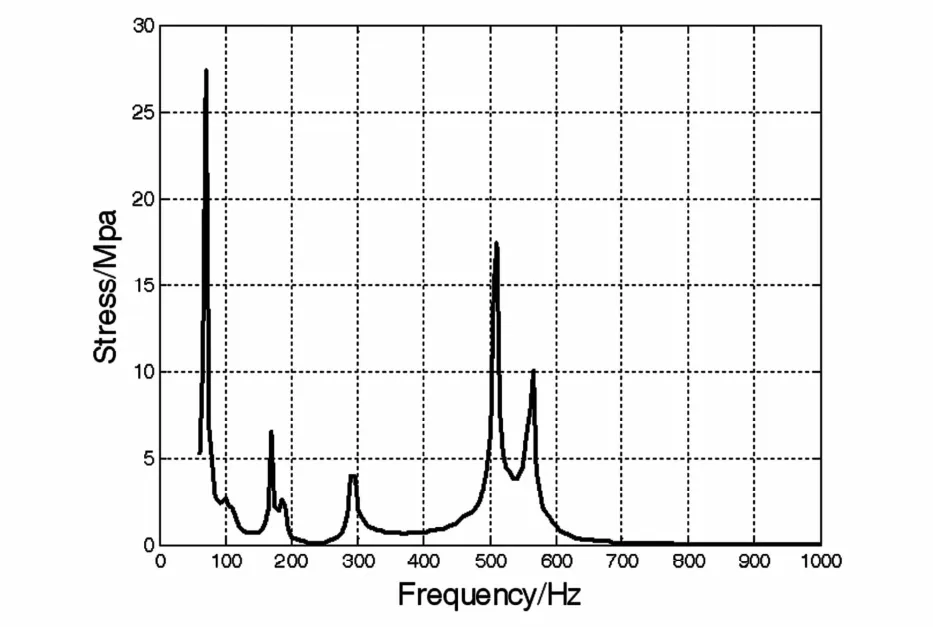
图21 负载扭矩作用下轴段2应力随负载频率变化曲线Fig.21 The stress curve of the second shaft section with the change of frequencies of external loading

图22 负载扭矩作用下轴段6应力随负载频率变化曲线Fig.22 The stress curve of the 6th shaft section with the change of frequencies of external loading

4.2.2 考虑齿轮啮合动态激励

轴系扭振响应的激振力矩同时考虑作用在主、从动齿轮上的齿轮啮合激励扭矩以及作用在发电机负载惯量上的负载扭矩，计算轴系扭振响应.图23、24为两激励扭矩共同作用、外部负载频率为1000Hz时，惯量7角加速度响应时域曲线及频域曲线.轴段应力曲线如图25所示.频域曲线中能体现齿轮啮合激励频率及其倍频成分.

图23 齿轮动态激励与负载扭矩共同作用下惯量7角加速度响应时域曲线Fig.23 The time domain curve of the 7th-inertia angular acceleration under the gearmesh torque and external loading

图24 齿轮动态激励与负载扭矩共同作用下惯量7角加速度响应频域曲线Fig.24 The frequency domain curve of the 7th-inertia angular acceleration under the gearmesh torque and external loading

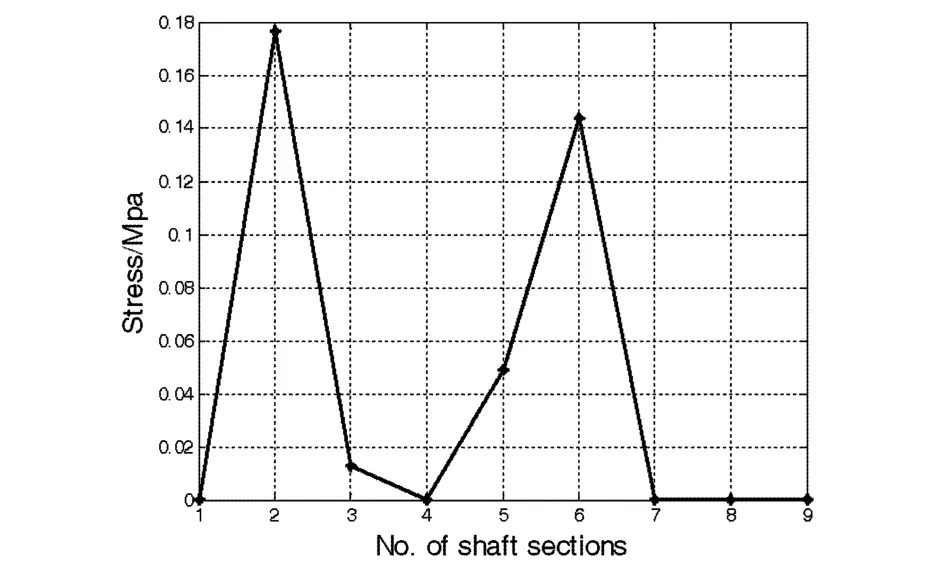
图25 齿轮动态激励与负载扭矩共同作用下轴段应力值Fig.25 The stress curve of each shaft section under the gearmesh torque and external loading

改变负载扭矩的频率，负载扭矩频率变化范围为60～1000Hz，变化步长取5Hz，分别计算扭振响应.得到的轴段2、轴段6应力值随波动负载频率变化曲线如图26、27所示.

图26 齿轮动态激励与负载扭矩共同作用下轴段2应力随波动负载频率变化曲线Fig.26 The stress curve of the second shaft section with the change of frequencies of external loading

图27 齿轮动态激励与负载扭矩共同作用下轴段6应力随波动负载频率变化曲线Fig.27 The stress curve of the 6th shaft section with the change of frequencies of external loading

5 结论

在非往复机械轴系的扭转振动计算时，传统的简化齿轮幅啮合结构为单一惯量的方式忽略了齿轮啮合动态激励对轴系扭转振动的作用.在电机驱动带有简单直齿轮的传动轴系工作时，恒转速电机运行平稳，外部激励可忽略，此时轴系仍有很大的振动噪声，这正是由于齿轮啮合动态特性的作用结果.本文基于Newmark逐步积分法，得到多组轴系扭转振动强迫振动响应结果.说明了齿轮啮合动态激励是轴系扭转振动的一个重要激励源而不可忽略.

由于齿轮啮合动态激励扭矩的作用，轴系扭转振动频谱中含有较大幅值的齿轮啮合激励频率及其二倍频、四倍频等.且轴段应力最大值均出现在主、从动轮惯量与轴系其他部件惯量的连接轴段.因此齿轮啮合动态激励对轴系扭转振动有明显的激振作用.若忽略齿轮啮合激励，扭转振动计算结果则不能完整描述轴系振动特性，齿轮啮合动态激励对轴系扭转振动的影响不能忽略.

齿轮传动作用放大了轴系扭转振动第一阶固有频率的某一倍频值，该倍频值等于齿轮副速比，在解决工程实际问题时，这一现象值得关注.

1 中国船级社，钢制海船入级与建造规范.北京：人民交通出版社，（CCS，Rules and regulations for the construction and classification of sea-going steel ships.Beijing：China Communications Press（in Chinese））

2 Cai Y.Simulation on the rotational vibration of helical gears in consideration of the tooth separation phenomenon（A new stiffness function of helical involutes tooth pair）.Journal of Mechanical Design，1995：460～469.

3 林腾蛟，李润方，朱才朝等.斜齿轮的齿面载荷及啮合刚度数值分析.机械工艺师，2000，10：30～31（Ling T J，Li R F，Zhou C Z，etal.Numerical analysis ofmeshing stiffness and tooth surface load of helical gear.Machinery Manufacturing Engineer，2000，10：30～31（in Chinese））

4 李润方，林腾蛟，陶泽光.齿轮系统耦合振动响应的预估.机械设计与研究，2003，19（2）：27～29（Li R F，Lin T J，Tao ZG.The response prediction of gear system coupled vibration.Machine Design and Research，2003，19（2）：27～29（in Chinese））

5 李润方，陶泽光，林腾蛟等.齿轮啮合内部动态激励数值模拟.机械传动，2001，25（2）：1～3（Li R F，Tao Z G，Lin T J.Numerical simulation for inner dynamic excitation of gearing.Mechanical Transmission，2001，25（2）：1～3（in Chinese））

6 龙凯，程颖.齿轮啮合力仿真计算的参数选取研究.计算机仿真，2002，19（6）：1～3（Long K，Cheng Y.The research of parameters by the simulation of exciting force in gears.Computer Simulation，2002，19（6）：1～3（in Chinese））

7 武宝林，杨素君，姚俊红.齿轮传动中啮合冲击的理论分析.机械科学与技术，2003，22（1）：55～57（Wu B L，Yang SJ，Yao JH.Theoretical analysis onmeshing impact of involute gears.Mechanical Science and Technology，2003，22（1）：55～57（in Chinese））

8 盛云，武宝林.齿轮传动中啮合冲击的计算分析.机械设计，2005，22（7）：41～43（Sheng Y，Wu B L.Calculation analysis onmeshing impact in gear transmission.Journal of Machine Design，2005，22（7）：41～43（in Chinese））

9 杨成云，林腾蛟，李润方等.增速箱动态激励下响应分析.重庆大学学报，2002，25（2）：15～18（Yang CY，Lin T J，Li R F，et al.Response analysis of speed increase gearbox system in dynamic excitation.Journal of Chongqing University（Natural Science Edition），2002，25（2）：15～18（in Chinese））

10 林腾蛟，蒋仁科等.船用齿轮箱动态响应及抗冲击性能数值分析.振动与冲击，2007，26（12）：14～17（Lin T J，Jiang R K，et al.Numerical simulation of dynamic response and shock resistance ofmarine gearbox.Journal of Vibration and Shock，2007，26（12）：14～17（in Chinese））

11 李慧新，吕杏梅，王靛等.弹性支撑下风电机组传动系统结构动力分析.动力学与控制学报，2015，13（4）：293～299（Li H X，Lv X M，Wang D，et al.Analysis of mounting on drive train structural dynamical specialty of a wind turbine.Journal of Dynamic and Control，2015，13（4）：293～299（in Chinese））

12 袁兴军.含有对称分支结构轴系异向振动特性研究［博士学位论文］.哈尔滨：哈尔滨工程大学，2010（Yuan X J.Investigation of reverse vibration characteristics of shaft with symmetrical embranchment［PhD Thesis］.Harbin：Harbin Engineering University，2010（in Chinese））

13 刘文.齿轮系统结构噪声及空气噪声分析与试验研究［博士学位论文］.重庆：重庆大学，2010（Liu W.Numerical analysis and experiment study on structural-borne noise and air-borne noise of gear system［PhD Thesis］.Chongqing：Chongqing University，2010（in Chinese））

14 陈之炎.船舶推进轴系振动.上海：上海交大出版社，1987：7～33，60～120（Chen Z Y.Ship propulsion shafting vibration.Shanghai：Shanghai Jiaotong University，1987：7～33，60～120（in Chinese））

15 王祺.内燃机轴系扭转振动.辽宁：大连理工大学出版社，1991：48～53（Wang Q.The torsional vibration of the internal combustion engine.Liaoning：Dalian University of Technology Press，1991：48～53（in Chinese））

16 张志华.动力装置振动数值计算.哈尔滨：哈尔滨工程大学出版社，1994：77～81（Zhang Z H.Numerical calculation of vibration of power unit.Harbin：Harbin Engi-neering University Press，1994：77～81（in Chinese） ）

ANALYSISOF GEAR SHAFTING TORSIONAL VIBRATION CHARACTERISTICS CONSIDERING THE MESHING GEARS INCENTIVES*

Yu Shuwen Wang Donghua Liu Zhigang LiWanyou†
（Harbin Engineering University，Heilongjiang，Harbin150001，China）

Taking a gear-driving shaft system as the object in this paper，an equivalentmodel of the target system with shafting torsional vibration is developed.At first，the free vibration analysis is studied to obtain the natural frequencies of the torsional vibration.Then，the gear variable stiffness and the gear dynamic excitation are simulated by the software Matlab.Moreover，the Newmark Step Integration Method is applied to calculate the forced vibration response of the shaft torsional vibration under gear dynamic excitation or extra-applied load torque or both.It is concluded from the comparison of the results that gear dynamic excitation cannotbe neglected in the shafting torsional vibration.

shafting torsional vibration， gear variable stiffness， gear dynamic excitation， forced vibration response， extra-applied load torque

10.6052／1672-6553-2015-87

2015-10-29收到第1稿，2015-11-2收到修改稿.

*国家自然科学基金资助项目（51375104）

†通讯作者E-mail：253352615＠qq.com

Received 29 October 2015，revised 2 November 2015.

*The project supported by the National Natural Science Foundation of China（51375104）

†Corresponding author E-mail：253352615＠qq.com