简化Lorenz系统多翅膀混沌吸引子的设计与电路实现*

孙克辉傅元理

（1.中南大学物理与电子学院，长沙 410083）（2.新疆大学物理科学与技术学院，乌鲁木齐 830046）

简化Lorenz系统多翅膀混沌吸引子的设计与电路实现*

孙克辉1，2†傅元理1

（1.中南大学物理与电子学院，长沙 410083）（2.新疆大学物理科学与技术学院，乌鲁木齐 830046）

基于简化Lorenz系统，通过设计非线性函数，得到单方向多翅膀混沌吸引子.在此基础上，通过引入切换控制函数，得到了网格多翅膀混沌吸引子.通过相图、耗散性、平衡点、分岔图和Poincaré截面方法，分析了系统的动力学特性.结果表明，该多翅膀系统具有丰富的动力学行为.设计并实现了网格多翅膀系统的模拟电路，通过示波器观测到网格多翅膀混沌吸引子，验证了该系统的物理可实现性，电路实验结果与数值仿真结果相一致.

混沌， 网格多翅膀吸引子， 简化Lorenz系统， 非线性函数，电路实现

引言

1963年Lorenz提出了Lorenz系统［1］，掀起混沌研究的热潮.1984年，蔡少棠教授提出能产生双涡卷的蔡氏电路［2］，首次在混沌理论和非线性电路之间架起了桥梁.混沌在保密通信、系统控制等领域具有广泛的应用前景.为了将混沌更好的应用于保密通信，人们长期致力于研究结构更复杂、性能更优的混沌系统，既强化混沌系统［3-6］.多翅膀混沌系统由于具有更复杂的动力学行为，成为混沌领域的研究热点之一.

经典的Lorenz混沌系统其吸引子的拓扑结构与蝴蝶的形状十分相似，被称为双翅膀混沌系统.类似的还有Lü系统［7］，Chen系统［8］，统一混沌系统［9］等.如何基于双翅膀混沌系统设计出多翅膀混沌吸引子一直是众多研究者的研究课题.一类多翅膀吸引子是通过计算机仿真偶然得到的［10-12］.另外，文献［13］报道了环状多翅膀吸引子的研究成果，但都没有形成系统的方法，不具有普适性.另一类主要是采用与构造多涡卷混沌吸引子相同的思想，即在系统中引入合适函数，扩展指标为2的鞍焦平衡点.文献［14-15］在部分广义Lorenz系统中实现了数量可控的单方向2N多翅膀吸引子.文献［16-17］报道了在单方向多翅膀吸引子的基础上，在另一方向引入非线性函数生成N×M网格状多翅膀吸引子，但总的来说这类系统数量有限，设计新的网格多翅膀混沌系统仍然是个富有挑战性的课题.文献［18］提出了简化Lorenz系统，该系统只含有单参数，却有三参数经典Lorenz系统的性质.但是到目前为止，还没有关于简化Lorenz系统的多翅膀吸引子的研究报道.

本文以简化Lorenz系统模型为基础，研究了多翅膀混沌系统的设计与电路实现问题.首先在x轴引入偶对称分段非线性函数替代原方程中的交叉乘积项，使系统翅膀数在x方向上延伸，然后在z轴方向引入切换控制器，使系统吸引子在z轴方向延伸，生成了网格状多翅膀吸引子；并对系统进行了耗散性、平衡点分布、分岔图和Poincaré截面等分析；最后设计了相应的模拟电路，并进行电路实验.

1 简化Lorenz多翅膀混沌吸引子模型

1.1 简化Lorenz系统模型

单参数简化Lorenz系统的数学模型为［18］其中，x、y、z为系统状态变量，c是系统参数.图1为c＝1时的吸引子相图及系统随参数c变化的分岔图，可见，系统通过倍周期分岔进入混沌态，拥有多个周期窗口，且具有双翅膀状吸引子.

图1 简化Lorenz系统的相图和分岔图（a）c＝1时的吸引子x-z相平面图（b）系统随参数c变化的分岔图Fig.1 Phase diagram and bifurcation diagram of simplified Lorenz system（a）Phase diagram of attractor inx-zplane forc＝1（b）Bifurcation diagram（cis varying）

1.2 单方向多翅膀混沌吸引子的设计

多翅膀混沌吸引子的设计原理为拓展指标2鞍焦点的个数，每个指标2的鞍焦点对应于一个翅膀吸引子.为了得到简化Lorenz多翅膀混沌吸引子，在简化Lorenz系统的基础上，引入偶对称分段非线性函数替代原系统中的交叉乘积项，且考虑到电路设计与实现需要，使系统变量范围在电子元器件动态范围之内，对系统变量进行等比例压缩.比例压缩系数p＝0.05，则系统方程变为

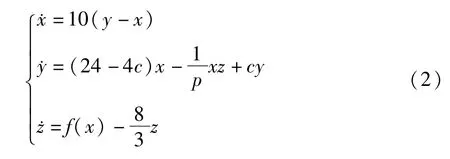
其中f（x）为偶对称分段非线性函数，由一个平方函数和偶对称的阶梯波序列组合而成，表达式为

其中F0、Fi、Ei为可调参数，共同控制非线性函数各段的斜率、幅度和宽度.图2为当参数选择如表1时的非线性函数f（x）的图形，可见，系统关于x＝0对称.令c＝1，N＝1、N＝2、N＝3、N＝4，以（0.1，0.1，0.1）为初始值进行仿真，可得系统的吸引子相图如图3所示.与图1（a）对比可知，在x方向引入偶对称分段非线性函数之后，系统从两翅膀混沌吸引子拓展成了多翅膀混沌吸引子.

图2 N＝4时参数可调多分段非线性函数f（x）Fig.2 Non-linearmulti-segment functionf（x）forN＝4

表1 可调参数Fi、Ei的取值Table 1 Values ofFiandEi

图3 单方向多翅膀混沌吸引子相图（a）N＝1，4翅膀；（b）N＝2，6翅膀（c）N＝3，8翅膀；（d）N＝4，10翅膀Fig.3 Phase diagram ofN-wing chaotic attractor（a）N＝1，4-wing attractor；（b）N＝2，6-wing attractor（c）N＝3，8-wing attractor；（d）N＝4，10-wing attractor

1.3 网格多翅膀混沌吸引子的设计

为了能得到网格多翅膀混沌吸引子，在系统（2）的基础上，在z方向上引入切换控制器g（z），得到网格多翅膀系统方程为

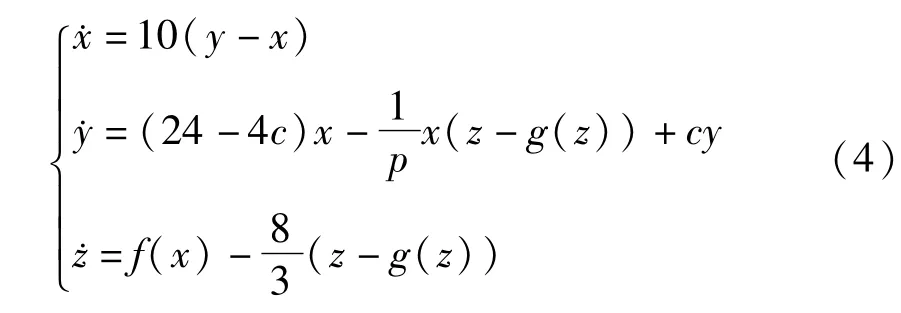
其中f（x）是偶对称分段非线性函数，其定义由式（3）给出.切换控制器g（z）的定义为

其中G与单方向多翅膀吸引子在z方向的跨度相关，zi为切换控制点.这样，系统（4）可产生（2N+2）×（M+1）网格状多翅膀混沌吸引子.若令M＝3，g（z）＝1.3［1+sgn（z-2.8）］-1.3［1-sgn（z-0.1）］-1.3［1-sgn（z+2.5）］，则切换控制器函数图形如图4所示.令c＝1，N＝2，M＝1；N＝2，M＝2；N＝2，M＝3；N＝4，M＝1；N＝4，M＝2；N＝4，M＝3时，可分别产生6×2，6×3，6×4；10×2，10 ×3，10×4网格多翅膀混沌吸引子.其数值仿真结果如图5所示.

图4 切换控制函数波形图Fig.4 Curve of the switch control function

图5 网格状多翅膀混沌吸引子（a）2×6翅膀吸引子；（b）2×10翅膀吸引子；（c）3×6翅膀吸引子；（d）3×10翅膀吸引子；（e）4×6翅膀吸引子；（f）4×10翅膀吸引子Fig.5 Phase diagram of grid multi-wing chaotic attractor（a）2×6-wing attractor；（b）2×10-wing attractor；（c）3×6-wing attractor；（d）3×10-wing attractor；（e）4×6-wing attractor；（f）4×10-wing attractor

2 网格多翅膀混沌系统的性能分析

单方向多翅膀混沌系统可以看成是网格多翅膀混沌系统中g（z）＝0的一个特例.因此，以网格多翅膀混沌系统为例，分析多翅膀混沌系统的动力学特性，包括c＝1时系统（4）的耗散性、平衡点分布、系统随控制参数c改变时的分岔图和Poincaré截面.

2.1 耗散性分析

由耗散性定义可得

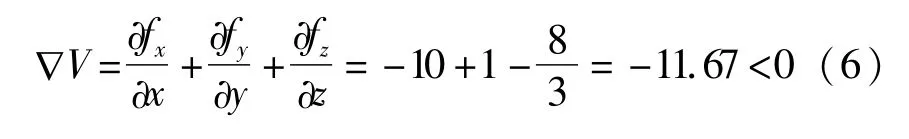
可见系统（4）是耗散的.意味着当t→∞时，所有的系统轨迹都会被限制在体积为零的集合上，其演化轨迹将表现为奇异吸引子.

2.2 平衡点及其稳定性分析

由式（7）求得的平衡点Q0（0，0，0）、Qi（u，u，w）.其中u，w由下式确定

根据前面给出的相关参数及式（8），令N＝4，M＝3，可得到4×10翅膀混沌吸引子的平衡点Qi（u，u，w）取值如式（9）所示.图6给出了其在x-z相平面上的40个平衡点分布.可见，通过引入偶对称分段非线性函数f（x），以及切换控制器g（z），系统原有的两个鞍焦平衡点已被扩展为（2N+2）×（M+1）个.

将系统（4）在平衡点Qi（u，u，w）处做线性化处理，得到平衡点Qi（u，u，w）处的雅克比矩阵为

其中F*（x）、G*（z）分别为f（x）、g（z）在对应平衡点处的导数值.为分析各个平衡点的类型，计算每个平衡点所对应雅克比矩阵的特征值，相关结果如下：

图6中用“°”标明的40个平衡点为指标2的鞍焦平衡点，根据多翅膀吸引子构造原理，每个指标2鞍焦点产生一个翅膀吸引子，可见系统能得到40个翅膀吸引子.

图6 x-z平面平衡点分布示意图Fig.6 Distribution of equilibrium points inx-zphase plane whenN＝4 andM＝3

2.3 分岔分析

当p＝0.05，N＝4，M＝3时，系统（4）的分岔图如图7所示.将图7（a）方框区域放大得到图7（b）.与原系统分岔图图（1b）对比可知，图7（b）几乎与图（1b）相一致，显然，新构造的网格多翅膀混沌系统较原系统具有更加复杂的动力学行为.

图7 4×10网格多翅膀系统分岔图（a）当c∈［-12，8］时的分岔图（b）当c∈［4.5，7.5］时的分岔图Fig.7 Bifurcation diagrams of4×10-wing system（a）Bifurcation diagram whenc∈［-12，8］（b）Bifurcation diagram whenc∈［4.5，7.5］

2.4 Poincaré截面

计算以y＝0为截面的4×10网格多翅膀混沌系统的Poincaré截面，结果如图8所示.可见，Poincaré截面上的点主要分布为4排，且清晰表示出每排所拓展出的翅膀形状，与吸引子相图图5（f）相一致，同时也验证了网格多翅膀系统处于混沌状态.

图8 4×10网格多翅膀混沌系统Poincaré截面Fig.8 Poincarésection of the 4×10-wing chaotic system

3 电路实现及实验结果

对网格多翅膀混沌系统（4）进行模拟电路的物理实现.以N＝2，M＝1为例设计其模拟电路，电路由两部分构成：第一部分为c＝1时简化Lorenz系统主体电路，如图9所示.当S1、S2打开时电路产生单方向6翅膀吸引子，当S1、S2闭合时电路产生6×2网格多翅膀.第二部分为偶对称多分段非线性函数f（x）和切换控制函数g（z）的产生电路，如图10所示.

根据图9和图10的电路图可得到非线性系统电路方程为

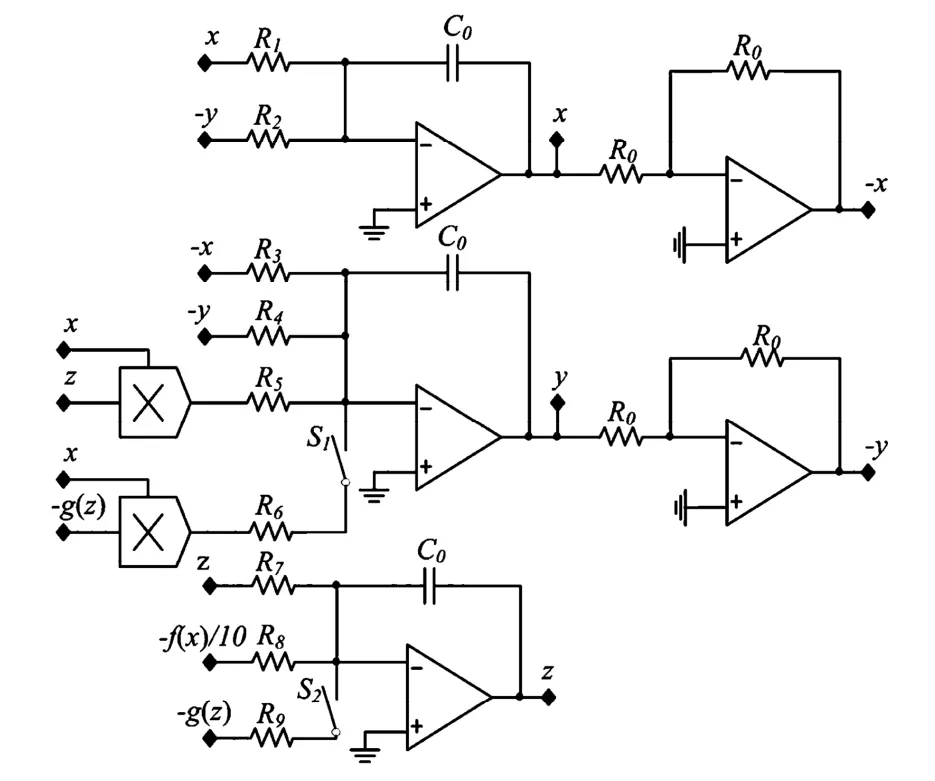
图9 网格多翅膀混沌系统主体电路Fig.9 Main circuit of grid multi-wing chaotic system

图10 N＝2、M＝1非线性函数电路（a）f（x）电路图；（b）g（z）电路图Fig.10 Circuit of non-linear function withN＝2，M＝1（a）Circuit realization off（x）；（b）Circuit realization ofg（z）

对比方程（12）和（4）得到R0＝R3＝10kΩ，C0＝1nF，R1＝R2＝R8＝100kΩ，R4＝1000kΩ，R5＝R6＝5kΩ、R7＝R9＝375kΩ.电路实现中用到了5%精度的线性电阻、线性电容、模拟乘法器和运算放大器.其中模拟乘法器采用的是AD633芯片，增益系数为0.1.运算放大器采用TL082，电源供电电压为± 15V，此时运算放大器的动态范围是±13.5V.图11为电路实验结果，可见实验结果与数值仿真结果相一致.表明电路设计正确，系统具有物理可实现性.

图11 电路实验相图（a）单方向4翅膀；（b）单方向6翅膀；（c）网格2×4翅膀；（d）网格2×6翅膀Fig.11 Results of circuit experimental（a）4-wing attractor；（b）6-wing attractor；（c）2×4-wing attractor；（d）2×6-wing attractor

4 结论

采用理论分析、数值仿真及电路实现的方法，研究了基于简化Lorenz系统的网格多翅膀混沌吸引子设计问题.通过在x方向引入偶对称多分段非线性函数及在z方向进行切换控制，拓展了系统指标为2的鞍焦平衡点，得到了网格多翅膀混沌吸引子.网格多翅膀混沌系统有更加复杂的动力学行为.最后设计并实现了该系统的模拟电路，验证了该系统的物理可实现性，多翅膀系统的应用将是我们下一步研究的课题.

1 Lorenz E N.Deterministic non-periodic flows.Journal of the Atmospheric Sciences，1963，20（3）：130～141

2 Chua L O，Komuro M，Matsumoto T.The double scroll family.IEEE Transactions on Circuits and Systems，1986，33（11）：1072～1118

3 孙克辉，艾星星，左婷.多涡卷Chua混沌吸引子的设计与性能分析.动力学与控制学报，2015，13（1）：11～17（Sun K H，Ai X X，Zuo T，et al.Design of Chua multi-scroll chaotic attrator and its performance analysis.Journal of Dynamics＆Control，2015，13（1）：11～17（in Chinese））

4 Zhang C X，Yu SM.Generation ofmulti-wing chaotic attractor in fractional order system.Chaos Solitons＆Fractals，2011，44（10）：845～850

5 Sun K H，Wang Y，Wang Y L.Hyperchaos behaviors and chaos synchronization of two unidirectional coupled simplified Lorenz systems.Journal of Central South University，2014，21（3）：948～955

6 艾星星，孙克辉，贺少波.不同类型混沌吸引子的复合.物理学报，2014，63（4）：040503（Ai X X，Sun K H，He S B.Compound attractors between different chaotic systems.Acta Physica Sinica，2014，63（4）：40503～040503（in Chinese））

7 LüJH，Chen G R.A new chaotic attractor coined.International Journal of Bifurcation＆Chaos，2002，12（3）：659～661

8 Chen GR，Ueta T.Yetanother chaotic attractor.International Journal of Bifurcation and Chaos，1999，9（7）：1465～1466

9 LüJH，Chen G R，Zhang S.Dynamical analysis of a new chaotic attractor.International Journal of Bifurcation＆Chaos，2002，12（5）：1001～1015

10王繁珍，齐国元，陈增强.一个四翼混沌吸引子.物理学报，2007，56（6）：3137～3144（Wang F Z，Qi G Y，Chen Z Q，et al.A four-winged chaotic attractor.Acta Phys Sinica，2007，56（6）：3137～3144（in Chinese））

11 Li Y X，Cao Y C，Huang X.A new 4D four-wing hyperchaotic attractor and its circuit implementation.IEEE Communications，Circuits and Systems（ICCCAS），2010：742～746

12 Giuseppe G.Novel four-wing and eight-wing attractors using coupled chaotic Lorenz systems.Chinese Physics B，2008，17（9）：3247-3251

13 Yu SM，LüJH，Tang K S，et al.A general muli-scroll Lorenz system family and its realization via digital signal processors.Chaos，2006，16（3）：033126（1～10）

14 Yu SM，Wallace K S，LüJH，et al.Generating 2n-wing attractors from Lorenz-like systems.International Journal of Bifurcation and Chaos，2010，38（3）：243～258

15 Bao BC，Wang X F，Xu JP.Multi-wing butterfly attractors in Lüsystem.2010 InternationalWorkshop on Chaos-Fractal Theory and its applications，2010，211～215

16 周欣，王春华，郭小蓉.一个新的网格多翅膀混沌系统及其电路实现.物理学报，2012，61（20）：200506（Zhou X，Wang C H，Guo X R.A new grid multi-wing chaotic system and its circuit implementation.Acta Physica Sinica，2012，61（20）：200506～379（in Chinese））

17 Yu SM，Zhang C X.On constructing complex grid multiwing hyperchaotic system：Theoretical design and circuit implementation.International Journal of Circuit Theory and Applications，2013，41（3）：221～237

18 Sun K H，Sprott JC.Dynamics of a simplified Lorenz system.International Journal of Bifurcation and Chaos，2009， 19（4）：1357～1366

DESIGN AND CIRCUIT IMPLEMENTATION OF THE SIMPLIFIED LORENZ MULTI-W ING CHAOTIC ATTRACTOR*

Sun Kehui1，2†Fu Yuanli1
（1.School of Physics and Electronics，Central South University，Changsha410083，China）
（2.School of Physics Science and Technology，Xinjiang University，Urumqi830046，China）

N-wing attractorswere first obtained by introducing a nonlinear function on the simplified Lorenz system in this paper.The gridmulti-wing attractorswere then realized through switching the control function in the z direction.Moreover，the dynamical characteristics of the Lorenz system were studied by the attractor phase diagram，dissipation，equilibrium points，bifurcation diagram and Poincarésection.The results show that the simplified Lorenz system exhibited a rich dynamical behaviors.Finally，the analog circuitof the system was designed and developed.The grid multi-wing attractors were observed through the oscilloscope，and the physical implementation of chaotic circuitwas verified.It is found that the results of circuit experimentand numerical simulation were accordant.

chaos， grid multi-wing attractor， simplified Lorenz system， nonlinear function， circuit implementation

10.6052／1672-6553-2015-85

2015-10-12收到第1稿，2015-11-13收到修改稿.

*国家自然科学基金资助项目（61161006，61573383）

†通讯作者E-mail：kehui＠csu.edu.cn

Received 12 October 2015，revised 13 November 2015.

*The project supported by the National Natural Science Foundation of China（61161006、61573383）

†Corresponding author E-mail：kehui＠csu.edu.cn